UNIT 4
Introduction to Beams
Types of Support
- Roller Support: -
Roller support is show in two ways as shown:
A free body diagram of roller support is shown in figure given below
- Roller support offers only one reaction; which is always perpendicular to the base or plane of roller.
- All the steel trusses of the bridges have one of their ends supported on roller.
- Main advantages of the support are that beam can easily move towards left or right due to expansion & contraction.
2. Hinge support
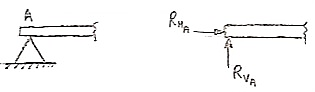
- In this case, end of the beam is hinged to the support as shown in figure above.
- This type of support offers two reactions, one is parallel to base and perpendicular to the base
- All the steel trusses of the bridges have one of their end roller supported & other end is hinged
- Main advantage of this support is that beam remains stable.
- If both ends of the beam are roller supported, then beam can not be stable. Thus, one support of beam is made roller supported and other is hinged.
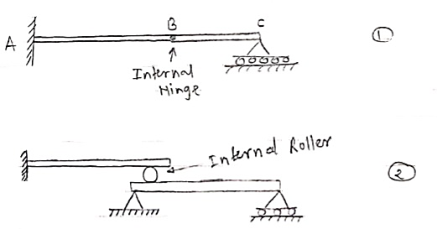
3. Internal Hinge: -
When two members are connected by the hinge then this type of support is called as internal Hinge.
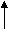
Internal Hinge Reactions at internal Hinge
Fixed support: -
Fixed support offers three reactions as shown in figure below.
- Reaction in horizontal direction.
- Reaction in vertical direction.
- Moment (fixing moment)
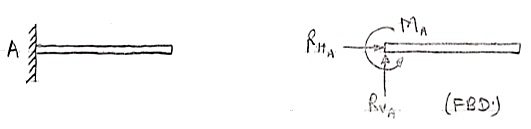
Fixed Support
Beam –
It is horizontal structural member on which different types of loads can be supported. It takes load from floor or roof & transfers to column.
The beam may be sometimes constructed in the inclined position for architectural point of view.
Types of Beam: -
- Simply supported beam –
A beam which is just resting on the supports at the end without any connection is known as simply supported beam. It is generally used for vertical landing system.
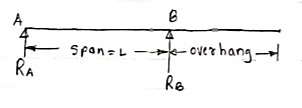
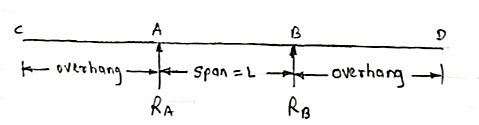
2. Overhanging Beam –
A beam which is supported at the intermediate point other than ends is called as overhanging beam. Here portion of beam is extended beyond the support
a)
(singly overhanging beam)
b)
(doubly overhanging beam)
3. Cantilever Beam –
A beam which is fixed at one end is called as cantilever beam
Here, there are three reactions components:
- Vertical reaction at A (RVA)
- Horizontal reaction at A (RHA)
- Fixing moment at A (MA)
We can assume any direction for above components.
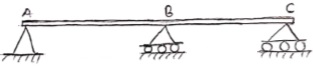
4. Continuous Beam:
A beam having more than two support is called as continuous beam.
5. Compound Beam:
When two or more beams are joined together by using internal hinge; or when one beam rests over another beam by using internal roller, then such beam is called as compound beam.
Type of Loads
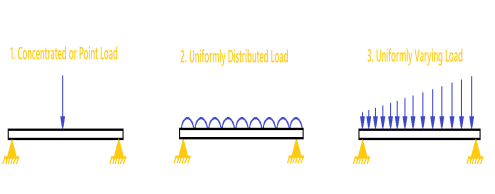
A beam is usually horizontal, and the applied load is vertical. Following are the different types of loads.
- Concentrated or Point Load: Act at a point.
- Uniformly Distributed Load: Load spread along the length of the Beam.
- Uniformly Varying Load: Load spread along the length of the Beam, Rate of varying loading point to point.
Sign conversion for Shear force and Bending moment
For a simply supported beam, If a point load is acting at the centre of the beam. Imagine a section X-X divide the beam into two portions. See the pic below.
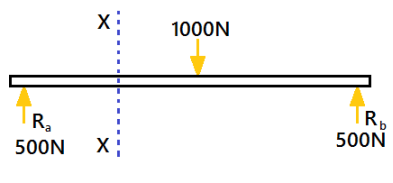
A simply supported beam is carrying a load (point load) of 1000N at its middle point. The reactions support will be equal to 500N(Ra=Rb). The section X-X make the beam into two parts.
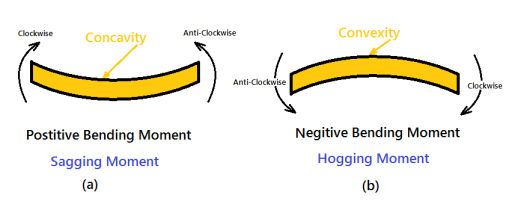
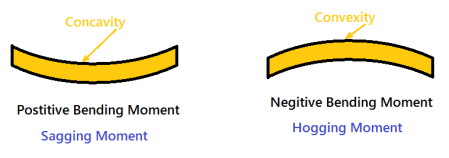
The moment of all the forces, i.e., load and reaction to the left of section X-X is Clockwise .The moment of all the forces, i.e., load and reaction to the right of section X-X are Anti-Clockwise.
So this makes the beam a Sagging moment(Concavity). Here the bending moment is Positive. See (a). If the left portion makes an anticlockwise moment and the right portion of the section makes a Clockwise moment, then it is hogging moment. Bending moment Negative.
Similarly for Shear force is positive when the left portion of the section goes upwards or the right portion of the section goes downwards.
Shear force is Negative when the left portion of the section goes downwards, or the right portion of the section goes upwards.
- Point load
Load acting at a single point on the beam is known as point load. Its unit is N or kN
2. Uniformly Distributed load (UDL) or Rectangular Load:
A load which is spread over the beam or part of the beam uniformly is known as UDL
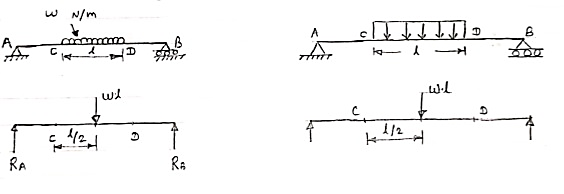
Conversion of UDL or Rectangular load into point load
= Intensity of UDL × distance
= w. l. ------------- N
3. Uniformly varying load or Triangular load:
A load whose intensity is linearly varying between the two points on the beam is known as UVL. If an intensity of the load at one end is zero and at other ends is maximum then it is called as uniformly varying load or triangular load.
Following figures shows different types of UVL
- To convert UVL into point load, calculate the area of uniformly varying load.
- For location of point load find x coordinate of centroid of the UVL area.
3.
Question 1). Find the support reactions of given beam for loading as shown below.
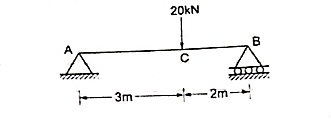
Answer 1)
Draw FBD of given beam & applying conditions of equilibrium
∑fx = 0
RHA = 0
∑fxy= 0
RVA – 20 + RB = 0
RVA + RB = 20 ----(1)
Taking moments at A
∑MA = 0
(20 × 3) – (RB × 5) = 0
60 – 5RB
RB = 12 kN
put in equation (1)
RVA + 12 = 20
RVA = 20-12
RVA = 8 kN
Question 2) Find support reaction for given beam
Answer 2)
Resolving forces horizontally
∑fx = 0
RHA = 0
Resolving forces vertically
∑fy= 0
RVA – 60 + RB = 0
RVA + RB = 60 -------(1)
Taking moment at A
∑MA = 0
(60 × 2) – (RB × 4 ) = 0
120 – 4RB = 0
RB = 
RB = 30 kN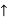
Que 3. Find the support reactions of a given loading for Beam.
Resolving forces horizontally
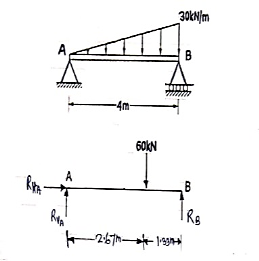∑fX = 0
RHA = 0
Resolving forces vertically
∑fY= 0
RVA – 60 + RB = 0
RVA + RB = 60 ----------------- (1)
Taking moments at A
∑ MA = 0
(RVA × 0) + (60 × 2.67) – 4RB = 0
160.2 – 4RB = 0
Put in equation (1)
We get
RVA + 40 = 60
RVA = 60 – 40
RVA = 20 kN
Que 4. Find the support reactions for given beam.
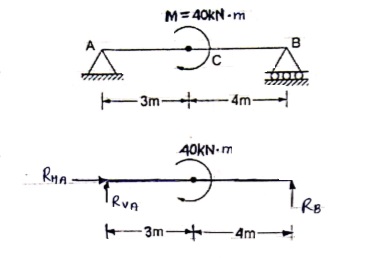
Resolving force horizontally
∑fX = 0
RHA = 0
Resolving forces vertically
∑fy = 0
RVA + RB = 0 ---------------(1)
Taking moments at A
40 – 7RB = 0
RB =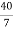 
RB = 5.71 kN
Put above value in equation (1)
RVA + RB = 0
RVA + 5.71 = 0
RVA = - 5.71 kN
RVA = 5.71 kN 
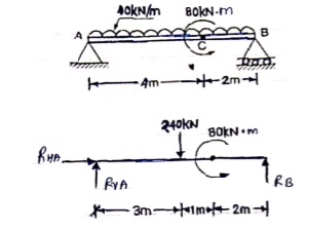
Resolving forces horizontally
∑fX = 0
RHA = 0
Resolving forces vertically
∑fy = 0
RVA – 240 + RB = 0
RVA + RB = 240 --------------(1)
Taking moment at A
∑ MA = 0
(240 × 3) – 80 – 6RB = 0
640 – 6RB = 0
RB = 106.67 kN
Put this value in equation (1)
RVA + RB = 240
RVA = 240 – 106.67
RVA = 133.33 kN
Que 5. Find support reactions for the loading as shown below:
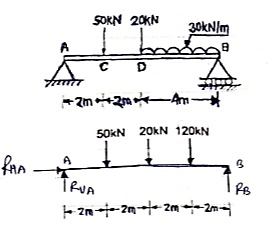
Resolving forces vertically
∑fy = 0
RVA – 50 – 20 – 120 + RB = 0
RVA + RB = 190 --------------(1)
Resolving forces horizontally
∑fX = 0
RHA = 0
Taking moments at A
∑ MA = 0
(50 × 2) + (20 × 4) + (120 × 6) – 8RB = 0
100 + 80 + 720 – 8RB = 0
900 – 8RB = 0
RB – 112.5 kN
Put above value in equation (1)
RVA + 112.50 = 190
RVA = 77.5 kN
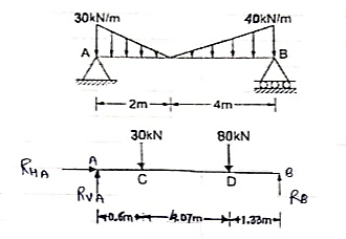
Que 6. Find the reactions at support A & B.
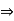Resolving forces vertically
∑fy = 0
RVA – 30 – 80 + RB = 0
RVA + RB = 110 ----------(1)
Resolving forces horizontally
∑fX = 0
RHA = 0
Taking moments at A
∑ MA = 0
(30 × 0.6) + [80 × (4.07 + 0.6)]- (6 × RB) = 0
18 + 373.6 – 6RB = 0
6RB = 391.6
RB= 65.267 kN
Put above value in equation (1)
RVA + RB = 110
RVA + 65.267 = 110
RVA = 110 – 65.267
RVA = 44.733 kN
