Unit - 4

Matrix Algebra- I

4.1 Definition of Matrix, types of matrices and their properties

1. Definition:

An arrangement of m.n numbers in m rows and n columns is called a matrix of order mxn.

Generally a matrix is denoted by capital letters. Like, A, B, C, ….. Etc.

2.     Types of matrices:- (Review)

1. Row matrix
2. Column matrix
3. Square matrix
4. Diagonal matrix
5. Trace of a matrix
6. Determinant of a square matrix
7. Singular matrix
8. Non – singular matrix
9. Zero/ null matrix
10. Unit/ Identity matrix
11. Scaler matrix
12. Transpose of a matrix
13. Triangular matrices

Upper triangular and lower triangular matrices,

14. Conjugate of a matrix

15. Symmetric matrix

16. Skew – symmetric matrix

3.     Operations on matrices:

1. Equality of two matrices
2. Multiplication of A by a scalar k.
3. Addition and subtraction of two matrices
4. Product of two matrices
5. Inverse of a matrix

4.     Elementary transformations

a)     Elementary row transformation

These are three elementary transformations

1. Interchanging any two rows (Rij)
2. Multiplying all elements in ist row by a non – zero constant k is denoted by KRi
3. Adding to the elements in ith row by the kth multiple of jth row is denoted by .

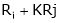b)    Elementary column transformations:

There are three elementary column transformations.

1. Interchanging ith and jth column. Is denoted by Cij.
2. Multiplying ith column by a non – zero constant k is denoted by kCj.
3. Adding to the element of ith column by the kth multiple of jth column is denoted by Ci + kCj.

Rank of a matrix:

Let A be a given rectangular matrix or square matrix. From this matrix select any r rows from these r rows select any r columns thus getting a square matrix of order r x r. The determinant of this matrix of order r x r is called minor or order r.

e.g.

If

For example select 2nd and 3rd row. i.e.

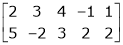
Now select any two columns. Suppose, 1st and 2nd.

i.e.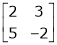

4.2           Determinant and their properties

Determinant :

In linear algebra, determinant is a special number that can be determined from a square matrix. The determinant of a matrix, say P is denoted de t(P), |P| or det P. Determinants have some properties that are useful as they permit us to generate the same results with different and simpler configurations of entries (elements). There are 10 main properties of determinants which include reflection property, all-zero property,  proportionality or repetition property, switching property, scalar multiple property, sum property, invariance property, factor property, triangle property, and co-factor matrix property. All the determinant properties have been covered below in a detailed way along with solved examples.

Properties of a determinant:

1. Reflection Property:

The determinant remains unaltered if its rows are changed into columns and the columns into rows. This is known as the property of reflection.

2. All-zero Property:

If all the elements of a row (or column) are zero, then the determinant is zero.

3. Proportionality (Repetition) Property:

If the all elements of a row (or column) are proportional (identical) to the elements of some other row (or column), then the determinant is zero.

4. Switching Property:

The interchange of any two rows (or columns) of the determinant changes its sign.

5. Scalar Multiple Property:

If all the elements of a row (or column) of a determinant are multiplied by a non-zero constant, then the determinant gets multiplied by the same constant.

6. Sum Property:

    =    + 

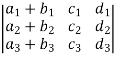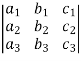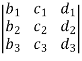
7. Property of Invariance:

   =   

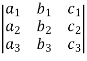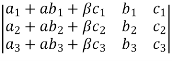
That is, a determinant remains unaltered under an operation of the form

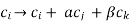, j ,k ≠ i or an operation of the form

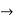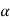R i Ri + Rj + 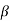R K , j, k ≠  i

8. Factor Property:

If a determinant Δ becomes zero when we put  X=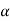 ,Then (x−α) is a factor of Δ.

9. Triangle Property:

If all the elements of a determinant above or below the main  diagonal consist of zeros, then the determinant is equal to the product of diagonal elements. That is,

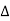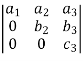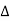=   =  1 =   =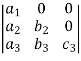  

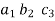
10. Determinant of cofactor matrix:

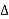      =    = , where 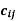denotes the co-factor of

The element 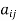    in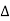

Example 1:

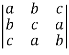  = ( a+b+c)(ab+bc+ca-a2 –b2 –c2)

Solution:

By using invariance and scalar multiple property we can prove the given problem.

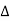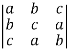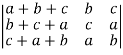=   =   c1 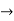c1+c2+c3

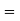(a+b+c)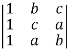

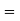(a+b+c)  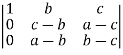 R2 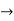R2 – R1  and R3 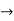R3 – R1

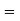(a+b+c)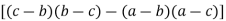

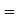(a+b+c)(ab+bc+ca-a2-b2 –c2)

Example 2:

Prove the following identity.,

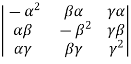= 4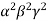

Solution:

Take 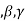, from the L.H.S and then by using scalar multiple property and in-variance property of determinant. We can prove the given problem

=

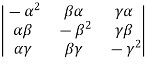
Taking 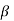 ,,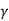 common from c1,c2,c3 respectively

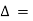
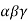
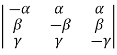
Now taking 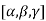common from R1,R2 ,R3 respectively.

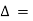
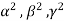
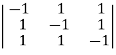
Now applying R3  R3+R1  we have =

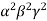
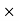
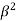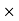
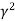Now expanding along c1 ,

(-1)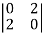 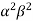(-1) =  (-1)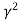 (0-4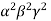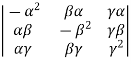)=4

      =4.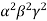

Hence  proved.

4.3           Rank and nullity of a matrix

The rank of a matrix is the largest order of the non zero minor of the matrix( we search at least one non zero minor  to find the rank of the matrix).

A matrix A is said to have the rank r if and only if there exist at least one non zero minor of the given matrix of order r and every minor greater than order r is zero.

This is denoted by .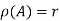

Normal form of a matrix:

Every non singular matrix A of rank r can be converted by applying sequence of the elementary transformation in the form of

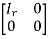
Is called the normal form of the matrix A.

Also the rank of a matrix can be calculated by converting it into normal form then the order of identity matrix obtained is the rank of the given matrix.

Example1: Reduce the following matrix into normal form and find its rank,

Let A =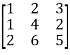

Apply 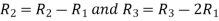we get

A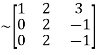 

Apply 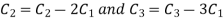we get

A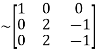 

Apply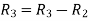

A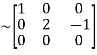 

Apply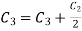

A 

Apply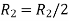 

A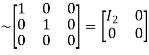 

Hence the rank of matrix A is 2 i.e. .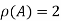

Example2: Reduce the following matrix into normal form and find its rank,

Let A =   

Apply 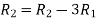and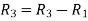

A

Apply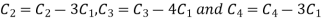

A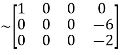

Apply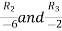

A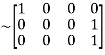

Apply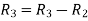

A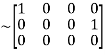

Apply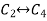

A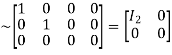

Hence the rank of the matrix A is 2 i.e. .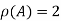

Example3: Reduce the following matrix into normal form and find its rank,

Let A =

Apply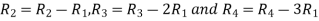

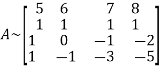
Apply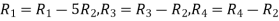

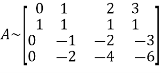
Apply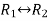

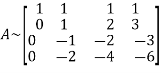
Apply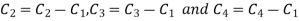 

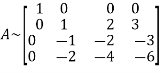
Apply 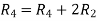and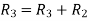

Apply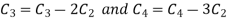

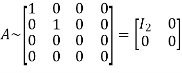
Hence the rank of matrix A is 2 i.e. .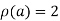

4.4           Determination of rank

Two square matrix 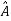and A of same order n are said to be similar if and only if

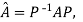for some non-singular matrix P.

Such transformation of the matrix A into 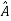with the help of non singular matrix P is known as similarity transformation.

Similar matrices have the same Eigen values.

If X is an Eigen vector of matrix A then 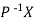is Eigen vector of the matrix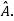  

Reduction to Diagonal Form:

Let A be  a square matrix of order n has n linearly independent Eigen vectors  which form the  matrix P such that

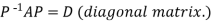
Where P is called the modal matrix and D is known as spectral matrix.

Procedure: let A be a square   matrix of order 3.

Let three Eigen vectors of A are 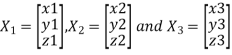 corresponding  to  Eigen values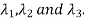

Let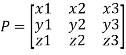     

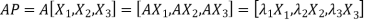  {by characteristics equation of A}

Or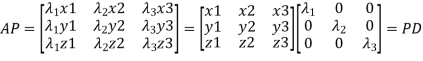

Or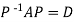 

Note: The method of diagonalization is helpful in calculating power of a matrix.

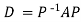  .Then for an integer n we have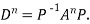  

We are using the example of 1.6*

Example1:  Diagonalize the matrix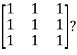

Let A=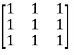

The three Eigen vectors obtained are  (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values .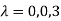

Then 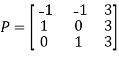   and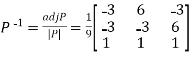

Also we know that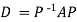    

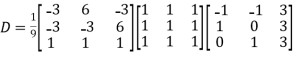
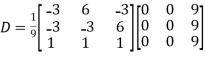
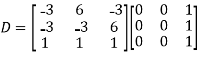
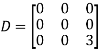
Example2: Diagonalize the matrix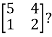

Let A =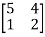

The Eigen vectors are (4,1),(1,-1) corresponding to Eigen values .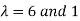

Then 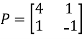   and also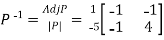 

Also we know that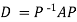    

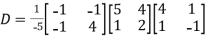
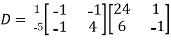
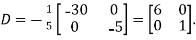
4.5           Gauss Jordan method for computing inverse, Triangularization of Matrices by Gauss Elimination Process

Given a Matrix, the task is to find the inverse of this Matrix using the Gauss-Jordan method.

What is matrix?

Matrix is an ordered rectangular array of numbers.

3 3 rectangular matrix

Operations that can be performed on a matrix are: Addition,

The matrix must be a non-singular matrix and,

1. There exist an Identity matrix I for which 

In general, the inverse of n X n matrix A can be found using this simple formula:
 

A-1 =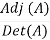

Where, Adj(A) denotes the adjoint of a matrix and, Det(A) is Determinant of matrix A.

Methods for finding Inverse of Matrix:

Finding the inverse of a 2×2 matrix is a simple task, but for finding the inverse of larger matrix (like 3×3, 4×4, etc) is a tough task, So the following methods can be used:

1. Elementary Row Operation (Gauss-Jordan Method) (Efficient)
2. Minors, Cofactors and Ad-jugate Method (Inefficient)

Elementary Row Operation (Gauss – Jordan Method):

Gauss-Jordan Method is a variant of Gaussian elimination in which row reduction operation is performed to find the inverse of a matrix.

Steps to find the inverse of a matrix using Gauss-Jordan method:

In order to find the inverse of the matrix following steps need to be followed:

1. Form the augmented matrix by the identity matrix.
2. Perform the row reduction operation on this augmented matrix to generate a row reduced echelon form of the matrix.
3. The following row operations are performed on augmented matrix when required:
   • Interchange any two row.
   • Multiply each element of row by a non-zero integer.
   • Replace a row by the sum of itself and a constant multiple of another row of the matrix.

Example 1:

GIVEN 33 RECTANGULAR MATRIX 

The augumented matrix is as follows

• After applying the Gauss-Jordan elimination method:

The inverse of a matrix is as follows .,

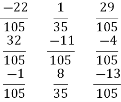
EXAMPLE 2:

Find the inverse of

A=    

Solution:

Step 1: Adjoin the identity matrix to the right side of A:

Step 2: Apply row operations to this matrix until the left side is reduced to I. The computations are:

              R2  R2-R1  , R3 R3-R1

             R3 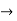 R3 + 2R2

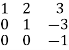
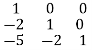        R1R1 -3R3  , R2 R2+3R3

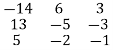     R1R1-2R2

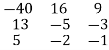
Step 3: Conclusion: The inverse matrix is:

A-1 =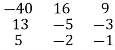

4.6 Solution of system of linear equations

Invariance of rank through elementary transformations.

1. The rank of matrix remains unchanged by elementary transformations. i.e. from a matrix. A we get another matrix B by using some elementary transformation. Then

Rank of A = Rank of B

2.     Equivalent matrices:

The matrix B is obtained from a matrix A by a sequence of a finite no. Of elementary transformations is said to be equivalent to A. And we write.

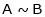
Normal form or canonical form:

Every mxn matrix of rank r can be reduced to the form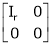

By a finite sequence of elementary transformation. This form is called normal form or the first canonical form of the matrix A.

Ex. 1

Reduce the following matrix to normal form of Hence find it’s rank,

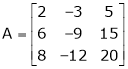
Solution:

We have,

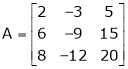
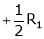
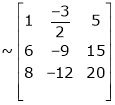
Apply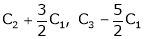

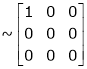
Rank of A = 1

Ex. 2

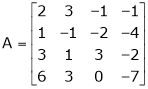
Find the rank of the matrix

Solution:

We have,

Apply R12

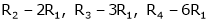
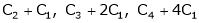
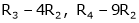
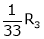
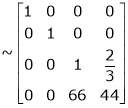
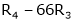
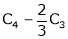
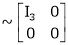
Rank of A = 3

Ex. 3

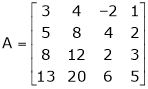
Find the rank of the following matrices by reducing it to the normal form.

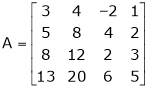
Solution:

Apply C14

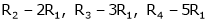
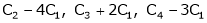
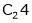
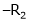
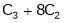
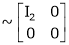
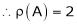
H.W.

Reduce the follo9wing matrices in to the normal form and hence find their ranks.

a)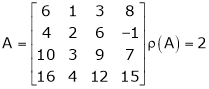    

b)   

5.     Reduction of a matrix a to normal form PAQ.

If A is a matrix of rank r, then there exist a non – singular matrices P & Q such that PAQ is in normal form.

i.e.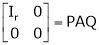

To obtained the matrices P and Q we use the following procedure.

Working rule:-

1. If A is a mxn matrix, write A = Im A In.
2. Apply row transformations on A on l.h.s. And the same row transformations on the prefactor Im.
3. Apply column transformations on A on l.h.s and the column transformations on the postfactor In.

So that A on the l.h.s. Reduces to normal form.

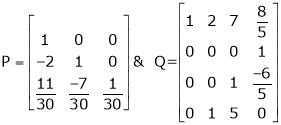
Example 1

If 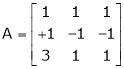Find Two

Matrices P and Q such that PAQ is in normal form.

Solution:

Here A is a square matrix of order 3 x 3. Hence we write,

A = I3 A.I3

i.e.

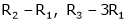
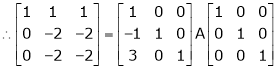
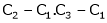
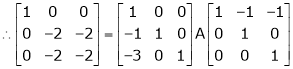
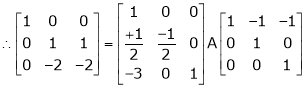
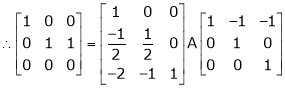
i.e.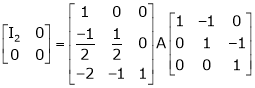

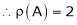
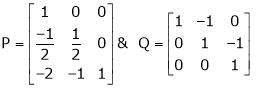
Example 2

Find a non – singular matrices p and Q such that P A Q is in normal form where

Solution:

Here A is a matrix of order 3 x 4. Hence we write A as,

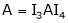
i.e.

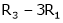
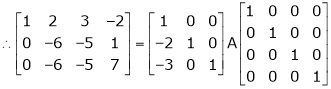
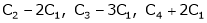
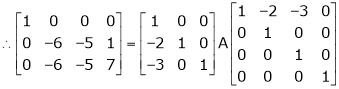
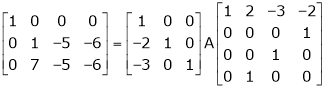
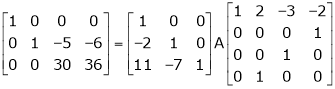
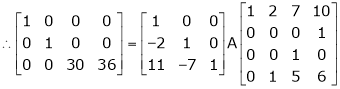
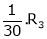
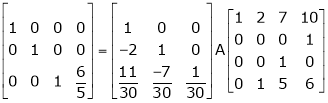
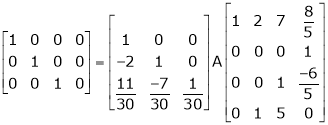
i.e.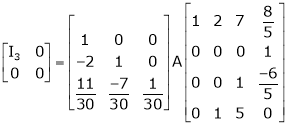

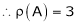
Reference Books

1. M.D. Wier, et. Al., Thomas’ Calculus, 11th Ed., Pearson Education, 2008

2. Stewart James, Calculus Early Transcendental, 5th Ed., Thomson India, 2007

3. Wylie & Barrett, Advanced Engineering Mathematics, Mc graw Hill pub.

4. Greenberg, M.D., Advanced Engineering Mathematics, 2nd ed., Pearson