UNIT 1
Introduction
Mechanics is a branch of the physical sciences concerned with the state of rest or motion of bodies that are subjected to the action of forces. The study of mechanics involves many more subject areas. However, initial study is usually split into two areas; statics and dynamics.
Statics is concerned with bodies that are either at rest or move with a constant speed in a fixed direction. Dynamics deals with the accelerated motion of bodies. Statics can therefore be considered as a special case of dynamics where the acceleration is zero. In engineering, since many objects are designed with the intention that they are at rest or their motion remains constant, statics deserves special treatment.
Scalars and vectors
In mechanics, as elsewhere, some quantities are scalar quantities and some are vector quantities. It is important to understand the difference between the two.
Scalars
Scalar quantities are quantities that only have a magnitude (size). Scalar quantities are useful, but for some quantities in mechanics we need more information; to this end we introduce vectors.
Vectors
Vector quantities are quantities that possess direction, as well as magnitude. Vectors are usually referred to in bold type
Basic concepts
Basic quantities
Time is the measure of a succession of events and is a basic quantity in dynamics. Time is not involved in the analysis of statics problems. Time is a scalar quantity.
Length is needed to locate the position of a point in space and describes the size of a physical system. Once a standard unit of length has been defined, it is possible to define distances and geometric properties of a body as a multiple of the unit of length. Length is a scalar quantity.
Volume is a measurement of the physical size of an object. It refers to how much space an object takes up. Volume is a scalar quantity.
Mass is a different measurement of the size of an object. The mass, measured in kilograms, depends only on the amount of matter forming the body. Mass is a scalar quantity.
Density is related to mass and volume. It is defined as the mass per unit volume. This means that an object that has a large mass but a small volume will have a large density. Density is a scalar quantity.
Speed is a measure of how quickly a body is moving. It is defined as distance travelled per unit time. Speed is a scalar quantity.
Forces are influences on a body or system which, acting alone, would cause the motion of that body or system to change. A system or body at rest and then subjected to a force will start to move. To work with forces we need to know the magnitude (size), direction and the point of application of the force. Forces are vector quantities.
Displacement is a measure of distance in a particular direction. Displacement is a vector quantity.
Velocity is the rate of change of displacement with respect to time. Velocity is a vector quantity.
Acceleration is the rate of change of velocity with respect to time. Acceleration is a vector quantity.
Momentum is defined as the product of an object’s mass and its velocity. This is a very important quantity in mechanics. It arises in many problems particularly those involving collisions. Momentum is a vector quantity.
Idealisations
In mechanics we look at real life situations and try to predict what will happen. The problem with real life is that it is often quite complicated. When studying problems in mechanics we often make idealisations of real life situations that simplify the problem. There are many commonly used idealisations that we will introduce in later sheets. Here follows a list of some common idealisations that are used in mechanics.
Particles are bodies which can be treated as a point mass in a given context. For example, when modelling the motion of the planets around the Sun, the planets and Sun can be treated as particles. Much of basic mechanics study is concerned with objects that can be treated as particles.
Connected particles arise in problems where two objects are attached in some way and both objects can be treated as particles. For example, two masses, connected by a string which passes over a pulley could be modelled as connected particles.
Rigid bodies can be considered as combinations of particles in which all the particles remain at a fixed distance from one another both before and after applying a force i.e. there is no bending or stretching. For example a brick can in most circumstances be thought of as a rigid body. Many real life objects can be considered to be rigid bodies to a good approximation.
Fundamental concept
Certain concepts and definitions are basic to the study of mechanics and they should be understood at the outset. The basic concepts in mechanics are space, time, mass and force. These concepts cannot be truly defined. They should be accepted on the basis of our intuition and experience, and used as a mental frame of reference for our study of mechanics.
In Newtonian mechanics, space, time and mass are absolute quantities, which mean that they are independent of each other (this is not true in RelativisticMechanics, where the time of an event depends upon its position and the mass of
a body varies with its velocity) and cannot be defined in terms of other quantities
Or in simpler terms. Force is a derived quantity.
Space: is the geometric region occupied by bodies whose positions are described by linear or angular measurements relative to a specific coordinate system. For three dimensional problems, three independent coordinates are needed. For two dimensional problems only two coordinates will be required.
Time: is a concept for measuring the succession and the duration of events. Time
Is not directly involved in the analysis of problems in Statics.
Mass: is a measure of the translational inertia of the body, which is its resistance
To a change in velocity. Mass can also be thought of as the quantity of matter in a
Body. The mass of a body affects the gravitational attraction force between it and other bodies. The concept of mass is used to characterize and compare two bodies on the basis of certain fundamental mechanical experiments depending on the definitions given above.
For example:
1) Two bodies of the same mass will be attracted by the Earth in the same manner.
2) They will also offer the same resistance to a change in translational motion.
Force: A force represents the action of one body on another. Force can be generated either by the direct contact of bodies or by their effect at a distance.
Forces always occur in pairs. Forces of a pair are always equal in magnitude and opposite in direction. Force is a vector quantity. The action of a force is characterized by its magnitude, by the direction of its action and by its point of application. A force tends to move a body in the direction of its action (the push – pull effect of the force). In addition, a force tends to rotate the body about any axis which does not intersect the line of action of the force and which is not parallel to it (the moment effect of the force).
Idealization in Mechanics:
The mathematical description of a real engineering Problem can become very complex. Thus, idealization (or models) and assumptions are used in mathematics in order to simplify the application of the theory.
1) Particle: is a body of negligible dimensions. In the mathematical sense, a particle is a body whose dimensions are considered to be near zero so that we may analyse it as a mass concentrated at a point. We often choose a particle as a differential element of the body. We may treat a body as a particle when its dimensions are irrelevant to the description of its position or the action of forces applied to it. A body considered as a particle is taken as a unique point, which is generally the mass center of the body. A particle has mass but no shape and dimensions. In so doing, the principles of mechanics are reduced to a rather simplified form, since the geometry of the body will not be involved in the analysis of the problem. The line of actions of all the forces applied to the body must pass through this point.
Forces can only exert push – pull effects on a particle.
2) Rigid Body: is an idealized body composed of a large number of particles all of which always remain at fixed distances from each other. In addition to the tendency to move a body in the direction of its application, a force may also tend to rotate a body about an axis. A rigid body is assumed to undergo no deformation under the action of applied forces. Its shape and dimensions remain fixed under all loading conditions and at all times.
3) Point Force: is an idealized force assumed to act at a point on a body. A constant force exerted on a body by another is actually distributed over the area of contact between two bodies. If the area of contact is relatively small, the contact force between the two bodies may be considered as a point (concentrated) force.
The Fundamental Concepts
The four fundamental concepts used in mechanics are space, time, mass and force1. It is not easy to define what these concepts are. Rather, one “knows” what they are, and they take on precise meaning when they appear in the principles and equations of mechanics discussed further below.
The concept of space is associated with the idea of the position of a point, which is
Described using coordinates (x, y, z) relative to an origin o as illustrated in Fig.
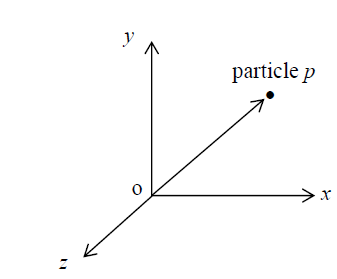
Figure 2.3a: a particle in space
The time at which events occur must be recorded if a material is in motion. The concept of mass enters Newton’s laws (see below) and in that way is used to characterize the relationship between the acceleration of a body and the forces acting on that body. Finally, a force is something that causes matter to accelerate; it represents the action of one body on another.
The Fundamental Principles
The fundamental laws of mechanics are Newton’s three laws of motion. These are:
Newton’s First Law:
If the resultant force acting on a particle is zero, the particle remains at rest (if originally at rest) or will move with constant speed in a straight line (if originally in motion) By resultant force, one means the sum of the individual forces whichact; the resultant is obtained by drawing the individual forces end-to-end, in what is known as the vectorpolygon law; this is illustrated in Fig. 2.3b , in which three forces 1 2 3 F , F , F act on a single particle, leading to a non-zero resultant force F.
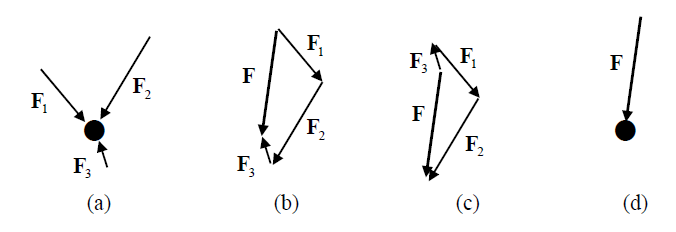
Figure 2.3b: the resultant of a system of forces acting on a particle; (a)
Three forces acting on a particle, (b) construction of the resultant F, (c)
An alternative construction, showing that the order in which the forces
Are drawn is immaterial, (d) the resultant force acting on the particle
Example (illustrating Newton’s First Law)
In Fig. 2.3c is shown a floating boat. It can be assumed that there are two forces acting on the boat. The first is the boat’s weight g F. There is also an upward buoyancy force b F exerted by the water on the boat. If these two forces are equal and opposite, the resultant of these two forces will be zero, and therefore the boat will remain at rest (it will not move up or down).
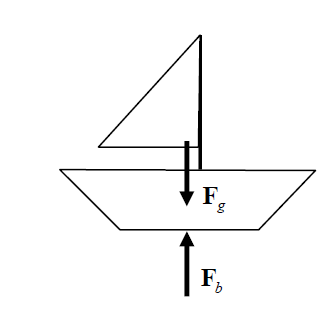
Figure 2.3c: a zero resultant force acting on a boat
The resultant force acting on the particle of Fig. 2.3b is non-zero, and in that case one applies Newton’s second law:
Newton’s Second Law:
If the resultant force acting on a particle is not zero, the particle will have an acceleration proportional to the magnitude of the resultant force and in the direction of this resultant force:
F = ma
Where F is the resultant force, a is the acceleration and m is the mass of the particle. The units of the force are the Newton (N), the units of acceleration are metres per second squared (m/s2), and those of mass are the kilogram (kg); a force of 1 N gives a mass of 1 kg an acceleration of 1 m/s2.
If the water were removed from beneath the boat of Fig. 2.3c, a non-zero resultant force would act, and the boat would accelerate downward4.
Newton’s Third Law:
Each force (of “action”) has an equal and opposite force (of “reaction”)
Again, considering the boat of Fig. 2.1.3, the water exerts an upward buoyancy force on the boat, and the boat exerts an equal and opposite force on the water. This is illustrated
In Fig. 2.3d
.
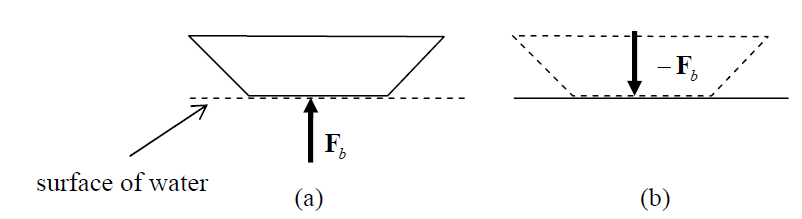Figure 2.1.4: Newton’s third law; (a) the water exerts a force on the
Boat, (b) the boat exerts an equal and opposite force on the water
Newton’s laws are used in the analysis of the most basic problems and in the analysis of the most advanced, complex, problems. They appear in many guises and sometimes they appear hidden, but they are always there in a Mechanics problem.
1) The Parallelogram Law: Two vectors A and Btreated as free vectors, can be replaced by their equivalent R which is the diagonal of the parallelogram formed by A and B as its two sides, as shown. Ris called the resultant of A and B
Hence, the combined effect of two forces A and B (for example acting on a particle) is equivalent to the effect of their resultant.
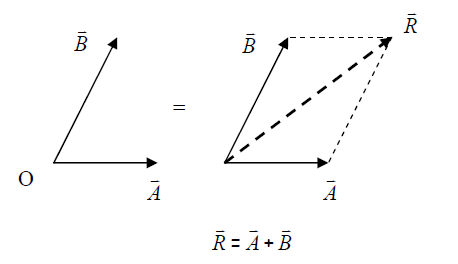
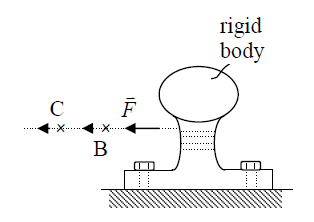
2) The Principle of Transmissibility: The effect of a force on a rigid body will remain unchanged if the forced is moved to act on its line of action. In other words, a force may be applied at any point on its given line of action without altering the resultant effects on the rigid body on which it acts.
3) Newton’s First Law: If the resultant force acting on a particle is zero, then the particle is in equilibrium. Stated mathematically as (∑F = 0), where ∑Fis thevector sum (the resultant) of all the forces acting on the particle.
4) Newton’s Second Law: The acceleration of a particle is proportional to the resultant force acting on it and is in the direction of this force.
∑F = ma
5) Newton’s Third Law: The forces of action and reaction between interacting bodies are equal in magnitude, opposite in direction and collinear.
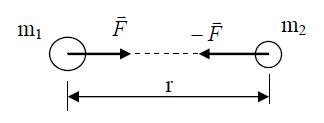
6) Newton’s Law of Gravitation: This law states that two particles of mass m1 and m2 are mutually attracted with equal and opposite forces F and - Fof magnitude F, given by theFormula.
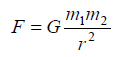
Where,
“r” is the centroidal distance between the two particles “G” is the universal constant of gravitation equal to 6.67 x 10-11 m3/kgs2
A particular case of great importance is that of the attraction of the Earth on a particle located at its surface. The force F exerted by the Earth on the particle is then defined as the weight W of the particle.
W = mg
Where,
“m” is the mass of the particle
“g” is the gravitational acceleration of the Earth
Scalar Quantities: The physical quantities which are specified with the magnitude or size alone are scalar quantities. For example, length, speed, work, mass, density, etc.
Vector Quantities: Vector quantities refer to the physical quantities characterized by the presence of both magnitude as well as direction. For example, displacement, force, torque, momentum, acceleration, velocity, etc.
Characteristics of Vectors
The characteristics of vectors are as followed –
- They possess both magnitudes as well as direction.
- They do not obey the ordinary laws of Algebra.
- These changes if either the magnitude or direction change or both change.
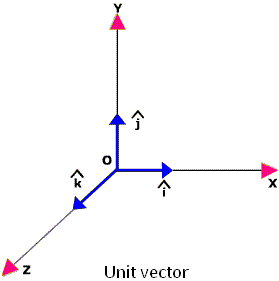
Unit Vector
A unit vector is that vector which is a vector of unit magnitude and points in a particular direction. The unit vector in the direction of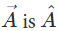
and is defined by
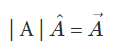
The unit vectors along the x, y and z-axis is ^i, ^j, and ^k respectively.
Equal Vectors
Vectors A and B are equal if | A | = | B | as well as their directions, are same.
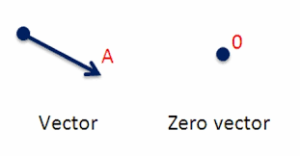
Zero Vectors
Zero vectorsare a vector with zero magnitudes and an arbitrary direction is a zero vector. It can be represented by O and is a Null Vector.
Negative of a Vector
The vector whose magnitude is same as that of a (vector) but the direction is opposite to that of a (vector) is referred to as the negative of a ( vector ) and is written as – a ( vector ).
Parallel Vectors
A and B are said to be parallel vectors if they have the same direction, or may or may not have equal magnitude ( A || B ). If the directions are opposite, then A ( vector) is anti-parallel to B ( vector ).
Coplanar Vectors
If the vectors lie in the same plane or they are parallel to the same plane, the vectors are said to be coplanar. If not, the vectors are said to be non – planar vectors.
Displacement Vectors
The displacement vector refers to that vector which gives the position of a point with reference to a point other than the origin of the coordinate system.
Vector Addition and Subtraction
After understanding what is a vector, let’s learn vector addition and subtraction. The addition and subtraction of vector quantities does not follow the simple arithmetic rules. A special set of rules are followed for the addition and subtraction of vectors. Following are some points to be noted while adding vectors:
- Addition of vectors means finding the resultant of a number of vectors acting on a body.
- The component vectors whose resultant is to be calculated are independent of each other. Each vector acts as if the other vectors were absent.
- Vectors can be added geometrically but not algebraically.
- Vector addition is commutative in nature, i.e
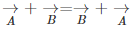
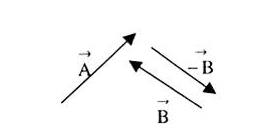
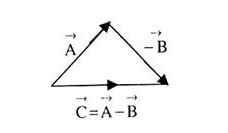
Now, talking about vector subtraction, it is the same as adding the negative of the vector to be subtracted. TO better understand, let us look at the example given below.Let us consider two vectors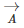 
and 
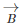as shown in the figure below. We required to subtract 
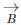from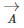 
It is just the same as adding 
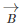and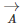 
The resultant is shown in the figure below
Vector Notation
For vector quantity usually, an arrow is used on the top like →v which represents the vector value of the velocity and also explains that the quantity has both magnitudes as well as direction.
Unit Vector:
Unit vector is a vector along any direction (according to our choice) and, it has a magnitude of one (1) unit.
It is used just to specify the direction.
For any vector, A, the unit vector can be written as :
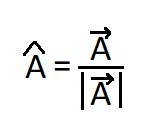
i.e.
Unit vector = vector / magnitude of the vector.
Position Vector:
As the name suggests, it is a vector, which signifies the position of a body (or a point) with respect to the origin (or with respect to a certain point).
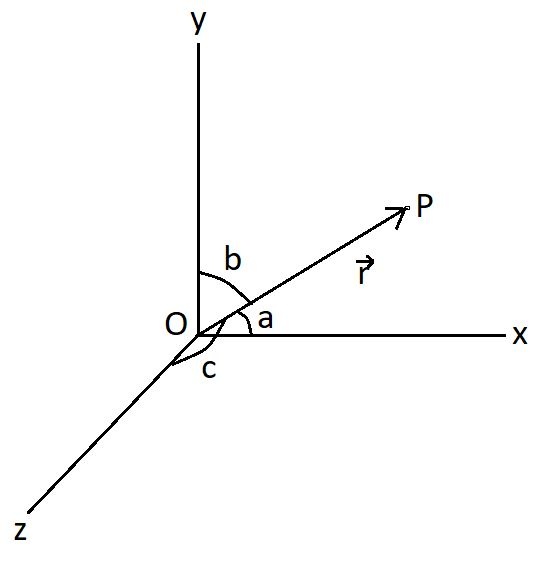
Vector r is the position vector of the point P with respect to the origin O and a, b, c are the angles with the x, y and z axis
So, r = r cos a i + r cos b j + r cos c kis the position vector of point P
A convenient way to specify the position of an object is with the help of a coordinate system. We choose a fixed point, called the origin and three directed lines, which pass through the origin and are perpendicular to each other. These lines are called the coordinate axes of a three-dimensional rectangular (Cartesian) coordinate system and are labelled the x-, y-, and z-axis. Three numbers with units specify the position of a point P. These numbers are the x-, y-, and z-coordinates of the point P. The coordinates of the point P in the diagram to the right are (a, b, c).
The coordinates of the point P are the components of the position vector. A unit vector pointing in the x-direction has a x-component of 1 and y- and z- components of zero. It is denoted by i. Similarly, a unit vector pointing in the y-direction is denoted by j, and a unit vector pointing in the z-direction is denoted by k. Unit vectors are direction indicators.
The components of any vector add up to form the vector itself.
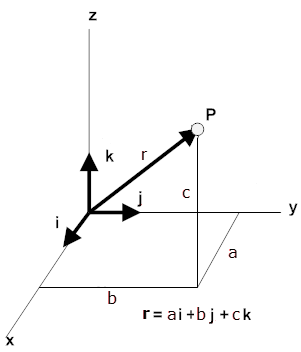
The position vector of a point P with coordinates (a, b, c) may be written in terms of its components as
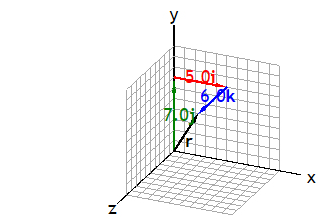
r = ai + bj + ck.
The magnitude of the position vector is its length r. It depends on the choice of the origin of the coordinate system. It is the straight-line distance of P from the origin.Below is a 3D representation of a position vector r = ai + bj +ck
A vector can be resolved into many different vectors, for resolution of vectors. For Example: Let us consider two numbers, say, 4 and 6, which is further added to obtain 10. Further, now 10 is broken or resolved. However, the number 10 can also be resolved into many other numbers like 10 = 5 + 5; 10 = 3 + 7 etc.
In a similar way, a vector can essentially be further broken or resolved to obtain multiple vectors of different magnitudes and directions. In Physics, vectors would be mainly resolved only along the coordinate axes, X, Y, and Z.
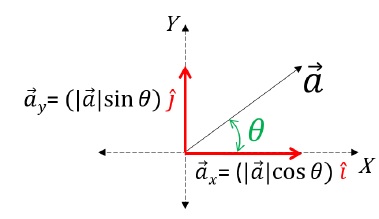
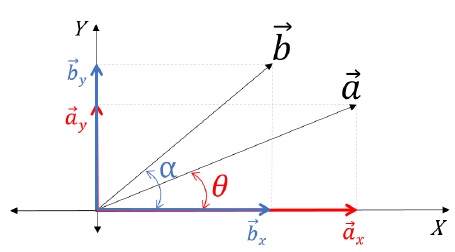
Resolving Vectors along X and Y Axis
To resolve a vector on an X-Y plane, first, draw the vector. Then, label and create the constructions on the figure as mentioned below:
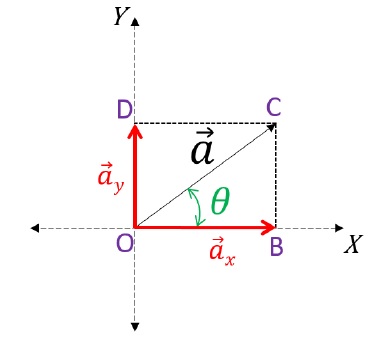
The complete figure seems to be like a parallelogram, further applying the Parallelogram law of vector addition. Herein, the two vectors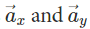 
appears to be added by the parallelogram law of vector addition to obtain 
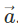Therefore, with this, we can say that
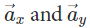are the resolved output of 
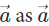has been again broken back to its components. Here,
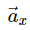is the x-component; and
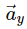is the y-component of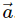 
In order to find the magnitudes of each component, in △OBC:
cos θ = OBOC
Therefore, OB = OC cos θ
Hence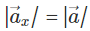
cos θ [ Magnitude of x – component ]
Sinθ = BCOC
So, BC = OC sin θ;
Also, BC = OD ( Opposite sides of Rectangle );
Therefore,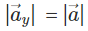
sin θ [ Magnitude of y – component ]
Note
The General Rule of Thumb states that the subtended angle will always touch one of the components. Further, the component which the given angle touches or the given angle is subtended with will be the cos component of the given vector. Whereas the other will automatically be the sin component.
Unit Vectors along Co-ordinate Axes
For the co-ordinate axes, there are special unit vectors designated by convention î, ĵ, and k̂, which respectively represents X, Y, and Z axes. By the property of unit vectors, |î| = |ĵ| = |k̂| = 1
Writing Vectors in Component Form: Using Coordinate Axes Unit Vectors
A vector can be expressed as a product of its magnitude and direction. Therefore,
Addition of Vectors and Subtraction of Vectors in Component Form (Expressed as Unit Vectors)
Consider the following figure:
A system of units is a set of related units that are used for calculations. The system includes base units, which represent base dimensions, and derived units, which represent products of powers of base dimensions. Some units exist in more than one system of units. For example, there is a unit of mass named the ounce in the avoirdupois and troy systems of units. To distinguish between these units in Maple, each unit has a context. For example, the ounce[avoirdupois] and ounce[troy] are units of mass. For additional information about dimensions, units, and contexts, see Details.
For example, in the MKS system, the base units are the meter, kilogram, and second, which represent the base dimensions of length, mass, and time, respectively. In this system, the unit of speed is the meter per second. However, the unit of force, the kilogram meter per square second, is named the newton.
In the FPS system, the base units are the foot, pound, and second, which represent the base dimensions of length, mass, and time, respectively. The complex unit of speed and derived unit of force are the foot per second and pound, respectively, where 1 poundequals 1 foot pound per second squared.
Systems of Units
The set of systems of units in Maple is:
SI (International System of Units) (meter-kilogram-second-ampere-kelvin-mole-candela)
FPS (foot-pound-second)
MKS (meter-kilogram-second)
CGS (centimeter-gram-second)
EMU (Electromagnetic) (centimeter-gram-second-ampere)
ESU (Electrostatic) (centimeter-gram-second-abcoulomb)
Atomic (bohr-electron mass-atomic second-electron)
MTS (meter-tonne-second)
