Unit III
Measures of dispersion and skewness
Absolute measures of Dispersion Range:
It gives an idea about the amount of dispersion in a set of observations. It measures the dispersion in the same units as the units of original data. Absolute measures cannot be used for comparison of two or more data set variations.
- Range – Range defines the difference between the maximum value and the minimum value given in a data set. More the range , group is more variable. The smaller the range the more homogenous is the group.
R = H – L
Example 1 – 5, 10, 15, 20, 7, 9, 17, 13, 12, 16, 8, 6
Range = H-L
=20 – 5 = 15
Coefficient of range –

Coefficient of range = (15/(20+5))*100 = 60
Example 2 – what is the range for the following set of numbers?
15,21,57,43,11,39,56,83,77,11,64,91,18,37
Solution
Range = H-L
= 91 – 11 = 80
Therefore the range is 80
Example 3 – the frequency table shows the number of goals the lakers scored in their last twenty matches. What was the range
No. Of goals | Frequency |
0 | 2 |
1 | 3 |
2 | 3 |
3 | 6 |
4 | 3 |
5 | 1 |
6 | 1 |
7 | 1 |
Solution
The range is the difference between the lowest and highest values.
The highest value was 7 (They scored 7 goals on 1 occasion)
The lowest value was 0 (They scored 0 goals on 2 occasions)
Therefore the range = 7 - 0 = 7
Example 4 – the following table shows the sales of DVD players made by a retail store each month last year
Month | No. Of sales |
January | 25 |
Feb | 43 |
March | 39 |
April | 28 |
May | 29 |
June | 35 |
July | 32 |
August | 46 |
September | 28 |
October | 43 |
November | 51 |
December | 63 |
Solution
The range is the difference between the lowest and highest values.
The lowest number of sales = 25 in January
The highest number of sales = 63 in December
So the range = 63 - 25 = 38
Example 5 – what is the range for the following set of numbers?
57, -5, 11, 39, 56, 82, -2, 11, 64, 18, 37, 15, 68
Solution
The range is the difference between the lowest and highest values.
The highest value is 82.
The lowest value is -5.
Therefore the range = 82 - (-5) = 82+5 = 87
Merits
- Simple and easy to understand
- It gives a quick answer
Demerits
- It is not based on all observation
- Affected by sampling fluctuations
- It cannot be calculated in open ended distributions
2. Interquartile range - The interquartile range measures the range of the middle 50% of the values only. It is calculated as the difference between the upper and lower quartile.
Interquartile range = upper quartile – lower quartile
= Q3 – Q1
Examples 1– find the interquartile range for 1, 2, 18, 6, 7, 9, 27, 15, 5, 19, 12.
Solution
Arrange the numbers in ascending order
1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27
Find the median
Median = 9
(1, 2, 5, 6, 7), 9, (12, 15, 18, 19, 27)
Q1 as median in the lower half and Q3 as median in the upper half
Q1 = median in (1, 2, 5, 6, 7)
Q1 = 5
Q3 = median in (12, 15, 18, 19, 27)
Q3 = 18
Interquartile range = 18 – 5 = 13
Example 2 –Find the interquartile for the following data set: 3, 5, 7, 8, 9, 11, 15, 16, 20, 21.
Solution
Arrange the numbers in ascending order
3, 5, 7, 8, 9, 11, 15, 16, 20, 21
Make a mark in the centre of the data:
(3, 5, 7, 8, 9,) | (11, 15, 16, 20, 21)
Find the median
Q1 = 7
Q3 = 16
Interquartile range = 16 – 7 = 9
Example 3 - find the interquartile for the following data set: 1, 3, 4, 5, 5, 6, 7, 11
Make a mark in the centre of the data:
(1, 3, 4, 5,)(5, 6, 7, 11)
Find the median
Q1 = (3+4)/2 = 3.5
Q3 = (6+7)/2 = 6.5
Interquartile range = 6.5 – 3.5 = 3
Example 4 -
Find the interquartile range for odd sample size
63,64,64,70,72,76,77,81,81
Solution
Make a mark in the centre of the data:
(63,64,64,70,)72,(76,77,81,81)
Find the median
Q1 = (64+64)/2 = 64
Q3 = (77+81)/2 = 79
Interquartile range = 79 – 64 = 15
Relative measures of Dispersion Range:
The relative measures of distribution are used for comparing the distribution of two or more data sets.
Coefficients of dispersion are used to compare two series with different measurement of unit
Quartile Deviation:
Quartile deviation is the product of half of the difference between the upper and the lower quartiles.
QD = (Q3 - Q1) / 2
Coefficient of Quartile Deviation = (Q3 –Q1) / (Q3 + Q1)
Quartile deviation for ungrouped data
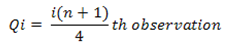
Examples 1
Day | Frequency |
1 | 20 |
2 | 35 |
3 | 25 |
4 | 12 |
5 | 10 |
6 | 23 |
7 | 18 |
8 | 14 |
9 | 30 |
10 | 40 |
Solution
Arrange the frequency data in ascending order
Day | Frequency |
1 | 10 |
2 | 12 |
3 | 14 |
4 | 18 |
5 | 20 |
6 | 23 |
7 | 25 |
8 | 30 |
9 | 35 |
10 | 40 |
First quartile (Q1)
Qi= [i * (n + 1) /4] th observation
Q1= [1 * (10 + 1) /4] th observation
Q1 = 2.75th observation
Thus, 2.75th observation lies between the 2nd and 3rd value in the ordered group, between frequency 12 and 14
First quartile (Q1) is calculated as
Q1 = 2nd observation +0.75 * (3rd observation - 2nd observation)
Q1 = 12 + 0.75 * (14 – 12) = 13.50
Third quartile (Q3)
Qi= [i * (n + 1) /4] th observation
Q3= [3 * (10 + 1) /4] th observation
Q3 = 8.25th observation
So, 8.25th observation lies between the 8th and 9th value in the ordered group, between frequency 30 and 35
Third quartile (Q3) is calculated as
Q3 = 8th observation +0.25 * (9th observation – 8th observation)
Q3 = 30 + 0.25 * (35 – 30) = 31.25
Now using the quartiles values Q1 and Q3, we will calculate the quartile deviation.
QD = (Q3 - Q1) / 2
QD = (31.25 – 13.50) / 2 = 8.875
Coefficient of Quartile Deviation = (Q3 –Q1) / (Q3 + Q1)
= (31.25 – 13.50) /(31.25 + 13.50) = 0.397
Example 2 – calculate quartile deviation from the following test scores
Sl. N o | Test scores |
1 | 17 |
2 | 17 |
3 | 26 |
4 | 27 |
5 | 30 |
6 | 30 |
7 | 31 |
8 | 37 |
Solution
First quartile (Q1)
Qi= [i * (n + 1) /4] th observation
Q1= [1 * (8 + 1) /4] th observation
Q1 = 2.25th observation
Thus, 2.25th observation lies between the 2nd and 3rd value in the ordered group, between frequency 17 and 26
First quartile (Q1) is calculated as
Q1 = 2nd observation +0.75 * (3rd observation - 2nd observation)
Q1 = 17 + 0.75 * (26 – 17) = 23.75
Third quartile (Q3)
Qi= [i * (n + 1) /4] th observation
Q3= [3 * (8 + 1) /4] th observation
Q3 = 6.75 th observation
So, 6.75 th observation lies between the 6th and 7th value in the ordered group, between frequency 30 and 31
Third quartile (Q3) is calculated as
Q3 = 6th observation +0.25 * (7th observation – 6th observation)
Q3 = 30 + 0.25 * (31 – 30) = 30.25
Now using the quartiles values Q1 and Q3, we will calculate the quartile deviation.
QD = (Q3 - Q1) / 2
QD = (30.25 – 23.75) / 2 = 3.25
Quartile deviation for grouped data
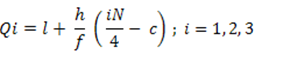
Where,
l = lower boundary of quartile group
h = width of quartile group
f = frequency of quartile group
N = total number of observation
C= cumulative frequency preceding quartile group
Example 3
Age in years | 40 -44 | 45 – 49 | 50 – 54 | 55 - 59 | 60 – 64 | 65 - 69 |
Employees | 5 | 8 | 11 | 10 | 9 | 7 |
Solutions
In the case of Frequency Distribution, Quartiles can be calculated by using the formula:

Class interval | F | Class boundaries | CF |
40 -44 | 5 | 39.5 – 44.5 | 5 |
45 – 49 | 8 | 44.5 – 49.5 | 13 |
50 – 54 | 11 | 49.5 – 54.5 | 24 |
55 – 59 | 10 | 54.5 – 59.5 | 34 |
60 – 64 | 9 | 59.5 – 64.5 | 43 |
65 – 69 | 7 | 64.5 – 69.5 | 50 |
Total | 50 |
|
|
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(50)/4]th observation
Q1 = 12.50th observation
So, 12.50th value is in the interval 44.5 – 49.5
Group of Q1 = 44.5 – 49.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (44.5 + ( 5/ 8)* (1* (50/4) – 5)
Q1 = 49.19
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (50) /4] th observation
Q3 = 37.5th observation
So, 37.5th value is in the interval 59.5 – 64.5
Group of Q3 = 59.5 – 64.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (59.5 + ( 5/ 9)* (3* (50/4) – 34)
Q3 = 61.44
QD = (Q3 - Q1) / 2
QD = (61.44 – 49.19) / 2 = 6.13
Coefficient of Quartile Deviation = (Q3 –Q1) / (Q3 + Q1)
= (61.44 – 49.19) /(61.44 + 49.19) = 0.11
Example 4 – computation of quartile deviation for grouped test scores
Class | Frequency |
9.3-9.7 | 22 |
9.8-10.2 | 55 |
10.3-10.7 | 12 |
10.8-11.2 | 17 |
11.3-11.7 | 14 |
11.8-12.2 | 66 |
12.3-12.7 | 33 |
12.8-13.2 | 11 |
Solution
Class | Frequency | Class boundaries | CF |
9.3-9.7 | 2 | 9.25-9.75 | 2 |
9.8-10.2 | 5 | 9.75-10.25 | 2 + 5 = 7 |
10.3-10.7 | 12 | 10.25-10.75 | 7 + 12 = 19 |
10.8-11.2 | 17 | 10.75-11.25 | 19 + 17 = 36 |
11.3-11.7 | 14 | 11.25-11.75 | 36 + 14 = 50 |
11.8-12.2 | 6 | 11.75-12.25 | 50 + 6 = 56 |
12.3-12.7 | 3 | 12.25-12.75 | 56 + 3 = 59 |
12.8-13.2 | 1 | 12.75-13.25 | 59 + 1 = 60 |
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(60)/4]th observation
Q1 = 15th observation
So, 15th value is in the interval 10.25-10.75
Group of Q1 = 10.25-10.75
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (10.25 + ( 0.5/ 12)* (1* (60/4) – 7)
Q1 = 10.58
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (60) /4] th observation
Q3 = 45th observation
So, 45th value is in the interval 11.25-11.75
Group of Q3 = 11.25-11.75
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (11.25 + ( 0.5/ 14)* (3* (60/4) – 36)
Q3 = 11.57
QD = (Q3 - Q1) / 2
QD = (11.57 – 10.58) / 2 = 0.495
Example 5 – Calculate quartile deviation from the following data
CI | F |
10 – 15 | 6 |
15 – 20 | 10 |
20 – 25 | 15 |
25 – 30 | 22 |
30 – 40 | 12 |
40 – 50 | 9 |
50 – 60 | 4 |
60 - 70 | 2 |
Solution
CI | F | Cf |
10 – 15 | 6 | 6 |
15 – 20 | 10 | 16 |
20 – 25 | 15 | 31 |
25 – 30 | 22 | 53 |
30 – 35 | 12 | 65 |
35 – 40 | 9 | 74 |
45 – 50 | 4 | 78 |
55–60 | 2 | 80 |
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(80)/4]th observation
Q1 = 20th observation
So, 20th value is in the interval 20 - 25
Group of Q1 = 20 - 25
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (20 + ( 5/ 15)* (1* (80/4) – 16)
Q1 = 21.33
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (80) /4] th observation
Q3 = 60th observation
So, 60th value is in the interval 30 - 35
Group of Q3 = 30 - 35
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (30 + ( 5/ 12)* (3* (80/4) – 53)
Q3 = 32.91
QD = (Q3 - Q1) / 2
QD = (32.91 – 21.33) / 2 = 5.79
Merits
- It provides better result than range mode
- It is not affected by extreme values
Demerits
- It is completely dependent on central item
- All items are not taken onto consideration
Mean Deviation:
The average of the absolute values of deviation from the mean, median or mode is called mean deviation. This method removes shortcoming of range and QD.
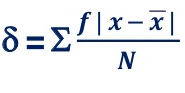
OR
 =
= 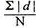
Where, ∑ is total of;
 X is the score, X is the mean, and N is the number of scores
X is the score, X is the mean, and N is the number of scores
D = Deviation of individual scores from mean
Example 1 –
Computation of mean deviation in ungrouped data
X = 55, 45, 39, 41, 40, 48, 42, 53, 41, 56
Solution
X |
| Absolute deviation (signed ignored) |
55 | 55 - 46 = 9 | 9 |
45 | 45 – 46 = -1 | 1 |
39 | -7 | 7 |
41 | -5 | 5 |
40 | -6 | 6 |
48 | 2 | 2 |
42 | -4 | 4 |
53 | 7 | 7 |
41 | -5 | 5 |
56 | 10 | 10 |
∑X = 460 |
|
|
Mean = 460/10 = 46
MD = 56/10 = 5.6
Example 2- Peter did a survey of the number of pets owned by his classmates, with the following result. What is the mean deviation of the number of pets?
No. Of pets | Frequency |
0 | 4 |
1 | 12 |
2 | 8 |
3 | 2 |
4 | 1 |
5 | 2 |
6 | 1 |
Solution
X | F | Fx |
|
|
0 | 4 | 0 | 1.8 | 7.2 |
1 | 12 | 12 | 0.8 | 9.6 |
2 | 8 | 16 | 0.2 | 1.6 |
3 | 2 | 6 | 1.2 | 2.4 |
4 | 1 | 4 | 2.2 | 2.2 |
5 | 2 | 10 | 3.2 | 6.4 |
6 | 1 | 6 | 3.2 | 4.2 |
| 30 | 54 | 4.2 | 33.6 |
Mean = 54/30 = 1.8
MD = 33.6/30 = 1.12
Computation of Mean deviation in grouped data
Example 3 -
Class interval | 15 – 19 | 20 – 24 | 25 – 29 | 30 – 34 | 35 – 39 | 40 – 44 | 45 - 49 |
Frequency | 1 | 4 | 6 | 9 | 5 | 3 | 2 |
Class Interval | F | X | FX | D | FD |
15 – 19 | 1 | 17 | 17 | 15 | 15 |
20 – 24 | 4 | 22 | 88 | 10 | 40 |
25 – 29 | 6 | 27 | 162 | 5 | 30 |
30 - 34 | 9 | 32 | 288 | 0 | 0 |
35 - 39 | 5 | 37 | 185 | 5 | 25 |
40 - 44 | 3 | 42 | 126 | 10 | 30 |
45 - 49 | 2 | 47 | 94 | 15 | 30 |
| N = 30 |
| ∑fx = 960 |
|  |
Mean =960/30 = 32
MD = 170 / 30 = 5.667
Coefficient of mean deviation
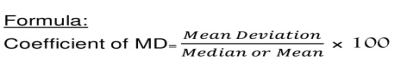
Coefficient of mean deviation = (5.67/32)*100 = 17.71
Example 4 – calculate mean deviation from the median
Class | 5 -15 | 15 - 25 | 25 - 35 | 35 - 45 | 45 – 55 |
Frequency | 5 | 9 | 7 | 3 | 8 |
Solution
x | f | Cf | Mid-point x | x –median | F(x-m) |
5 -15 | 5 | 5 | 10 | 17.42 | 87.1 |
15 -25 | 9 | 14 | 20 | 7.42 | 66.78 |
25 -35 | 7 | 21 | 30 | 2.58 | 18.06 |
35 -45 | 3 | 24 | 40 | 12.58 | 37.74 |
45- 55 | 8 | 32 | 50 | 22.58 | 180.64 |
| 32 |
|
|
| 390.32 |
Since n/2 = 32/2 = 16, therefore the class is 25 – 35 is the median.
Median = 
 Median = 25+16-14 *10 = 27.42
Median = 25+16-14 *10 = 27.42
7
MD from median is 390.32/32 = 12.91
Example 5 –calculate the mean deviation from continuous frequency distribution
Age group | 15 - 25 | 25 - 35 | 35 - 45 | 45 - 55 |
No. Of people | 25 | 54 | 34 | 20 |
Solution
Age group (X) | Number of people (f) | Midpoint x | Fx |
|
|
15 – 25 | 25 | 20 | 500 | 13.684 | 324.1 |
25 – 35 | 54 | 30 | 1620 | 3.684 | 198.936 |
35 – 45 | 34 | 40 | 1360 | 6.316 | 214.744 |
45 - 55 | 20 | 50 | 1000 | 16.316 | 352.32 |
| 133 |
|
|
| 1090.1 |
Mean = 4480/133 = 33.684
MD = 1090.1/133 = 8.196
Merits
- It is easy to calculate
- It helps in making comparison
- It is not affected by extreme items
Demerits
- It ignores algebraic sign. And are not used for mathematical treatment
- It is not reliable
Standard Deviation:
Standard deviation is calculated as square root of average of squared deviations taken from actual mean. It is also called root mean square deviation. This measure suffers from fewer drawbacks and provides accurate results. It removes the drawbacks of ignoring algebraic sign. We square the deviation to make them positive.
Two ways of computing SD
- Direct method
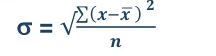
2. Shortcut method
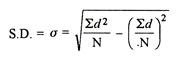
d = Deviation of the score from an assumed mean, say AM; i.e. d = (X – AM). AM is assumed mean
d2 = the square of the deviation.
∑d = the sum of the deviations.
∑d2 = the sum of the squared deviations.
N = No. Of the scores
Standard deviation in ungrouped data
- Direct method
Example 1–
X = 12, 15, 10, 8, 11, 13, 18, 10, 14, 9
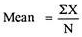
Mean = 120/10 = 12
Scores | d |  |
12 | 12-12 = 0 | 0 |
15 | 15-12 = 3 | 9 |
10 | 10 -12 = -2 | 4 |
8 | -4 | 16 |
11 | -1 | 1 |
13 | 1 | 1 |
18 | 6 | 36 |
10 | -2 | 4 |
14 | 2 | 4 |
9 | -3 | 9 |
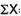 | 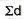 | 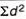 |
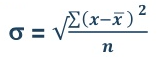
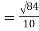 = 2.9
= 2.9
2. Shortcut method
Assumed mean (AM) = 11
Scores | D = (X- AM) | 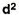 |
12 | 12-11 = 1 | 1 |
15 | 15-11 = 4 | 16 |
10 | 10 -11 = -1 | 1 |
8 | -3 | 9 |
11 | 0 | 0 |
13 | 2 | 4 |
18 | 7 | 49 |
10 | --1 | 1 |
14 | 3 | 9 |
9 | -2 | 4 |
 | 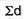 | 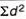 |
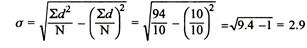
SD from short cut method = 2.9
Example 2 –Ram did a survey of the number of pets owned by his classmates, with the following results
No. Of pets | Frequency |
0 | 4 |
1 | 12 |
2 | 8 |
3 | 2 |
4 | 1 |
5 | 2 |
6 | 1 |
Solution
x | f | Fx |
|
|
|
0 | 4 | 0 | -1.8 | 3.24 | 12.96 |
1 | 12 | 12 | -0.8 | 0.64 | 7.68 |
2 | 8 | 16 | 0.2 | 0.04 | 0.32 |
3 | 2 | 6 | 1.2 | 1.44 | 2.88 |
4 | 1 | 4 | 2.2 | 4.84 | 4.84 |
5 | 2 | 10 | 3.2 | 10.24 | 20.48 |
6 | 1 | 6 | 4.2 | 17.64 | 17.64 |
| 30 | 54 |
|
| 66.80 |
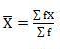
Mean = 54/30 = 1.8

SD = √66.80/30 = 1.49
Standard deviation in grouped data
Direct method
Example 3 –
C.I. | 0 - 2 | 3 - 5 | 6- 8 | 9-11 | 12-14 | 15 -17 | 18 - 20 |
F | 1 | 3 | 5 | 7 | 6 | 5 | 3 |
Solution
C.I | f | Mid-point x | Fx | d | 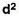 | Fd2 |
0-2 | 1 | 1 | 1 | -10.1 | 102.01 | 102.01 |
3-5 | 3 | 4 | 12 | -7.1 | 50.41 | 151.23 |
6-8 | 5 | 7 | 35 | -4.1 | 16.81 | 84.05 |
9-11 | 7 | 10 | 70 | -1.1 | 1.21 | 8.47 |
12-14 | 6 | 13 | 78 | 1.9 | 3.61 | 21.66 |
15-17 | 5 | 16 | 80 | 4.9 | 24.01 | 120.05 |
18-20 | 3 | 19 | 57 | 7.9 | 62.41 | 187.23 |
| 30 |
| 333 |
|
| 674.70 |
Mean = 333/30 = 11.1
SD =
= 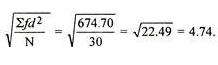
Shortcut method
C.I | f | Mid-point x | d(X-AM) | Fd | Fd2 |
0-2 | 1 | 1 | -9 | -9 | 81 |
3-5 | 3 | 4 | -6 | -18 | 108 |
6-8 | 5 | 7 | -3 | -15 | 45 |
9-11 | 7 | 10 | 0 | 0 | 0 |
12-14 | 6 | 13 | 3 | 18 | 54 |
15-17 | 5 | 16 | 6 | 30 | 180 |
18-20 | 3 | 19 | 9 | 27 | 243 |
| 30 |
|
| 33 | 711 |
Assumed mean = 10
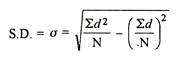
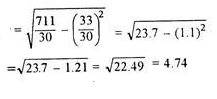
Step deviation method
C.I | f | Mid-point x | d | Fd | Fd2 |
0-2 | 1 | 1 | -3 | -3 | 9 |
3-5 | 3 | 4 | -2 | -6 | 12 |
6-8 | 5 | 7 | -1 | -5 | 5 |
9-11 | 7 | 10 | 0 | 0 | 0 |
12-14 | 6 | 13 | 1 | 6 | 6 |
15-17 | 5 | 16 | 2 | 10 | 20 |
18-20 | 3 | 19 | 3 | 9 | 27 |
| 30 |
|
| 11 | 79 |
Here, d is calculate as (X –AM)/i, where i is length of class interval
d = (1 -10)/3 = -3 and so on
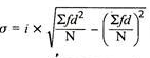

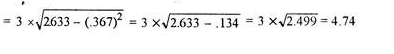
Coefficient of standard deviation
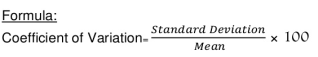
Coefficient of SD = (4.74/11.1)*100 = 42.70
Example 4 – calculate the standard deviation using the direct method
Class interval | Frequency |
30 – 39 | 3 |
40 – 49 | 1 |
50 – 59 | 8 |
60 – 69 | 10 |
70 – 79 | 7 |
80 – 89 | 7 |
90 – 99 | 4 |
Solution
Class interval | Frequency | Mid-point x | Fx |
|
|
|
30 – 39 | 3 | 34.5 | 103.5 | -33.5 | 1122.25 | 3366.75 |
40 – 49 | 1 | 44.5 | 44.5 | -23.5 | 552.25 | 552.25 |
50 – 59 | 8 | 54.5 | 436.0 | -13.5 | 182.25 | 1458 |
60 – 69 | 10 | 64.5 | 645.0 | -3.5 | 12.25 | 122.5 |
70 – 79 | 7 | 74.5 | 521.5 | 6.5 | 42.25 | 295.75 |
80 – 89 | 7 | 84.5 | 591.5 | 16.5 | 272.25 | 1905.75 |
90 – 99 | 4 | 94.5 | 378.0 | 26.5 | 702.25 | 2809 |
| 40 |
| 2720 |
|
| 10510 |
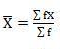
Mean = 2720/40 = 68
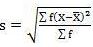
SD = √10510/40 = 16.20
Example 5 - calculate the mean and standard deviation of hours spent watching television by the 220 students.
Hours | No. Of students |
10 – 14 | 2 |
15 – 19 | 12 |
20 – 24 | 23 |
25 – 29 | 60 |
30 – 34 | 77 |
35 – 39 | 38 |
40 - 44 | 8 |
Solution
Hours | No. Of students | x | Fx |
|
|
|
10 – 14 | 2 | 12 | 24 | -17.82 | 317.49 | 634.98 |
15 – 19 | 12 | 17 | 204 | -12.82 | 164.31 | 1971.67 |
20 – 24 | 23 | 22 | 506 | -7.82 | 61.12 | 1405.85 |
25 – 29 | 60 | 27 | 1620 | -2.82 | 7.94 | 476.53 |
30 – 34 | 77 | 32 | 2464 | 2.18 | 4.76 | 366.55 |
35 – 39 | 38 | 37 | 1406 | 7.18 | 51.58 | 1959.98 |
40 - 44 | 8 | 42 | 336 | 12.18 | 148.40 | 1187.17 |
| 220 |
| 6560 |
|
| 8002.73 |
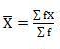
Mean = 6560/220 = 29.82
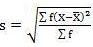
SD = √8002.73/220 = 6.03
Merits
- It takes into account all the items and are used for future statistical analysis
- It is suitable for making comparison
Demerits
It is difficult to compute
Dispersion
Dispersion in statistics is a measure of how distributed the data is meaning it specifies how the values within a data set differ from one another in size. The measures of dispersion determine the spread of data around a measure of location. Measures of dispersion are range and average deviation.
Skewness
Skewness is a measure of asymmetry of distribution about a certain point. Using skewness the measure of asymmetry of a distribution is computed. On the basis of mean, median and mode skewness is measured. Depending on the data points the value of skewness can be positive, negative or undefined.
Difference between skewness and dispersion
Topic | Dispersion | Skewness |
Definition | It measures the tendency of the data set distributed over a range in statistical analysis | It measures the asymmetry in a statistical distribution from the normal distribution |
Measures | It deals with the distribution of values of a set of data around the central point | It studies whether the distribution of values is symmetric or asymmetric |
Calculation | Most common ways to calculate dispersion are range, standard deviation and average deviation | The most common ways to calculate skewness are mean, median, mode |
Variation | It determines the degree of variation in the set of data | It determines the extent of variation in terms of lower and higher values |
Application | It is used for other statistical methods such as regression analysis | It can be used for economical analysis in finance and investing |
Measures of dispersion indicate the scattering of data. It measures the disparity of data from one another.
Range - Range defines the difference between the maximum value and the minimum value given in a data set.
R = H – L
Inter quartile range - the interquartile range measures the range of the middle 50% of the values only. It is calculated as the difference between the upper and lower quartile.
Interquartile range = upper quartile – lower quartile
= Q3 – Q1
Mean deviation - The average of the absolute values of deviation from the mean, median or mode is called mean deviation
Standard deviation - standard deviation is calculated as square root of average of squared deviations taken from actual mean. It is also called root mean square deviation. This measure suffers from less drawbacks and provides accurate results.
For a symmetric distribution the relationship among Q.D., M.D. & S.D. Is:
Q. D. = 2/3 S.D.
M.D. 4/5 =S.D.
Q. D. = 5/6 M.D.
M.D. = 6/5 Q.D.
Q. D.= 2/3 S.D.
S.D. = 3/2 Q. D.
M.D. = 4/5 S.D.
S.D. = 5/4 M.D.
Moments
Moments are a set of statistical parameters to measure a distribution. Four moments are commonly used:
• 1st moment - Mean (describes central value)
• 2nd moment - Variance (describes dispersion)
• 3rd moment - Skewness (describes asymmetry)
• 4th moment - Kurtosis (describes peakedness)
The formula for calculating moments is as follows:
1st moment = 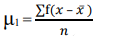
2nd moment =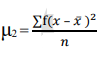
3rd moment = 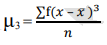
4th moment =
Kurtosis
Kurtosis refers to the degree of peakedness of a frequency curve. It tells how tall and sharp the central peak is, relative to a standard bell curve of a distribution.
Excess Kurtosis
A excess kurtosis compares the kurtosis of a distribution against the kurtosis of a normal distribution. The kurtosis of a normal distribution equals 3. Therefore, the excess kurtosis is found using the formula below:
Excess Kurtosis = Kurtosis – 3
Kurtosis can be described in the following ways:
The types of kurtosis is based on the excess kurtosis of a particular distribution. The excess kurtosis can take positive or negative values, as well as values close to zero.
• Platykurtic– When the kurtosis < 0, shows a negative excess kurtosis, the frequencies throughout the curve are closer to be equal (i.e., the curve is flatter and wider)
• Leptokurtic– When the kurtosis > 0,indicates positive excess kurtosis, there are high frequencies in only a small part of the curve (i.e., the curve is more peaked)

• Mesokurtic- When the kurtosis = 0. Indicates excess kurtosis of zero or close to zero. It refers to the data flows in normal distribution.