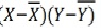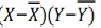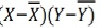4.1 Karl parson’s coefficient of correlation | unit 4 correlation

UNIT – 4

Correlation

4.1 Karl parson’s coefficient of correlation

Karl Pearson’s Coefficient of Correlation is widely used mathematical method is used to calculate the degree and direction of the relationship between linear related variables. The coefficient of correlation is denoted by “r”.

Direct method

Karl Pearson-final

The value of the coefficient of correlation (r) always lies between ±1. Such as:

r=+1, perfect positive correlation

r=-1, perfect negative correlation

r=0, no correlation

Example 1 - Compute Pearson’s coefficient of correlation between advertisement cost and sales as per the data given below:

Advertisement cost	39	65	62	90	82	75	25	98	36	78
sales	47	53	58	86	62	68	60	91	51	84

Solution

X	Y	X - X	(X - X)2	Y - Y	(Y - Y)2
39	47	-26	676	-19	361	494
65	53	0	0	-13	169	0
62	58	-3	9	-8	64	24
90	86	25	625	20	400	500
82	62	17	289	-4	16	-68
75	68	10	100	2	4	20
25	60	-40	1600	-6	36	240
98	91	33	1089	25	625	825
36	51	-29	841	-15	225	435
78	84	13	169	18	324	234
650	660		5398		2224	2704

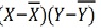
r = (2704)/√5398 √2224 = (2704)/(73.2*47.15) = 0.78

Thus Correlation coefficient is positively correlated

Example 2

Compute correlation coefficient from the following data

Hours of sleep (X)	Test scores (Y)
8	81
8	80
6	75
5	65
7	91
6	80

X	Y	X - X	(X - X)2	Y - Y	(Y - Y)2
8	81	1.3	1.8	2.3	5.4	3.1
8	80	1.3	1.8	1.3	1.8	1.8
6	75	-0.7	0.4	-3.7	13.4	2.4
5	65	-1.7	2.8	-13.7	186.8	22.8
7	91	0.3	0.1	12.3	152.1	4.1
6	80	-0.7	0.4	1.3	1.8	-0.9
40	472		7		361	33

X = 40/6 =6.7

Y = 472/6 = 78.7

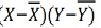
r = (33)/√7 √361 = (33)/(2.64*19) = 0.66

Thus Correlation coefficient is positively correlated

Example 3

Calculate coefficient of correlation between X and Y series using Karl Pearson shortcut method

X	14	12	14	16	16	17	16	15
Y	13	11	10	15	15	9	14	17

Solution

Let assumed mean for X = 15, assumed mean for Y = 14

X	Y	dx	dx2	dy	dy2	dxdy
14	13	-1.0	1.0	-1.0	1.0	1.0
12	11	-3.0	9.0	-3.0	9.0	9.0
14	10	-1.0	1.0	-4.0	16.0	4.0
16	15	1.0	1.0	1.0	1.0	1.0
16	15	1.0	1.0	1.0	1.0	1.0
17	9	2.0	4.0	-5.0	25.0	-10.0
16	14	1	1	0	0	0
15	17	0	0	3	9	0
120	104	0	18	-8	62	6

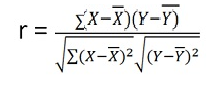
r = 8 *6 – (0)*(-8)

√8*18-(0)2 √8*62 – (-8)2

r = 48/√144*√432 = 0.19

Example 4 - Calculate coefficient of correlation between X and Y series using Karl Pearson shortcut method

X	1800	1900	2000	2100	2200	2300	2400	2500	2600
F	5	5	6	9	7	8	6	8	9

Solution

Assumed mean of X and Y is 2200, 6

X	Y	dx	dx (i=100)	dx2	dy	dy2	dxdy
1800	5	-400	-4	16	-1.0	1.0	4.0
1900	5	-300	-3	9	-1.0	1.0	3.0
2000	6	-200	-2	4	0.0	0.0	0.0
2100	9	-100	-1	1	3.0	9.0	-3.0
2200	7	0	0	0	1.0	1.0	0.0
2300	8	100	1	1	2.0	4.0	2.0
2400	6	200	2	4	0	0	0.0
2500	8	300	3	9	2	4	6.0
2600	9	400	4	16	3	9	12.0

			0	60	9	29	24

Note – we can also proceed dividing x/100

r = (9)(24) – (0)(9)

√9*60-(0)2 √9*29– (9)2

r = 0.69

Example 5 –

X	28	45	40	38	35	33	40	32	36	33
Y	23	34	33	34	30	26	28	31	36	35

Solution

X	Y	X - X	(X - X)2	Y - Y	(Y - Y)2
28	23	-8	64	-8.0	64.0	64.0
45	34	9	81	3.0	9.0	27.0
40	33	4	16	2.0	4.0	8.0
38	34	2	4	3.0	9.0	6.0
35	30	-1	1	-1.0	1.0	1.0
33	26	-3	9	-5.0	25.0	15.0
40	28	4	16	-3	9	-12.0
32	31	-4	16	0	0	0.0
36	36	0	0	5	25	0.0
33	35	-3	9	4	16	-12
360	310	0	216	0	162	97

X = 360/10 = 36

Y = 310/10 = 31

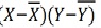
r = 97/(√216 √162 = 0.51

Key Takeaways:

Karl Pearson’s Coefficient of Correlation is widely used mathematical method is used to calculate the degree and direction of the relationship between linear related variables.

The coefficient of correlation is denoted by “r”.

The value of the coefficient of correlation (r) always lies between ±1.

4.2 Probable error and interpretation of coefficient of correlation rank difference method and concurrent deviation method

Definition: The Probable Error of Correlation Coefficient helps in determining the accuracy and reliability of the value of the coefficient that in so far depends on the random sampling.

In other words, the probable error (P.E.) is the value which is added or subtracted from the coefficient of correlation (r) to get the upper limit and the lower limit respectively, within which the value of the correlation expectedly lies.

The probable error of correlation coefficient can be obtained by applying the following formula:

R = coefficient of correlation
N = number of observations

There is no correlation between the variables if the value of ‘r’ is less than P.E. This shows that the coefficient of correlation is not at all significant.

The correlation is said to be certain when the value of ‘r’ is six times more than the probable error; this shows that the value of ‘r’ is significant.

By adding and subtracting the value of P.E from the value of ‘r,’ we get the upper limit and the lower limit, respectively within which the correlation of coefficient is expected to lie. Symbolically, it can be expressed

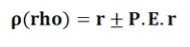
where rho denotes the correlation in a population

The probable Error can be used only when the following three conditions are fulfilled:

The data must approximate to the bell-shaped curve, i.e. a normal frequency curve.

The Probable error computed from the statistical measure must have been taken from the sample.

The sample items must be selected in an unbiased manner and must be independent of each other.

Thus, the probable error is calculated to check the reliability of the value of coefficient calculated from the random sampling.

Key Takeaways:

The probable error (P.E.) is the value which is added or subtracted from the coefficient of correlation (r) to get the upper limit and the lower limit respectively, within which the value of the correlation expectedly lies.

REFERENCES

B.N Gupta – Statistics

S.P Singh – statistics

Gupta and Kapoor – Statistics

Yule and Kendall – Statistics method

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined