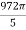UNIT-4
Multivariable Calculus-Differentiation
Limit:
A limit is a number that a function approaches as the independent variable of the function approaches a given value. For example, given the function f (x) = 3x , you could say, “The limit of f (x) as x approaches 2 is 6 .” Symbolically, this is written 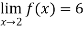 .
.
Continuity:
Continuity is another far-reaching concept in calculus. A function can either be continuous or discontinuous. One easy way to test for the continuity of a function is to see whether the graph of a function can be traced with a pen without lifting the pen from the paper. For the math that we are doing in pre calculus and calculus, a conceptual definition of continuity like this one is probably sufficient, but for higher math, a more technical definition is needed. Using limits, we’ll learn a better and far more precise way of defining continuity as well. With an understanding of the concepts of limits and continuity, you are ready for calculus.
Example 1:
Find the limit of the following points
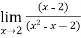
X | 1.9 | 1.99 | 1.999 | 2.001 | 2.01 | 2.1 |
F(x) |
|
|
|
|
|
|
Solution:
We apply the value of each x by finding the respective value through appliying limits
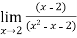
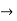 f(x)=
f(x)= 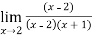
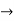 f(x)=
f(x)= 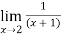
Finding limit at x= 1.9
f(x)= 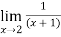
f(1.9)=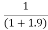
=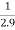
= 0.3448
Limit at x=1.99
f(1.99)= 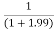
=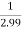
= 0.33444
Limit at x=1.999
f(1.999)= 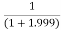
=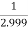
= 0.33344
Limit at x=2.001
f(2.001)= 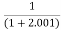
=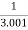
= 0.33322
Limit at x=2.01
f(2.01)= 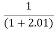
=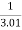
= 0.3225
From the above table we have to estimate the limit when x tends to 2
Here answer is 0.333....
Example 2:
Determine whether the following is dis-continuous at x=-1,0,
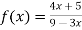
Solution :
Given 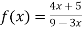
Verifying for continuity at x=-1
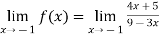
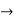
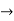
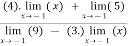
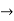
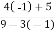
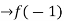
Therefore here 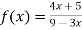 = f(-1)
= f(-1)
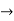 f(x)=f(-1)
f(x)=f(-1)
Hence the function is continuous at x=-1
Verifying at x=0
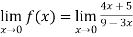
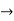
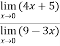
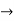
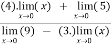
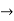
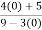
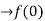
Therefore here 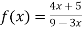 = f(0)
= f(0)
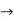 f(x)=f(0)
f(x)=f(0)
Hence the function is continuous at x=0
Example 3:
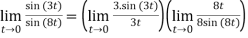
=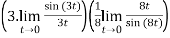
=(3)(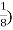
=
Partial Differentiation Partial differentiation is used to differentiate mathematical functions having more than one variable in them. In ordinary differentiation, we find derivative with respect to one variable only, as function contains only one variable. So partial differentiation is more general than ordinary differentiation.
Example 1:
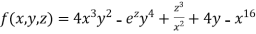
Solution:
Partial derivative for the given equation is,
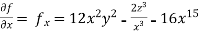
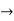
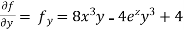
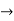
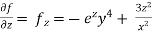
Example 2:
Find the partial derivative of the following
Z=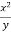 ,x=st , y=
,x=st , y=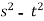
Solution:
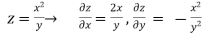
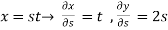
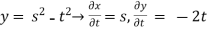
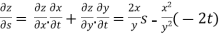
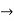
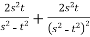 .
.
Example 3:
Solve the following D.E
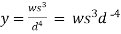
Solution :
Approximating over all change in y
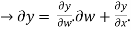
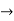
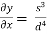 =
=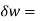 0.02w
0.02w 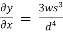 =
=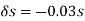
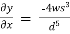 =
=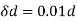
Substituting into equation we get,
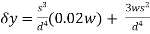 (-0.03s) +
(-0.03s) +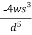 (0.01d) =0.11
(0.01d) =0.11 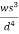
Therefore y decreases by approximately 11 percent.
Total derivative: The total derivative is the derivative with respect to of the function that depends on the variable not only directly but also via the intermediate variables . In mathematics, the total derivative of a function {display style f} at a point is the best linear approximation near this point of the function with respect to its arguments. Unlike partial derivatives, the total derivative approximates the function with respect to all of its arguments, not just a single one.
A(u) = f(x1,x2,.....) and u has continuous partial derivatives fx and fy. Here xi = xi(t) where i=0,1,2,3...n[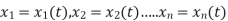 ]
]
Total derivative 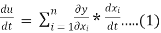
Eq(1) can be written in differential form by eliminating dt as,
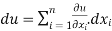
Example 1:
Suppose 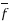 :
: 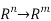 is given by
is given by
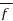 (
(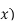 = B
= B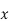 +
+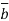 ,
,
Where B is an m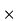 n –matrix and
n –matrix and 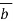
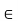
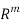 .For example if B=
.For example if B= 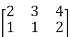 and
and 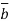 =
= 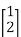
f(x,y,z) = 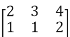
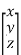 +
+ 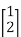 =
= 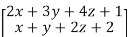
We claim that D.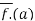 = B for all
= B for all 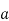 .to check this note
.to check this note
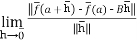
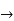
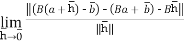
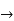
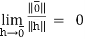
So indeed, D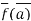 = B
= B
Example 2:
Find the total derivative of f(x,y)=2x+3y with respect to x,
Given that y= sin-1(x)
Solution:
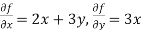
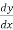 =
= 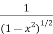
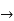
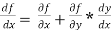
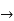 2x+3y+3x.
2x+3y+3x.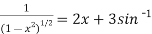 x +
x + 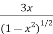
Example 3:
The radius and height of a cylinder are both 2cm.the radius is decreased at 1 cms and the height is increasing at 2 cms. What is the change in volume at this instant
The volume of a right circular cylinder is,
V=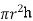
We are taking total derivative of this whole to get,
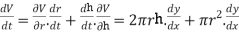
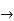 2
2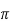 (2)(2)(-1)+
(2)(2)(-1)+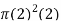 = -8
= -8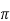 +8
+8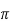 =0
=0
At this moment, the volume of the cylinder is not changing.
Example 1:
Find the normal line to Find the normal line to 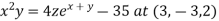
Solution:
We can re-write this equation as:
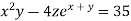
Now we need to find the gradient of the function on the left side as at value (3,-3,2)
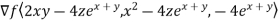
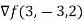 =
= 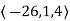
Then the normal plane is,
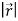 =
=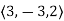 +t
+t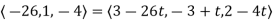
Example 2:
Consider the surface z= 10-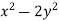 at (1,-1,7), find a 3d tangent vector that points in the direction of steepest ascent.
at (1,-1,7), find a 3d tangent vector that points in the direction of steepest ascent.
Solution:
Let our tangent vector be v= ai+bj+ck.
To find v , we have that,
The direction of steepest ascent of z(x,y) is given by the two-dimensional vector 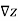 .
.
First we find the x,y components of v,then we find z component of v
Finding x,y components of v,
As the gradient provides the direction of steepest ascent, we compute it:
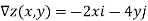
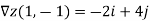
Thus, a=-2 and b=4, and are seeking a tangent vector
V=-2i+4j+ck.
Example 3:
Determine 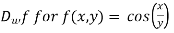 in the direction of
in the direction of 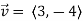
Solution:
First we calculate gradient of the points,
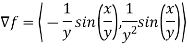
Here we require a unit vector but by our knowledge it is clear that the given vector is not so we change it into unit vector,
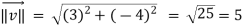
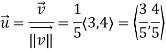
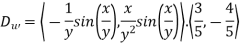
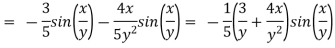
Example 1: Find out the maxima and minima of the function
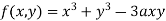
Solution:
Given 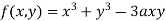 …(i)
…(i)
Partially differentiating (i) with respect to x we get
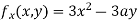 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
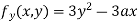 ….(iii)
….(iii)
Now, form the equations 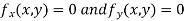
Using (ii) and (iii) we get
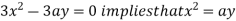
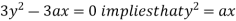
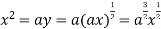 using above two equations
using above two equations
Squaring both side we get
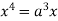
Or 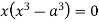
This show that 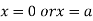
Also we get 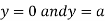
Thus we get the pair of value as 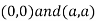
Now, we calculate
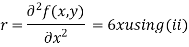
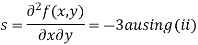
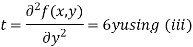
Putting above values in
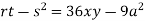
At point (0,0) we get
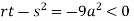
So, the point (0,0) is a saddle point.
At point 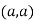 we get
we get
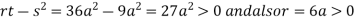
So the point 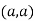 is the minimum point where
is the minimum point where 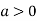
In case 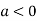
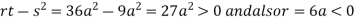
So the point 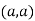 is the maximum point where
is the maximum point where 
Example 2:Find the maximum and minimum point of the function
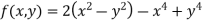
Partially differentiating given equation with respect to and x and y then equate them to zero
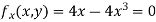
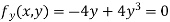
On solving above we get 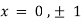
Also 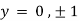
Thus we get the pair of values (0,0), (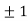 ,0) and (0,
,0) and (0,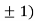
Now, we calculate
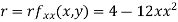
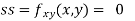
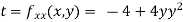
At the point (0,0)
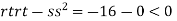
So function has saddle point at (0,0).
At the point (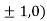
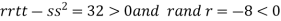
So the function has maxima at this point (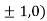 .
.
At the point (0,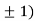
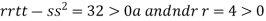
So the function has minima at this point (0,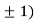 .
.
At the point (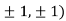
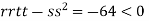
So the function has an saddle point at (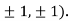
Example 3: Find the maximum and minimum value of 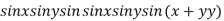
Let 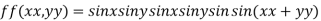
Partially differentiating given function with respect to x and y and equate it to zero
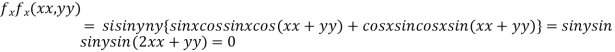 ..(i)
..(i)
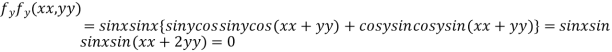 ..(ii)
..(ii)
On solving (i) and (ii) we get
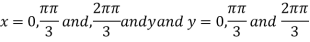
Thus pair of values are 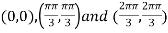
Now, we calculate
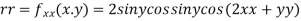
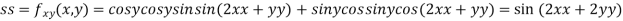
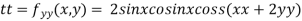
At the point (0,0)
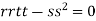
So further investigation is required
On the x axis y = 0 , f(x,0)=0
On the line y=x, 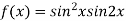
At the point 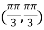
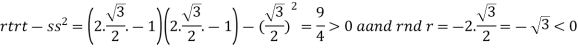
So that the given function has maximum value at 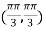
Therefore maximum value of given function
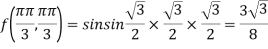
At the point 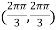
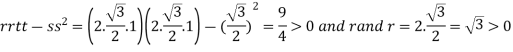
So that the given function has minimum value at 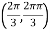
Therefore minimum value of the given function
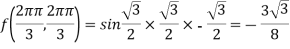
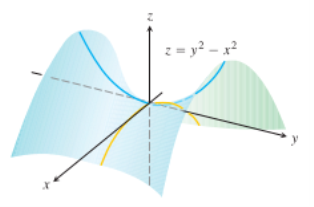
Saddle point: A Differentiable function f(x,y) has a saddle point at a critical point (a,b) if in every open disk centered at (a,b) there are domain points (x,y) where f(x,y)> f(a ,b) and domain points where f(x ,y)<f(a ,b). The corresponding point (a,b,f(a,b)) on the surface z = f(x,y) is called a saddle point of the surface.
Example 4: Find the local extreme values of f (x,y) =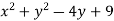
Solution: The domain of f is the entire plane ( so there are no boundary points ) and the partial derivative 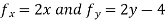 exist everywhere .Therefore ,local extreme values can occur only where
exist everywhere .Therefore ,local extreme values can occur only where
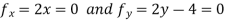
The only possibility is the point (0,2), where the value of f is 5 .Since
f(x,y)=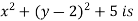 never less than 5 , we see that the critical point (0,2) gives a local minimum.
never less than 5 , we see that the critical point (0,2) gives a local minimum.
Example 5: Find the local extreme values (if any) of f (x,y) =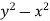
Solution: The domain of f is the entire plane ( so there are no boundary points )and the partial derivatives 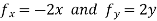 exist everywhere .
exist everywhere .
Therefore local extrema can occur only at the origin (0,0) where 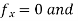
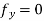
Along the positive x-axis , however , f has the value f(x,0) =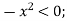
Along the positive y-axis ,f has the value f(0,y) =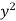 >0
>0
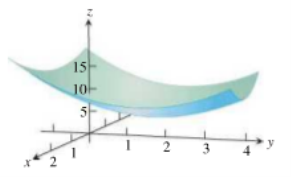
Therefore ,every open disk in the xy-plane centered at (0,0) contains points where the function is positive and points where it is negative . The function has a saddle point at the origin and no local extreme values (see the following figure).
Let 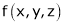 be a function of x, y, z which to be discussed for stationary value.
be a function of x, y, z which to be discussed for stationary value.
Let 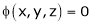 be a relation in x, y, z
be a relation in x, y, z
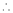 for stationary values we have,
for stationary values we have,
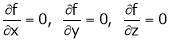
i.e. 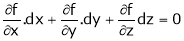 … (1)
… (1)
Also from 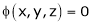 we have
we have
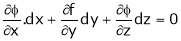 … (2)
… (2)
Let ‘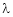 ’ be undetermined multiplier then multiplying equation (2) by
’ be undetermined multiplier then multiplying equation (2) by 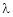 and adding in equation (1) we get,
and adding in equation (1) we get,
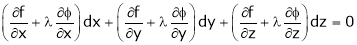
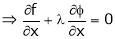 … (3)
… (3)
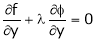 … (4)
… (4)
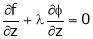 … (5)
… (5)
Solving equation (3), (4) (5) & we get values of x, y, z and 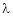 .
.
Example 1: Decampere a positive number ‘a’ in to three parts, so their product is maximum
Solution: Let x, y, z be the three parts of ‘a’ then we get.
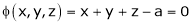 … (1)
… (1)
Here we have to maximize the product
i.e. 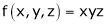
 By Lagrange’s undetermined multiplier, we get,
By Lagrange’s undetermined multiplier, we get,
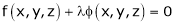
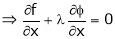 … (2)
… (2)
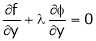 … (3)
… (3)
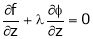 … (4)
… (4)
Ie.
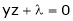 … (2)’
… (2)’
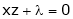 … (3)’
… (3)’
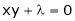 … (4)
… (4)
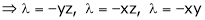
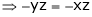
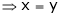
And 
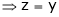
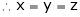
From (1)
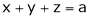
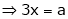
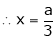
Thus 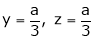 .
.
Hence their maximum product is 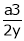 .
.
Example 2: Find the point on plane 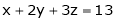 nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
Solution: Let 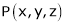 be the point on sphere
be the point on sphere 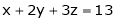 which is nearest to the point
which is nearest to the point 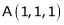 . Then shortest distance.
. Then shortest distance.
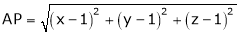
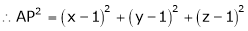
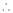 Let
Let 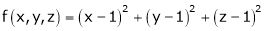
Under the condition 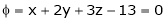 … (1)
… (1)
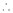 By method of Lagrange’s undetermined multipliers we have
By method of Lagrange’s undetermined multipliers we have
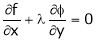
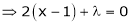 … (2)
… (2)
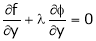
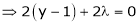 … (3)
… (3)
i.e. 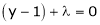 &
&
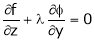
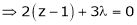 … (4)
… (4)
From (2) we get 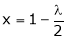
From (3) we get 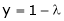
From (4) we get 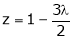
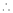 Equation (1) becomes
Equation (1) becomes
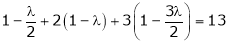
i.e. 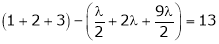
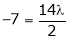
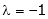
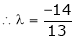
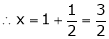
y = 2
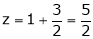
Example 1:Find the gradient of the following:
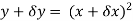
Solution: 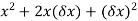
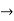
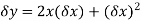
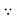 y=
y=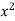
 =
= 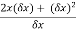 .
.
= 2x+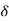
Example 2:
Find the curl of F(x,y,z) = 3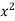 i+2zj-xk
i+2zj-xk
Curl F = 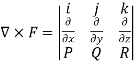
=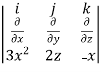
= 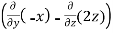 i -
i - 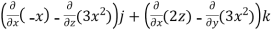
= (0-2)i-(-1-0)j+(0-0)k
= -2i+j
Example 3:
What is the curl of the vector field F= ( x +y +z ,x-y-z,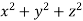 )?
)?
Solution:
Curl F = 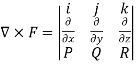
= 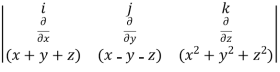
=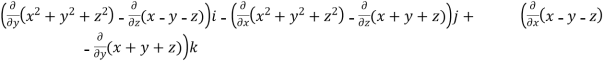
= (2y+1)i-(2x-1)j+(1-1)k
= (2y+1)i+(1-2x)j+0k
= (2y+1, 1-2x,0)
Example 4: Compute 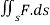 where F= (3x+
where F= (3x+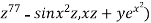 and s is the surface of the box such that 0
and s is the surface of the box such that 0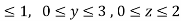 use outward normal n
use outward normal n
Solution: Writing the given vector fields in a suitable manner for finding divergence
Div F =3+2y+x
We use the divergence theorem to convert the surface integral into a triple integral
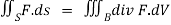
Where B is the box 0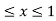 , 0
, 0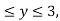
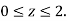
We compute the triple integral of div F=3+2y+x over the box B
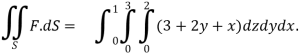
=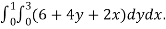
=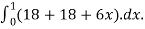
= 36+3=39
Example 5: For F= (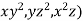 use divergence theorem to evaluate
use divergence theorem to evaluate 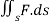 where s is the dphere of radius 3 centered at origin.
where s is the dphere of radius 3 centered at origin.
Solution: Since div F= 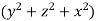 , the surface integral is equal to the triple integral.
, the surface integral is equal to the triple integral.
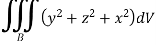
To evaluate the triple integral we can change value of variables to spherical co-ordinates,
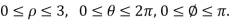
The integral is 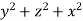 =
=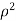 .For spherical co-ordinates, we know that the jacobian determinant is dV =
.For spherical co-ordinates, we know that the jacobian determinant is dV = 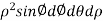 .therefore, the integral is
.therefore, the integral is
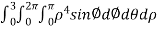 =
= 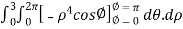
= 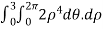
=