UNIT 3

Arrays

3.1   Introduction to Arrays (1-D, 2-D)

One dimensional Array

The variable allows us to store a single value at a time, what if we want to store roll no. Of 100 students? For this task, we have to declare 100 variables, then assign values to each of them. What if there are 10000 students or more? As you can see declaring that many variables for a single entity (i.e student) is not a good idea. In a situation like these arrays provide a better way to store data.

What is an Array?

An array is a collection of one or more values of the same type. Each value is called an element of the array. The elements of the array share the same variable name but each element has its own unique index number (also known as a subscript). An array can be of any type, For example: int, float, char etc. If an array is of type int then it's elements must be of type int only.

To store roll no. Of 100 students, we have to declare an array of size 100 i.e roll_no[100]. Here size of the array is 100 , so it is capable of storing 100 values. In C, index or subscript starts from 0, so roll_no[0] is the first element, roll_no[1] is the second element and so on. Note that the last element of the array will be at roll_no[99] not at roll_no[100] because the index starts at 0.

Arrays can be single or multidimensional. The number of subscript or index determines the dimensions of the array. An array of one dimension is known as a one-dimensional array or 1-D array, while an array of two dimensions is known as a two-dimensional array or 2-D array.

Let's start with a one-dimensional array.

One-dimensional array

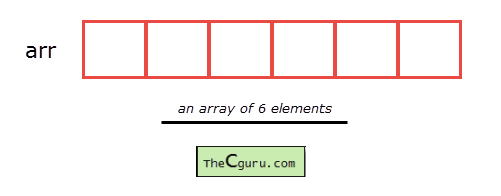
Conceptually you can think of a one-dimensional array as a row, where elements are stored one after another.

Syntax: datatype array_name[size];

Datatype: It denotes the type of the elements in the array.

Array_name: Name of the array. It must be a valid identifier.

Size: Number of elements an array can hold. Here are some example of array declarations:

Num is an array of type int, which can only store 100 elements of type int.
temp is an array of type float, which can only store 20 elements of type float.
ch is an array of type char, which can only store 50 elements of type char.

Note: When an array is declared it contains garbage values.

The individual elements in the array:

We can also use variables and symbolic constants to specify the size of the array.

Note: Until C99 standard, we were not allowed to use variables to specify the size of the array. If you are using a compiler which supports C99 standard, the above code would compile successfully. However, If you're using an older version of C compiler like Turbo C++, then you will get an error.

The use of symbolic constants makes the program maintainable, because later if you want to change the size of the array you need to modify it at once place only i.e in the #define directive.

Accessing elements of an array

The elements of an array can be accessed by specifying array name followed by subscript or index inside square brackets (i.e []). Array subscript or index starts at 0. If the size of an array is 10 then the first element is at index 0, while the last element is at index 9. The first valid subscript (i.e 0) is known as the lower bound, while last valid subscript is known as the upper bound.

Int my_arr[5];

Then elements of this array are;

First element – my_arr[0]
Second element – my_arr[1]
Third element – my_arr[2]
Fourth element – my_arr[3]
Fifth element – my_arr[4]

Array subscript or index can be any expression that yields an integer value. For example:

In the array my_arr, the last element is at my_arr[4], What if you try to access elements beyond the last valid index of the array?

Sure indexes 5, 10 and -1 are not valid but C compiler will not show any error message instead some garbage value will be printed. The C language doesn't check bounds of the array. It is the responsibility of the programmer to check array bounds whenever required.

Processing 1-D arrays

The following program uses for loop to take input and print elements of a 1-D array.

Expected Output:

How it works:

In Line 5, we have declared an array of 5 integers and variable i of type int. Then a for loop is used to enter five elements into an array. In scanf() we have used & operator (also known as the address of operator) on element arr[i] of an array, just like we had done with variables of type int, float, char etc. Line 13 prints "Printing elements of the array" to the console. The second for loop prints all the elements of an array one by one.

The following program prints the sum of elements of an array.

Expected Output:

How it works: The first for loop asks the user to enter five elements into the array. The second for loop reads all the elements of an array one by one and accumulate the sum of all the elements in the variable s. Note that it is necessary to initialize the variable s to 0, otherwise, we will get the wrong answer because of the garbage value of s.

Initializing Array

When an array is declared inside a function the elements of the array have garbage value. If an array is global or static, then its elements are automatically initialized to 0. We can explicitly initialize elements of an array at the time of declaration using the following syntax:

Syntax: datatype array_name[size] = { val1, val2, val3, ..... ValN };

Datatype is the type of elements of an array.

Array_name is the variable name, which must be any valid identifier.

Size is the size of the array.

Val1, val2 ... Are the constants known as initializers. Each value is separated by a comma(,) and then there is a semi-colon (;) after the closing curly brace (}).

Here is are some examples:

While initializing 1-D array it is optional to specify the size of the array, so you can also write the above statements as:

If the number of initializers is less than the specified size then the remaining elements of the array are assigned a value of 0.

Float temp[5] = {12.3, 4.1};

Here the size of temp array is 5 but there are only two initializers. After this initialization the elements of the array are as follows:

Temp[0] is 12.3
temp[1] is 4.1
temp[2] is 0
temp[3] is 0
temp[4] is 0

If the number of initializers is greater than the size of the array then, the compiler will report an error. For example:

Int num[5] = {1, 2, 3, 4, 5, 6, 7, 8} // error

The following program finds the highest and lowest elements in an array.

Expected Output:

How it works: In line 6, first, we have declared and initialized an array of 10 integers. In the next line, we have declared three more variables of type int namely: i, max and min. In line 9, we have assigned the value of the first element of my_arr to max and min. A for loop is used to iterate through all the elements of an array. Inside the for loop, the first if condition (my_arr[i] > max) checks whether the current element is greater than max, if it is, we assign the value of the current element to max.

The second if statement checks whether the value of the current element is smaller than the value of min. If it is, we assign the value of the current element to min. This process continues until there are elements in the array left to iterate.

When the process is finished, max and min variables will have maximum and minimum values respectively.

Two dimensional Array

The two-dimensional array can be defined as an array of arrays. The 2D array is organized as matrices which can be represented as the collection of rows and columns. However, 2D arrays are created to implement a relational database lookalike data structure. It provides ease of holding the bulk of data at once which can be passed to any number of functions wherever required.

Declaration of two dimensional Array in C

The syntax to declare the 2D array is given below.

1. Data_type array_name[rows][columns];  

Consider the following example.

1. Int twodimen[4][3];  

Here, 4 is the number of rows, and 3 is the number of columns.

Initialization of 2D Array in C

In the 1D array, we don't need to specify the size of the array if the declaration and initialization are being done simultaneously. However, this will not work with 2D arrays. We will have to define at least the second dimension of the array. The two-dimensional array can be declared and defined in the following way.

1. Int arr[4][3]={{1,2,3},{2,3,4},{3,4,5},{4,5,6}};  

Two-dimensional array example in C

1. #include<stdio.h>  
2. Int main(){      
3. Int i=0,j=0;    
4. Int arr[4][3]={{1,2,3},{2,3,4},{3,4,5},{4,5,6}};     
5. //traversing 2D array    
6. For(i=0;i<4;i++){    
7. For(j=0;j<3;j++){    
8.   Printf("arr[%d] [%d] = %d \n",i,j,arr[i][j]);    
9. }//end of j    
10. }//end of i    
11. Return 0;  
12. }    

Output

Arr[0][0] = 1

Arr[0][1] = 2

Arr[0][2] = 3

Arr[1][0] = 2

Arr[1][1] = 3

Arr[1][2] = 4

Arr[2][0] = 3

Arr[2][1] = 4

Arr[2][2] = 5

Arr[3][0] = 4

Arr[3][1] = 5

Arr[3][2] = 6

C 2D array example: Storing elements in a matrix and printing it.

1. #include <stdio.h>    
2. Void main ()    
3. {    
4.    Int arr[3][3],i,j;     
5.    For (i=0;i<3;i++)    
6.    {    
7.        For (j=0;j<3;j++)    
8.        {    
9.            Printf("Enter a[%d][%d]: ",i,j);                
10.            Scanf("%d",&arr[i][j]);    
11.        }    
12.    }    
13.    Printf("\n printing the elements ....\n");     
14.    For(i=0;i<3;i++)    
15.    {    
16.        Printf("\n");    
17.        For (j=0;j<3;j++)    
18.        {    
19.            Printf("%d\t",arr[i][j]);    
20.        }    
21.    }    
22. }    

Output

Enter a[0][0]: 56  

Enter a[0][1]: 10  

Enter a[0][2]: 30 

Enter a[1][0]: 34 

Enter a[1][1]: 21

Enter a[1][2]: 34   

Enter a[2][0]: 45

Enter a[2][1]: 56

Enter a[2][2]: 78  

Printing the elements ....

56      10      30 

34      21      34 

45      56      78

3.2   Character arrays and Strings

A string is a collection of characters, stored in an array followed by null ('\0') character. Null character represents the end of string.

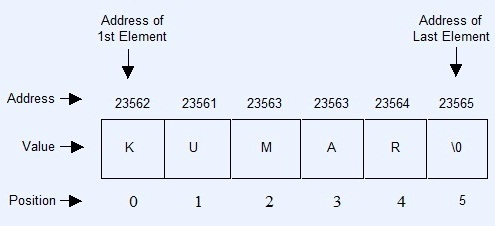
Address of first element is random, address of next element depend upon the type of array. Here, the type is character and character takes one byte in memory, therefore every next address will increment by one.

Index of array will always starts with zero.

Declaration of String or Character array

Declaration of array means creating sequential blocks of memory to hold fixed number of values.

Syntax for string declaration:

Char String-name[size of String ];

Example for string declaration:

Char String [25];    //Statement 1

In the above example we have declared a character array which can hold twenty-five characters at a time.

Initialization of String

Initialization of string means assigning value to declared character array or string.

Examples 1: Using sequence of characters.

Char String [ ] = {'H','e','l','l','o',' ','W','o','r','l','d','\0'};

In the above example, we are declaring and initializing a string at same time. When we declare and initialize a string at same time, giving the size of array is optional and it is programmer's job to specify the null character at the end to terminate the string.

Example 2: Using assignment operator

Char String [ ] = "Hello World";

In this approach, programmer doesn't need to provide null character, compiler will automatically add null character at the end of string.

Input string using getche() function

The getche() read characters from console (output window) one by one and put these characters into string using loop.

Examples for input string with getche() function

#include<stdio.h>

Void main()

{

Char String [50];

Char ch;

Int i;

Printf("\n\n\tEnter your name : ");

For(i=0;i<50;i++)

{

Ch = getche();         //Statement   1

If(ch==13)               //Statement   2

Break;

String [i] = ch;

}

String [i] = '\0';                      //Statement   3

Printf("\n\n\tHello, ");

For(i=0; String [i]!='\0';i++)

Printf("%c", String [i]);

}

Output :

Enter your name : Kumar

Hello Kumar

In the above example, A for loop will execute upto 50 time and getche() which inside for loop will read single character from console and put the character into ch. If user press the enter key, condition given in statement 2 will satisfy and terminate the loop otherwise every character will assign to String. Statement 4 is assigning null character to String.

Input string using scanf() function

The scanf() can read the entire word at a time. The format specifier for a string is "%s". The scanf() ignores the any occurrence of leading whitespace characters and terminate the string at the first occurrence of whitespace after any input.

Examples for input string with scanf() function

#include<stdio.h>

Void main()

{

Char String [50];

Printf("\n\n\tEnter your name : ");

Scanf("%s", String );

Printf("\n\n\tHello %s", String );

}

Output :

Enter your name :      Kumar Wadhwa

Hello Kumar

In the output of above example there is five leading whitespaces in the input which is ignored by the compiler.

Input string using gets() function

The gets() can read the entire line at a time and the string will not terminate until user press the enter key. The gets() will put all the leading and trailing whitespaces into str.

Examples for input string with gets() function

#include<stdio.h>

Void main()

{

Char String [50];

Printf("\n\n\tEnter your name : ");

Gets( String );

Printf("\n\n\tHello %s", String );

}

Output :

Enter your name :      Kumar Wadhwa

Hello      Kumar Wadhwa

In the output of above example there is five leading whitespaces in the input which is not ignored by the compiler.

3.3   Basic Algorithms: Searching, Basic Sorting Algorithms (Bubble, Insertion and Selection)

Searching

Searching is the process of finding some particular element in the list. If the element is present in the list, then the process is called successful and the process returns the location of that element, otherwise the search is called unsuccessful.

There are two popular search methods that are widely used in order to search some item into the list. However, choice of the algorithm depends upon the arrangement of the list.

• Linear Search
• Binary Search

Linear Search

Linear search is the simplest search algorithm and often called sequential search. In this type of searching, we simply traverse the list completely and match each element of the list with the item whose location is to be found. If the match found then location of the item is returned otherwise the algorithm return NULL.

Linear search is mostly used to search an unordered list in which the items are not sorted. The algorithm of linear search is given as follows.

Algorithm

• LINEAR_SEARCH(A, N, VAL)
• Step 1: [INITIALIZE] SET POS = -1
• Step 2: [INITIALIZE] SET I = 1
• Step 3: Repeat Step 4 while I<=N
• Step 4: IF A[I] = VAL
  SET POS = I
  PRINT POS
  Go to Step 6
  [END OF IF]
  SET I = I + 1
  [END OF LOOP]
• Step 5: IF POS = -1
  PRINT " VALUE IS NOT PRESENTIN THE ARRAY "
  [END OF IF]
• Step 6: EXIT

Complexity of algorithm

C Program

1. #include<stdio.h>   
2. Void main ()  
3. {  
4.    Int a[10] = {10, 23, 40, 1, 2, 0, 14, 13, 50, 9};  
5.    Int item, i,flag;  
6.    Printf("\nEnter Item which is to be searched\n");  
7.    Scanf("%d",&item);  
8.    For (i = 0; i< 10; i++)  
9.    {  
10.        If(a[i] == item)   
11.        {  
12.            Flag = i+1;  
13.            Break;  
14.        }   
15.        Else   
16.        Flag = 0;  
17.    }   
18.    If(flag != 0)  
19.    {  
20.        Printf("\nItem found at location %d\n",flag);  
21.    }  
22.    Else  
23.    {  
24.        Printf("\nItem not found\n");   
25.    }  
26. }   

Output:

Enter Item which is to be searched

20

Item not found

Enter Item which is to be searched

23

Item found at location 2

Java Program

1. Import java.util.Scanner;  
2.  
3. Public class Leniear_Search {  
4. Public static void main(String[] args) {  
5.    Int[] arr = {10, 23, 15, 8, 4, 3, 25, 30, 34, 2, 19};  
6.    Int item,flag=0;   
7.    Scanner sc = new Scanner(System.in);  
8.    System.out.println("Enter Item ?");  
9.    Item = sc.nextInt();  
10.    For(int i = 0; i<10; i++)  
11.    {  
12.        If(arr[i]==item)  
13.        {  
14.            Flag = i+1;  
15.            Break;  
16.        }  
17.        Else   
18.            Flag = 0;   
19.    }  
20.    If(flag != 0)  
21.    {  
22.        System.out.println("Item found at location" + flag);  
23.    }  
24.    Else   
25.        System.out.println("Item not found");  
26.      
27. }  
28. }  

Output:

Enter Item ?

23

Item found at location 2

Enter Item ?

22

Item not found

C# Program

1. Using System;  
2.                  
3. Public class LinearSearch  
4. {  
5.    Public static void Main()  
6.    {  
7.        Int item, flag = 0;  
8.        Int[]  a= {10, 23, 5, 90, 89, 34, 12, 34, 1, 78};   
9.        Console.WriteLine("Enter the item value");  
10.        Item = Convert.ToInt32(Console.ReadLine());  
11.        For(int i=0;i<10;i++)  
12.        {  
13.            If(item == a[i])  
14.            {  
15.                Flag = i+1;  
16.                Break;  
17.            }  
18.            Else   
19.                Flag = 0;   
20.        }  
21.        If(flag != 0 )   
22.        {  
23.            Console.WriteLine("Item Found at Location " + flag);  
24.        }  
25.        Else   
26.            Console.WriteLine("Item Not Found");  
27.          
28.    }  
29. }  

Output:

Enter the item value

78

Item Found at Location 10

Enter the item value

22

Item not found

Python Program

1. Arr = [10,2,3,4,23,5,21,45,90,100];  
2. Item = int(input("Enter the item which you want to search "));  
3. For i in range (0,len(arr)):  
4.    If arr[i] == item:  
5.        Flag = i+1;  
6.        Break;  
7.    Else:   
8.        Flag = 0;   
9. If flag != 0:   
10.    Print("Item found at location %d" % (flag));  
11. Else :   
12.    Print("Item not found");  

Output:

Enter the item which you want to search 2

Item found at location 2

Enter the item which you want to search 101

Item not found

Binary Search

Binary search is the search technique which works efficiently on the sorted lists. Hence, in order to search an element into some list by using binary search technique, we must ensure that the list is sorted.

Binary search follows divide and conquer approach in which, the list is divided into two halves and the item is compared with the middle element of the list. If the match is found then, the location of middle element is returned otherwise, we search into either of the halves depending upon the result produced through the match.

Binary search algorithm is given below.

BINARY_SEARCH(A, lower_bound, upper_bound, VAL)

• Step 1: [INITIALIZE] SET BEG = lower_bound
  END = upper_bound, POS = - 1
• Step 2: Repeat Steps 3 and 4 while BEG <=END
• Step 3: SET MID = (BEG + END)/2
• Step 4: IF A[MID] = VAL
  SET POS = MID
  PRINT POS
  Go to Step 6
  ELSE IF A[MID] > VAL
  SET END = MID - 1
  ELSE
  SET BEG = MID + 1
  [END OF IF]
  [END OF LOOP]
• Step 5: IF POS = -1
  PRINT "VALUE IS NOT PRESENT IN THE ARRAY"
  [END OF IF]
• Step 6: EXIT

Complexity

Example

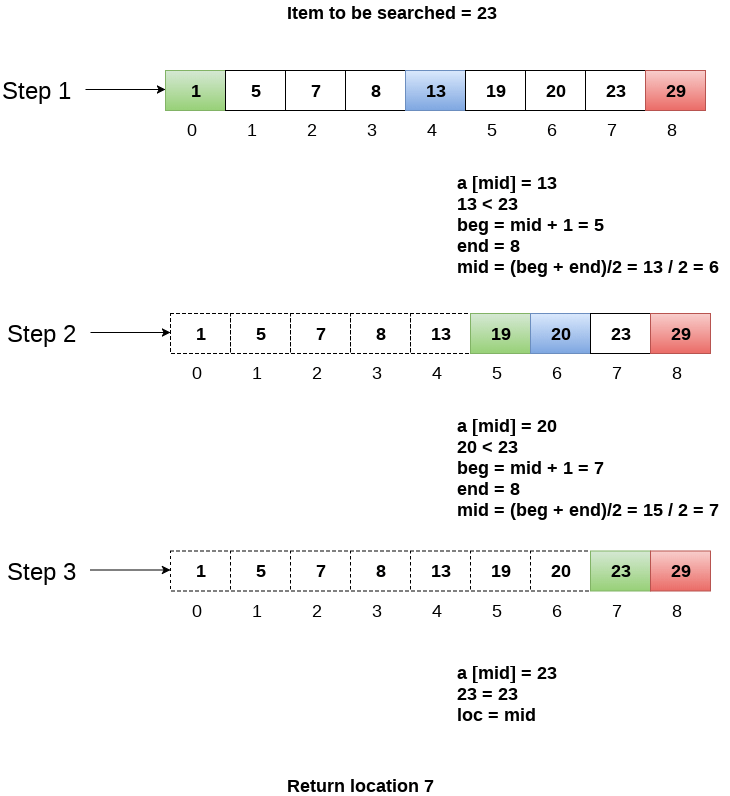
Let us consider an array arr = {1, 5, 7, 8, 13, 19, 20, 23, 29}. Find the location of the item 23 in the array.

In 1st step :

1. BEG = 0   
2. END = 8ron  
3. MID = 4   
4. a[mid] = a[4] = 13 < 23, therefore  

In Second step:

1. Beg = mid +1 = 5   
2. End = 8  
3. Mid = 13/2 = 6    
4. a[mid] = a[6] = 20 < 23, therefore;   

In third step:

1. Beg = mid + 1 = 7   
2. End = 8   
3. Mid = 15/2 = 7  
4. a[mid] = a[7]   
5. a[7] = 23 = item;   
6. Therefore, set location = mid;   
7. The location of the item will be 7.   

Binary Search Program using Recursion

C program

1. #include<stdio.h>  
2. Int binarySearch(int[], int, int, int);  
3. Void main ()  
4. {  
5.    Int arr[10] = {16, 19, 20, 23, 45, 56, 78, 90, 96, 100};  
6.    Int item, location=-1;   
7.    Printf("Enter the item which you want to search ");  
8.    Scanf("%d",&item);  
9.    Location = binarySearch(arr, 0, 9, item);  
10.    If(location != -1)   
11.    {  
12.        Printf("Item found at location %d",location);  
13.    }  
14.    Else  
15.    {  
16.        Printf("Item not found");  
17.    }  
18. }   
19. Int binarySearch(int a[], int beg, int end, int item)  
20. {  
21.    Int mid;  
22.    If(end >= beg)   
23.    {     
24.        Mid = (beg + end)/2;  
25.        If(a[mid] == item)  
26.        {  
27.            Return mid+1;  
28.        }  
29.        Else if(a[mid] < item)   
30.        {  
31.            Return binarySearch(a,mid+1,end,item);  
32.        }  
33.        Else   
34.        {  
35.            Return binarySearch(a,beg,mid-1,item);  
36.        }  
37.      
38.    }  
39.    Return -1;   
40. }  

Output:

Enter the item which you want to search

19

Item found at location 2

Java

1. Import java.util.*;  
2. Public class BinarySearch {  
3. Public static void main(String[] args) {  
4.    Int[] arr = {16, 19, 20, 23, 45, 56, 78, 90, 96, 100};  
5.    Int item, location = -1;  
6.    System.out.println("Enter the item which you want to search");  
7.    Scanner sc = new Scanner(System.in);  
8.    Item = sc.nextInt();  
9.    Location = binarySearch(arr,0,9,item);  
10.    If(location != -1)  
11.    System.out.println("the location of the item is "+location);  
12.    Else   
13.        System.out.println("Item not found");  
14.    }  
15. Public static int binarySearch(int[] a, int beg, int end, int item)  
16. {  
17.    Int mid;  
18.    If(end >= beg)   
19.    {     
20.        Mid = (beg + end)/2;  
21.        If(a[mid] == item)  
22.        {  
23.            Return mid+1;  
24.        }  
25.        Else if(a[mid] < item)   
26.        {  
27.            Return binarySearch(a,mid+1,end,item);  
28.        }  
29.        Else   
30.        {  
31.            Return binarySearch(a,beg,mid-1,item);  
32.        }  
33.      
34.    }  
35.    Return -1;   
36. }  
37. }  

Output:

Enter the item which you want to search

45

The location of the item is 5

C#

1. Using System;  
2.                  
3. Public class LinearSearch  
4. {  
5.    Public static void Main()  
6.    {  
7.    Int[] arr = {16, 19, 20, 23, 45, 56, 78, 90, 96, 100};  
8.    Int location=-1;   
9.    Console.WriteLine("Enter the item which you want to search ");  
10.    Int item = Convert.ToInt32(Console.ReadLine());  
11.    Location = binarySearch(arr, 0, 9, item);  
12.    If(location != -1)   
13.    {  
14.        Console.WriteLine("Item found at location "+ location);  
15.    }  
16.    Else  
17.    {  
18.        Console.WriteLine("Item not found");  
19.    }  
20. }   
21. Public static int binarySearch(int[] a, int beg, int end, int item)  
22. {  
23.    Int mid;  
24.    If(end >= beg)   
25.    {     
26.        Mid = (beg + end)/2;  
27.        If(a[mid] == item)  
28.        {  
29.            Return mid+1;  
30.        }  
31.        Else if(a[mid] < item)   
32.        {  
33.            Return binarySearch(a,mid+1,end,item);  
34.        }  
35.        Else   
36.        {  
37.            Return binarySearch(a,beg,mid-1,item);  
38.        }  
39.      
40.    }  
41.    Return -1;   
42.  
43.    }  
44. }  

Output:

Enter the item which you want to search

20

Item found at location 3

Python

1. Def binarySearch(arr,beg,end,item):  
2.    If end >= beg:  
3.        Mid = int((beg+end)/2)  
4.        If arr[mid] == item :  
5.            Return mid+1  
6.        Elif arr[mid] < item :   
7.            Return binarySearch(arr,mid+1,end,item)  
8.        Else:   
9.            Return binarySearch(arr,beg,mid-1,item)  
10.    Return -1  
11.      
12.  
13. Arr=[16, 19, 20, 23, 45, 56, 78, 90, 96, 100];  
14. Item = int(input("Enter the item which you want to search ?"))  
15. Location = -1;   
16. Location = binarySearch(arr,0,9,item);  
17. If location != -1:   
18.    Print("Item found at location %d" %(location))  
19. Else:   
20.    Print("Item not found")  

Output:

Enter the item which you want to search ?

96

Item found at location 9

Enter the item which you want to search ?

101

Item not found

Binary Search function using Iteration

1. Int binarySearch(int a[], int beg, int end, int item)  
2. {  
3.    Int mid;  
4.    While(end >= beg)   
5.    {     
6.        Mid = (beg + end)/2;  
7.        If(a[mid] == item)  
8.        {  
9.            Return mid+1;  
10.        }  
11.        Else if(a[mid] < item)   
12.        {  
13.            Beg = mid + 1;  
14.        }  
15.        Else   
16.        {  
17.            End = mid - 1;   
18.        }  
19.      
20.    }  
21.    Return -1;   
22. }   

Bubble Sort

In Bubble sort, Each element of the array is compared with its adjacent element. The algorithm processes the list in passes. A list with n elements requires n-1 passes for sorting. Consider an array A of n elements whose elements are to be sorted by using Bubble sort. The algorithm processes like following.

1. In Pass 1, A[0] is compared with A[1], A[1] is compared with A[2], A[2] is compared with A[3] and so on. At the end of pass 1, the largest element of the list is placed at the highest index of the list.
2. In Pass 2, A[0] is compared with A[1], A[1] is compared with A[2] and so on. At the end of Pass 2 the second largest element of the list is placed at the second highest index of the list.
3. In pass n-1, A[0] is compared with A[1], A[1] is compared with A[2] and so on. At the end of this pass. The smallest element of the list is placed at the first index of the list.

Algorithm :

• Step 1: Repeat Step 2 For i = 0 to N-1
• Step 2: Repeat For J = i + 1 to N - I
• Step 3: IF A[J] > A[i]
  SWAP A[J] and A[i]
  [END OF INNER LOOP]
  [END OF OUTER LOOP
• Step 4: EXIT

Complexity

C Program

1. #include<stdio.h>  
2. Void main ()  
3. {  
4.    Int i, j,temp;   
5.    Int a[10] = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};   
6.    For(i = 0; i<10; i++)  
7.    {  
8.        For(j = i+1; j<10; j++)  
9.        {  
10.            If(a[j] > a[i])  
11.            {  
12.                Temp = a[i];  
13.                a[i] = a[j];  
14.                a[j] = temp;   
15.            }   
16.        }   
17.    }   
18.    Printf("Printing Sorted Element List ...\n");  
19.    For(i = 0; i<10; i++)  
20.    {  
21.        Printf("%d\n",a[i]);  
22.    }  
23. }  

Output:

Printing Sorted Element List . . .

7

9

10

12

23

34

34

44

78

101

C++ Program

1. #include<iostream>  
2. Using namespace std;  
3. Int main ()  
4. {  
5.    Int i, j,temp;   
6.    Int a[10] = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};   
7.    For(i = 0; i<10; i++)  
8.    {  
9.        For(j = i+1; j<10; j++)  
10.        {  
11.            If(a[j] < a[i])  
12.            {  
13.                Temp = a[i];  
14.                a[i] = a[j];  
15.                a[j] = temp;   
16.            }   
17.        }   
18.    }   
19.    Cout <<"Printing Sorted Element List ...\n";  
20.    For(i = 0; i<10; i++)  
21.    {  
22.        Cout <<a[i]<<"\n";  
23.    }  
24.    Return 0;  
25. }  

Output:

Printing Sorted Element List ...

7

9

10

12

23

23

34

44

78

101

Java Program

1. Public class BubbleSort {  
2.    Public static void main(String[] args) {  
3.    Int[] a = {10, 9, 7, 101, 23, 44, 12, 78, 34, 23};  
4.    For(int i=0;i<10;i++)  
5.    {  
6.        For (int j=0;j<10;j++)  
7.        {  
8.            If(a[i]<a[j])  
9.            {  
10.                Int temp = a[i];  
11.                a[i]=a[j];  
12.                a[j] = temp;   
13.            }  
14.        }  
15.    }  
16.    System.out.println("Printing Sorted List ...");  
17.    For(int i=0;i<10;i++)  
18.    {  
19.        System.out.println(a[i]);  
20.    }  
21. }  
22. }  

Output:

Printing Sorted List . . .

7

9

10

12

23

34

34

44

78

101

C# Program

1. Using System;  
2.                      
3. Public class Program  
4. {  
5.    Public static void Main()  
6.    {  
7.        Int i, j,temp;   
8.    Int[] a = {10, 9, 7, 101, 23, 44, 12, 78, 34, 23};   
9.    For(i = 0; i<10; i++)  
10.    {  
11.        For(j = i+1; j<10; j++)  
12.        {  
13.            If(a[j] > a[i])  
14.            {  
15.                Temp = a[i];  
16.                a[i] = a[j];  
17.                a[j] = temp;   
18.            }   
19.        }   
20.    }   
21.    Console.WriteLine("Printing Sorted Element List ...\n");  
22.    For(i = 0; i<10; i++)  
23.    {  
24.        Console.WriteLine(a[i]);  
25.    }  
26.    }  
27. }  

Output:

Printing Sorted Element List . . .

7

9

10

12

23

34

34

44

78

101

Python Program

1. a=[10, 9, 7, 101, 23, 44, 12, 78, 34, 23]  
2. For i in range(0,len(a)):  
3.    For j in range(i+1,len(a)):  
4.        If a[j]<a[i]:  
5.            Temp = a[j]  
6.            a[j]=a[i]  
7.            a[i]=temp  
8. Print("Printing Sorted Element List...")  
9. For i in a:   
10.    Print(i)  

Output:

Printing Sorted Element List . . .

7

9

10

12

23

34

34

44

78

101

Rust Program

1. Fn main()  
2. {  
3.    Let mut temp;  
4. Let mut a: [i32; 10] = [10, 9, 7, 101, 23, 44, 12, 78, 34, 23];  
5.    For i in 0..10  
6.    {  
7.        For j in (i+1)..10  
8.        {  
9.            If a[j] < a[i]  
10.            {  
11.                Temp = a[i];  
12.                a[i] = a[j];  
13.                a[j] = temp;   
14.            }  
15.        }   
16.    }   
17.    Println!("Printing Sorted Element List ...\n");  
18.    For i in &a  
19.    {  
20.        Println!("{} ",i);  
21.    }  
22. }  

Output:

Printing Sorted Element List . . .

7

9

10

12

23

34

34

44

78

101

4

JavaScript Program

1. <html>  
2. <head>  
3. <title>   
4. Bubble Sort   
5. </title>   
6. </head>   
7. <body>  
8. <script>   
9.    Var a = [10, 9, 7, 101, 23, 44, 12, 78, 34, 23];  
10.    For(i=0;i<10;i++)  
11.    {  
12.        For (j=0;j<10;j++)  
13.        {  
14.            If(a[i]<a[j])  
15.            {  
16.                 Temp = a[i];  
17.                a[i]=a[j];  
18.                a[j] = temp;   
19.            }  
20.        }  
21.    }  
22.    Txt = "<br>";  
23.    Document.writeln("Printing Sorted Element List ..."+txt);  
24.    For(i=0;i<10;i++)  
25.    {  
26.        Document.writeln(a[i]);  
27.        Document.writeln(txt);  
28.    }  
29.    </script>   
30.    </body>  
31. </html>  

Output:

Printing Sorted Element List ...

7

9

10

12

23

23

34

44

78

101

PHP Program

1. <html>  
2. <head>  
3. <title>Bubble Sort</title>  
4. </head>  
5. <body>  
6. <?php  
7.    $a = array(10, 9, 7, 101, 23, 44, 12, 78, 34, 23);  
8.    For($i=0;$i<10;$i++)  
9.    {  
10.        For ($j=0;$j<10;$j++)  
11.        {  
12.            If($a[$i]<$a[$j])  
13.            {  
14.                 $temp = $a[$i];  
15.                $a[$i]=$a[$j];  
16.                $a[$j] = $temp;   
17.            }  
18.        }  
19.    }  
20.    Echo "Printing Sorted Element List ...\n";  
21.    For($i=0;$i<10;$i++)  
22.    {  
23.        Echo $a[$i];  
24.        Echo "\n";  
25.    }  
26. ?>  
27. </body>  
28. </html>  

Output:

Printing Sorted Element List ...

7

9

10

12

23

23

34

44

78

101

Selection Sort

Selection sort is a simple sorting algorithm. This sorting algorithm is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list.

The smallest element is selected from the unsorted array and swapped with the leftmost element, and that element becomes a part of the sorted array. This process continues moving unsorted array boundary by one element to the right.

This algorithm is not suitable for large data sets as its average and worst case complexities are of Ο(n2), where n is the number of items.

How Selection Sort Works?

Consider the following depicted array as an example.

For the first position in the sorted list, the whole list is scanned sequentially. The first position where 14 is stored presently, we search the whole list and find that 10 is the lowest value.

So we replace 14 with 10. After one iteration 10, which happens to be the minimum value in the list, appears in the first position of the sorted list.

For the second position, where 33 is residing, we start scanning the rest of the list in a linear manner.

We find that 14 is the second lowest value in the list and it should appear at the second place. We swap these values.

After two iterations, two least values are positioned at the beginning in a sorted manner.

The same process is applied to the rest of the items in the array.

Following is a pictorial depiction of the entire sorting process −

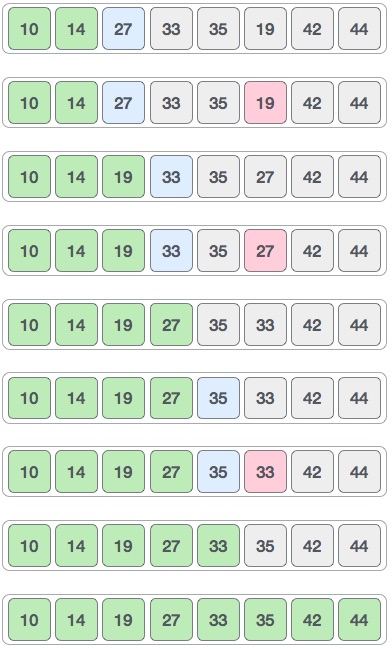
Now, let us learn some programming aspects of selection sort.

Algorithm

Step 1 − Set MIN to location 0

Step 2 − Search the minimum element in the list

Step 3 − Swap with value at location MIN

Step 4 − Increment MIN to point to next element

Step 5 − Repeat until list is sorted

Pseudocode

Procedure selection sort

List  : array of items

n     : size of list

For i = 1 to n - 1

/* set current element as minimum*/

Min = i   

/* check the element to be minimum */

For j = i+1 to n

If list[j] < list[min] then

Min = j;

End if

End for

/* swap the minimum element with the current element*/

If indexMin != i  then

Swap list[min] and list[i]

End if

End for

End procedure

Selection Sort Program

Selection sort is a simple sorting algorithm. This sorting algorithm is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list.

Implementation in C

#include <stdio.h>

#include <stdbool.h>

#define MAX 7

Int intArray[MAX] = {4,6,3,2,1,9,7};

Void printline(int count) {

Int i;

For(i = 0;i < count-1;i++) {

Printf("=");

}

Printf("=\n");

}

Void display() {

Int i;

Printf("[");

// navigate through all items

For(i = 0;i < MAX;i++) {

Printf("%d ", intArray[i]);

}

Printf("]\n");

}

Void selectionSort() {

Int indexMin,i,j;

// loop through all numbers

For(i = 0; i < MAX-1; i++) {

// set current element as minimum

IndexMin = i;

// check the element to be minimum

For(j = i+1;j < MAX;j++) {

If(intArray[j] < intArray[indexMin]) {

IndexMin = j;

}

}

If(indexMin != i) {

Printf("Items swapped: [ %d, %d ]\n" , intArray[i], intArray[indexMin]);

// swap the numbers

Int temp = intArray[indexMin];

IntArray[indexMin] = intArray[i];

IntArray[i] = temp;

}         

Printf("Iteration %d#:",(i+1));

Display();

}

} 

Void main() {

Printf("Input Array: ");

Display();

Printline(50);

SelectionSort();

Printf("Output Array: ");

Display();

Printline(50);

}

If we compile and run the above program, it will produce the following result −

Output

Input Array: [4 6 3 2 1 9 7 ]

==================================================

Items swapped: [ 4, 1 ]

Iteration 1#:[1 6 3 2 4 9 7 ]

Items swapped: [ 6, 2 ]

Iteration 2#:[1 2 3 6 4 9 7 ]

Iteration 3#:[1 2 3 6 4 9 7 ]

Items swapped: [ 6, 4 ]

Iteration 4#:[1 2 3 4 6 9 7 ]

Iteration 5#:[1 2 3 4 6 9 7 ]

Items swapped: [ 9, 7 ]

Iteration 6#:[1 2 3 4 6 7 9 ]

Output Array: [1 2 3 4 6 7 9 ]

==================================================

Insertion Sort

This is an in-place comparison-based sorting algorithm. Here, a sub-list is maintained which is always sorted. For example, the lower part of an array is maintained to be sorted. An element which is to be 'insert'ed in this sorted sub-list, has to find its appropriate place and then it is to be inserted there. Hence the name insertion sort.

Implementation in C

#include <stdio.h>

#include <stdbool.h>

#define MAX 7

Int intArray[MAX] = {4,6,3,2,1,9,7};

Void printline(int count) {

Int i;

For(i = 0;i < count-1;i++) {

Printf("=");

}

Printf("=\n");

}

Void display() {

Int i;

Printf("[");

// navigate through all items

For(i = 0;i < MAX;i++) {

Printf("%d ",intArray[i]);

}

Printf("]\n");

}

Void insertionSort() {

Int valueToInsert;

Int holePosition;

Int i;

// loop through all numbers

For(i = 1; i < MAX; i++) {

// select a value to be inserted.

ValueToInsert = intArray[i];

// select the hole position where number is to be inserted

HolePosition = i;

// check if previous no. Is larger than value to be inserted

While (holePosition > 0 && intArray[holePosition-1] > valueToInsert) {

IntArray[holePosition] = intArray[holePosition-1];

HolePosition--;

Printf(" item moved : %d\n" , intArray[holePosition]);

}

If(holePosition != i) {

Printf(" item inserted : %d, at position : %d\n" , valueToInsert,holePosition);

// insert the number at hole position

IntArray[holePosition] = valueToInsert;

}

Printf("Iteration %d#:",i);

Display();

} 

}

Void main() {

Printf("Input Array: ");

Display();

Printline(50);

InsertionSort();

Printf("Output Array: ");

Display();

Printline(50);

}

If we compile and run the above program, it will produce the following result −

Output

Input Array: [4 6 3 2 1 9 7 ]

==================================================

Iteration 1#:[4 6 3 2 1 9 7 ]

Item moved : 6

Item moved : 4

Item inserted : 3, at position : 0

Iteration 2#:[3 4 6 2 1 9 7 ]

Item moved : 6

Item moved : 4

Item moved : 3

Item inserted : 2, at position : 0

Iteration 3#:[2 3 4 6 1 9 7 ]

Item moved : 6

Item moved : 4

Item moved : 3

Item moved : 2

Item inserted : 1, at position : 0

Iteration 4#:[1 2 3 4 6 9 7 ]

Iteration 5#:[1 2 3 4 6 9 7 ]

Item moved : 9

Item inserted : 7, at position : 5

Iteration 6#:[1 2 3 4 6 7 9 ]

Output Array: [1 2 3 4 6 7 9 ]

==================================================

3.4   Finding roots of equations

The standard form of a quadratic equation is:

Ax2 + bx + c = 0, where

a, b and c are real numbers and

a != 0

The term b2-4ac is known as the discriminant of a quadratic equation. It tells the nature of the roots.

• If the discriminant is greater than 0, the roots are real and different.
• If the discriminant is equal to 0, the roots are real and equal.
• If the discriminant is less than 0, the roots are complex and different.

Program to Find Roots of a Quadratic Equation

#include <math.h>

#include <stdio.h>

Int main() {

Double a, b, c, discriminant, root1, root2, realPart, imagPart;

Printf("Enter coefficients a, b and c: ");

Scanf("%lf %lf %lf", &a, &b, &c);

Discriminant = b * b - 4 * a * c;

// condition for real and different roots

If (discriminant > 0) {

Root1 = (-b + sqrt(discriminant)) / (2 * a);

Root2 = (-b - sqrt(discriminant)) / (2 * a);

Printf("root1 = %.2lf and root2 = %.2lf", root1, root2);

}

// condition for real and equal roots

Else if (discriminant == 0) {

Root1 = root2 = -b / (2 * a);

Printf("root1 = root2 = %.2lf;", root1);

}

// if roots are not real

Else {

RealPart = -b / (2 * a);

ImagPart = sqrt(-discriminant) / (2 * a);

Printf("root1 = %.2lf+%.2lfi and root2 = %.2f-%.2fi", realPart, imagPart, realPart, imagPart);

}

Return 0;

}

Output

Enter coefficients a, b and c: 2.3

4

5.6

Root1 = -0.87+1.30i and root2 = -0.87-1.30i

In this program, the sqrt() library function is used to find the square root of a number.

3.5   Notion of order of complexity through example programs (no formal definition required)

Imagine a classroom of 100 students in which you gave your pen to one person. Now, you want that pen. Here are some ways to find the pen and what the O order is.

O(n2): You go and ask the first person of the class, if he has the pen. Also, you ask this person about other 99 people in the classroom if they have that pen and so on,
This is what we call O(n2).

O(n): Going and asking each student individually is O(N).

O(log n): Now I divide the class into two groups, then ask: “Is it on the left side, or the right side of the classroom?” Then I take that group and divide it into two and ask again, and so on. Repeat the process till you are left with one student who has your pen. This is what you mean by O(log n).

I might need to do the O(n2) search if only one student knows on which student the pen is hidden. I’d use the O(n) if one student had the pen and only they knew it. I’d use the O(log n) search if all the students knew, but would only tell me if I guessed the right side.

NOTE :

We are interested in rate of growth of time with respect to the inputs taken during the program execution .

Another Example

Time Complexity of algorithm/code is not equal to the actual time required to execute a particular code but the number of times a statement executes. We can prove this by using time command. For example, Write code in C/C++ or any other language to find maximum between N numbers, where N varies from 10, 100, 1000, 10000. And compile that code on Linux based operating system (Fedora or Ubuntu) with below command:

Gcc program.c – o program

Run it with time ./program

You will get surprising results i.e. for N = 10 you may get 0.5ms time and for N = 10, 000 you may get 0.2 ms time. Also, you will get different timings on the different machine. So, we can say that actual time requires to execute code is machine dependent (whether you are using pentium1 or pentiun5) and also it considers network load if your machine is in LAN/WAN. Even you will not get the same timings on the same machine for the same code, the reason behind that the current network load.

Now, the question arises if time complexity is not the actual time require executing the code then what is it?
The answer is : Instead of measuring actual time required in executing each statement in the code, we consider how many times each statement execute.
For example:

Output:

Hello World

In above code “Hello World!!!” print only once on a screen. So, time complexity is constant: O(1) i.e. every time constant amount of time require to execute code, no matter which operating system or which machine configurations you are using.
Now consider another code: 

Output:

Hello Word !!!Hello Word !!!Hello Word !!!Hello Word !!!

Hello Word !!!Hello Word !!!Hello Word !!!Hello Word !!!

In above code “Hello World!!!” will print N times. So, time complexity of above code is O(N).

ADDITIONAL INFORMATION :

For example:
Let us consider a model machine which has the following specifications:
–Single processor
–32 bit
–Sequential execution
–1 unit time for arithmetic and logical operations
–1 unit time for assignment and return statements

1.Sum of 2 numbers :

Tsum= 2 = C =O(1)

2.Sum of all elements of a list :

Tsum=1 + 2 * (n+1) + 2 * n + 1 = 4n + 1 =C1 * n + C2 = O(n)

3.Sum of all elements of a matrix :

For this one the complexity is a polynomial equation (quadratic equation for a square matrix)
Matrix nxn => Tsum= an2 +bn + c

For this Tsum if in order of n2 = O(n2)

The above codes do not run in the IDE as they are pseudo codes and do not resemble any programming language .

So from the above, we can conclude that the time of execution increases with the type of operations we make using the inputs.

The above O -> is called Big – Oh which is an asymptotic notation. There are other asymptotic notations like theta and Ohm.

Reference

1. Byron Gottfried, Schaum's Outline of Programming with C, McGraw-Hill.

2. E. Balaguruswamy, Programming in ANSI C, Tata McGraw-Hill

3. Brian W. Kernighan and Dennis M. Ritchie, The C Programming Language, Prentice Hall of India