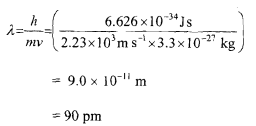Unit -VI

Introduction to quantum theory

6.1 Schrodinger equation & its importance:

The Schrodinger equation is a linear partial differential equation that describes the wave function or state function of a quantum-mechanical system. Schrodinger wave equation is a mathematical expression describing the energy and position of the electron in space and time, taking into account the matter wave nature of the electron inside an atom.

It is based on three considerations. They are;

• Classical plane wave equation,
• Broglie’s Hypothesis of matter-wave, and
• Conservation of Energy.

Classical Plane Wave Equation

A wave is a disturbance of a physical quantity undergoing simple harmonic motion or oscillations about its place. The disturbance gets passed on to its neighbours in a sinusoidal form.

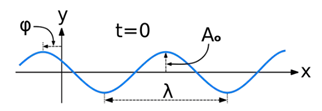
The equation for the wave is a second-order partial differential equation of a scalar variable in terms of one or more space variable and time variable. The one-dimensional wave equation is-

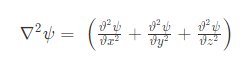
The amplitude (y) for example of a plane progressive sinusoidal wave is given by:

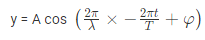
Where, A is the maximum amplitude, T is the period and φ is the phase difference of the wave if any and t is the time in seconds. For a standing wave-

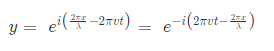
Importance of Schrodinger wave equation:

1. The electronic structure of atoms and molecules can be well explained using the Schrodinger’s equation
2. The solution of Schrodinger’s equation results in quantized properties of systems. E.g.: energy quantization. The quantization is a consequence of the periodic boundary conditions involved.
3. Solving the Schrodinger’s equation for a solid is basically a many-body problem and it involves the solution of complex differential equations. The problem can be solved by expressing the differential Schrodinger’s equation in momentum space/reciprocal space, where the Schrodinger’s equation can be expressed as a set of linear algebraic equations rather than complex differential equations. Those linear equations can be solved using available computational numerical techniques accurately to predict the ground state properties of solids
4. The solution of the Schrodinger’s equation in the reciprocal space gives the electronic band structure of solids.
5. Most of the semiconductor properties such as the origin of energy band gap, the behavior of dopants and their energy levels present in relation to the observed band structure etc., can be well studied by solving the Schrodinger’s equation.
6. Today it is possible to obtain a suitable dopant for a given semiconductor just by solving the corresponding Schrodinger’s equation, without conducting any experiments
7. The materials in practice are impure, they contain various impurities as well as crystalline defects. The ground state properties of these defects can be well studied by solving the Schrodinger’s equation

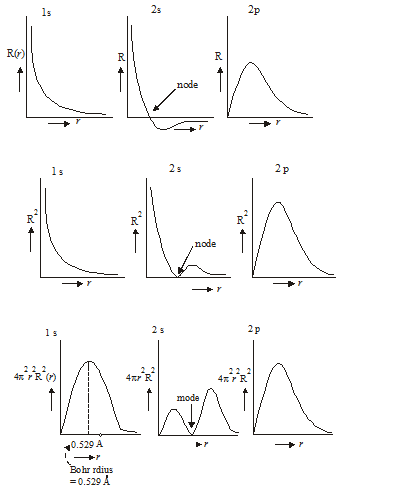
Applications to hydrogen atom:

The wave function of an electron of hydrogen atom is calculated by the help of Schrodinger equation. The interaction between the particles is governed by charges and by the ignorance of electrostatic repulsion.

Time-independent Schrodinger equation:

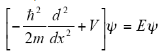
Here,

Total energy  = Kinetic Energy  + Potential energy

In order to attain the kinetic energy for the electron, the equation for centripetal force and coulomb is taken in consideration:

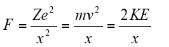
Here,

X= position of electron relative to the proton.

Hence the kinetic energy is given by-

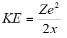
For the potential energy-

Potential Energy = work done to move charge from infinity to the orbital radius

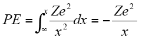
The total energy E is given by

On substituting the values for total and potential energy and on rearrangement:

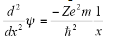
The original wave function is:

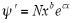
On differentiating the above equation we get-

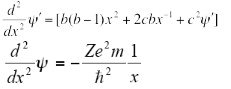
On equating the coefficients we get:

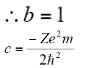
Therefore, the wave function of an electron of a hydrogen atom is:

6.2 Wave mechanical model for many electron atoms‐radial distribution curves:

Electrons race around a central nucleus at such high speeds that they act like waves of energy. As electrons push each other around, the electron orbital clouds form different shapes. Scientists propose that atoms can have up to seven principle energy levels of electrons around the nucleus. This is the electron configuration for the element sulfur, which has 16 electrons.

We and everything around us are made of tiny groups of particles, called atoms. While atoms were once thought to be the smallest unit of matter, they are actually made up of much tinier, high-energy, negatively-charged particles circling at a crazy pace around a nucleus of positive and neutral particles. Since the outer-shell (valence) electrons control the chemical properties of a material, it would be useful to understand how they behave.

One popular theory is the wave-mechanical model, which proposes that electrons are almost as much like a wave of energy as they are like particles. They're moving so fast that they're not really in any one place at any given time, and they keep changing their path in response to the fields around them. In this lesson, we will discuss how scientists use the wave-mechanical model to describe the construction of an atom. The wave-mechanical model was proposed in the 1920s when scientists Erwin Schrödinger and Louis Victor de Broglie determined that the previous model (the Bohr model) was not useful for determining electron locations. The wave-mechanical theory proposes that each electron circling an atom's nucleus occupies a specific orbital and spins a certain direction, but the orbital is like a cloud or wave of energy, not the ring you might imagine thinking about the earth's orbit around the sun.

Developments Leading to Quantum Mechanical Model of Atom Dual Nature of Electron: Matter Waves In 1923 a young French physicist, Louis de Broglie, argued that if light can show a wave as well as a particle nature, why should particles of matter not possess wave like characteristics? He proposed that matter particles should indeed have a wave nature and said that a particle of mass m moving with a velocity v has an associated wavelength, some times called de Broglie wavelength given by the formula;

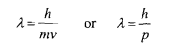
The de Broglie wavelength of a body is inversely proportional to its momentum mv. Since the magnitude of h is very small, the wavelength of the objects of our everyday world would be too small to be observed.

Calculate the de Broglie wavelength associated with a cricket ball weighing 160 g thrown at a speed of 160 km per hour.

Mass of the cricket ball = 160 g = 160 x 10-' kg

= 0.16 kg

Velocity = 160 km/hr

= (160 x 1000)/3600 = 44.44 m s-'

The wavelength associated with the cricket ball will be

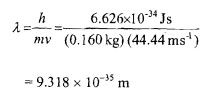
Let us take the velocity of the hydrogen molecule to be equal to its root mean square velocity V, = (~RTIM)"

Substituting the values of R, T and M, we get

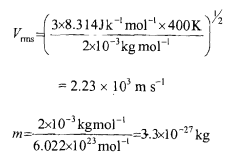
The associated wavelength will be