Unit 3
Principle of virtual work
Concept of virtual work and the principle of virtual work
Principle of Virtual Work and Stability:
The principle of virtual work was proposed by the Swiss mathematician Jean Bernoulli in the eighteenth century. It provides an alternative method for solving problems involving the equilibrium of a particle, a rigid body, or a system of connected rigid bodies.
The definitions of the work of a force and a couple can be presented in terms of the actual movements which are expressed by differential displacements having values of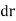 
and
. Consider now an imaginary or virtual movement of a body in static equilibrium, which indicates a displacement or rotation that is assumed and does not actually exist. These movements are first-order differential quantities and will be denoted by the symbols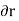 
and 
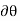(delta r and delta
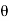),respectively. The virtual work done by a force having a virtualdisplacement 
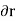is
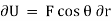
Similarly, when a couple undergoes a virtual rotation
in the plane ofthe couple forces, the virtual work is
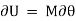
According to the principle of virtual work if a body is in equilibrium, then virtual displacement of the body is zero for all the algebraic sum of the virtual work which is done by all the forces and moments of couple that are acting on the body. Thus,
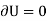
For example, consider the free-body diagram of the particle (ball) that rests on the floor, Fig. Below. If we “imagine” the ball to be displaced downwards a virtual amount 
then the weight does positive virtualwork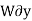
, and the normal force does negative virtual work
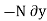,For equilibrium the total virtual work must be zero, so that
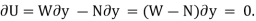
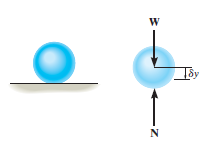
As seen from the above example, no added advantage is gainedby solving particle and rigid-body equilibrium problems using the principle of virtual work. This is because for each application of the virtual-work equation, the virtual displacement, common to every term, factors out, leaving an equation that could have been obtained in a more direct manner by simply applying an equation of equilibrium.
A particle of mass m is acted upon by a number of forces f1,f2….fN Suppose the particle undergoes a virtual displacement 
to reiterate, these impressed forces fi do not cause the particle to move, one imagines it to be incorrectly positioned a little away from the true equilibrium position.
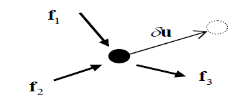
If the particle is moving with an acceleration a, the quantity -mais treated as an inertial force. The total virtual work is then (each term here is the dot product of two vectors)
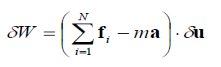
Now if the particle is in equilibrium by the action of the effective (impressed plus inertial) force then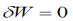 
This can be expressed as follows:
The principle of virtual work (or principle of virtual displacements) if a particle is in equilibrium under the action of a number of forces (including the inertial force) the total work done by the forces for a virtual displacement is zero.
Alternatively, one can define the external virtual work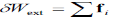 
Wext and the virtual kinetic energy 
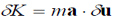in which case the principle takes the form 
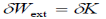(compare with the work-energy principle
In the above, the principle of virtual work was derived using Newton’s second law. One could just as well regard the principle of virtual work as the fundamental principle and from it derives the conditions for equilibrium. In this case one can say that the principle of virtual work (or principle of virtual displacements)
a particle is in equilibrium under the action of a system of forces (including the inertial force) if the total work done by the forces is zero for any virtual displacement of the particle. The term kinematically admissible displacement is used to mean one that does not violate the constraints, and hence one arrives at the version of the principle which is often used in practice:
The principle of virtual work (or principle of virtual displacements): a particle is in equilibrium under the action of a system of forces (including the inertial force) if the total work done by the forces (excluding reaction forces) is zero for any kinematic ally admissible virtual displacement of the particle.
Stable and unstable equilibrium
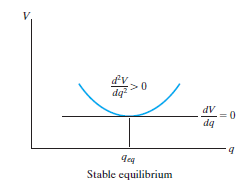
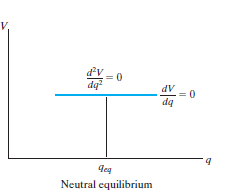
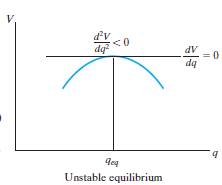
The potential function V of a system can also be used to investigate the stability of the equilibrium configuration, which is classified as stable, neutral, or unstable.
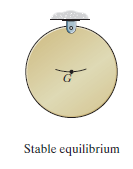
Stable Equilibrium: A system is said to be stable if a system has a tendency to return to its original position when a small displacement is given to the system. The potential energy of the system in this case is at its minimum. A simple example is shown in Fig. Below. When the disk is given a small displacement, its centre of gravity G will always move (rotate) back to its equilibrium position, which is at the lowest point of its path. This is where the potential energy of the disk is at its minimum.
The graph represents stable equilibrium for one degree of freedom system.
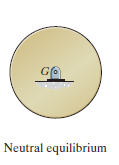
Neutral Equilibrium: A system is said to be in neutral equilibrium if the system still remains in equilibrium when the system is given a small displacement away from its original position. In this case, the potential energy of the system is constant. Neutral equilibrium is shown in Fig. Below, where a disk is pinned at G. Each time the disk is rotated, a new equilibrium position is established and the potential energy remains unchanged.
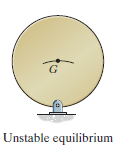
Unstable Equilibrium: A system is said to be unstable if it has a tendency to be displaced further away from its original equilibrium position when it is given a small displacement. The potential energy of the system in this case is a maximum. An unstable equilibrium position of the disk is shown in Fig. Below. Here the disk will rotate away from its equilibrium position when its center of gravity is slightly displaced. At this highest point, its potential energy is at a maximum.
A system is said to be in stable equilibrium if, when displaced from equilibrium, it experiences a net force or torque in a direction opposite to the direction of the displacement. For example, a marble at the bottom of a bowl will experience a restoring force when displaced from its equilibrium position. This force moves it back toward the equilibrium position. Most systems are in stable equilibrium, especially for small displacements. For another example of stable equilibrium, see the pencil in Figure 2.
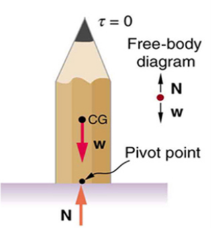
This pencil is in the condition of equilibrium. The net force on the pencil is zero and the total torque about any pivot is zero.
A system is in unstable equilibrium if, when displaced, it experiences a net force or torque in the same direction as the displacement from equilibrium. A system in unstable equilibrium accelerates away from its equilibrium position if displaced even slightly. An obvious example is a ball resting on top of a hill. Once displaced, it accelerates away from the crest. See the next several figures for examples of unstable equilibrium.
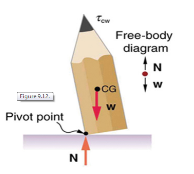
Figure 3If the pencil is displaced slightly to the side (counter clockwise), it is no longer in equilibrium. Its weight produces a clockwise torque that returns the pencil to its equilibrium position.
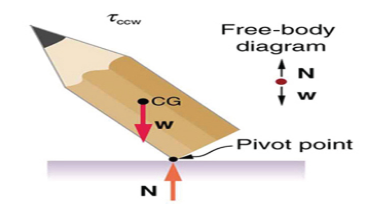
Figure4. If the pencil is displaced too far, the torque caused by its weight changes direction to counter clockwise and causes the displacement to increase.
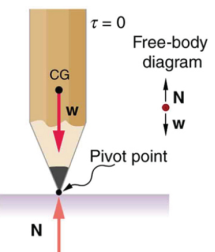
A vertical pencil balanced at its sharp end is shown. The weight of the pencil is acting at its center of gravity and is in the line with the normal reaction N at the pivot point of the pencil.
Figure 5 this figure shows unstable equilibrium, although both conditions for equilibrium are satisfied.
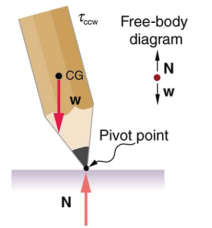
Figure 6 If the pencil is displaced even slightly, a torque is created by its weight that is in the same direction as the displacement, causing the displacement to increase.
A system is in neutral equilibrium if its equilibrium is independent of displacements from its original position. A marble on a flat horizontal surface is an example. Combinations of these situations are possible. For example, a marble on a saddle is stable for displacements toward the front or back of the saddle and unstable for displacements to the side. Figure 6 shows another example of neutral equilibrium.
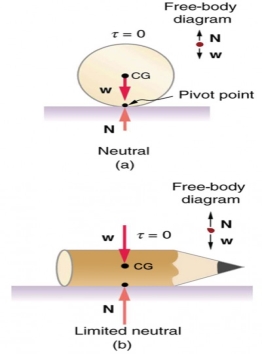
In figure a, a ball is lying on a flat surface and the point of contact with the surface is labelled pivot point. The weight of the ball is acting at the center of gravity of the ball. The normal force N is in the same line as the weight of the ball. The torque on the ball is zero. In figure b, a side view of a pencil lying flat on a table is shown. The sharp end of the pencil is toward right. The weight of the pencil is acting at the center of gravity of the pencil. The normal reaction N of the table surface is in the same line of action as the weight but in the upward direction.
Figure 7 (a) here we see neutral equilibrium. The cg of a sphere on a flat surface lies directly above the point of support, independent of the position on the surface. The sphere is therefore in equilibrium in any location, and if displaced, it will remain put. (b) Because it has a circular cross section, the pencil is in neutral equilibrium for displacements perpendicular to its length.
When we consider how far a system in stable equilibrium can be displaced before it becomes unstable, we find that some systems in stable equilibrium are more stable than others. The pencil in Figure 2 and the person in Figure 8(a) are in stable equilibrium, but become unstable for relatively small displacements to the side. The critical point is reached when the cg is no longer above the base of support. Additionally, since the cg of a person’s body is above the pivots in the hips, displacements must be quickly controlled. This control is a central nervous system function that is developed when we learn to hold our bodies erect as infants. For increased stability while standing, the feet should be spread apart, giving a larger base of support. Stability is also increased by lowering one’s center of gravity by bending the knees, as when a football player prepares to receive a ball or braces themselves for a tackle. A cane, a crutch, or a walker increases the stability of the user, even more as the base of support widens. Usually, the cg of a female is lower (closer to the ground) than a male. Young children have their center of gravity between their shoulders, which increases the challenge of learning to walk.
Introduction to Dynamics:
Kinematics, the part of physics we have studied up to this point, deals with describing motion. We have looked at position, velocity and acceleration as the three basic properties of a particle in motion. In Dynamics, we look at the causes of the motion that we have already studied. In studying these causes, which we shall call forces, we can get a more complete picture of a given physical situation. Starting with a given set of forces, through dynamics we are able to describe all resulting motion. Dynamics is thus the basis for the rest of the study of classical mechanics, and is applied in every branch of physics.
The study of Dynamics begins with an introduction of the concepts of force and mass, then goes on to introduce the basic laws of Dynamics, Newton's Three Laws. From here, we will look at how Newton's Laws are applied to a variety of forces, including tension, friction, and gravity. We will also examine the Dynamics of uniform circular motion.
Studying Newton's Laws is perhaps the most important part of classical mechanics. Kinematics, which you have already studied, lays the groundwork for Newton's laws. For the most part, the subject matter studied after Newton's laws simply applies the laws to a variety of physical situations, and derives further concepts from them. Newton's laws are the axioms of classical mechanics; brilliant not only in their applicability, but in their simplicity.
Kinematics, branch of physics and a subdivision of classical mechanics concerned with the geometrically possible motion of a body or system of bodies without consideration of the forces involved (i.e., causes and effects of the motions).
Kinematics aims to provide a description of the spatial position of bodies or systems of material particles, the rate at which the particles are moving (velocity), and the rate at which their velocity is changing (acceleration). When the causative forces are disregarded, motion descriptions are possible only for particles having constrained motion—i.e., moving on determinate paths. In unconstrained, or free, motion, the forces determine the shape of the path.
When a particle moves on a curved path, a description of its position becomes more complicated and requires two or three dimensions. In such cases continuous descriptions in the form of a single graph or mathematical formula are not feasible. The position of a particle moving on a circle, for example, can be described by a rotating radius of the circle, like the spoke of a wheel with one end fixed at the centre of the circle and the other end attached to the particle. The rotating radius is known as a position vector for the particle, and, if the angle between it and a fixed radius is known as a function of time, the magnitude of the velocity and acceleration of the particle can be calculated. Velocity and acceleration, however, have direction as well as magnitude; velocity is always tangent to the path, while acceleration has two components, one tangent to the path and the other perpendicular to the tangent.
Kinetics, branch of classical mechanics that concerns the effect of forces and torques on the motion of bodies having mass. Authors using the term kinetics apply the nearly synonymous name dynamics (q.v.) to the classical mechanics of moving bodies. This is in contrast to statics, which concerns bodies at rest, under equilibrium conditions. They include under dynamics both kinetics and kinematics (the description of motion in terms of position, velocity, and acceleration, apart from the influence of forces, torques, and masses). Authors not using the term kinetics divide classical mechanics into kinematics and dynamics, including statics as a special case of dynamics in which the sum of the forces and the sum of the torques are both zero.
Rectilinear translation:
Kinematics of rectilinear motion – displacement, velocity, acceleration,
Rectilinear motion
Motion is one of the most common phenomena we come across in our daily lives. For example, a moving car, a kid running on the road or a fly moving in the air are all said to be in motion. So, in general terms, a body is said to be in motion if it changes its position with respect to a reference point and time. Depending upon the path taken by the particle the motion can be of different types like projectile motion, rectilinear motion, rotational motion, etc. For now, we will only focus on the rectilinear motion which is also known as linear motion.
When we require only one co-ordinate axis along with time to describe the motion of a particle it is said to be in linear motion or rectilinear motion. Some examples of linear motion are a parade of soldiers, a train moving along a straight line, and many more.
Distance and Displacement
So now that we have learned about linear motion we will discuss two terms related to change in position. These are called – ‘Distance’ and ‘Displacement’.
Distance is defined as, The total path length covered during a journey While displacement is defined as, The path length from final position of the particle to the origin O. Consider the following figure:
We have an origin O, measurements to the right of O are taken as a positive while to the left are taken as negative. Suppose a person who starts from origin O reaches point A,
Distance = OA
Displacement = OA
Now he turns and reaches point B,
Distance = OA + AB
Displacement = -OB
As we can see, displacement is negative since it is measured to the left of the origin. From the above example, we can infer that distance is always positive while displacement can either be positive or negative.
Speed and Velocity
These terms are used to describe the rate of change of position. Speed is the rate of change of distance while velocity is the rate of change of displacement. Comparing from above as distance can never be negative so the speed is never negative while velocity can be both positive and negative. In mathematical terms, these are defined as follows:
Speed = Distance Travelled Time Taken
Velocity = (Final position–Initial position) Time Taken
Examples for Rectilinear Motion
Following are the rectilinear motion examples:
- The use of elevators in public places is an example of rectilinear motion.
- Gravitational forces acting on objects resulting in free fall is an example of rectilinear motion.
- Kids sliding down from a slide are a rectilinear motion.
- The motion of planes in the sky is a rectilinear motion.
Curvilinear motion
Curvilinear motion is defined as motion that occurs when a particle travels along a curved path. The curved path can be in two dimensions (in a plane), or in three dimensions. This type of motion is more complex than rectilinear (straight-line) motion.
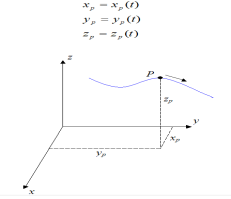
Three-dimensional curvilinear motion describes the most general case of motion for a particle. To find the velocity and acceleration of a particle experiencing curvilinear motion one only needs to know the position of the particle as a function of time.
Let’s say we are given the position of a particle P in three-dimensional Cartesian (x,y,z) coordinates, with respect to time, where
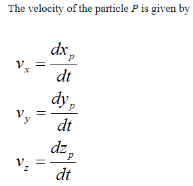
The acceleration of the particle P is given by
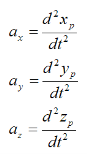
As you can see, if we know the position of a particle as a function of time, it is a fairly simple exercise to find the velocity and acceleration. You simply take the first derivative to find the velocity and the second derivative to find the acceleration.
The magnitude of the velocity of particle P is given by
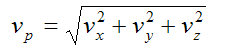
The magnitude of the acceleration of particle P is given by
Note that the direction of velocity of the particle P is always tangent to the curve (i.e. the path travelled, denoted by the blue curve in the figure above). But the direction of acceleration is generally not tangent to the curve.
However, the acceleration component tangent to the curve is equal to the time derivative of the magnitude of velocity of the particle P (along the curve). In other words, if vt is the magnitude of the particle velocity (tangent to the curve), the acceleration component of the particle tangent to the curve (at) is simply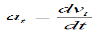
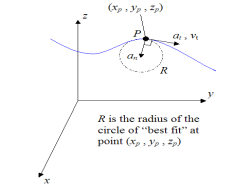
In addition, the acceleration component normal to the curve (an) is given by
Where R is the radius of curvature of the curve at a given point on the curve (xp,yp,zp).
The figure below illustrates the acceleration components at and an at a given point on the curve (xp,yp,zp).
For the specific case where the path of the blue curve is given by y = f(x) (two-dimensional motion), the radius of curvature R is given by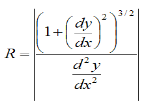
where |x| means the “absolute value” of x. For example, |-2.5| = 2.5, and |3.1| =3.1.
However, it is usually not necessary to know the radius of curvature R along a curve. But nonetheless, it is informative to understand it on the basis of its relationship to the normal acceleration (an).
Alembert’s principle in rectilinear translation and its applications
The principle of virtual work states that the sum of the incremental virtual works done by all external forces Fi acting in conjunction with virtual displacements si of the point on which the associated force is acting is zero:
This technique is useful for solving statics problems, with static forces of constraint. A static force of constraint is one that does no work on the system of interest, but merely holds a certain part of the system in place. In a statics problem there are no accelerations. We can extend the principle of virtual work to dynamics problems, i.e., ones in which real motions and accelerations occur, by introducing the concept of inertial forces. For each parcel of matter in the system with mass m, Newton’s second law states that
F=ma:
We can make this dynamics problem look like a statics problem by defining an inertial force
F* = - ma
And rewriting equation (1.1.2) as
F total = F + F* = 0
Alembert’s principle is just the principle of virtual work with the inertial forces added to the list of forces that do work:
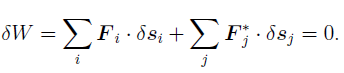
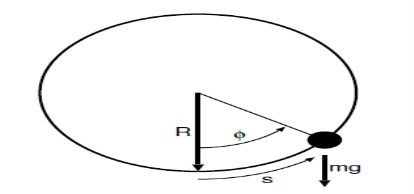
Figure 1.1.1: Sketch of bead of mass m sliding frictionless on a vertical hoop of radius R under the influence of gravity.
Mass falling under gravity
A trivial example would be a mass m falling under the effect of a constant gravitational field g. With z positive upward, the force on the mass is -mg and the work due to this force under vertical displacement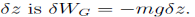 
The inertial force is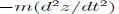 
and the work is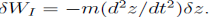 
Setting the sum of the two to zero gives us
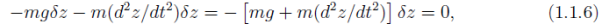
From which we infer the expected result
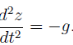
Alembert’s principle offers no advantages over normal procedures in this case. However, it becomes more economical in problems with constraints.
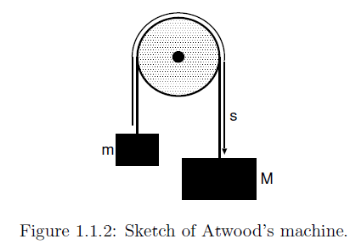
Bead on frictionless vertical hoop
Figure 1.1.1 illustrates the slightly more interesting problem of a bead sliding frictionless around a vertically oriented hoop of wire. Here the force of gravity is not in the direction of motion. The component of gravity normal to the hoop does no work on the bead. Nor does the force of the hoop on the bead that constrains the bead to move in a circle. The work on the bead due to gravity for a small displacement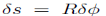 
along the wire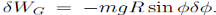 
The acceleration of the bead also has two components, a radial component
Where the tangential velocity is 
and a tangential component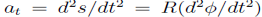 
The radial component of the inertial force mv2=R does no work. However, the tangential component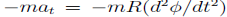 
Does: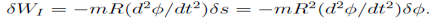
Alembert’s principle thus gives us
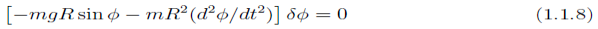
From which we get the governing equation
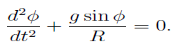
Simple harmonic motion
Simple Harmonic Motion or SHM is defined as a motion in which the restoring force is directly proportional to the displacement of the body from its mean position. The direction of this restoring force is always towards the mean position. The acceleration of a particle executing simple harmonic motion is given by, a(t) = -ω2 x(t). Here, ω is the angular velocity of the particle.
Simple harmonic motion can be described as an oscillatory motion in which the acceleration of the particle at any position is directly proportional to the displacement from the mean position. It is a special case of oscillatory motion.
All the Simple Harmonic Motions are oscillatory and also periodic but not all oscillatory motions are SHM. Oscillatory motion is also called the harmonic motion of all the oscillatory motions wherein the most important one is simple harmonic motion (SHM).
In this type of oscillatory motion displacement, velocity and acceleration and force vary (w.r.t time) in a way that can be described by either sine (or) the cosine functions collectively called sinusoids.
Difference between Periodic, Oscillation and Simple Harmonic Motion
Periodic Motion
- A motion repeats itself after an equal interval of time. For example, uniform circular motion.
- There is no equilibrium position.
- There is no restoring force.
- There is no stable equilibrium position.
Oscillation Motion
- To and fro motion of a particle about a mean position is called an oscillatory motion in which a particle moves on either side of equilibrium (or) mean position is an oscillatory motion.
- It is a kind of periodic motion bounded between two extreme points. For example, Oscillation of Simple Pendulum, Spring-Mass System.
- The object will keep on moving between two extreme points about a fixed point is called mean position (or) equilibrium position along any path. (the path is not a constraint).
- There will be a restoring force directed towards equilibrium position (or) mean position.
- In an oscillatory motion, the net force on the particle is zero at the mean position.
- The mean position is a stable equilibrium position.
Simple Harmonic Motion or SHM
- It is a special case of oscillation along with straight line between the two extreme points (the path of SHM is a constraint).
- Path of the object needs to be a straight line.
- There will be a restoring force directed towards equilibrium position (or) mean position.
- Mean position in Simple harmonic motion is a stable equilibrium.
Types of Simple Harmonic Motion
SHM or Simple Harmonic Motion can be classified into two types,
- Linear SHM
- Angular SHM
Linear Simple Harmonic Motion
When a particle moves to and fro about a fixed point (called equilibrium position) along with a straight line then its motion is called linear Simple Harmonic Motion.
For Example: spring-mass system
Conditions for Linear SHM:
The restoring force or acceleration acting on the particle should always be proportional to the displacement of the particle and directed towards the equilibrium position.
Angular Simple Harmonic Motion
When a system oscillates angular long with respect to a fixed axis then its motion is called angular simple harmonic motion.
Conditions to Execute Angular SHM:
The restoring torque (or) Angular acceleration acting on the particle should always be proportional to the angular displacement of the particle and directed towards the equilibrium position.
Τα–θ or αθ– Τ
Where,
- Τ – Torque
- α angular acceleration
- θ– angular displacement
Mean Position
The point at which net force acting on the particle is zero.
From the mean position, the force acting on the particle is,
The force acting on the particle is negative of the displacement. So this point of equilibrium will be a stable equilibrium.
Amplitude in SHM
It is the maximum displacement of the particle from the mean position.
Time Period and Frequency of SHM
The minimum time after which the particle keeps on repeating its motion is known as the time period (or) the shortest time taken to complete one oscillation is also defined as the time period.
T = 2π\ω
Frequency: The number of oscillations per second is defined as the frequency.
Frequency = 1/T and, angular frequency ω = 2πf = 2π/T
Phase in SHM
The phase of a vibrating particle at any instant is the state of the vibrating (or) oscillating particle regarding its displacement and direction of vibration at that particular instant.
The expression, position of a particle as a function of time.
x = A sin (ωt + Φ)
Where (ωt + Φ) is the phase of the particle, the phase angle at time t = 0 is known as the initial phase.
Phase Difference
The difference of total phase angles of two particles executing simple harmonic motion with respect to the mean position is known as the phase difference. Two vibrating particles are said to be in the same phase, the phase difference between them is an even multiple of π.
Δd = Rnπ where n = 0, 1, 2, 3….
Two vibrating particles are said to be in opposite phase if the phase difference between them is an odd multiple of π.
ΔΦ = (2n + 1) π where n = 0, 1, 2, 3….
Simple Harmonic Motion Equation and its Solution
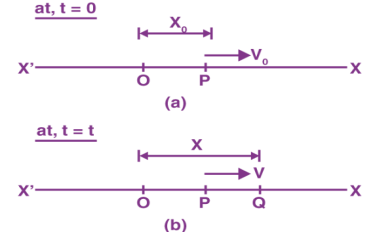
Consider a particle of mass (m) executing Simple Harmonic Motion along a path x o x; the mean position at O. Let the speed of the particle be v0 when it is at position p (at a distance no from O)
At t = 0 the particle at P(moving towards the right)
At t = t the particle is at Q(at a distance x from O)
With a velocity (v)
Solutions of Differential Equations of SHM
The differential equation for the Simple harmonic motion has the following solutions:
These solutions can be verified by substituting this x values in the above differential equation for the linear simple harmonic motion.
Momentum and impulse
What is momentum?
Momentum is a word that we hear used colloquially in everyday life. We are often told that sports teams and political candidates have "a lot of momentum". In this context, the speaker usually means to imply that the team or candidate has had a lot of recent success and that it would be difficult for an opponent to change their trajectory. This is also the essence of the meaning in physics, though in physics we need to be much more precise.
Momentum is a measurement of mass in motion: how much mass is in how much motion. It is usually given the symbol p.
By definition
p=m⋅v
Where m is the mass and v is the velocity. The standard units for momentum are kg.m/s and momentum is always a vector quantity. This simple relationship means that doubling either the mass or velocity of an object will simply double the momentum.
The useful thing about momentum is its relationship to force. You might recall from the kinematic equations that change in velocity
Δv can also be written as aa⋅Δt
We can then see that any change in momentum following an acceleration can be
Δp=m⋅Δv
=m⋅a⋅Δt
=F⋅Δt
What is impulse?
Impulse is a term that quantifies the overall effect of force acting over time. It is conventionally given the symbol J, end text and expressed in Newton-seconds.
For a constant force,
J=F⋅Δt
As we saw earlier, this is exactly equivalent to a change in momentum ∆p. This equivalence is known as the impulse-momentum theorem. Because of the impulse-momentum theorem, we can make a direct connection between how a force acts on an object over time and the motion of the object.
One of the reasons why impulse is important and useful is that in the real world, forces are often not constant. Forces due to things like people and engines tend to build up from zero over time and may vary depending on many factors. Working out the overall effect of all these forces directly would be quite difficult.
When we calculate impulse, we are multiplying force by time. This is equivalent to finding the area under a force-time curve. This is useful because the area can just as easily be found for a complicated shape—variable force—as for a simple rectangle—constant force. It is only the overall net impulse that matters for understanding the motion of an object following an impulse. The concept of impulse that is both external and internal to a system is also fundamental to understanding conservation of momentum.
Work and energy
Energy is a word which tends to be used a lot in everyday life. Though it is often used quite loosely, it does have a very specific physical meaning.
Energy is a measurement of the ability of something to do work. It is not a material substance. Energy can be stored and measured in many forms.
Although we often hear people talking about energy consumption, energy is never really destroyed. It is just transferred from one form to another, doing work in the process. Some forms of energy are less useful to us than others—for example, low level heat energy. It is better to talk about the consumption or extraction of energy resources, for example coal, oil, or wind, than consumption of energy itself.
A speeding bullet has a measurable amount of energy associated with it; this is known as kinetic energy. The bullet gained this energy because work was done on it by a charge of gunpowder which lost some chemical potential energy in the process.
A hot cup of coffee has a measurable amount of thermal energy which it acquired via work done by a microwave oven, which in turn took electrical energy from the electrical grid.
In practice, whenever work is done to move energy from one form to another, there is always some loss to other forms of energy such as heat and sound. For example, a traditional light bulb is only about 3% efficient at converting electrical energy to visible light, while a human being is about 25% efficient at converting chemical energy from food into work.
How do we measure energy and work?
The standard unit used to measure energy and work done in physics is the joule, which has the symbol J. In mechanics, 1 joule is the energy transferred when a force of 1 Newton is applied to an object and moves it through a distance of 1 meter.
Another unit of energy you may have come across is the Calorie. The amount of energy in an item of food is often written in Calories on the back of the packet. A typical 60 gram chocolate bar for example contains about 280 Calories of energy. One Calorie is the amount of energy required to raise 1 kg of water by 1∘degrees Celsius. This is equal to 4184 joules per Calorie, so one chocolate bar has 1.17 million joules or 1.17 MJ of stored energy.
Conservation of energy
In physics, the term conservation refers to something which doesn't change. This means that the variable in an equation which represents a conserved quantity is constant over time. It has the same value both before and after an event.
There are many conserved quantities in physics. They are often remarkably useful for making predictions in what would otherwise be very complicated situations. In mechanics, there are three fundamental quantities which are conserved. These are energy, momentum and angular momentum.
If you have looked at examples in other articles—for example, the kinetic energy of charging elephants—then it may surprise you that energy is a conserved quantity. After all, energy often changes in collisions. It turns out that there are a couple of key qualifying statements we need to add:
- Energy, as we'll be discussing it in this article, refers to the total energy of a system. As objects move around over time, the energy associated with them—e.g., kinetic, gravitational potential, heat—might change forms, but if energy is conserved, then the total will remain the same.
- Conservation of energy applies only to isolated systems. A ball rolling across a rough floor will not obey the law of conservation of energy because it is not isolated from the floor. The floor is, in fact, doing work on the ball through friction. However, if we consider the ball and floor together, then conservation of energy will apply. We would normally call this combination the ball-floor system.
In mechanics problems, we are likely to encounter systems containing kinetic energy Ek gravitational potential energy (Ug), elastic—spring—potential energy (Us), and heat (thermal energy) (EH). Solving such problems often begins by establishing conservation of energy in a system between some initial time—subscript i—and at some later time—subscript f.
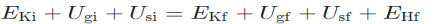
This could be expanded out as:
Collision of two bodies – direct central impact.
Impact occurs when two bodies collide with each other in a very short period of time, resulting relatively huge (impulsive) forces to be exerted between the bodies.
Example: striking of a hammer on a nail, a golf club on a ball
There are two types on impact:
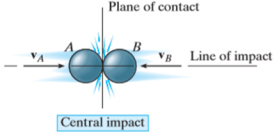
1) Central Impact
Central impact occurs when the direction of motion of the mass centers of the two colliding particles is along a line passing through the mass centers of the particles. This line is called the line of impact which is perpendicular to plane of contact.
2) Oblique impact
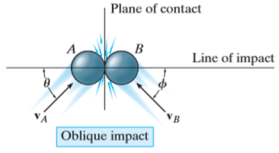
When the motion of one or both of the particles make an angle with the line of impact, then the impact is said to be oblique impact.
Impact occurs when two bodies collide with each other in a very short period of time, resulting relatively huge (impulsive) forces to be exerted between the bodies.
Example: striking of a hammer on a nail, a golf club on a ball
There are two types on impact:
- Central Impact
Central impact occurs when the direction of motion of the mass centers of the two colliding particles is along a line passing through the mass centers of the particles. This line is called the line of impact which is perpendicular to plane of contact.
2. Oblique impact
When the motion of one or both of the particles make an angle with the line of impact, then the impact is said to be oblique impact.
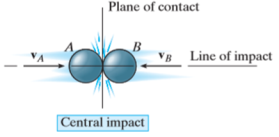
Consider two particles A and B involving the central impact of the shown in Fig. a
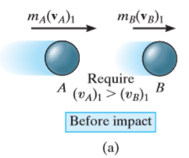
Let velocity of particle A is more than particle B.
During the collision the particles must be considered as deformable or nonrigid particles. The particles will undergo a period of deformation such that they exert an equal but opposite deformation impulse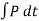 
on each other.
When the deformation becomes maximum, the relative motion of particle will become zero. Hence, the particle will move with same velocity v.
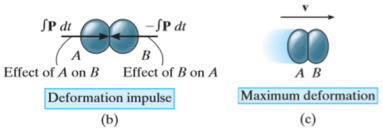
Then the particles will either return to their original shape or remain permanently deformed. This occurs after the period of restitution.
The equal but opposite restitution impulse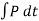 
pushes the particles apart from each another, shown in fig d. In reality, the physical properties of any two bodies are such that the deformation impulse will always be greater than that of restitution.
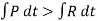
After the separation, the particles will have the final momenta as shown in Fig e.
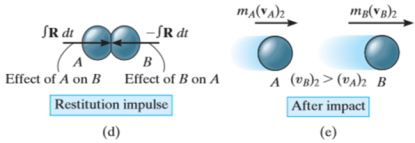
Momentum for the system of particles is conserved as during the collision the internal impulses of deformation and restitution cancel each other.
Hence,
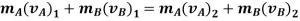
Applying impulse momentum equation for particle A during deformation phase (fig a, b and c), we get
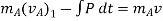
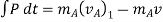
Now, applying impulse momentum equation for particle A during restitution phase (fig c, d and e), we get
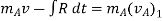
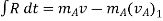
The ratio of the restitution impulse to the deformation impulse is called the coefficient of restitution.
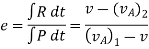
Similarly, Coefficient of restitution can be established for particle B.
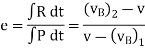
If velocity 
is unknown, then it can be eliminated from above equations and coefficient of restitution can be expressed in terms of the particle’s initial and final velocities
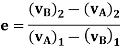
When, e = 1, the collision between the two particles is perfectly elastic. In perfectly elastic collision, the deformation impulse is equal and opposite to the restitution impulse. This is the ideal case and is impossible to achieve this case.
When e = 0, the collision between the two particles is perfectly plastic. In this case there is no restitution impulse so that after collision both particles couple or stick together and move with a common velocity.
