Unit - 1
Infinite series
Sequence –
A function f: N 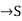 , where S is a non-empty set, is called sequence, for each nϵN.
, where S is a non-empty set, is called sequence, for each nϵN.
The sequence is written as f (1), f (2), f (3), f (4) ………. f(n).
Any sequence f(n) can be denoted as <f(n)> or {f(n)} or (f(n)).
Suppose f(n) = 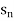
Then it can be written as - 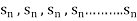 and can be denoted as <
and can be denoted as < >or {
>or {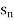 } or (
} or (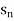 )
)
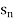 is the n’th term of the sequence.
is the n’th term of the sequence.
Example: suppose we have a sequence – 1, 4, 9, 16 ... and its n’th term is 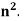
This sequence can be written as -<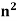 >
>
Example: 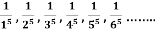 its n’th term will be
its n’th term will be 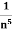 .and can be written as <
.and can be written as <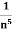 >
>
Types of sequences –
1. Finite sequence- A sequence which has finite number of terms is called finite sequence.
2. Infinite sequence- A sequence which is not finite, called infinite sequence.
Limit of a Sequence- A sequence <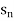 > is said to tend to limit “l”, when given any positive number ‘ϵ’, however small, we can always find an integer ‘m’ such that |
> is said to tend to limit “l”, when given any positive number ‘ϵ’, however small, we can always find an integer ‘m’ such that | 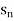 – l| <ϵ, for every for all, n≥m, and we can define this as follows,
– l| <ϵ, for every for all, n≥m, and we can define this as follows,
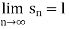
Example: If 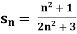 , then the limit of
, then the limit of 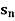 will be,
will be,
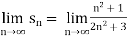 =
= 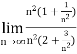 =
= 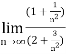 = ½
= ½
Hence the limit of the sequence is 1/2.
Some important limits to remember-
1.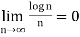
2. 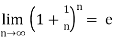
3. 
4. 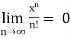
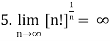
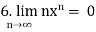
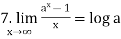


Convergent sequence- A sequence Sn is said to be convergent when it tends to a finite limit. That means the limit of a sequence Sn will be always finite in case of convergent sequence.
Divergent sequence- when a sequence tends to ±∞ then it is called divergent sequence.
Oscillatory sequence- when a sequence neither converges nor diverges then it is called oscillatory sequence.
Note- A sequence which neither converges nor diverges, is called oscillatory sequence.
A sequence converges to zero is called null.
Example-1: consider a sequence 2, 3/2, 4/3, 5/4, ……. here Sn = 1 + 1/n
Sol. As we can see that the sequence Sn is convergent and has limit 1.
According to def.

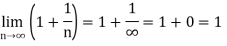
Example-2: consider a sequence Sn= n² + (-1) ⁿ.
Sol. Here we can see that; the sequence Sn is divergent as it has infinite limit.
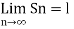
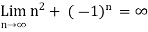
Example: suppose 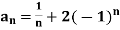 , here the sequence is said to be oscillate. Because it is between -2 and 2.
, here the sequence is said to be oscillate. Because it is between -2 and 2.
Series
Infinite series- If 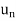 is a sequence, then
is a sequence, then 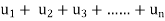 is called the infinite series.
is called the infinite series.
It is denoted by 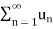 .
.
Examples of infinite series-
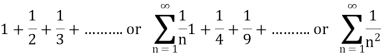
Convergent series - Suppose n→∞, Sn→ a finite limit ‘s’, then the series Sn is said to be convergent.
We can denote it as,
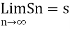
Divergent series- When Sn tends to infinity then the series is said to be divergent.
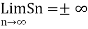
Oscillatory series- When Sn does not tend to a unique limit (finite or infinite), then it is called Oscillatory series.
Properties of infinite series –
1. The convergence and divergence of an infinite series is unchanged addition or deletion of a finite number of terms from it.
2. If positive terms of convergent series change their sign, then the series will be convergent.
3. Let 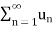 converges to s, let k be a non-zero fixed number then
converges to s, let k be a non-zero fixed number then 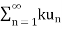 converges to ks.
converges to ks.
4. Let  converges to ‘l’ and
converges to ‘l’ and 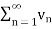 converges to ‘m’.
converges to ‘m’.
Example-1: check whether the series 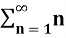 is convergent or divergent. Find its value in case of convergent.
is convergent or divergent. Find its value in case of convergent.
Sol. As we know that,
Sn = 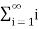
Therefore,
Sn = 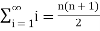
Now find out the limit of the sequence,
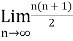 = ∞
= ∞
Here the value of the limit is infinity, so that the series is divergent as sequence diverges.
Example-2: check whether the series 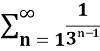 is convergent or divergent. Find its value in case of convergent.
is convergent or divergent. Find its value in case of convergent.
Sol. The general formula for this series is given by,
Sn = 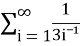 =
= 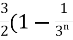 )
)
We get,
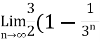 ) = 3/2
) = 3/2
Hence the series is convergent and its values is 3/2.
Example-3: check whether the series 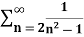 is convergent or divergent.
is convergent or divergent.
Sol. The general formula can be written as,
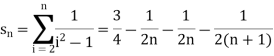
We get on applying limits,
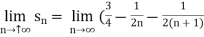 ) = 3/4
) = 3/4
This is the convergent series and its value is 3 / 4
Example-4: check whether the following series is convergent or divergent. If convergent, find its value.

Sol. n’th term of the series will be,
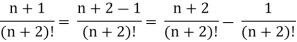
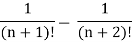
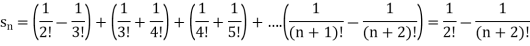
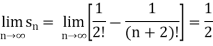
General properties of series
The general properties of series are-
1. The nature of a series does not change by multiplication of all terms by a constant k.
2. The nature of a series does not change by adding or deleting of a finite number of terms.
3. If two series 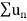 and
and 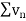 are convergent, then
are convergent, then 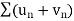 is also convergent.
is also convergent.
Exampple-1: Prove that the following series is convergent and find its sum.
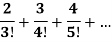
Sol. Here,
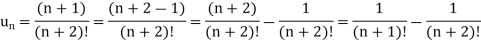
And
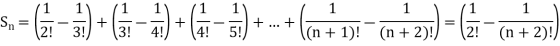
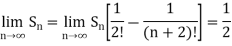
Hence the series is convergent and the limit is 1/2.
Example-2: Test the convergence of the series- 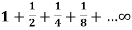
Sol. Here we can see that the given series is in geometric progression
As its first term is 1 and common ratio is ½.
Then we know that the sum of n terms of a geometric progression is-
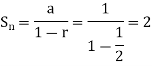
Hence the limit will be-
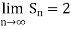
So that the series is convergent.
Key takeaways-

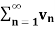
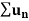
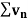
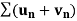
Positive term series-
If all the terms in an infinite series are positive after few negative terms, then the series said to be a positive term series.
Suppose,
-22-65+ 55 +69 99+125+………….is a positive term series.
If we remove these negative terms, then the nature of the series does not change.
Comparison test-
Statement-
Suppose we have two series of positive terms 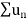 and
and 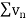 then,
then,
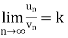 , where k is a finite number, then both series converges or diverges together.
, where k is a finite number, then both series converges or diverges together.
Proof- we know that by the definition of limits, there exist a positive number epsilon(ε)
Which is very small. Such that
According to definition (comparison test)
|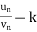 |<ε for n>m, that means
|<ε for n>m, that means
k-ε<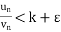 for n>m
for n>m
ignoring the first m terms of the series,
we get
k-ε< for n>m for all n ………………... (1)
for n>m for all n ………………... (1)
there will be two cases-
case-1: 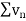 is convergent, then
is convergent, then
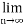 (
(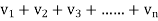 ) = r (say), where r is finite number
) = r (say), where r is finite number
From (1),

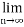 (
(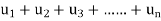 )<
)< (
(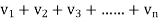 ) =
) = 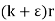
Therefore 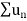 is also convergent.
is also convergent.
Case-2: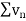 is divergent, then
is divergent, then
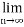 (
(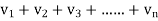 )→∞ …………………………... (2)
)→∞ …………………………... (2)
From eq. (1)
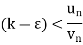
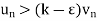
Then
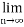 (
(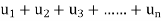 )<
)<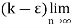 (
(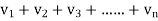 )
)
From (2)
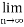 (
(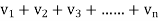 )→∞
)→∞
Hence, 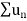 is also divergent.
is also divergent.
Example: Test the convergence of the following series.
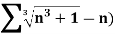
Sol. We have 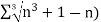
First, we will find 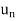 and the
and the 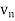

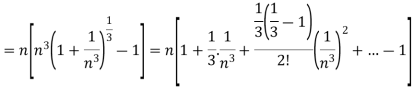
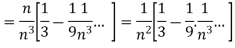
And
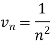
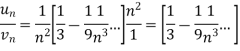


Here, we can see that, the limit is finite and not zero,
Therefore,  and
and 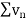 converges or diverges together.
converges or diverges together.
Since 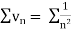 is of the form
is of the form 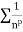 where p = 2>1
where p = 2>1
So that, we can say that,
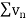 is convergent, so that
is convergent, so that 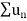 will also be convergent.
will also be convergent.
Example: Test the convergence of the following series-
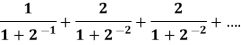
Sol. Here we have the series,
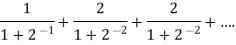
Now,
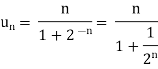

Now compare 
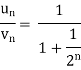
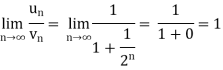
We can see that the limit is finite and not zero.
Here 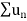 and
and 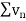 converges or diverges together since,
converges or diverges together since,
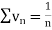 is the form of
is the form of 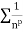 here p = 1,
here p = 1,
So that,
 is divergent then
is divergent then 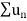 is also divergent
is also divergent
Example: Show that the following series is convergent.
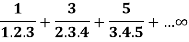
Sol.
Here we have
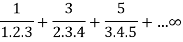
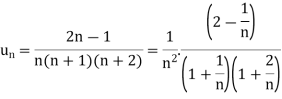
Suppose,
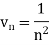
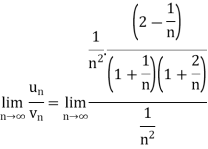
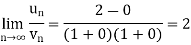
Which is finite and not zero.
By comparison test  and
and 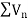 converge or diverge together.
converge or diverge together.
But, 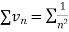
Is convergent. So that 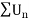 is also convergent.
is also convergent.
Example: Test the series:
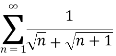
Sol. The series is,
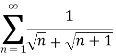
Now,

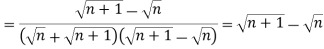
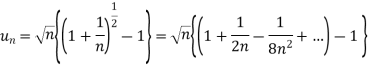
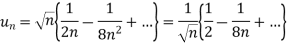
Take,


= 1/2
Which is finite and not zero.
Which is finite and not zero.
By comparison test  and
and 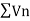 converge or diverge together.
converge or diverge together.
But,
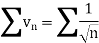
Is divergent. (p = ½)
So that  is divergent.
is divergent.
Ratio test
Statement- suppose 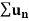 is a series of positive terms such that
is a series of positive terms such that 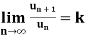 then,
then,
1. if k<1, the series will be convergent.
2. if k>1, then the series will be divergent.
Proof:
Case-1:
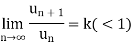
We know that from the definition of limits, it follows,
Therexists 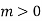 and
and 
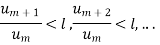
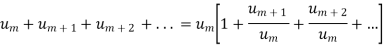

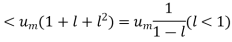
But,
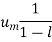
Is the finite quantity. So  is convergent.
is convergent.
Case-2:
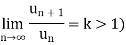
There could be some finite terms in starting which will never satisfy the condition,
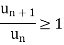
In this case we can find a number ‘m’,
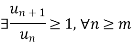
Ignoring the first ‘m’ terms, if we write the series as
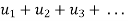
We have, in this case
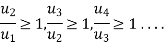
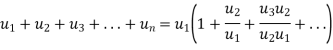
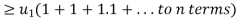
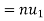
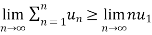 which
which 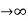
So that  is divergent.
is divergent.
Example: Test the convergence of the series whose n’th term is given below-
n’th term = 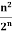
Sol. We have
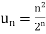 and
and 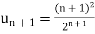
By D’Alembert ratio test,

So that by D’Alembert ratio test, the series will be convergent.
Example: Test for the convergence of the n’th term of the series given below-
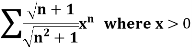
Sol. We have,

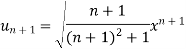
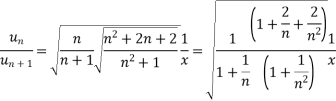

Now, by D’Alembert ratio test 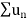 converges if
converges if 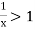 and diverges if
and diverges if 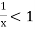
At x = 1, this test fails.
Now, when x = 1

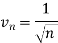
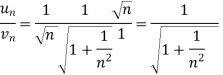
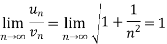
The limit is finite and not zero.
Then by comparison test, 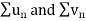 converges or diverges together.
converges or diverges together.
Since 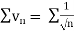 is the form of
is the form of 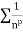 , in which
, in which 
Hence 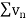 diverges then
diverges then 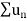 will also diverge.
will also diverge.
Therefore, in the given series  converges if x<1 and diverges if x≥1.
converges if x<1 and diverges if x≥1.
Key takeaways-
1. If 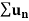 is a series of positive terms such that
is a series of positive terms such that 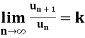 then,
then,
1. if k<1, the series will be convergent.
2. if k>1, then the series will be divergent.
3. Suppose we have two series of positive terms 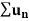 and
and  then,
then,
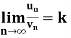 , where k is a finite number, then both series converges or diverges together.
, where k is a finite number, then both series converges or diverges together.
Statement- A series with positive terms f (1) + f (2) + f (3) + ……… f(n)+……...where, if we increase n, then f(n) decreases-
Converges or diverges according to the following integral-
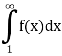
Is finite or infinite.
Proof: in the given figure, the area under the curve x=1 to x = n+1 lies between the sum of the areas of small rectangles and the sum of the areas of large rectangles.
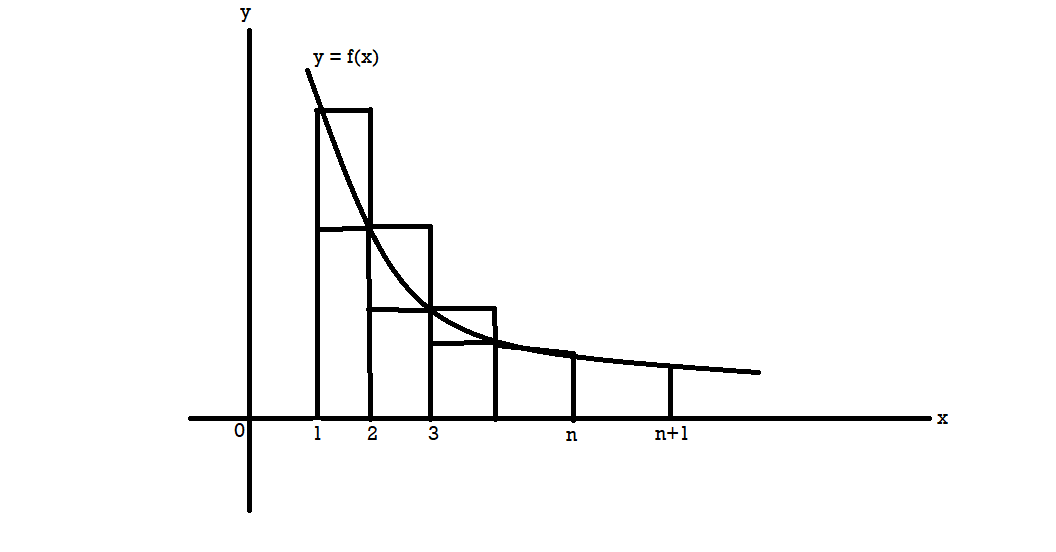
f (1), f (2), f (3) represents the height of the rectangles,
f (1) + f (2) + f (3) + ……… f(n) ≥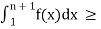 f (2) + f (3) + ……… f(n+1)
f (2) + f (3) + ……… f(n+1)

As n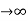 , from the second inequality that the integral has a finite value then
, from the second inequality that the integral has a finite value then 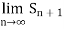 is also finite so that
is also finite so that 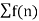 is convergent.
is convergent.
Same as the integral is infinite, then from the first inequality that 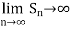 so that the series is divergent.
so that the series is divergent.
Example: Test the series for its convergence.

Sol. Let, f(x) = 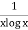
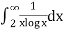 =
= 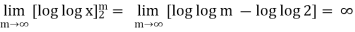
Here we notice that, by Cauchy’s integral test, the series is divergent.
Example: Test the series by integral test- 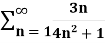
Sol. Here 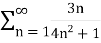 is positive and decreases when we increase n,
is positive and decreases when we increase n,
Now apply integral test,

Let,
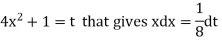
X = 1, t = 5 and x = ∞, t = ∞,
Now,
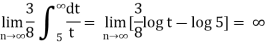
So, by integral test,
The series is divergent.
Example: Test the series by integral test-
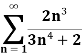
Sol. Here  decreases as n increases and it is positive.
decreases as n increases and it is positive.
By using integral test,
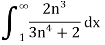
= 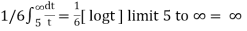
We get infinity,
So that the series is divergent.
Let  be a series of positive terms and
be a series of positive terms and
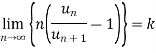
Then,
(1) if k >1,  is convergent and
is convergent and
(2) if k < 1, then  is divergent
is divergent
(3) this test fails if k = 1.
Proof: let us consider the series,
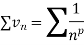
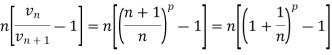
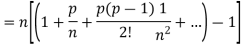
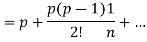
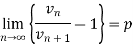
Case-1: in this case,
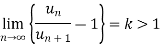
We choose a number ‘p’ for all k > p >1, comparing the series  with
with 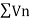 which is divergent,
which is divergent,
We get  will converge if after some fixed number of terms,
will converge if after some fixed number of terms,
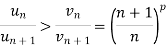
That means,
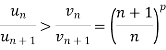
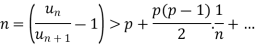
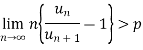
If k >p, which Is true. hence is convergent.
is convergent.
We can prove the second case similarly.
Example-1: Test the convergence of the following series.
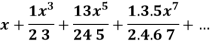
Sol. Neglecting the first term the series can be written as,
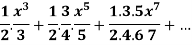
 are in A.P nth term
are in A.P nth term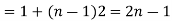
 are in A.P nth term
are in A.P nth term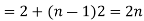
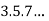 are in A.P nth term
are in A.P nth term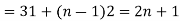
So that,
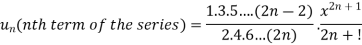
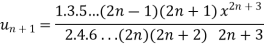
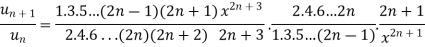
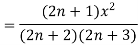
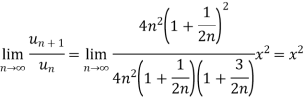
By ratio test  converges if |x|<1 and diverges if |x|>1, but if |x| = 1 the true. test fails,
converges if |x|<1 and diverges if |x|>1, but if |x| = 1 the true. test fails,
Then,
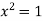 and
and
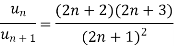
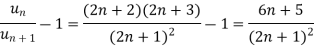
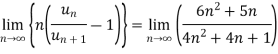
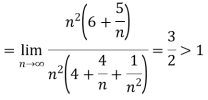
By Raabe’s test  converges hence the given series is convergent when |x|≤ 1 and divergent If |x| >1.
converges hence the given series is convergent when |x|≤ 1 and divergent If |x| >1.
Example-2: Test the convergence of the series,
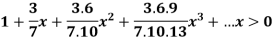
Sol. As we will neglect the first term, we get
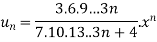
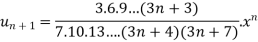
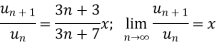
By ration test  is convergent when x<1 and divergent when x>1, when x= 1,
is convergent when x<1 and divergent when x>1, when x= 1,
The ratio test fails, then
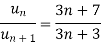
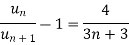
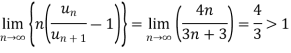
By Rabee’s test  is convergent, hence the given series is convergent when x≤ 1 and divergent If x >1.
is convergent, hence the given series is convergent when x≤ 1 and divergent If x >1.
Example-3: Test the nature of the following series:

Sol.
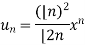
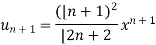
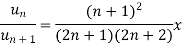
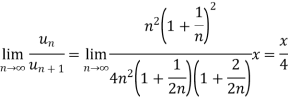
By ration test  is convergent when (x/4) <1 and divergent when x>4, when x= 4,
is convergent when (x/4) <1 and divergent when x>4, when x= 4,
The ratio test fails, then
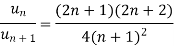
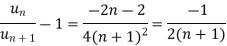
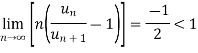
By Rabee’s test  is convergent, hence the given series is convergent when x<4 and divergent If x >=4.
is convergent, hence the given series is convergent when x<4 and divergent If x >=4.
Logarithmic test
Statement-
Suppose 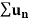 is series with positive terms such that
is series with positive terms such that
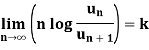
Then,
1. if k>1, then the series is convergent.
2. if k<1, then the series is divergent.
Proof: if k>1
Compare 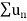 with
with 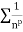 , if k>p>1 then
, if k>p>1 then 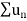 converges.
converges.
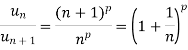
Taking log on both sides, we get
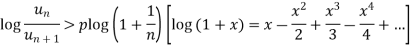
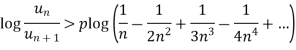
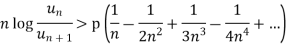
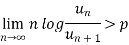
k>p which is true as k>p>1
Hence is convergent.
is convergent.
When p<1,
Similarly, when p<1, then 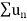 is divergent.
is divergent.
At p = 1, then this test fails.
Example: Test the convergence of the following series:
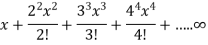
Sol. We have the series,
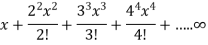
Here
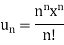
And
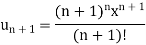
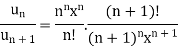
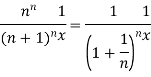
Which gives,
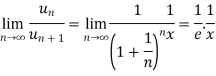
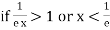 , the series is convergent.
, the series is convergent.
If  , the series is divergent.
, the series is divergent.
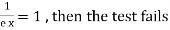 .
.
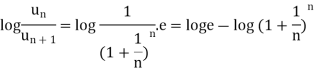
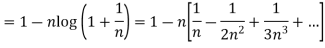
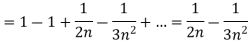
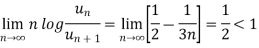
Thus, the series is divergent.
Key takeaways-

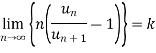
Then,
(1) if k >1,  is convergent and
is convergent and
(2) if k < 1, then  is divergent
is divergent
(3) this test fails if k = 1.
2. Suppose 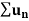 is series with positive terms such that
is series with positive terms such that

Then,
1. if k>1, then the series is convergent.
2. if k<1, then the series is divergent.
Let 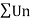 be a series of positive terms and let
be a series of positive terms and let
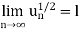
Then  is convergent when l<1 and diverges when l >1.
is convergent when l<1 and diverges when l >1.
Proof: case-1:
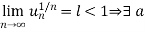 positive number
positive number 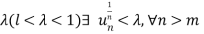
Or
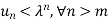
Since,
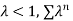
Is a geometric series with common ratio <1 so that the series will be convergent.
Case- 2:
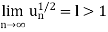
By the limit concept, we can find a number,
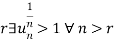
That means
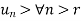
After 1st ‘r’ terms, each term is > 1

So that the series is divergent.
Example: Test the convergence of the series whose nth term is given below-
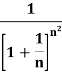
Sol.

By root test  is convergent.
is convergent.
Example: Test the convergence of the series whose nth term is given below-
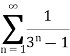
Sol.
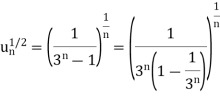

By root test  is convergent.
is convergent.
Example: show that the following series is convergent.
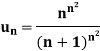
Sol.
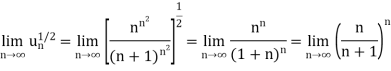
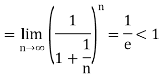
By root test  is convergent.
is convergent.
Example: Test the convergence of the following series:

Sol. Here, we have,
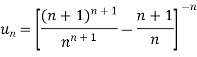


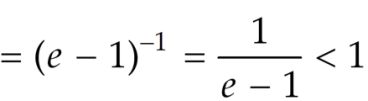
Therefore, the given series is convergent.
Key takeaways-
If 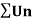 be a series of positive terms and let
be a series of positive terms and let
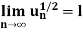
Then  is convergent when l<1 and diverges when l >1.
is convergent when l<1 and diverges when l >1.
First, we will understand about alternating series,
When the terms in a series are alternately negative, then the series is known as alternating series.
For example:

Leibnitz test for the convergence of an alternating series:
The given series will be convergent if it follows the rules given below-
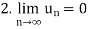
Example: Test the convergence of the following alternating series:
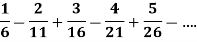
Sol. Here in the series, we have
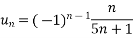
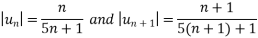
First condition-
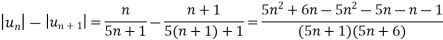
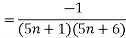
So that,
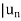 | > |
| > |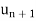 |
|
That means, each term is not numerically less than its preceding terms.
Now second condition-
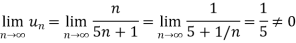
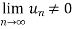
Both conditions are not satisfied for convergence.
Hence the given series is not convergent. It is oscillatory.
Example: Test the following series for the convergence-
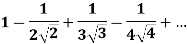
Sol. We have the given series, now
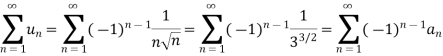
We see that, this is an alternating series,
Here,



Also,

By Leibnitz’s test the series is convergent.
Key takeaways-
ii. 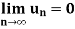
Absolute convergence
A series  is said to be absolutely convergent if the series
is said to be absolutely convergent if the series 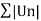 is convergent.
is convergent.
For example- suppose the following series,

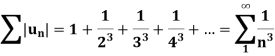
By p- series test, we can say that 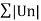 is convergent.
is convergent.
Hence  is absolutely convergent.
is absolutely convergent.
Note-
2. An absolute convergent series will be convergent but the converse may not be true.
Example: Test for absolute convergence:
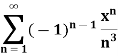
Sol. Let the series is 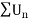 ,
,
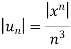
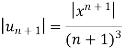
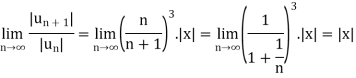
By ratio test,
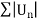 is convergent, if |x|<1.
is convergent, if |x|<1.
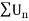 is absolutely convergent if |x|< 1.
is absolutely convergent if |x|< 1.
Example: Show that the series 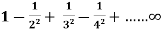 is absolutely convergent.
is absolutely convergent.
Sol. We have,
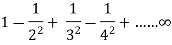
|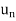 | =
| =  and |
and |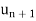 | =
| = 
The first condition and second conditions are-
1. |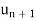 |<|
|<|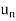 |
|
2. 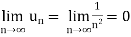
Both the conditions are satisfied.
So that we can say that by Leibnitz’s rule, the series is convergent.
The series is also convergent by p-test as p = 2 > 1.
Hence the given series is absolutely convergent.
Example: Test the convergence/Divergence of the series:
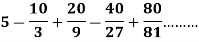
Sol. Here the given series is alternately negative and positive, which is also a geometric infinite series.
1. suppose,
S = 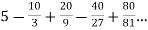
According to the conditions of geometric series,
Here, a = 5, and common ratio (r) = -2/3
Thus, we know that,
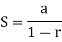
So,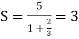
Sum of the series is finite, which is 3.
So, we can say that the given series is convergent.
Now.
Again, sum of the positive terms,

The series is geometric, then
A = 5 and r = 2/3, then
Sum of the series,
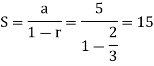
Sum of the series is finite then the series is convergent.
Both conditions are satisfied, then the given series is absolutely convergent.
Conditional convergence-:
If the series 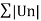 is divergent and
is divergent and  is convergent then
is convergent then  is said to be conditionally convergent
is said to be conditionally convergent
Example: Show that the series 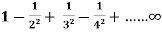 is absolutely convergent.
is absolutely convergent.
Sol. We have,
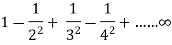
 | =
| = 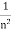 and |
and |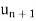 | =
| = 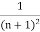
The first condition and second conditions are-
1. |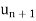 |< |
|< |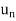 |
|
2. 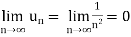
Both the conditions are satisfied.
So that we can say that by Leibnitz’s rule, the series is convergent.
The series is also convergent by p-test as p = 2 > 1.
Hence the given series is absolutely convergent.
Example: Test the convergence/Divergence of the series:
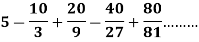
Sol. Here the given series is alternately negative and positive, which is also a geometric infinite series.
1. suppose,
S = 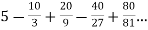
According to the conditions of geometric series,
Here, a = 5, and common ratio (r) = -2/3
Thus, we know that,
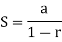
So,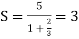
Sum of the series is finite, which is 3.
So, we can say that the given series is convergent.
Now.
Again, sum of the positive terms,
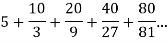
The series is geometric, then
A = 5 and r = 2/3, then
Sum of the series,
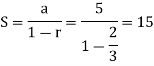
Sum of the series is finite then the series is convergent.
Both conditions are satisfied, then the given series is absolutely convergent.
Example: Test the series for absolute/conditional convergence.
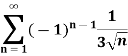
Sol. The given series is an alternating series of the form,
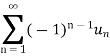
Here,
1. 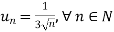
2. 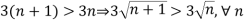
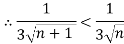
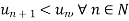
And,
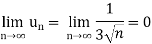
Hence bt Leibnitz’s test, the given series is convergent,
But,

Is divergent by p-series test.
So that, the given series is conditionally convergent.
Example: Test for the convergence of the series:
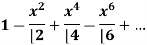
Sol. The given series is,
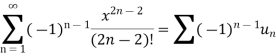

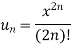
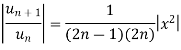
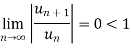
By ratio test series 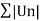 converges, so that the series is convergent.
converges, so that the series is convergent.
Example: Test for absolute convergence:
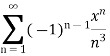
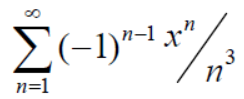
Sol. Let the series is  ,
,
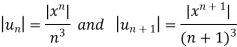
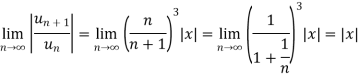
By ratio test,
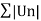 is convergent, if |x|<1.
is convergent, if |x|<1.
 is absolutely convergent if |x|< 1.
is absolutely convergent if |x|< 1.
Key takeaways-

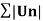
Taylor’s Theorem-
If f (x + h) is a function of h which can be expanded in the ascending powers of h and is differentiable by any number of times with respect to h, then-
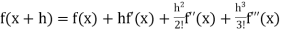 + …….+
+ …….+ 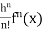 + ……..
+ ……..
Which is called Taylor’s theorem.
If we put x = a, we get-
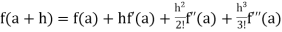 + …….+
+ …….+ 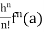 + …….. (1)
+ …….. (1)
Maclaurin’s Theorem-
If we put a = 0 and h = x then equation (1) becomes-
 + …….
+ …….
Which is called Maclaurin’s theorem.
Note – if we put h = x - a then there will be the expansion of F(x) in powers of (x – a)
We get-
 + …….
+ …….
Example: Express the polynomial 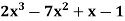 in powers of (x-2).
in powers of (x-2).
Sol. Here we have,
f(x) = 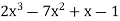
differentiating the function w.r.t. x-
f’(x) = 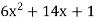
f’’(x) = 12x + 14
f’’’(x) = 12
f’’’’(x)=0
now using Taylor’s theorem-
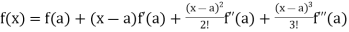 + ……. (1)
+ ……. (1)
Here we have, a = 2,
Put x = 2 in the derivatives of f(x), we get-
f (2) = 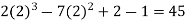
f’ (2) = 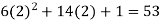
f’’ (2) = 12(2) +14 = 38
f’’’(2) = 12 and f’’’’(2) = 0
now put a = 2 and substitute the above values in equation (1), we get-
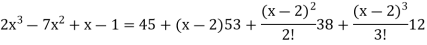
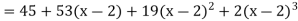
Example: Expand sin x in powers of 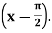
Sol. Let f(x) = sin x
Then,
= 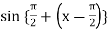
By using Taylor’s theorem-
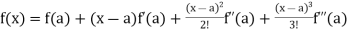 + ……. (1)
+ ……. (1)
Here f(x) = sin x and a = π/2
f’(x) = cosx, f’’(x) = - sin x, f’’’(x) = - cos x and so on.
Putting x = π/2, we get
f(x) = sin x = 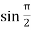 = 1
= 1
f’(x) = cos x = 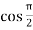 = 0
= 0
f’’(x) = -sin x = 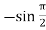 = -1
= -1
f’’’(x) = -cos x = 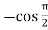 = 0
= 0
from equation (1) put a =  and substitute these values, we get-
and substitute these values, we get-
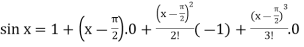 + …….
+ …….
= 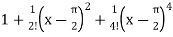 ………………………..
………………………..
Example: Find the Taylor’s series for the function f(x) = 3x² - 6x + 5 in ascending powers of x-3.
Sol. We know that the Taylor’s theorem for the function f(x) in ascending powers of (x – a) is,
f(x) = f(a) + (x – a) f’(a) + 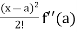 + ………
+ ……… . …………. (1)
. …………. (1)
here,
f(x) = 3x² - 6x + 5 and a = 3. So that f(a) = 14
Now, we will find out the derivatives,
f’(x) = 6x – 6 and f’ (3) = 12
f’’(x) = 6 and f’’ (3) = 6
f’’’(x) = 0 and f’’’(x) = 14
put these values in Taylor’s theorem, we get
3x² - 6x + 5 = 14 + 12(x-3) + 6 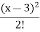 +…………. Ans.
+…………. Ans.
Example: Expand the function 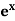 in ascending powers of (x – 1) by using Taylor’s theorem.
in ascending powers of (x – 1) by using Taylor’s theorem.
Sol. We know that the Taylor’s theorem for the function f(x) in ascending powers of (x – a) is,
f(x) = f(a) + (x – a) f’(a) + 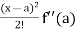 + ………
+ ………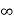 . …………. (1)
. …………. (1)
here f(x) = 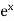 and a = 1
and a = 1
now,
f’(x) = 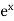 and f’(a) = e
and f’(a) = e
f’’(x) =  and f’’(a) = e
and f’’(a) = e
put these values in equation (1),
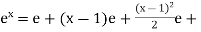 …………….
…………….
Take ‘e’ as common,
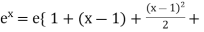 …………….}
…………….}
Which is the required expansion.
Example: Expand 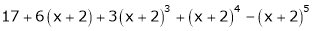 in powers of x using Taylor’s theorem,
in powers of x using Taylor’s theorem,
Solution:
Here
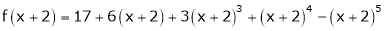
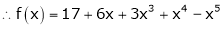
i.e., 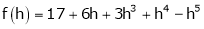
Here
h = 2
 By Taylors series
By Taylors series
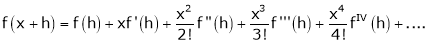 … (1)
… (1)
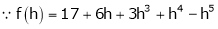
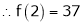
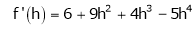

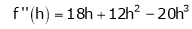
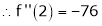
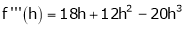
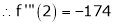
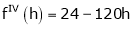
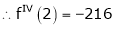
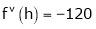
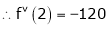
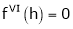
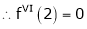
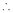 By equation (1)
By equation (1)
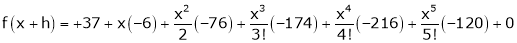
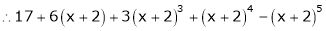

Example: By using Maclaurin’s series expand tan x.
Sol.
Let-


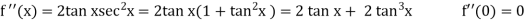
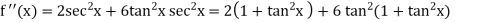

Put these values in Maclaurin’s series we get-
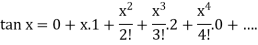
Example: Expand 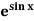 by using Maclaurin’s series.
by using Maclaurin’s series.
Sol.
Let

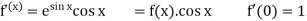


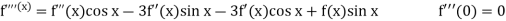
Put these values in Maclaurin’s series-
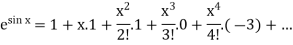
Or
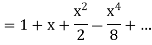
Key takeaways-
 + …….+
+ …….+ 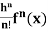 + ……..
+ ……..
2. Maclaurin’s Theorem-
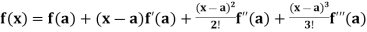 + …….
+ …….
Definition-
“An asymptote of a curve is straight line at a finite distance from the origin, to which a tangent to the curve tends as the point of contact recedes to infinity.”
Or in other words-
A straight line is said to be an asymptote to a curve, if as a point P moves to infinity along the curve, the perpendicular distance of P from the straight line tends to zero.
Vertical asymptote-
A line x = a is called a vertical asymptote to the curve of the function f if  or
or 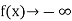 as x approaches a from either side. In vertical asymptotes, we have used limits to describe the behavior of f (x) as x approaches a.
as x approaches a from either side. In vertical asymptotes, we have used limits to describe the behavior of f (x) as x approaches a.
Horizontal asymptote-
A line y = L is said to be a horizontal asymptote to the curve of the function f if i.e., 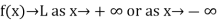
Note-
Example: Find the asymptotes of the following curve-

Sol.
Here the highest power of x is 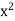 and the coefficient is
and the coefficient is 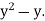
We can find the asymptote parallel to x-axis as-
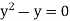
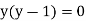
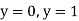
And the highest power of y is 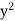 and its coefficient is
and its coefficient is 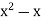 .
.
The asymptotes parallel to y-axis, are given by-
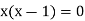
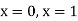
Therefore, the asymptotes are x = 0, x = 1, y = 0 and y = 1.
Example: Find the vertical asymptote of 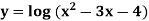 .
.
Sol.
 has vertical asymptotes when
has vertical asymptotes when  ,
,
thus x = 4 and x = -1 are the vertical asymptotes of
Asymptotes of polar curves-
It can be shown that
Example: Find the horizontal asymptote of the function given below-
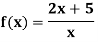
Sol.
In order to find the horizontal asymptotes, we find-
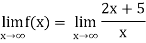
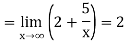
Hence the horizontal asymptote is the line y = 2.
Example: Find the asymptotes parallel to x-axis and y-axis of the following curve-
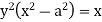
Sol.
We can write the given equation as-
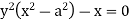
Asymptote parallel to x-axis-
Now by putting the coefficient of 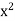 equals to zero, we get
equals to zero, we get
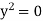
Which gives- 
Asymptote parallel to y-axis-
By putting the coefficient of 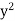 equals to zero, we get
equals to zero, we get
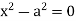
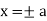
Hence 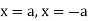 are the asymptotes parallel to y-axis.
are the asymptotes parallel to y-axis.
Slant asymptote-
Definition:
A line y = mx + c (m is non-zero) is an oblique asymptote or slant asymptote to the graph of the function f if
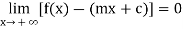
Or
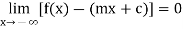
Example: Find the slant asymptote of
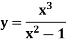
Sol.
Here we will find m and c,
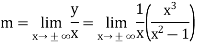
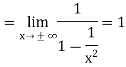
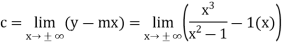
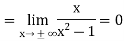
Hence the slant asymptote is y = x
Key takeaways-
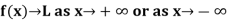
References: