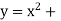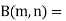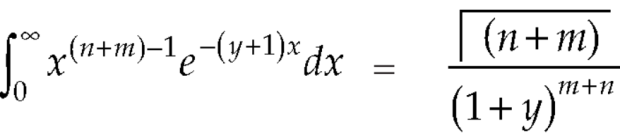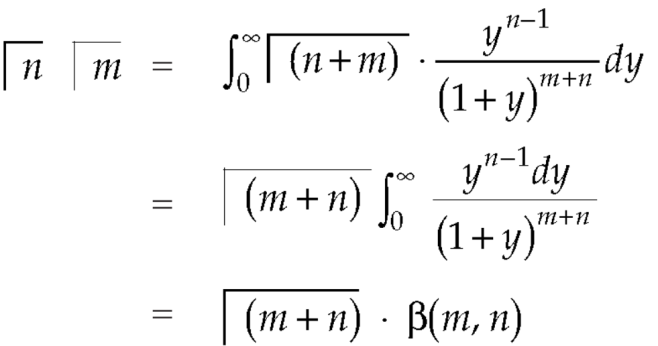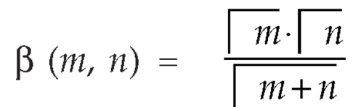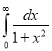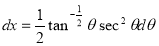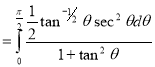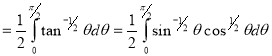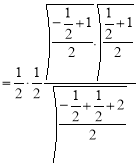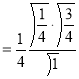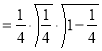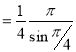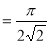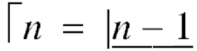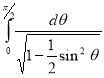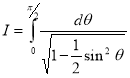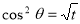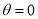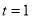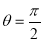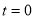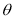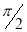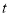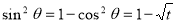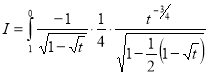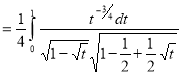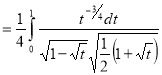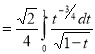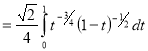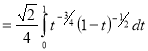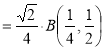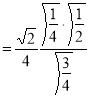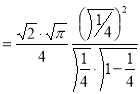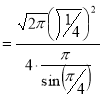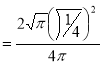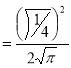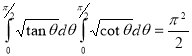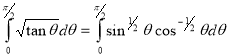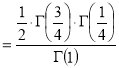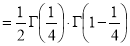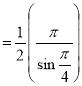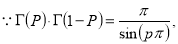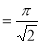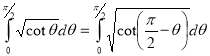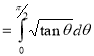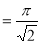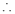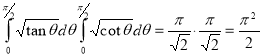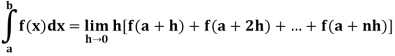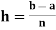Unit - 3
Applications of single and Multiple integration
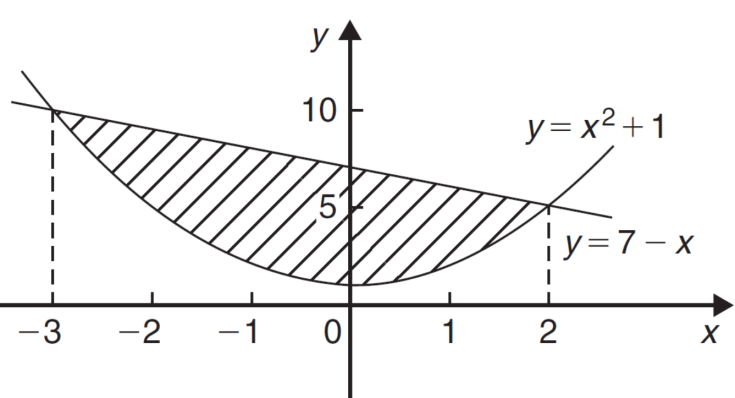
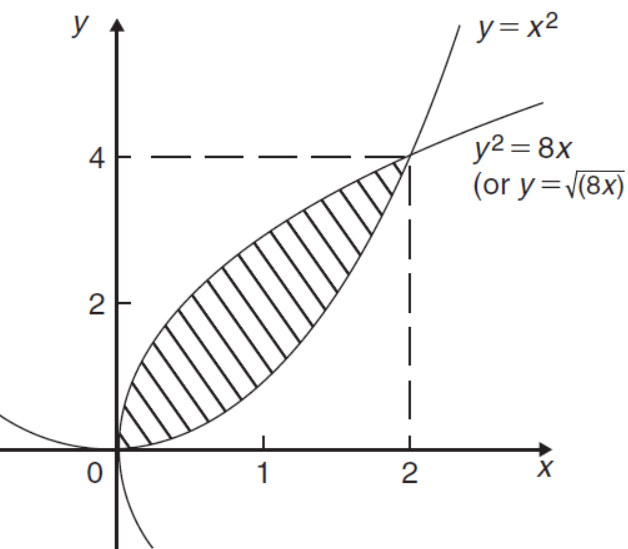
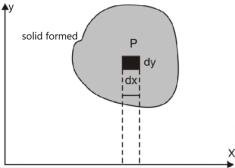
Area under and between the curves-
Total shaded area will be as follows of the given figure (by using definite integrals)-
Total shaded area = 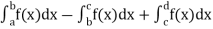
Example-1: Determine the area enclosed by the curves-
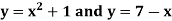
Sol. We know that the curves are equal at the points of interaction, thus equating the values of y of each curve-
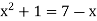
Which gives-
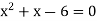
By factorization,
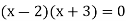
Which means,
x = 2 and x = -3
By determining the intersection points the range the values of x have been found-
x | -3 | -2 | -1 | 0 | 1 | 2 |
| 10 | 5 | 2 | 1 | 2 | 5 |
And
x | -3 | 0 | 2 |
y = 7 - x | 10 | 7 | 5 |
We get the following figure by using above two tables-
Area of shaded region = 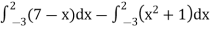
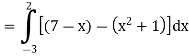
= 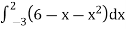
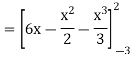
= (12 – 2 – 8/3) – (-18 – 9/2 + 9)
= 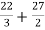
= 125/6 square unit
Example-2: Determine the area bounded by three straight lines y = 4 – x, y = 3x and 3y = x
Sol. We get the following figure by using the equations of three straight lines-
y = 4 – x, y = 3x and 3y = x
Area of shaded region-
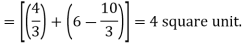
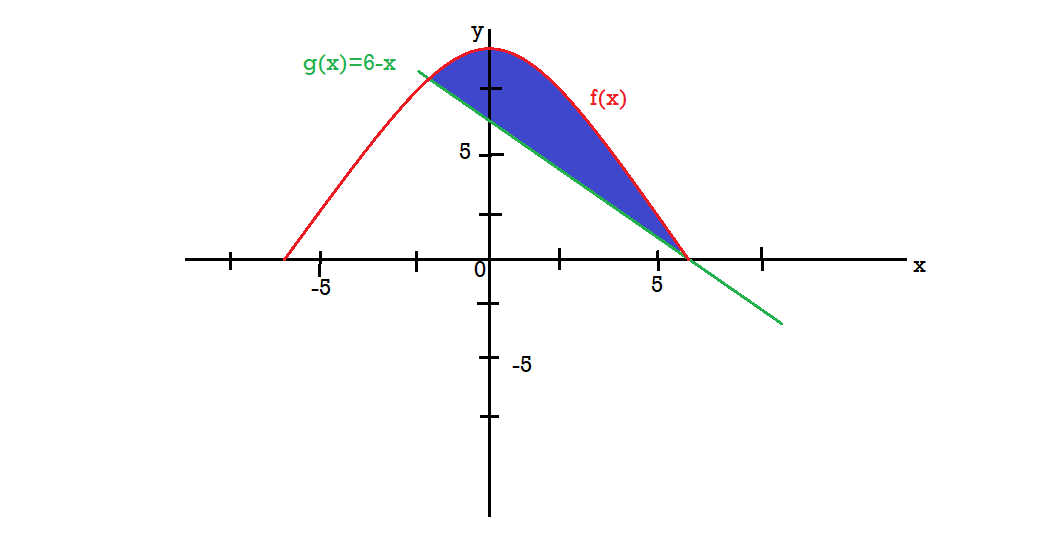
Example-3: Find the area enclosed by the two functions-
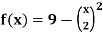 and g(x) = 6 – x
and g(x) = 6 – x
Sol. We get the following figure by using these two equations
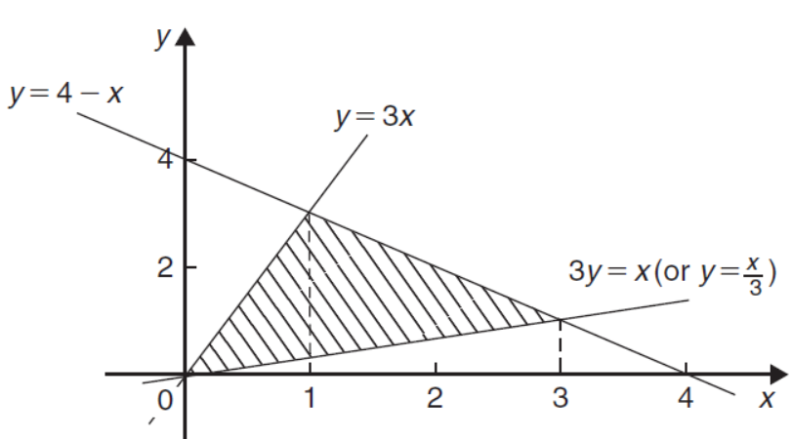
To find the intersection points of two functions f(x) and g(x)-
f(x) = g(x)
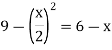
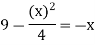
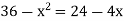
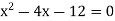
On factorizing, we get-
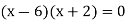
x = 6, -2
Now
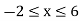
Then, area under the curve-
A = 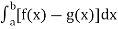
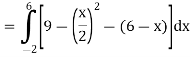
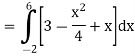
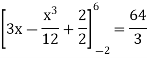
Therefore, the area under the curve is 64/3 square unit.
Areas and volumes of revolutions-
The volume of revolution (V) is obtained by rotating area A through one revolution about the x-axis is given by-
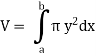
Suppose the curve x = f(y) is rotated  about y-axis between the limits y = c and y = d, then the volume generated V, is given by-
about y-axis between the limits y = c and y = d, then the volume generated V, is given by-
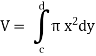
Example-1: Find the area enclosed by the curves 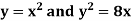 and if the area is rotated
and if the area is rotated  about the x-axis, then determine the volume of the solid of revolution.
about the x-axis, then determine the volume of the solid of revolution.
Sol. We know that, at the point of intersection the coordinates of the curve are equal. So that first we will find the point of intersection-
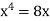
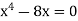
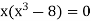
We get,
x = 0 and x = 2
The curve of the given equations will look like as follows-
Then,
The area of the shaded region will be-
A = 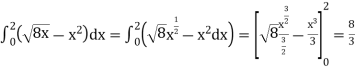
So that the area will be 8/3 square unit.
The volume will be
= (volume produced by revolving 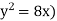 – (volume produced by revolving
– (volume produced by revolving 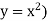
= 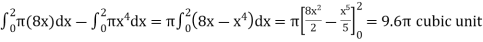
Method of cylindrical shells-
Let f(x) be a continuous and positive function. Define R as the region bounded above by the graph f(x), below by the x-axis, on the left by the line x = a and on the right x = b, then the volume of the solid of revolution formed by revolving R around the y-axis is given by
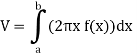
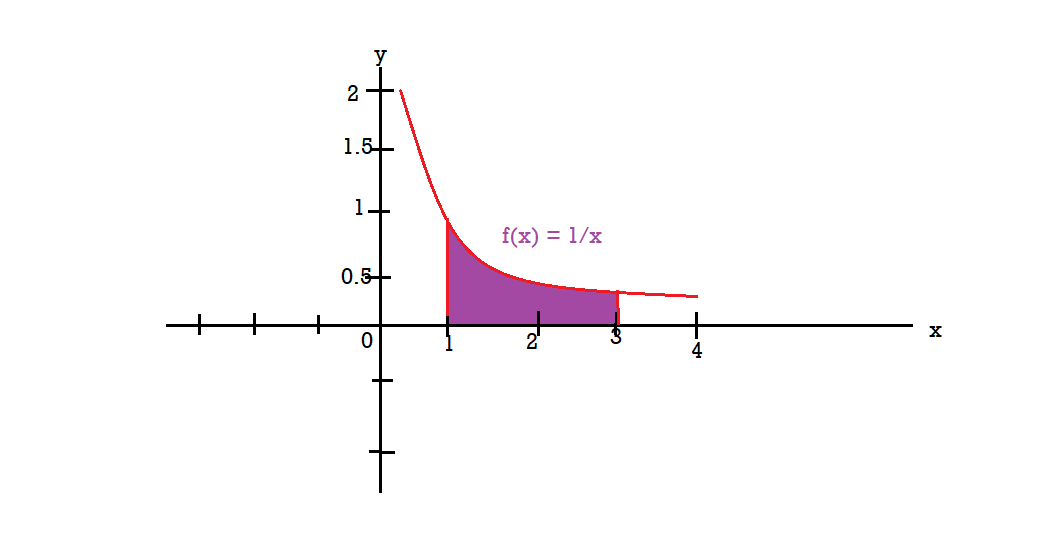
Example-2: Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 1/x over the interval [1, 3].
Sol. The graph of the function f(x) = 1/x will look like-
The volume of the solid of revolution generated by revolving R (violet region) about the y-axis over the interval [1, 3]
Then the volume of the solid will be-
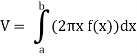
Example-3: Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 2x - x² over the interval [0, 2].
Sol. The graph of the function f(x) = 2x - x² will be-
The volume of the solid is given by-
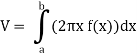
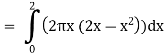
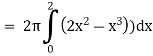
= 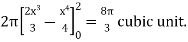
Key takeaways-
The volume of revolution (V) is obtained by rotating area A through one revolution about the x-axis is given by-
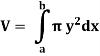
2. Method of cylindrical shells-
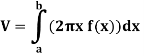
Double integral –
Before studying about multiple integrals, first let’s go through the definition of definition of definite integrals for function of single variable.
As we know, the integral
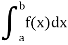
Where is belongs to the limit a ≤ x ≤ b
This integral can be written as follows-
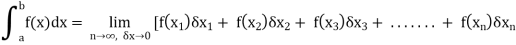
Now suppose we have a function f (x, y) of two variables x and y in two-dimensional finite region Rin xy-plane.
Then the double integration over region R can be evaluated by two successive integrations
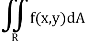
Evaluation of double integrals-
If A is described as 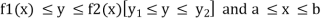
Then,
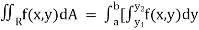 ] dx
] dx
Let do some examples to understand more about double integration-
Example-: Evaluate 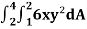 , where dA is the small area in xy-plane.
, where dA is the small area in xy-plane.
Sol. Let, I = 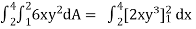
= 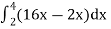
= 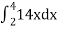
= 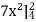
= 84 sq. unit.
Which is the required area,
Example-2: Evaluate 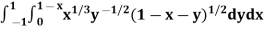
Sol. Let us suppose the integral is I,
I = 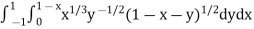
Put c = 1 – x in I, we get
I = 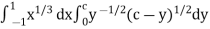
Suppose, y = ct
Then dy = c
now we get,
I = 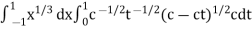
I = 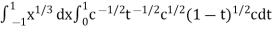
I = 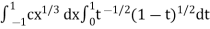
I = 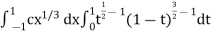
I =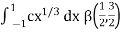
As we know that by beta function,
Which gives,
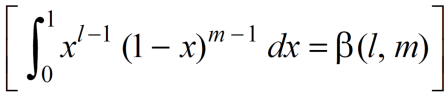
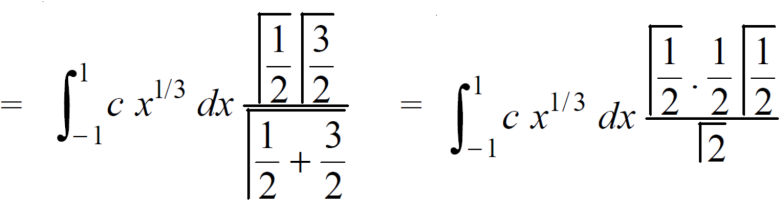
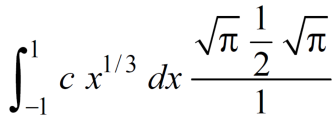
Now put the value of c, we get
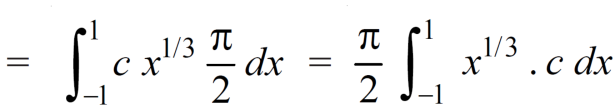
Example-3: Evaluate the following double integral,
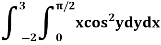
Sol. Let,
I = 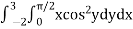
On solving the integral, we get
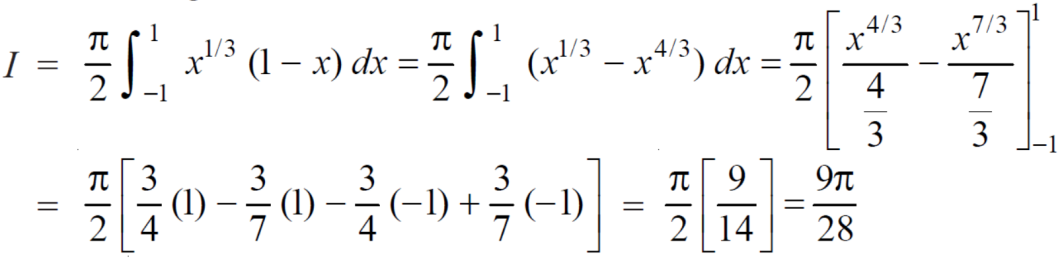
Change of order of integration
The limits of integration change when we change the order of integration.
We draw the rough diagram of the region of integration to find the new limits.
Example-1: Change the order of integration in the double integral-
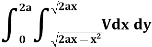
Sol.
Limits are given-
x = 0, x = 2a
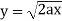
And
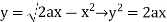
and
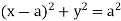
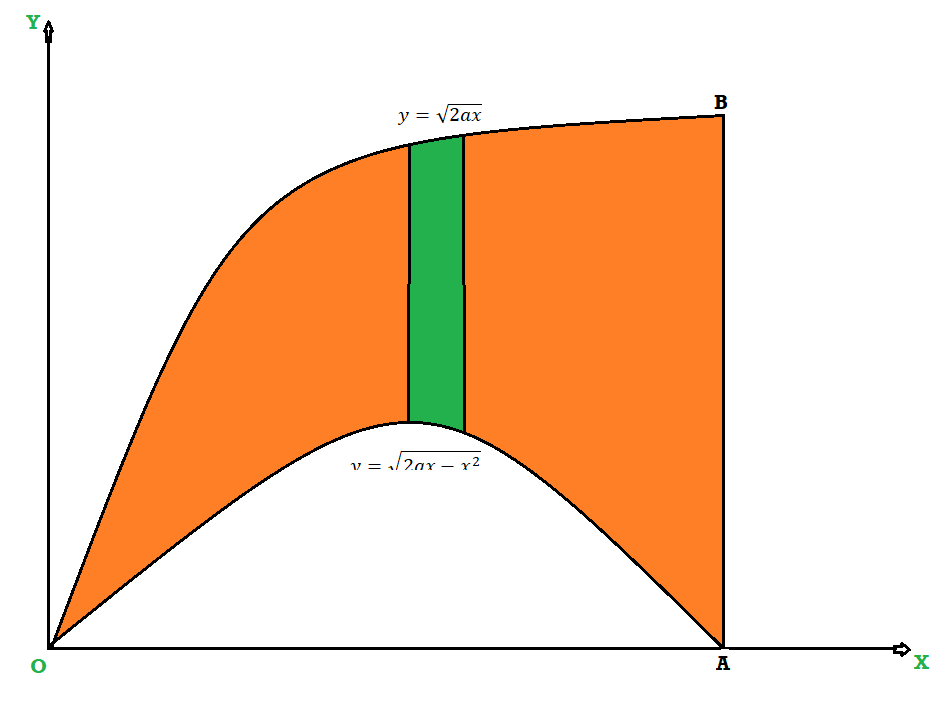
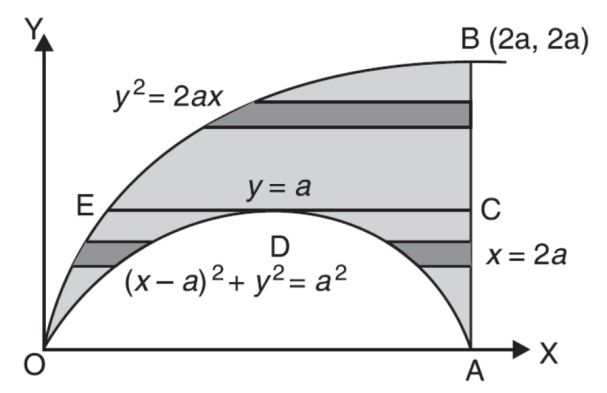
The area of integration is the shaded portion of OAB. On changing the order of integration first we will integrate with respect to x, the area of integration has three portions BCE, ODE and ACD,
Now-
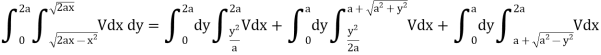
Which is the required answer.
Example-2: Change the order of integration for the integral 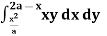 and evaluate the same with reversed order of integration.
and evaluate the same with reversed order of integration.
Sol:
Given, I = 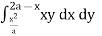 … (1)
… (1)
In the given integration, limits are
y= 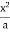 , y = 2a – x and x = 0, x = a
, y = 2a – x and x = 0, x = a
The region bounded by x2 = ay, x + y = 2a
And x = 0, x = a is as shown in Fig.
Here we have to change order of Integration. Given the strip is vertical.
Now take horizontal strip SR.
To take total region, divide region into two parts by taking line y = a.
1 st Region:
Along strip, y constant and x varies from x = 0 to x = 2a – y. Slide strip IIelto x-axis therefore y varies from y = a to y = 2a.
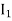 = dyxy dx ......… (2)
= dyxy dx ......… (2)
2nd Region:
Along strip, y constant and x varies from x = 0 to x= . Slide strip IIel to x-axis therefore x-varies from y = 0 to y = a.
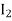 = dyxy dx … (3)
= dyxy dx … (3)
From Equation (1), (2) and (3),
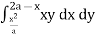 = dyxy dx + dyxy dx
= dyxy dx + dyxy dx
= 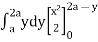 + y dy
+ y dy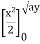
=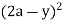 dy + (ay) dy = y (4a2 – 4ay + y2) dy + ay2dy
dy + (ay) dy = y (4a2 – 4ay + y2) dy + ay2dy
= (4a2 y – 4ay2 + y3) dy + y2dy
= 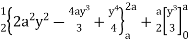
= 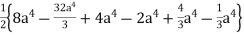 +
+ 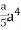
= a4
Example-3: Evaluate
I = 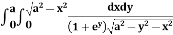
Soln.:
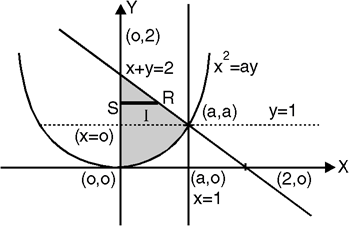
Given: I = 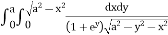 … (1)
… (1)
In the given integration, limits are
x = 0, x = a, y = 0, y = 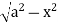
The bounded region is as shown in Fig. **.
In the given, strip is vertical. Now take horizontal strip SR. along strip y constant and x varies from x = 0 to
x = 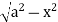 . Slide strip IIel to X-axis therefore y varies from y = 0 to y = a.
. Slide strip IIel to X-axis therefore y varies from y = 0 to y = a.
I = dy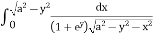
= 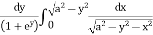
Put a2 – y2 = b2
I = 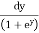
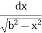
= 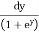 =
= 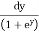
= 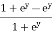 dy =
dy = 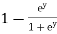 dy
dy
= 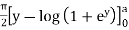
=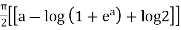
= 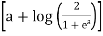
= 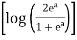 [∵ a = a loge]
[∵ a = a loge]
I = dy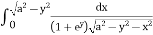 =
= 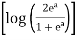
Example-4: Express as single integral and evaluate dy dx + dy dx.
Soln.:
Give: I = dy dx + dy dx
I = I1 + I2
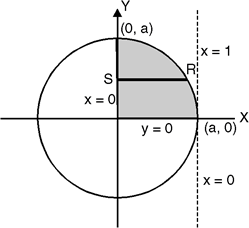
The limits of region of integration I1 are
x = – ; x = and y = 0, y = 1 and I2 are x = – 1,
x = 1 and y = 1, y = 3.
The region of integration is as shown in Fig.
To consider the complete region take a vertical strip SR along the strip y varies from y = x2 to
y = 3 and x varies from x = –1 to x = 1. Fig. 6.7
I = 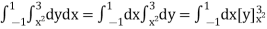
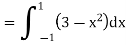
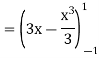
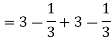
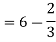
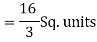
Double integration in polar coordination -
In polar coordinates, we need to evaluate
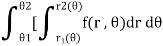
Over the region bounded by θ1 and θ2.
And the curves r1(θ) and r2(θ)
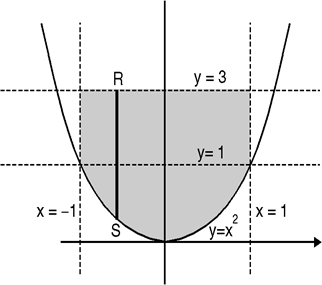
Example-1: Evaluate the following by changing to polar coordinates,
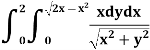
Sol. In this problem, the limits for y are 0 to 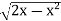 and the limits for are 0 to 2.
and the limits for are 0 to 2.
Suppose,
y = 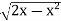
squaring both sides,
y² = 2x - x²
x² + y² = 2x
but in polar coordinates,
we have,
r² = 2r cosθ
r = 2 cosθ
from the region of integration, r lies from 0 to 2 cosθ and θ varies from 0 to π / 2.
As we know in case of polar coordinates,
Replace x by r cosθ and y by r sinθ, dy dx by r drdθ,
We get,
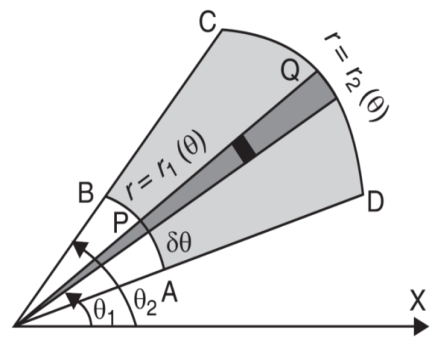
Example-2: Evaluate the following integral by converting into polar coordinates.
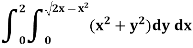
Sol. Here limits of y,
y = 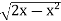
y² = 2x - x²
x² + y² = 2x
x² + y² - 2x = 0 ……………… (1)
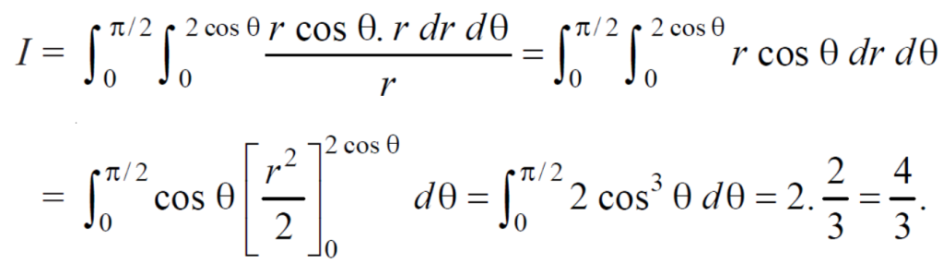
Eq. (1) represent a circle whose radius is 1 and centre is (1, 0)
Lower limit of y is zero.
Region of integration in upper half circle,
First, we will convert into polar coordinates,
By putting
x by r cos θ and y by r sinθ, dy dx by r drdθ,
limits of r are 0 to 2 cosθ and limits of θ are from 0 to π / 2.
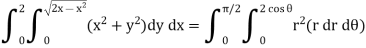
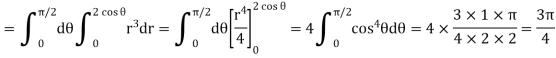
Example-3: Evaluate 
Sol. Let the integral,
I = 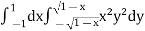
=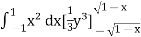
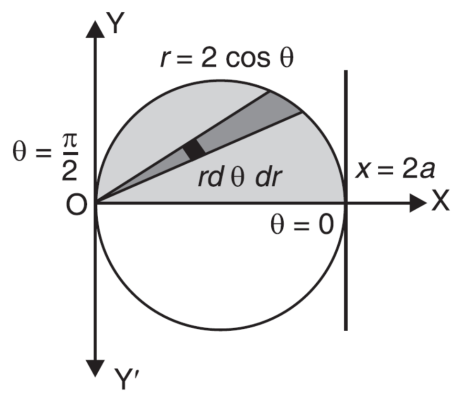
Put x = sinθ
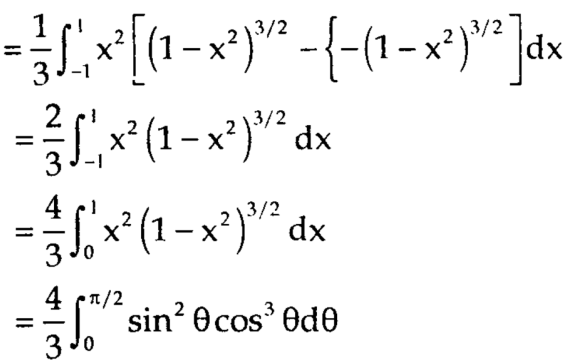
= π / 24 ans.
Area of double integration
Area in Cartesian coordinates-
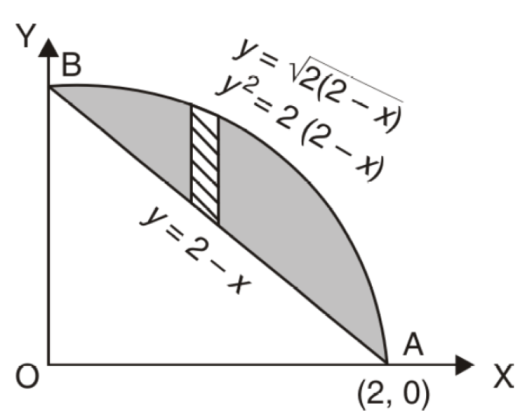
Example-1: Find the area enclosed by two curves using double integration.
y = 2 – x and y² = 2 (2 – x)
Sol. Let,
y = 2 – x ………………... (1)
and
y² = 2 (2 – x) ………………... (2)
on solving eq. (1) and (2)
we get the intersection points (2,0) and (0,2),
we know that,
Area = 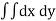
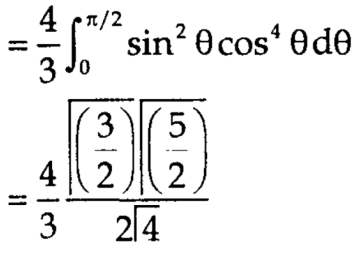
Here we will find the area as below,
Area = 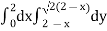
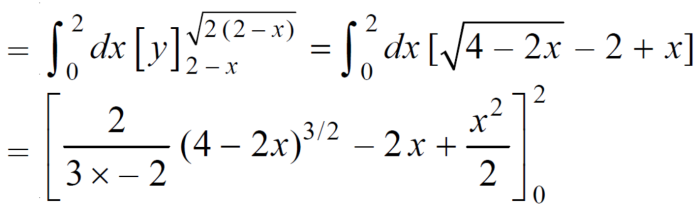
Which gives,
= (- 4 + 4 /2) + 8 / 3 = 2 / 3.
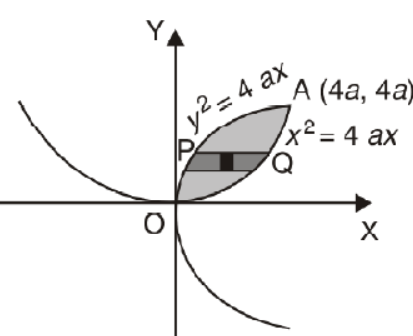
Example-2: Find the area between the parabola y ² = 4ax and another parabola x² = 4ay.
Sol. Let,
y² = 4ax ………………... (1)
and
x² = 4ay…………………. (2)
then if we solve these equations, we get the values of points where these two curves intersect
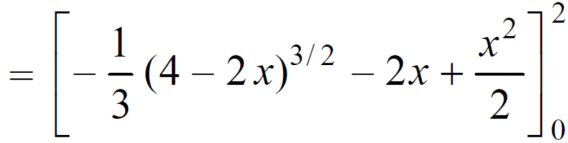
x varies from y²/4a to 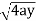 and y varies from o to 4a,
and y varies from o to 4a,
now using the concept of double integral,
Area = 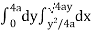
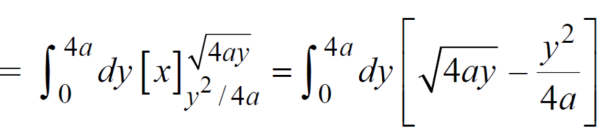
Area in polar coordinates-
Example-3: Find the area lying inside the cardioid r = a(1+cosθ) and outside the circle r = a, by using double integration.
Sol. We have,
r = a(1+cosθ) ……………………. (1)
and
r = a ………………………………. (2)
on solving these equations by eliminating r, we get
a(1+cosθ) = a
(1+cosθ) = 1
cosθ = 0
here a θ varies from – π/2 to π/2
limit of r will be a and 1+cosθ)
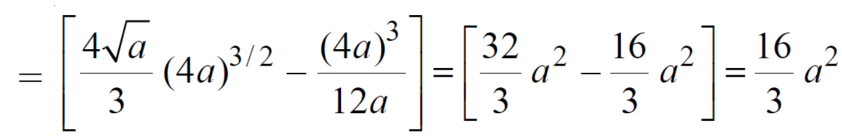
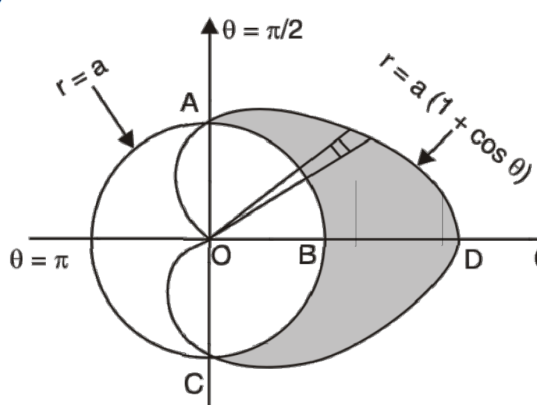
Which is the required area.
Example-4: Find the are lying inside a cardioid r = 1 + cosθ and outside the parabola r (1 + cosθ) = 1.
Sol. Let,
r = 1 + cosθ ……………………. (1)
r (1 + cosθ) = 1……………………. (2)
solving these equations, we get
(1 + cosθ) (1 + cosθ) = 1
(1 + cosθ) ² = 1
1 + cosθ = 1
cosθ = 0
θ = ±π / 2
so that, limits of r are,
1 + cosθ and 1 / 1 + cosθ
The area can be founded as below,
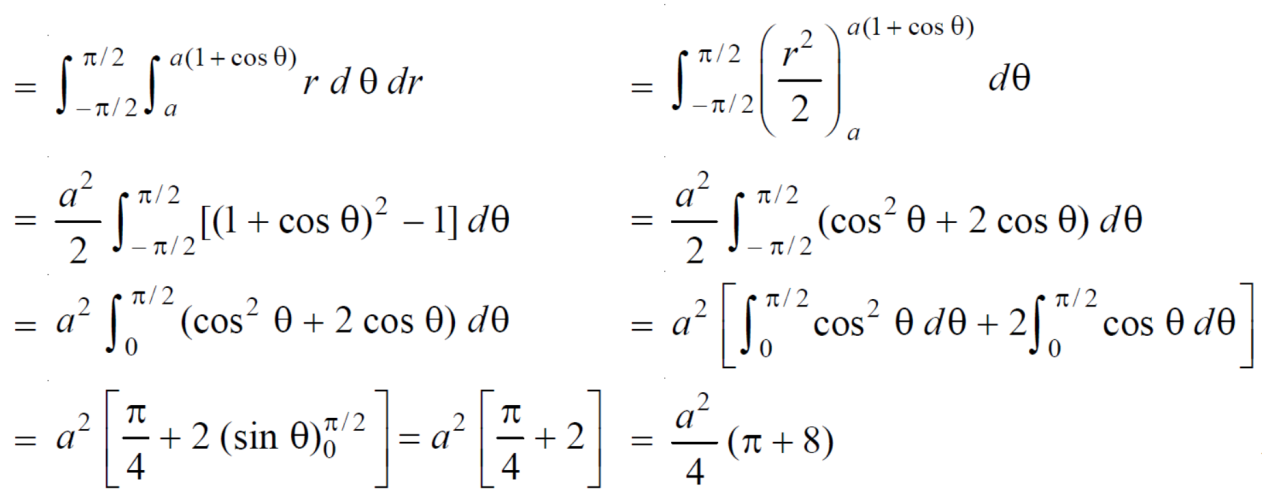
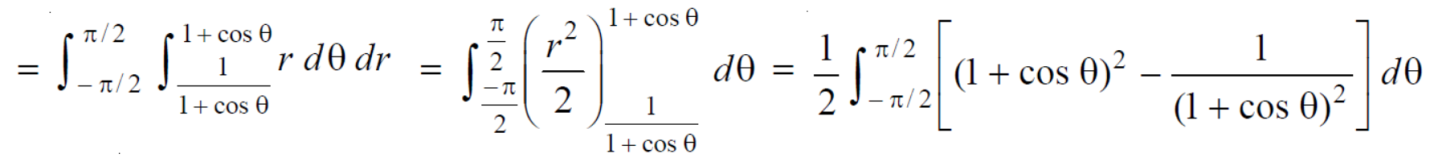
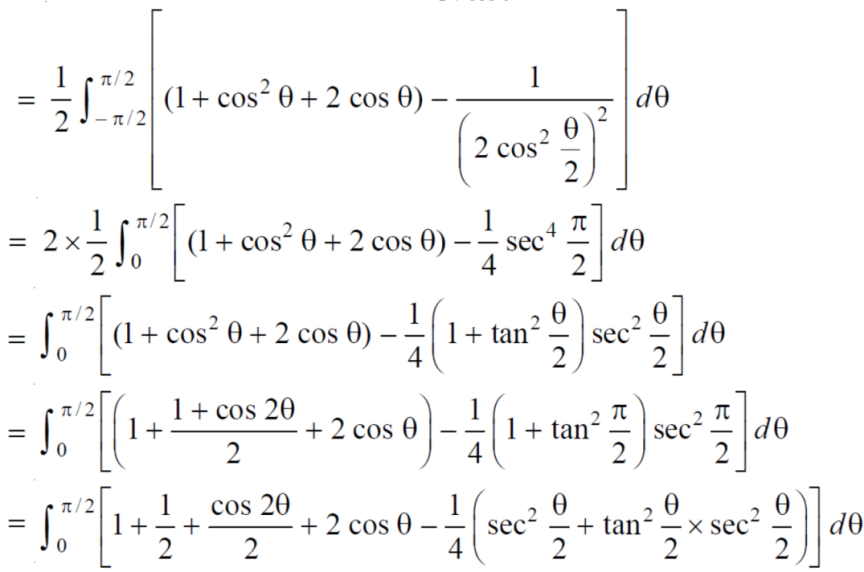
Double integrals as volumes
Suppose we have a curve y = f(x) is revolved about an axis, then a solid is generated, now we need to find out the volume of the solid generated,
The formula for volume of the solid generated about x-axis,
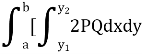
Example-1: Calculate the volume generated by the revolution of a cardioid,
r = a (1 – cosθ) about its axis
Sol. Here, r = a (1 – cosθ)
Volume =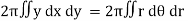
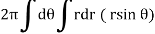
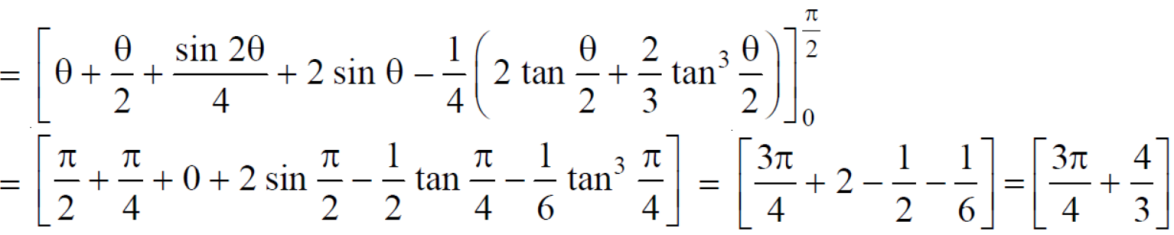
=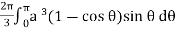
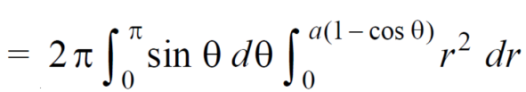
which is the volume of generated by cardioid.
Example-2: Find the volume generated by revolving a circle x ² + y² = 4 about the line x= 3.
Sol. We know that,
Volume = 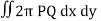
Here , PQ = 3 – x,
= 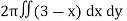
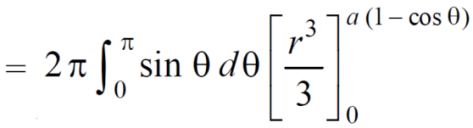
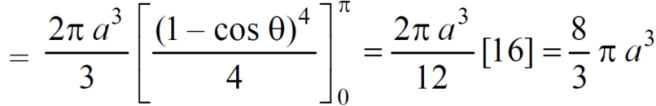
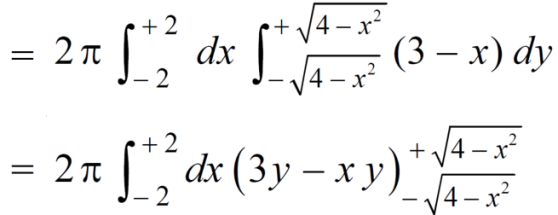
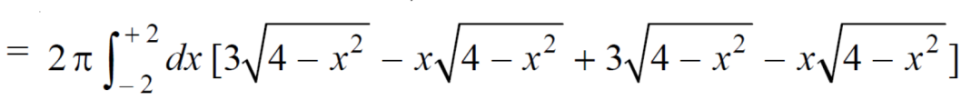
The volume is 24π².
Example-3: Calculate the volume under the surface z = 3 + x² - 2y over the region R defined as 0≤ x ≤ 1 and -x ≤ y ≤ x
Sol. The is a double integral of z = 3 + x² - 2y over the region R.
Volume will be,
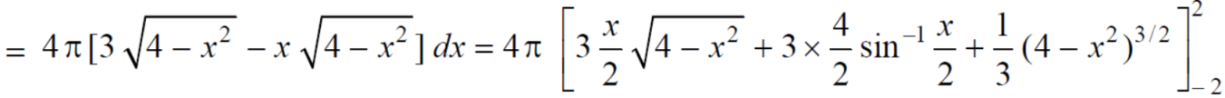
Definition: Let f(R.) be a function which is continuous at every point of the finite region (Volume V) of three-dimensional space. Divide the region V into n sub regions of respective volumes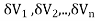 . Let (
. Let (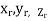 ) be a point in the
) be a point in the 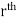 sub region then the sum:
sub region then the sum:
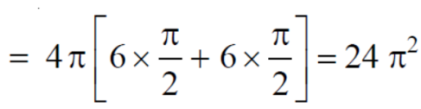 =
= 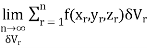
is called triple integration of f (x, y, z) over the region V provided limit on R.H.S of above Equation exists.
Example-1: Evaluate
Solution:
Let
I = 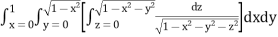
= 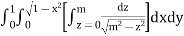
(Assuming m = 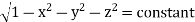 )
)
= 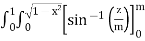 dxdy
dxdy
= 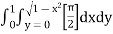
=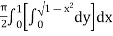
= 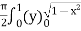 dx
dx
= 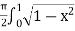 dx
dx
= 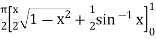
=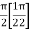
I =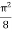
Example-2: Evaluate 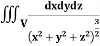 Where V is annulus between the spheres
Where V is annulus between the spheres 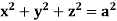 and
and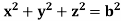 (
(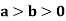 )
)
Solution: It is convenient to transform the triple integral into spherical polar co-ordinate by putting
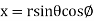 ,
, 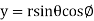 ,
, 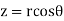
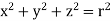 , dxdydz=
, dxdydz=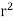 sin
sin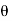 drd
drd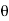 d
d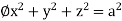 ,
,
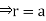 and
and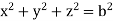
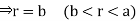
For the positive octant, r varies from r =b to r =a, 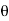 varies from
varies from 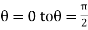 and
and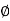 varies from
varies from 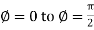
I= 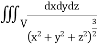
= 8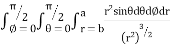
=8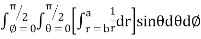
=8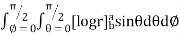
=8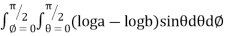
=8 log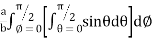
= 8 log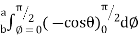
I= 8 log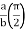
I = 4 log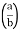
Example-3: Evaluate
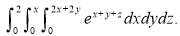
Solution: -
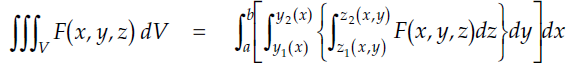
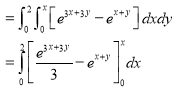
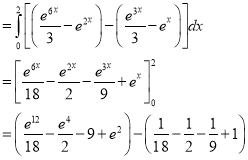
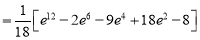
Ex.4: Evaluate-
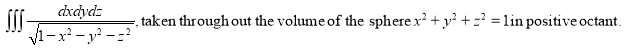
Solution: -
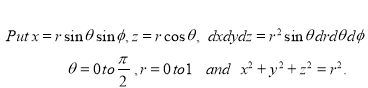
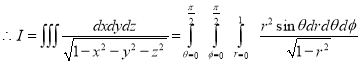
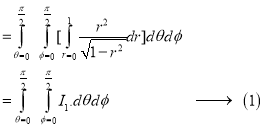
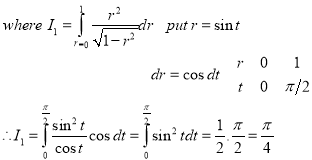
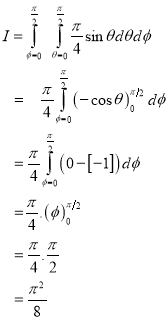
NOTES:
The volume of solid is given by
Volume =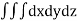
In Spherical polar system
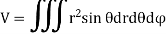
In cylindrical polar system
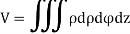
Ex.1: Find Volume of the tetrahedron bounded by the co-ordinate’s planes and the plane
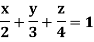
Solution: Volume =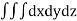 ………. (1)
………. (1)
Put 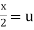 ,
, 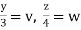
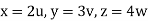
From equation (1) we have
V = 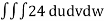
=24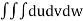
=24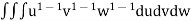 (u+v+w=1) By Dirichlet’s theorem.
(u+v+w=1) By Dirichlet’s theorem.
=24 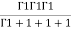
= =
=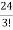 = 4
= 4
Volume =4
Ex.2: Find volume common to the cylinders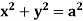 ,
,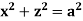 .
.
Solution: For given cylinders,
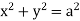 ,
, 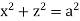 .
.
Z varies from
Z=-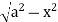 to z =
to z = 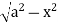
Y varies from
y= -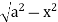 to y =
to y = 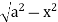
x varies from x= -a to x = a
By symmetry,
Required volume= 8 (volume in the first octant)
=8 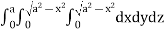
=8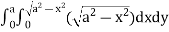
= 8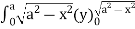 dx
dx
=8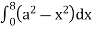
=8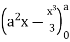
=8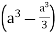
Volume = 16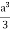
Ex.3: Evaluate
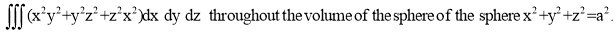
Solution: -
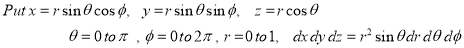
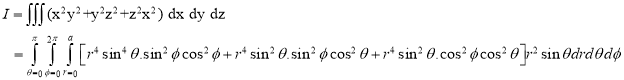
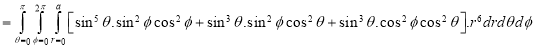
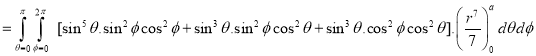
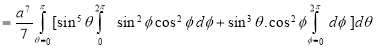
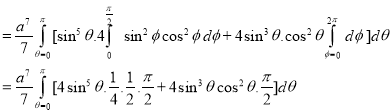
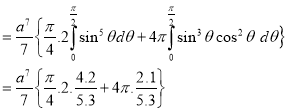
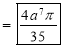
Ex.4: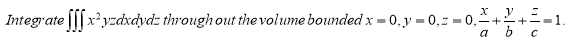
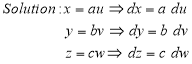
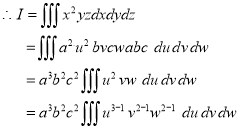
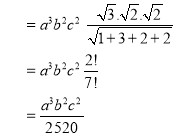
Ex.5:
Evaluate 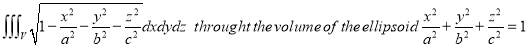
Solution: - Put
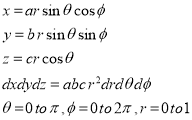
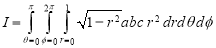
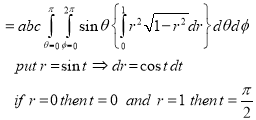
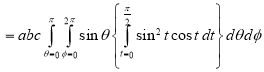
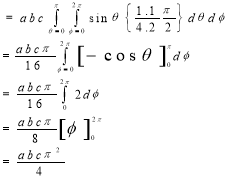
Key takeaways-
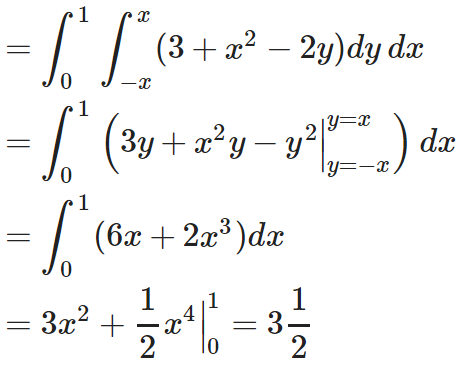
Volume =
3. In Spherical polar system
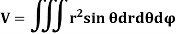
4. In cylindrical polar system
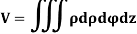
We can solve the double integration by changing independent variables.
Let the double integral is-
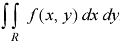
It’s to be changed by the new variables-u and v
The relationship between x, y and u, v is-
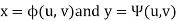
Then the double integration is converted into-
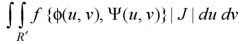
Where-
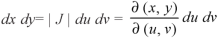
Example-: Evaluate-
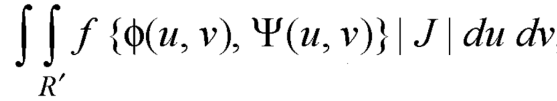
Where-
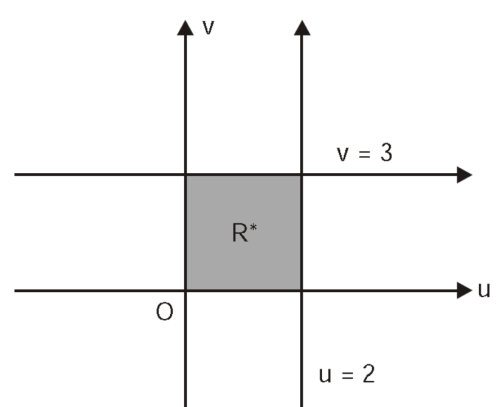
R is the region bounded by a parallelogram- x + y = 0, x + y = 2, 3x – 2y = 0, 3x – 2y = 3.
Sol.
By changing the variables x, y to the new variables u and v, by the substitution x + y = u, 3x – 2y = v, the given parallelogram R reduces to a rectangle 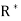
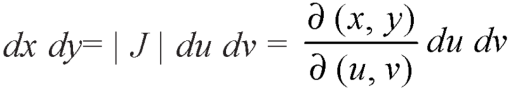
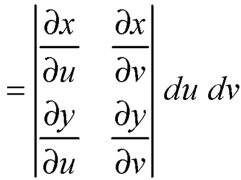
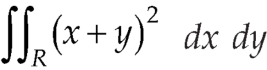
The required Jacobian is-
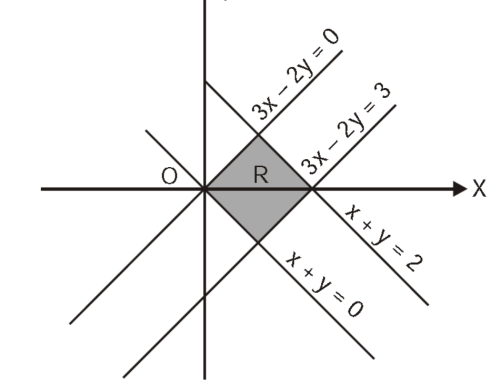
Since u = x + y and u = x + y = 2, here u varies from 0 to 2 while v varies from 0 to 3.
Since-
3x – 2y = v = 0, 3x – 2y = v = 3
Therefore, the integral will be in new variables-
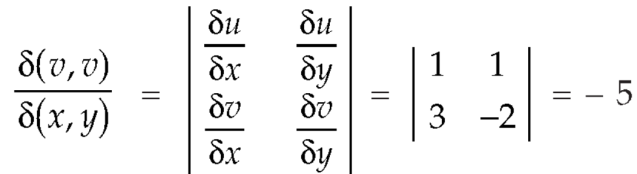
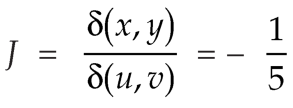
Which is the required answer.
Example: Evaluate 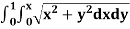 the transformation is x = v and y = uv.
the transformation is x = v and y = uv.
Sol.
Here the region of integration R is the triangle which is bounded by y = 0, x = 1 and y = x
Here put,
X = u and y = uv, we get-
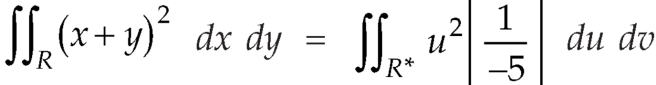
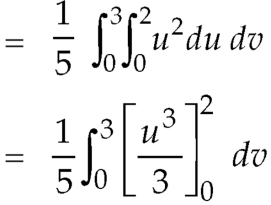
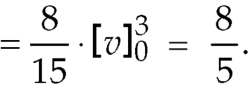
Here x varies from 0 to 1 while y varies from 0 to x.
Since u = x so u varies from 0 to 1
Here, similarly, since 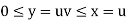 , so that v varies from 0 to 1. Thus-
, so that v varies from 0 to 1. Thus-
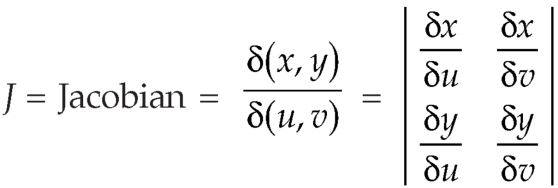
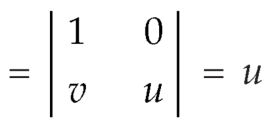
Beta and Gamma functions-
The beta and gamma functions are defined as-
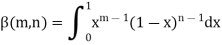
And
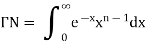
These integrals are also known as first and second Eulerian integrals.
Note- Beta function is symmetrical with respect to m and n.
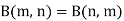
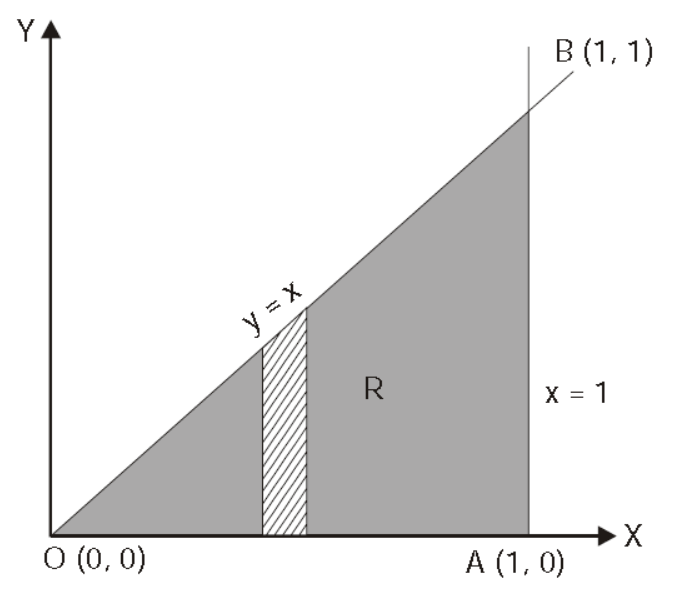
Some important results-
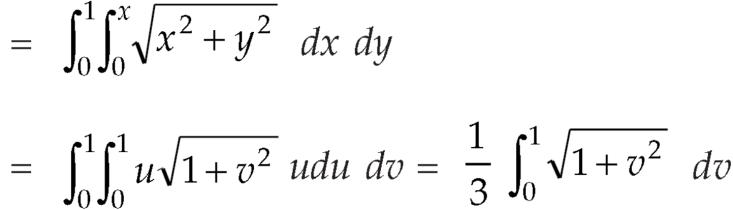
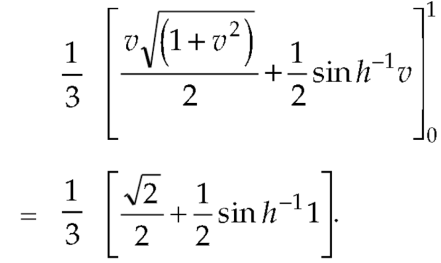
Ex.1: Evaluate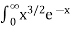 dx
dx
Solution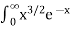 dx =
dx = 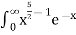 dx
dx
= Γ (5/2)
= Γ (3/2+ 1)
= 3/2 Γ (3/2)
= 3/2. ½ Γ (½)
= 3/2. ½ π
= ¾ π
Ex. 2: Find γ(-½)
Solution:
(-½) + 1= ½
Γ (-1/2) = Γ (-½ + 1) / (-½)
= - 2 Γ (1/2)
= - 2 π
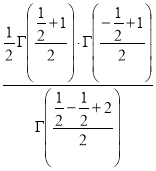
Ex3. Show that 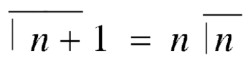
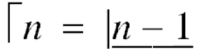
Solution:
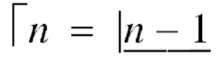 =
= 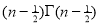
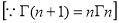
= 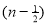
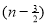
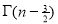
= 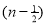
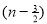
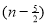
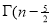 ) .......................
) .......................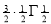
= 
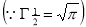
= 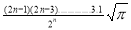
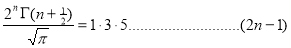
Ex. 4: Evaluate 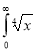
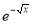 dx.
dx.
Solution: Let 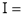
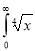
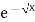 dx
dx
X | 0 |
|
t | 0 |
|
Put 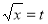 or
or 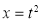 ;dx
;dx
=2t dt
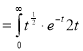 dt
dt
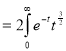 dt
dt
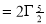
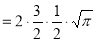
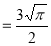
Ex. 5: Evaluate 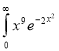 dx.
dx.
Solution: Let 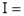
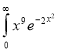 dx.
dx.
Put 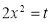 or
or 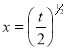 ; 4x dx = dt
; 4x dx = dt
x | 0 |
|
t | 0 |
|
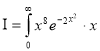 dx
dx
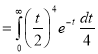
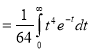
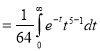
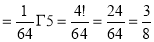
Evaluation of beta function 𝛃 (m, n)-
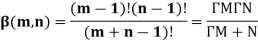
Here we have-
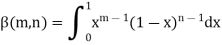
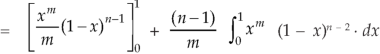
Or
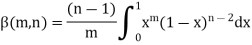
Again, integrate by parts, we get-
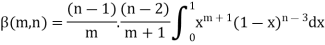
Repeating the process above, integrating by parts we get-
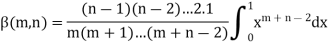
Or
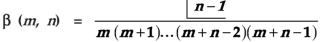
Evaluation of gamma function-
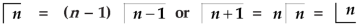
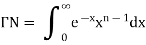
Integrating by parts, we take 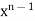 as first function-
as first function-
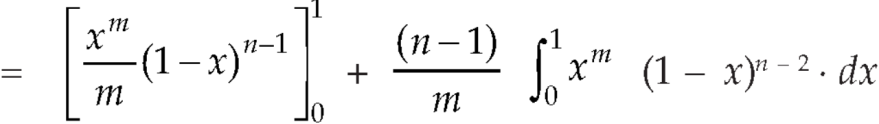
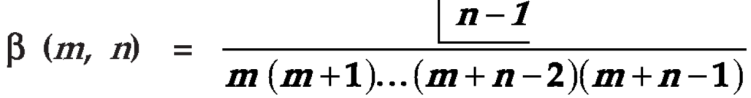

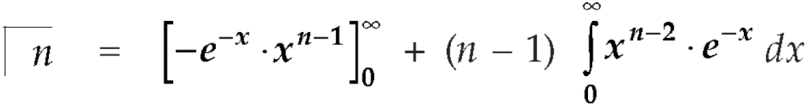
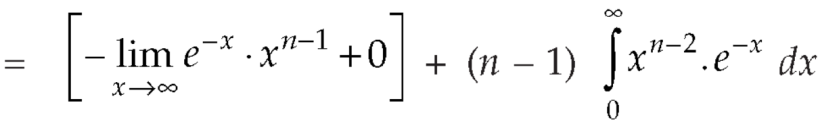
We get-
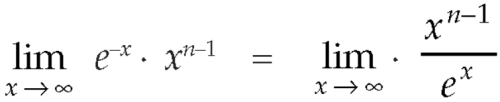
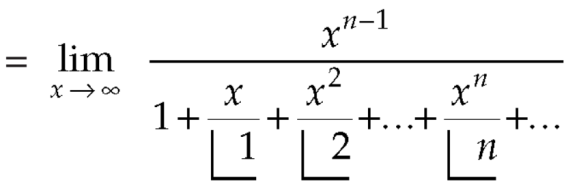
Replace n by n+1,
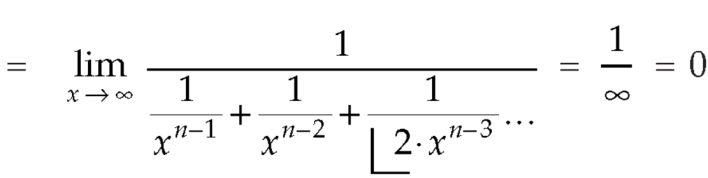
Relation between beta and gamma function-
We know that-
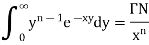
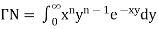 ………… (1)
………… (1)
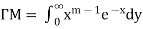 …………………. (2)
…………………. (2)
Multiply equation (1) by 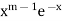 , we get-
, we get-
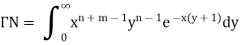
Integrate both sides with respect to x within limits x = 0 to x =  , we get-
, we get-
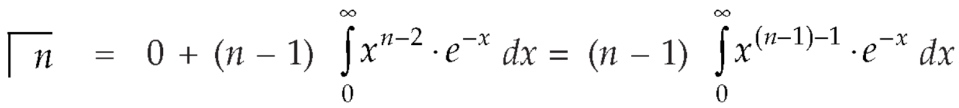
But
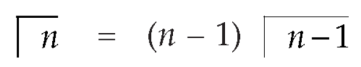
By putting λ = 1 + y and n = m + n
We get by using this result in (2)-
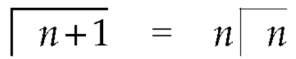
So that-
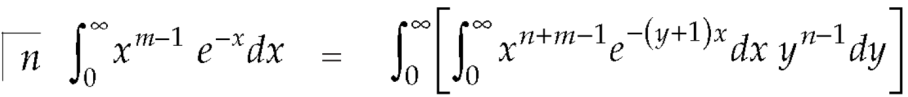
Definition: Beta function
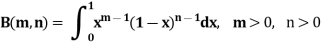
Properties of Beta function:
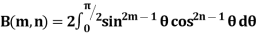
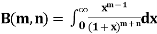

Example (1): Evaluate I = 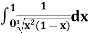
Solution:
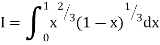
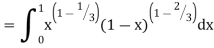
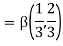
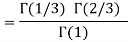
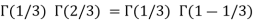
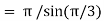
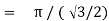
= 2 π/3
Example (2): Evaluate: I = 02 x2 / (2 – x) . dx
Solution:
Letting x = 2y, we get
I = (8/2) 01 y2 (1 – y) -1/2dy
= (8/2). B (3, 1/2)
= 642 /15
BETA FUNCTION MORE PROBLEMS
Relation between Beta and Gamma functions:
Example (1): Evaluate: I = 0a x4 (a2 – x2 ) . dx Solution: Letting x2 = a2 y, we get I = (a6 / 2) 01 y 3/2 (1 – y )1/2dy = (a6 / 2). B (5/2, 3/2) = a6 /3 2 Example (2): Evaluate: I = 02 x (8 – x3 ) . dx Solution: Let x3 = 8y I = (8/3) 01 y-1/3 (1 – y) 1/3. dy = (8/3) B (2/3, 4/3) = 16 π / (9 3) | ||||||
Example (3): Prove that Solution: Let Put
Example (4): Evaluate Solution: Let Put When
Also
Example (5): Show that Solution: =
Key takeaways-
Where
|
2. if a function f: [a, b] →R is continuous, then the function ‘f’ is always Integrable.
3. Let f is function defined on [a, ∞) and it is integrable on [a, t] for all t >a, then
4. If 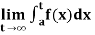 exists, then we define the improper integral of f over [a, ∞) as follows-
exists, then we define the improper integral of f over [a, ∞) as follows-
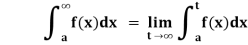
5. The beta and gamma functions are defined as-
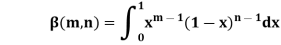
And
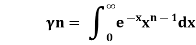
These integrals are also known as first and second Eulerian integrals.
6. Beta function is symmetrical with respect to m and n.
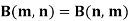
References: