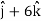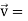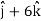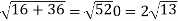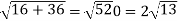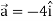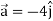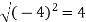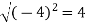Unit - 4
Vector calculus
Vector function-
Suppose 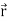 be a function of a scalar variable t, then-
be a function of a scalar variable t, then-
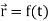
Here vector 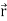 varies corresponding to the variation of a scalar variable t that its length and direction be known as value of t is given.
varies corresponding to the variation of a scalar variable t that its length and direction be known as value of t is given.
Any vector 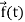 can be expressed as-
can be expressed as-
Here  ,
,  ,
, 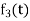 are the scalar functions of t.
are the scalar functions of t.
Differentiation of a vector-

We can denote it as- 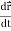
Similarly, 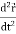 is the second order derivative of
is the second order derivative of 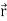
Note- 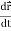 gives the velocity and
gives the velocity and 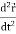 gives acceleration.
gives acceleration.
Note-
1. Velocity = 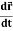
2. Acceleration = 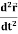
The derivative of the velocity vector V(t) is called acceleration A(t), and it is given as-
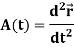
Rules for differentiation-
1. 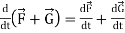
2. 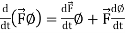
3. 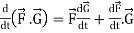
4. 
5. 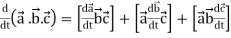
Example-1: A particle moves along the curve 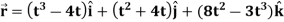 , here ‘t’ is the time. Find its velocity and acceleration at t = 2.
, here ‘t’ is the time. Find its velocity and acceleration at t = 2.
Sol. Here we have-
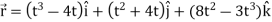
Then, velocity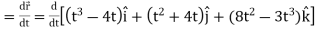
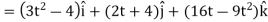
Velocity at t = 2,
= 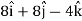
Acceleration = 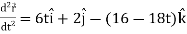
Acceleration at t = 2,
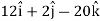
Example-2: If 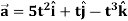 and
and 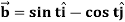 then find-
then find-
1. 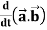
2. 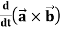
Sol. 1. We know that-
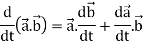
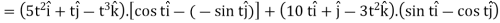
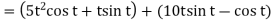
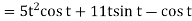
2.

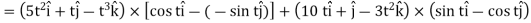
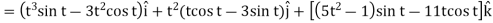
Example-3: A particle is moving along the curve x = 4 cos t, y = 4 sin t, z = 6t. then find the velocity and acceleration at time t = 0 and t = π/2.
And find the magnitudes of the velocity and acceleration at time t.
Sol. suppose 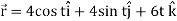
Now,
At t = 0 |
|
At t = π/2 |
|
At t = 0 | |v|= |
At t = π/2 | |v|= |
Again acceleration-
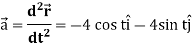
Now-
At t = 0 |
|
At t = π/2 |
|
At t = 0 | |a|= |
At t = π/2 | |a|= |
Key takeaways-
1. Any vector  can be expressed as-
can be expressed as-
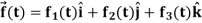
Here 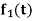 ,
, 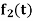 ,
, 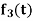 are the scalar functions of t.
are the scalar functions of t.
2. Velocity = 
3. Acceleration = 
Scalar point function-
If for each point P of a region R, there corresponds a scalar denoted by f(P), in that case f is called scalar point function of the region R.
Note-
Scalar field- this is a region in space such that for every point P in this region, the scalar function ‘f’ associates a scalar f(P).
Vector point function-
If for each point P of a region R, then there corresponds a vector  then
then  is called a vector point function for the region R.
is called a vector point function for the region R.
Vector field-
Vector filed is a reason in space such that with every point P in the region, the vector function  associates a vector
associates a vector  (P).
(P).
Note-
Del operator-
The del operated is defined as-
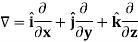
Example: show that 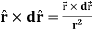 where
where 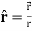
Sol. here it is given-
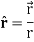
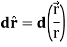
= 
Therefore-

Note-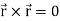
Hence proved
Gradient-
The vector differential operator is written as-
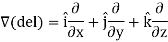
Gradient
Suppose f (x, y, z) be the scalar function and it is continuously differentiable then the vector-
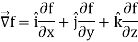
Is called gradient of f and we can write is as grad f.
So that-
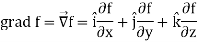
Here 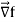 is a vector which has three components
is a vector which has three components 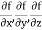
Properties of gradient-
Property-1: 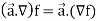
Proof:
First, we will take left hand side
L.H.S = 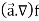
= 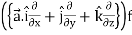
= 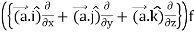
= 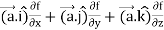
Now taking R.H.S,
R.H.S. = 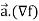
= 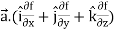
= 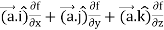
Here- L.H.S. = R.H.S.
Hence proved.
Property-2: Gradient of a constant (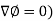
Proof:
Suppose 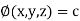
Then 
We know that the gradient-
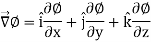
= 0
Property-3: Gradient of the sum and difference of two functions-
If f and g are two scalar point functions, then
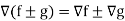
Proof:
L.H.S 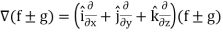
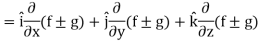
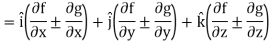
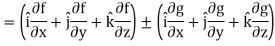
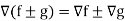
Hence proved
Property-4: Gradient of the product of two functions
If f and g are two scalar point functions, then
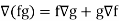
Proof:
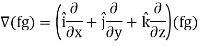
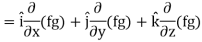
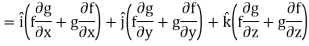
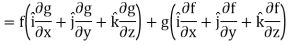
So that-

Hence proved.
Property-5: Gradient of the quotient of two functions-
If f and g are two scalar point functions, then-
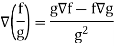
Proof:
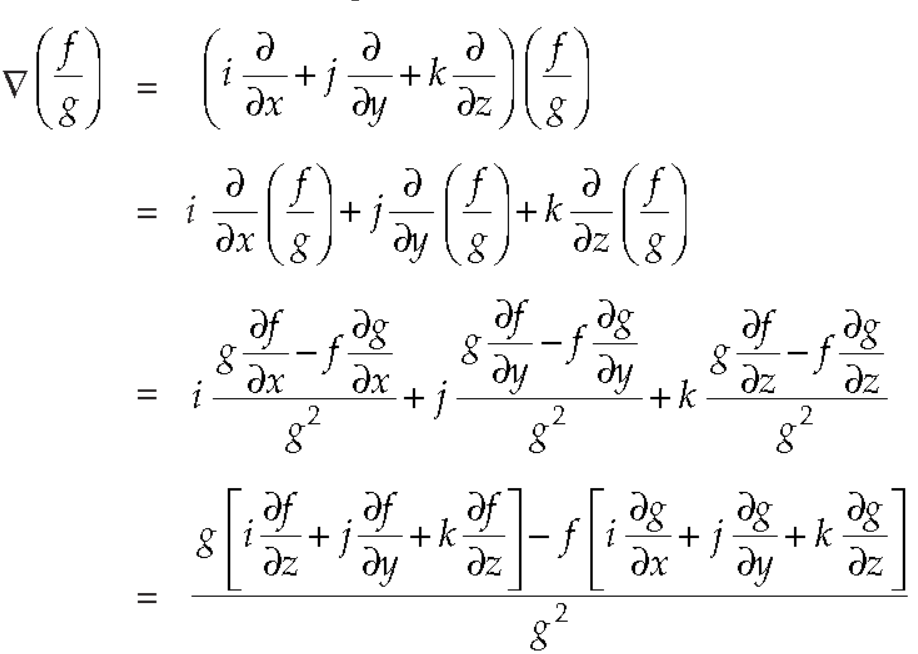
So that-

Example-1: If 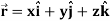 , then show that
, then show that
1. 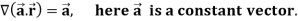
2. 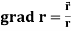
Sol.
Suppose 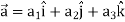 and
and 

Now taking L.H.S,
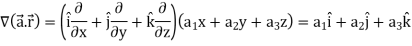
Which is 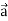
Hence proved.
2. 
So that
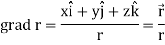
Example: If 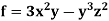 then find grad f at the point (1, -2, -1).
then find grad f at the point (1, -2, -1).
Sol.
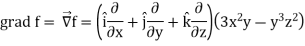
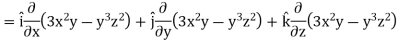

Now grad f at (1, -2, -1) will be-
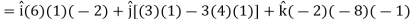
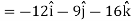
Example: If 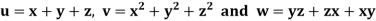 then prove that grad u, grad v and grad w are coplanar.
then prove that grad u, grad v and grad w are coplanar.
Sol.
Here- 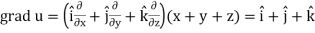
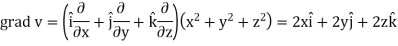

Now-

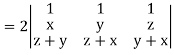
Apply 

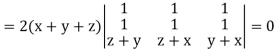
Which becomes zero.
So that we can say that grad u, grad v and grad w are coplanar vectors.
Directional derivative-
Let ϕ be a scalar point function and let ϕ(P) and ϕ(Q) be the values of ϕ at two neighbouring points P and Q in the field. Then,
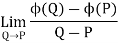
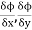 ,
,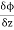 are the directional derivative of ϕ in the direction of the coordinate axes at P.
are the directional derivative of ϕ in the direction of the coordinate axes at P.
The directional derivative of ϕ in the direction l, m, n= l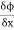 + m
+ m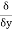 +
+ 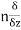
The directional derivative of ϕ in the direction of 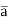 =
= 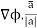
Example: Find the directional derivative of 1/r in the direction 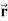 where
where 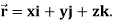
Sol. Here 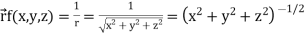
Now,
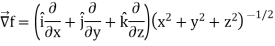
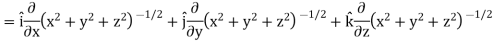
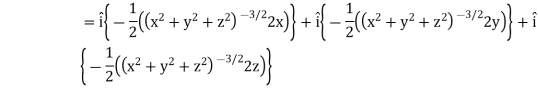
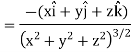
And 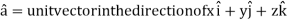
We know that-
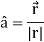
So that-

Now,
Directional derivative-
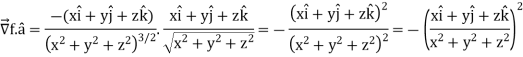
Example: Find the directional derivative of

At the points (3, 1, 2) in the direction of the vector 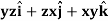 .
.
Sol. Here it is given that-
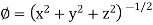
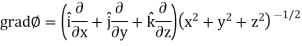
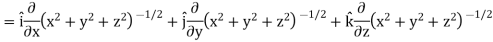
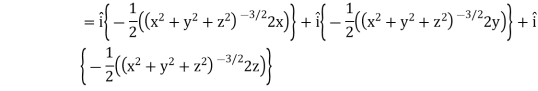
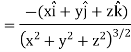
Now at the point (3, 1, 2)-
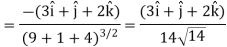
Let 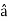 be the unit vector in the given direction, then
be the unit vector in the given direction, then
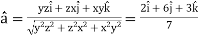 at (3, 1, 2)
at (3, 1, 2)
Now,
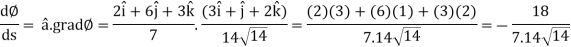
Example: Find the directional derivatives of  at the point P (1, 1, 1) in the direction of the line
at the point P (1, 1, 1) in the direction of the line 
Sol. Here
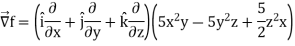
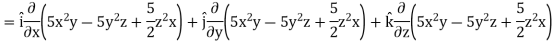

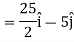
Direction ratio of the line 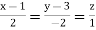 are 2, -2, 1
are 2, -2, 1
Now directions cosines of the line are-
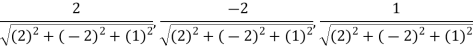
Which are 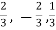
Directional derivative in the direction of the line-

Key takeaways-
1. Scalar field- this is a region in space such that for every point P in this region, the scalar function ‘f’ associates a scalar f(P).
2. Vector field-
Vector filed is a reason in space such that with every point P in the region, the vector function 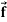 associates a vector
associates a vector 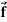 (P).
(P).
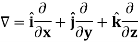
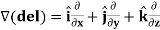
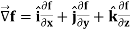
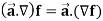
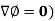
Divergence (Definition)-
Suppose 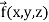 is a given continuous differentiable vector function then the divergence of this function can be defined as-
is a given continuous differentiable vector function then the divergence of this function can be defined as-

Curl (Definition)-
Curl of a vector function can be defined as-
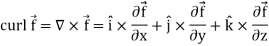
Note- Irrotational vector-
If 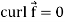 then the vector is said to be irrotational.
then the vector is said to be irrotational.
Vector identities:
Identity-1: grad uv = u grad v + v grad u
Proof:
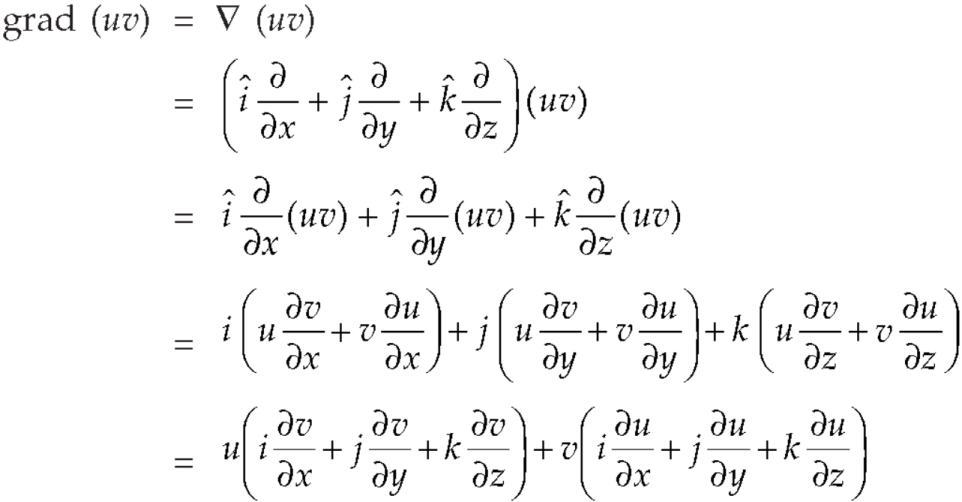
So that
grad uv = u grad v + v grad u
Identity-2: 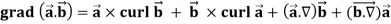
Proof:
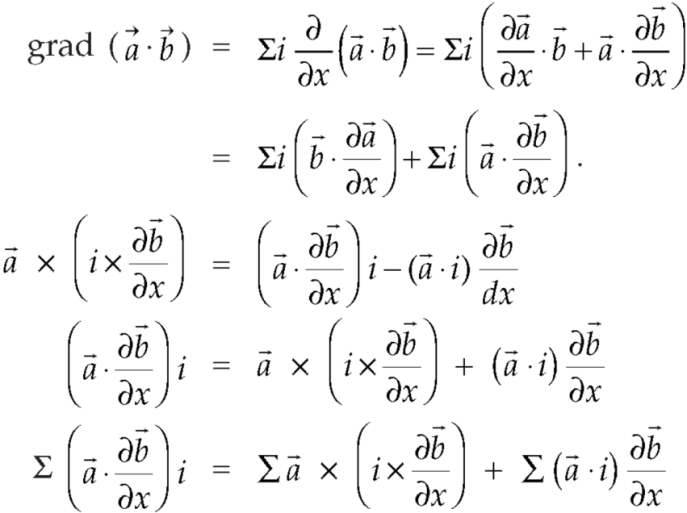

Interchanging 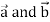 , we get-
, we get-
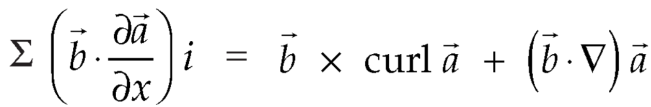
We get by using above equations-
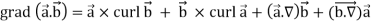
Identity-3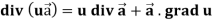
Proof: 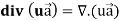
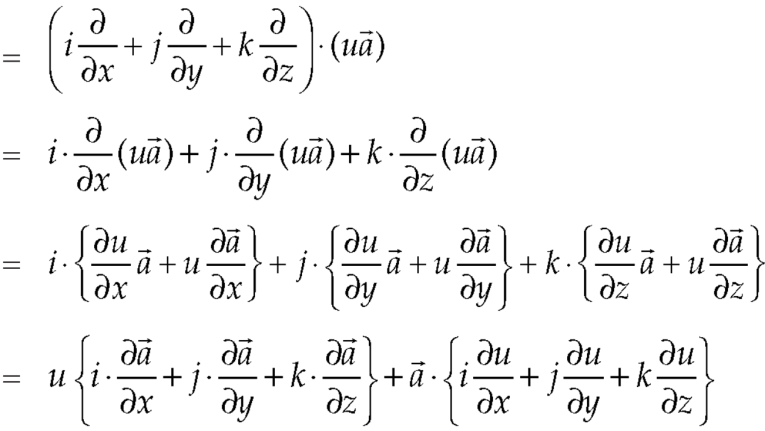
So that-
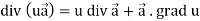
Identity-4
Proof:
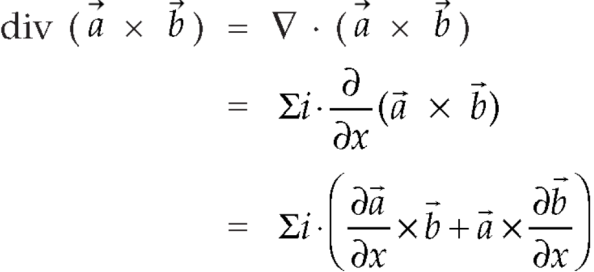
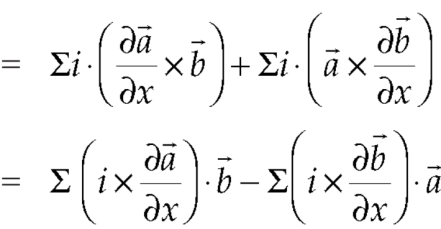
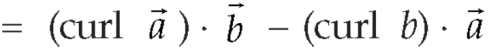
So that,
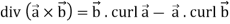
Identity-5 curl (u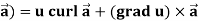
Proof:
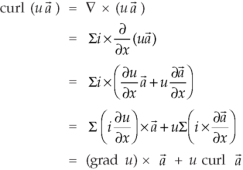
So that
curl (u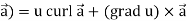
Identity-6: 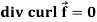
Proof:
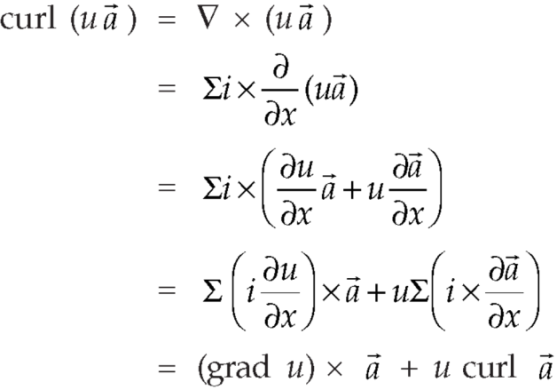
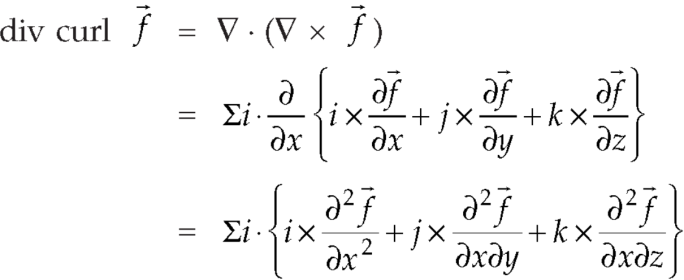
So that-
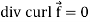
Identity-7: 
Proof:
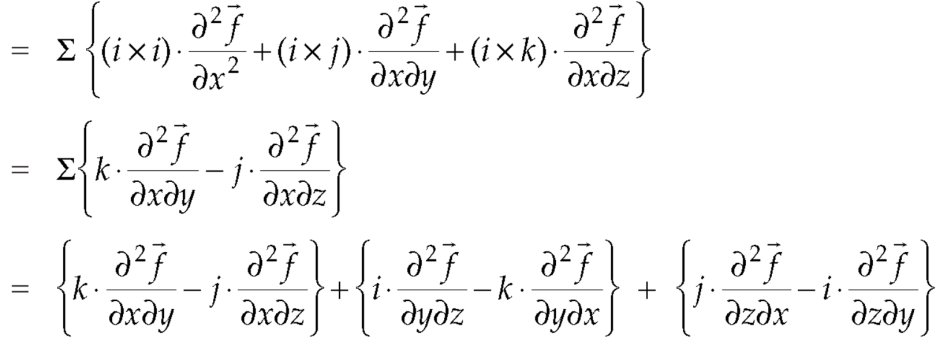
So that-
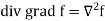
Example-1: Show that-
1. 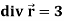
2.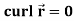
Sol. We know that-
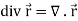

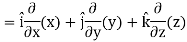

2. We know that-
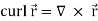


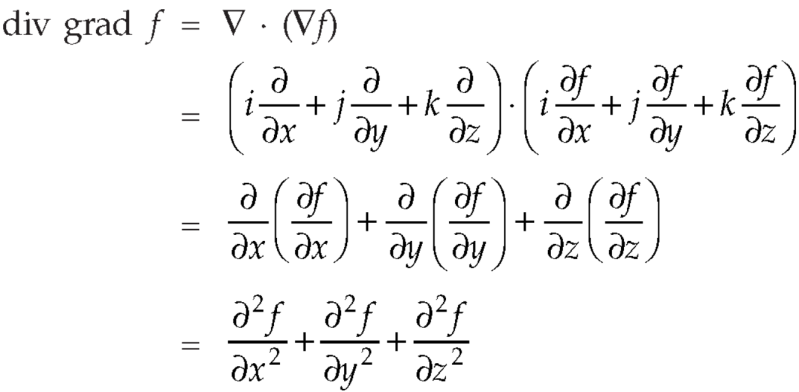
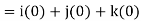 = 0
= 0
Example-2: If  then find the divergence and curl of
then find the divergence and curl of 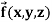 .
.
Sol. we know that-
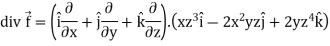
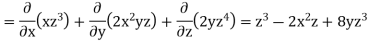
Now-
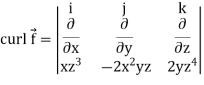
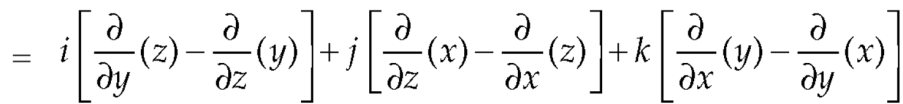
Example-3: Prove that 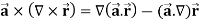
Note- here 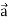 is a constant vector and
is a constant vector and 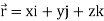
Sol. here  and
and 
So that
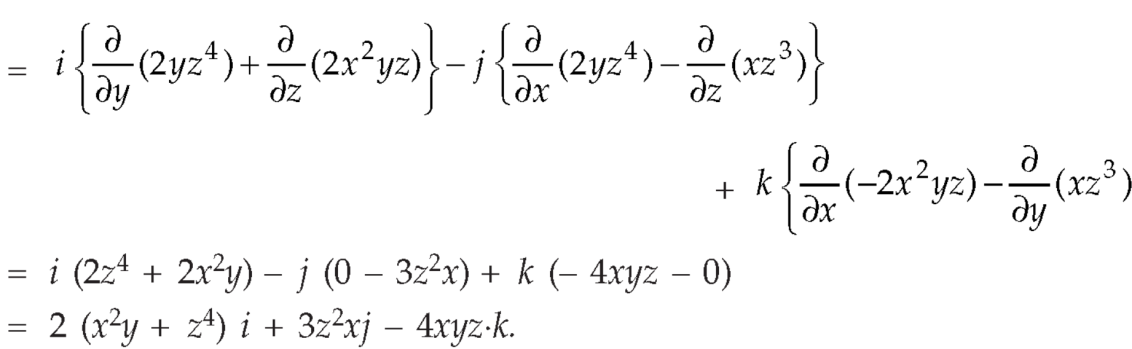
Now-
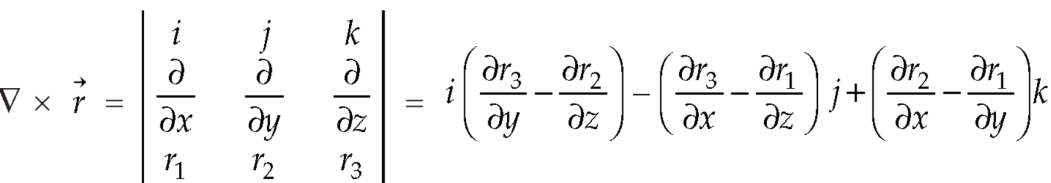
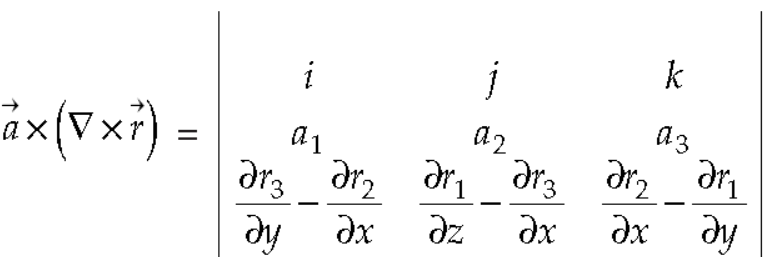

So that-
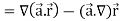
Key takeaways-
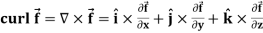
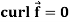
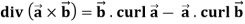
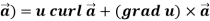
The Line Integral
Let- F be vector function defined throughout some region of space and let C be any curve in that region. ṝ is the position vector of a point p (x, y, z) on C then the integral ƪ F. dṝ is called the line integral of F taken over
Now, since ṝ =xi+yi+zk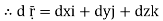
And if F͞ =F1i + F2 j+ F3 K
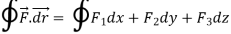
Q1. Evaluate 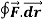 where F= cos y.i-x siny j and C is the curve y=
where F= cos y.i-x siny j and C is the curve y=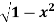 in the xy plae from (1,0) to (0,1)
in the xy plae from (1,0) to (0,1)
Solution: The curve y=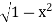 i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
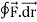 =
= 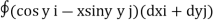
= 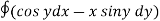
= =-1
=-1
Q2. Evaluate  where
where 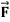 = (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
= (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
Solution: F x dr = 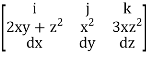
Put x=t, y=t2, z= t3
Dx=dt, dy=2tdt, dz=3t2dt.
F x dr = 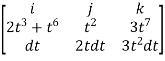
=(3t4-6t8) dti – (6t5+3t8 -3t7) dt j +( 4t4+2t7-t2) dt k
=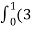 t4-6t3) dti –(6t5+3t8-3t7) dt j+(4t4 + 2t7 – t2) dt k
t4-6t3) dti –(6t5+3t8-3t7) dt j+(4t4 + 2t7 – t2) dt k
=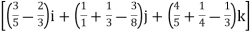
=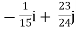 +
+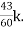
Example 3: Prove that ͞͞͞F = [y2cos x +z3] i+(2y sin x – 4) j +(3xz2 + 2) k is a conservative field. Find (i) scalar potential for͞͞͞F (ii) the work done in moving an object in this field from (0, 1, -1) to (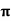 / 2, -1, 2)
/ 2, -1, 2)
 Sol.: (a) The field is conservative if cur͞͞͞͞͞͞F = 0.
Sol.: (a) The field is conservative if cur͞͞͞͞͞͞F = 0.
 Now, curl͞͞͞ F =
Now, curl͞͞͞ F = 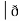 ̷̷
̷̷ X
X 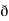 /
/ 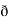 y
y 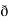 /
/  z
z
Y2COS X +Z3 2y sin x-4 3xz2 + 2
; Cur 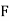 = (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
= (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
; F is conservative.
(b) Since F is conservative there exists a scalar potential ȸ such that
F = ȸ
 (y2cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k =
(y2cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k = 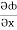 i +
i + 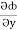 j +
j + 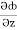 k
k
 = y2cos x + z3,
= y2cos x + z3, 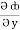 = 2y sin x – 4,
= 2y sin x – 4, 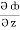 = 3xz2 + 2
= 3xz2 + 2
Now,  =
= 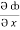 dx +
dx + 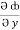 dy +
dy + 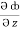 dz
dz
= (y2cos x + z3) dx +(2y sin x – 4) dy + (3xz2 + 2) dz
= (y2cos x dx + 2y sin x dy) +(z3dx +3xz2dz) +(- 4 dy) + (2 dz)
=d (y2 sin x + z3x – 4y -2z)
 ȸ = y2 sin x +z3x – 4y -2z
ȸ = y2 sin x +z3x – 4y -2z
(c) now, work done =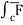 .d ͞r
.d ͞r
= 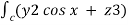 dx + (2y sin x – 4) dy + (3xz2 + 2) dz
dx + (2y sin x – 4) dy + (3xz2 + 2) dz
= 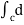 (y2 sin x + z3x – 4y + 2z) (as shown above)
(y2 sin x + z3x – 4y + 2z) (as shown above)
= [ y2 sin x + z3x – 4y + 2z] ( 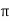 /2, -1, 2)
/2, -1, 2)
= [ 1 +8  + 4 + 4] – { - 4 – 2} =4
+ 4 + 4] – { - 4 – 2} =4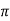 + 15
+ 15
Sums Based on Line Integral
1. Evaluate 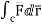 where
where 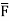 =yz i+zx j+xy k and C is the position of the curve.
=yz i+zx j+xy k and C is the position of the curve.
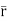 = (a cost) i+(b sint) j+ct k, from y=0 to t=π/4.
= (a cost) i+(b sint) j+ct k, from y=0 to t=π/4.
Soln. 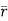 = (a cost) i+ (b sint) j+ct k
= (a cost) i+ (b sint) j+ct k
The parametric eqn. of the curve is x= a cost, y=b sint, z=ct (i)
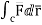 =
=
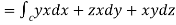
Putting values of x, y, z from (i),
dx=-a sint
dy=b cost
dz=c dt
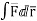 =
=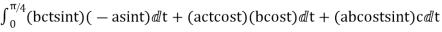
=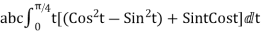
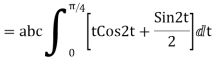
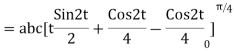
=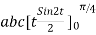 =
= 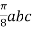
2. Find the circulation of 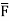 around the curve C where
around the curve C where 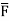 =yi+zj+xk and C is circle
=yi+zj+xk and C is circle  .
.
Soln. Parametric eqn of circle are:
x=a cos
y=a sin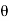
z=0
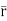 =xi+yj+zk = a cos
=xi+yj+zk = a cos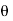 i + b cos
i + b cos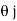 + 0 k
+ 0 k
d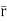 = (-a sin
= (-a sin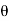 i + a cos
i + a cos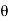 j) d
j) d
Circulation =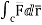 =
=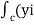 +zj+xk). d
+zj+xk). d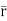
=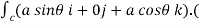 -a sin
-a sin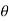 i + a cos
i + a cos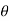 j) d
j) d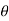
=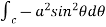 =
= 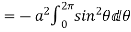


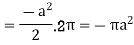
Surface integrals-
An integral which we evaluate over a surface is called a surface integral.
Surface integral = 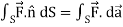
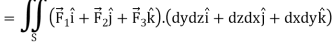
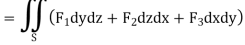
Volume integrals-
The volume integral is denoted by 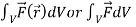
And defined as-
If  , then
, then
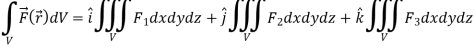
Note-
If in a conservative field 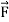

Then this is the condition for independence of path.
Example: Evaluate 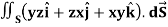 , where S is the surface of the sphere
, where S is the surface of the sphere 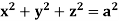 in the first octant.
in the first octant.
Sol. Here-
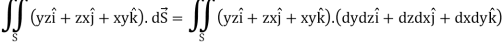
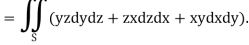
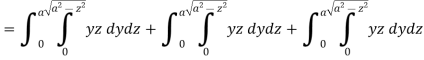
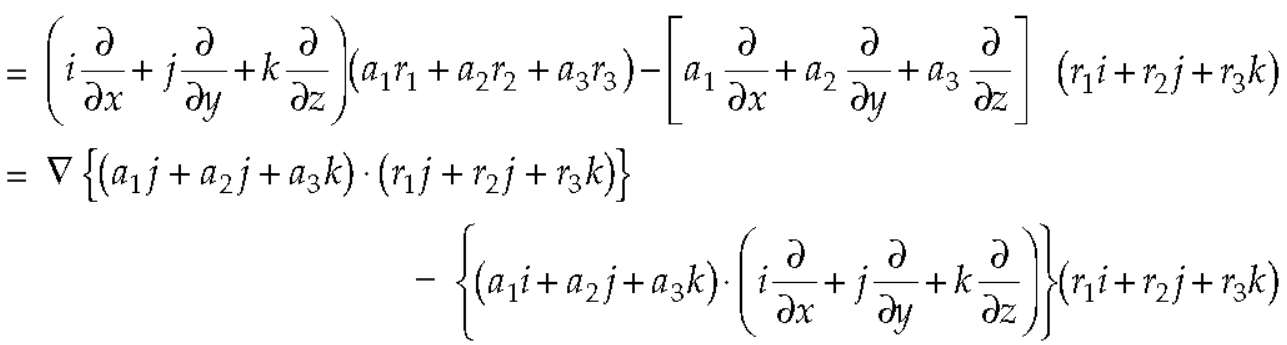
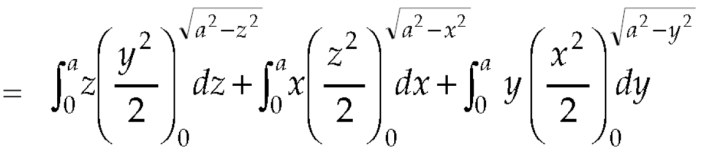
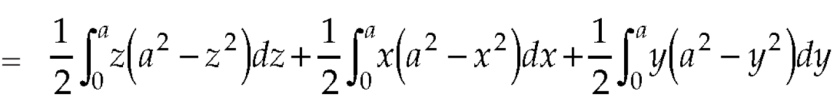
Which becomes-
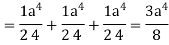
Example: Evaluate  , where
, where 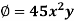 and V is the closed reason bounded by the planes 4x + 2y + z = 8, x = 0, y = 0, z = 0.
and V is the closed reason bounded by the planes 4x + 2y + z = 8, x = 0, y = 0, z = 0.
Sol.
Here- 4x + 2y + z = 8
Put y = 0 and z = 0 in this, we get
4x = 8 or x = 2
Limit of x varies from 0 to 2 and y varies from 0 to 4 – 2x
And z varies from 0 to 8 – 4x – 2y
So that-
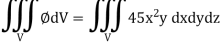
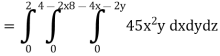

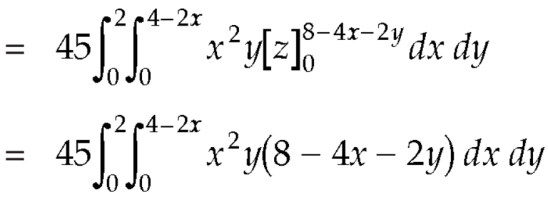

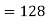
So that-
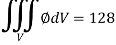
Example: Evaluate  if V is the region in the first octant bounded by
if V is the region in the first octant bounded by 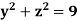 and the plane x = 2 and
and the plane x = 2 and 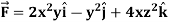 .
.
Sol.
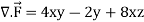
x varies from 0 to 2
The volume will be-
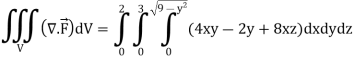
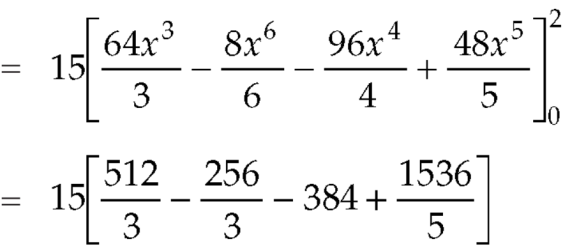
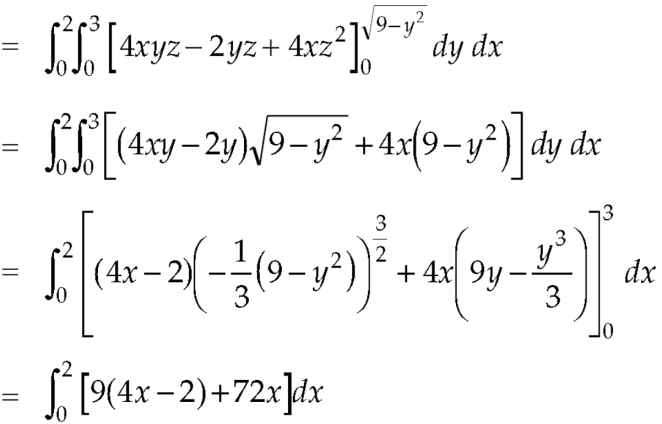
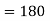
Key takeaways-
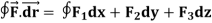
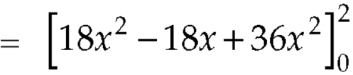

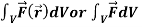
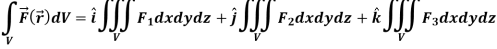
5. If in a conservative field 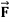
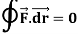
Then this is the condition for independence of path
Stoke’s theorem (without proofs) and their verification-
If  is any continuously differentiable vector point function and S is a surface bounded by a curve C, then-
is any continuously differentiable vector point function and S is a surface bounded by a curve C, then-
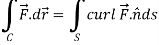
Example-1: Verify stoke’s theorem when 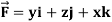 and surface S is the part of sphere
and surface S is the part of sphere 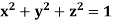 , above the xy-plane.
, above the xy-plane.
Sol.
We know that by stoke’s theorem,

Here C is the unit circle- 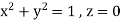
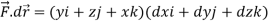

So that-

Now again on the unit circle C, z = 0
dz = 0
Suppose, 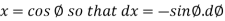
And 
Now
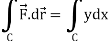
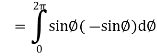
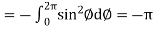 ……………… (1)
……………… (1)
Now-
Curl 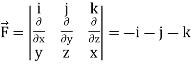
Using spherical polar coordinates-
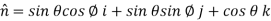
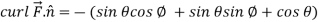
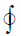
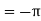 ………………… (2)
………………… (2)
From equation (1) and (2), stoke’s theorem is verified.
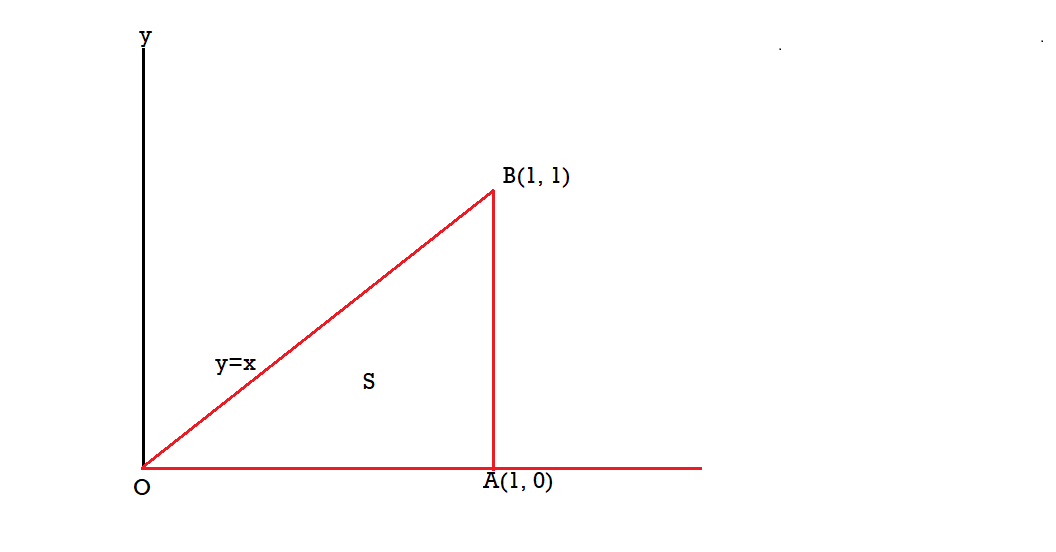
Example-2: If  and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate
and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate 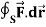 by using Stoke’s theorem.
by using Stoke’s theorem.
Sol. here we see that z-coordinates of each vertex of the triangle is zero, so that the triangle lies in the xy-plane and 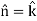
Now,
Curl 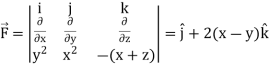
Curl 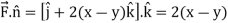
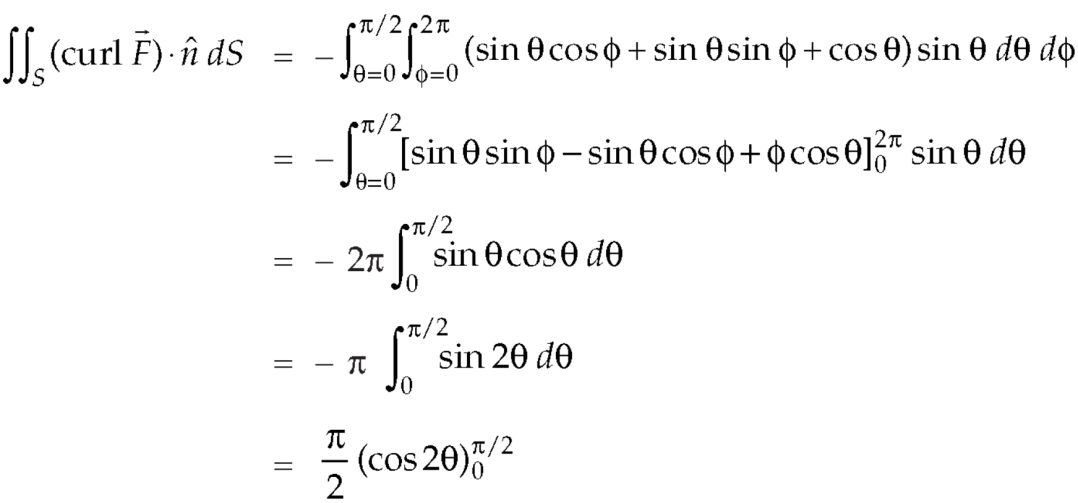
The equation of the line OB is y = x
Now by stoke’s theorem,
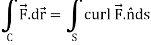

Example-3: Verify Stoke’s theorem for the given function-
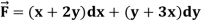
Where C is the unit circle in the xy-plane.
Sol. Suppose-
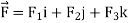
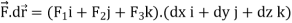
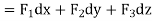
Here 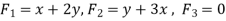
We know that unit circle in xy-plane-
Or
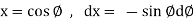
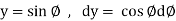
So that,
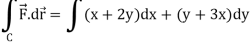
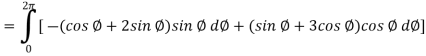
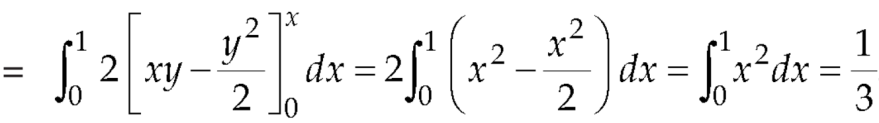
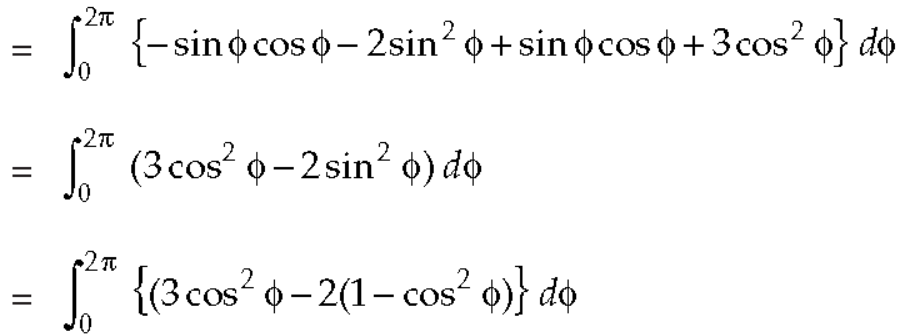

Now
Curl 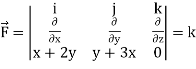
Now,
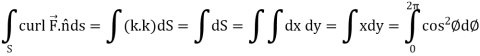

Hence the Stoke’s theorem is verified.
Gauss divergence theorem
If V is the volume bounded by a closed surface S and 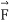 is a vector point function with continuous derivative-
is a vector point function with continuous derivative-
Then it can be written as-
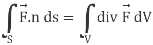
where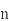 unit vector to the surface S.
unit vector to the surface S.
Example-1: Prove the following by using Gauss divergence theorem-
1. 
2. 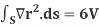
Where S is any closed surface having volume V and 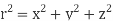
Sol. Here we have by Gauss divergence theorem-

Where V is the volume enclose by the surface S.
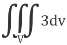
We know that-

= 3V
2.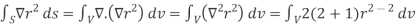
Because 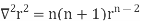
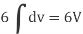
Example – 2 Show that 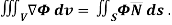
Sol
By divergence theorem, 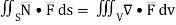 ...… (1)
...… (1)
Comparing this with the given problem
let 
Hence, by (1)
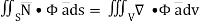 …………. (2)
…………. (2)
Now,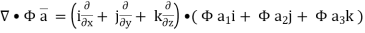

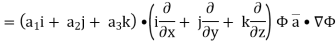
Hence, from (2), We get,

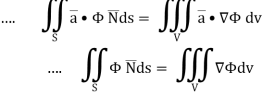
Example Based on Gauss Divergence Theorem
1. Show that
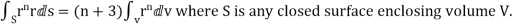
Soln. We have Gauss Divergence Theorem

By data, F=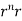

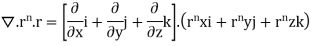
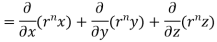
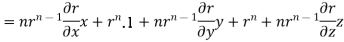
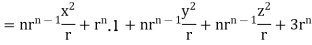
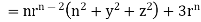
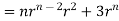
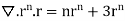
=(n+3)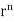


2. Prove that 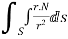 =
=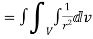
Soln. By Gauss Divergence Theorem,
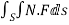 =
=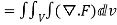
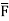 =
=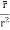 =
=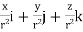
 .[
.[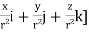
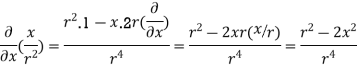
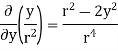
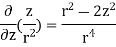
 =
= 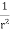
References: