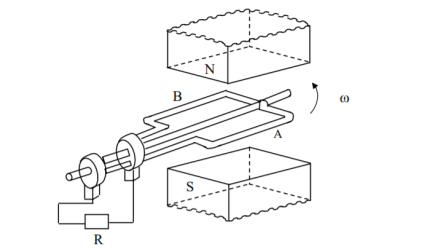
Figure 1. Schematic diagram for single phase ac generation
A multi-turn coil is placed inside a magnet with an air gap as shown in Figure. The flux lines are from North Pole to South Pole. The coil is rotated at an angular speed, ω = 2π n (rad/s).
n = w/2π = speed of the coil (rev/sec or rps)
N = 60 . n = speed of the coil (rev/min or rpm)
l = length of the coil
b = width of the diameter
T = turns of the coil
B= flux density in the air gap (Wb/m2 )
v = π . b. n (tangential velocity of the coil)
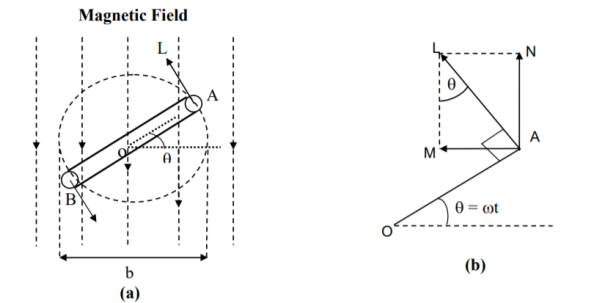
(a) Figure 2. a) Coil position b) details
At a certain instant t, the coil is an angle (rad), θ = ωt with the horizontal
The emf (V) induced on one side of the coil (conductor) is B l v sinθ , θ can also be termed as angular displacement.
The emf induced in the coil (single turn) is θ = 2B l π b n sinθ
The total emf induced or generated in the multi-turn coil is e(θ )= T2B l π b n sinθ = 2 π B l b n T sin 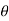 = Em sin
= Em sin 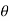
This emf as a function of time, can be expressed as, e(t) = Em sin wt . The graph of e(t) or e( ) which is a sinusoidal waveform s show in figure .
) which is a sinusoidal waveform s show in figure .
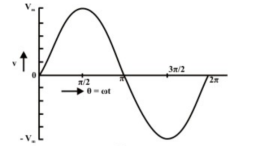
Figure 3. Time function
The area of the coil (m 2 ) = a = lb .
Flux cut by the coil (Wb) = ɸ = a . B = l . b . B
Flux linkage Ѱ= Tɸ = T B l b
It may be noted these values of flux φ and flux linkage ψ , are maximum, with the coil being at horizontal position, θ = 0 . These values change, as the coil moves from the horizontal position as shown in the figure (b).
The maximum value of the induced emf is
Emf = 2 π n B l b T = 2π n ɸ T = 2π n Ѱ= w Ѱ = Ѱ . d
Determination of frequency (f) of the emf generated is
f = w/ (2π) = n , no of poles being 2 that is having only one pole pair.
In the ac generator no of poles = p and the speed (rps) = n, then the frequency in Hz or cycles/sec is
F= no of cycles / sec = no of cycles per rev x no of rev per sec = no of pairs of poles x bno of rev per sec = (p/2) n
Or f = pN/120 = p/2. w/2π
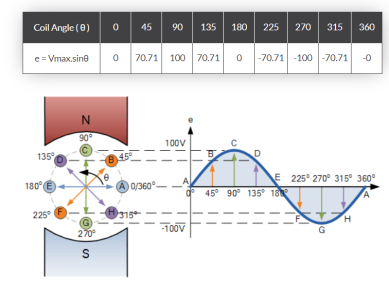
Figure 4. Sine wave
The points on the sinusoidal waveform are obtained by projecting across from the various positions of rotation between 0o and 360o to the ordinate of the waveform that corresponds to the angle, θ and when the wire loop or coil rotates one complete revolution, or 360o, one full waveform is produced.
From the plot of the sinusoidal waveform we can see that when θ is equal to 0o, 180o or 360o, the generated EMF is zero as the coil cuts the minimum amount of lines of flux. But when θ is equal to 90o and 270o the generated EMF is at its maximum value as the maximum amount of flux is cut.
Therefore, a sinusoidal waveform has a positive peak at 90o and a negative peak at 270o. Positions B, D, F and H generate a value of EMF corresponding to the formula:
e = Vmax.sinθ.
Then the waveform shape produced by our simple single loop generator is commonly referred to as a Sine Wave as it is said to be sinusoidal in its shape.
polar & rectangular
The instantaneous voltage equation is given by
Vt= vm sin (w t +Ø)
which can be represented by polar form
vt = 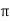 L Ø
L Ø
where 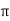 = peak value
= peak value
e.g. vt =30 sin (w t + 90 )
)
polar form 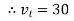 < 90
< 90
polar form is suitable for multiplication and division of phases.
2. Rectangular Form:
The instantaneous voltage equation is given by
Vt = v m sin (w t +Ø)
which can be represented by Rectangular Form
vt = 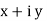
where X = 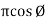 or Vm cos Ø
or Vm cos Ø
Y =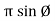 or Vm sin Ø
or Vm sin Ø
Vt = v m cos Ø + i vm sin Ø
e.g. 30 sin (w t + 90)
Rectangular form vt = 30 cos 90 + i 30 sin 90
 Rectangular Form is suitable for addition and subtraction of Phases.
Rectangular Form is suitable for addition and subtraction of Phases.
Exponential & trigonometric representations
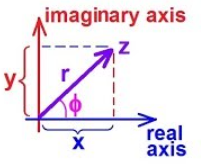
z= z e jɸ
R->P r= √ x2 + y2 ɸ = tan -1 (x/y)
P->R x=rcosɸ y=rsinɸ
Z=rejɸ
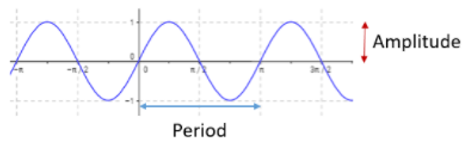
y = A sin [ B(x-C)]+D
|A| is the amplitude
Period is 2π/B
Phase shift is C and vertical shift is D.
For tangent function period is π/B
Ac circuit containing pure resisting
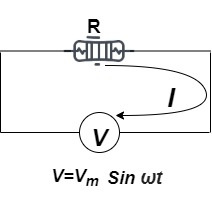
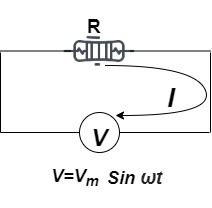
Figure 5. Resistance
Consider Circuit Consisting pure resistance connected across ac voltage source
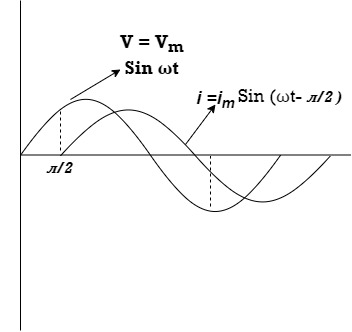
V = Vm Sin ωt ①
According to ohm’s law i =  =
= 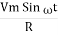
But Im = 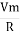
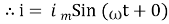 ②
②
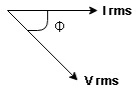
Phases diagram
From ① and ② phase or represents RMD value.
phase or represents RMD value.

Figure 6. Phasor
Power P = V. i
Equation P = Vm sin ω t Im sin ω t
P = Vm Im Sin2 ω t
P = 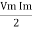 -
- 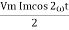
Constant fluctuating power if we integrate it becomes zero
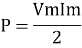
Average power
Pavg = 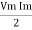
Pavg = 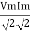
Pavg = Vrms Irms
Power ware form [Resultant]
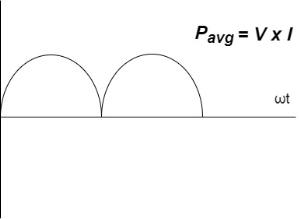
Figure 7. Power waveform
Ac circuit containing pure Inductors
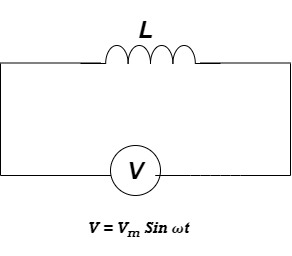
Figure 8. Inductance
Consider pure Inductor (L) is connected across alternating voltage. Source
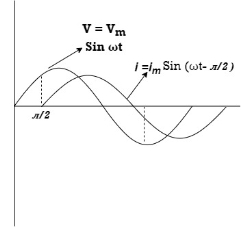
V = Vm Sin ωt
When an alternating current flow through inductance it set ups alternating magnetic flux around the inductor.
This changing the flux links the coil and self-induced emf is produced
According to faradays Law of E M I
e = 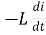
at all instant applied voltage V is equal and opposite to self-induced emf [ lenz’s law]
V = -e
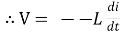 =
= 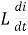
But V = Vm Sin ωt
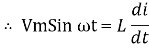
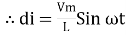 dt
dt
Taking integrating on both sides
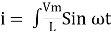 dt
dt
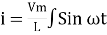 dt
dt
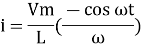
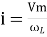 (-cos
(-cos 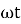 )
)
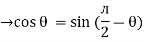
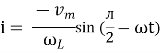
but sin (–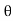 ) = sin (+
) = sin (+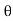 )
)
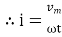 sin (
sin (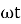 -
-  /2)
/2)
And Im= 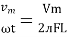
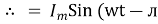 /2)
/2)
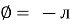 /2
/2
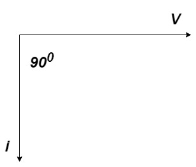
= -ve
= lagging
= I lag v by 900
Waveform:
Phasor:
Power P = Ѵ. I
= Vm sin wt Im sin (wt 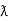 /2)
/2)
= Vm Im Sin wt Sin (wt – 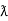 /s)
/s)
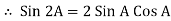 ①
①
And
Sin (wt - 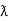 /s) = - cos wt ②
/s) = - cos wt ②
Sin (wt – 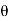 ) = - cos
) = - cos 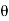
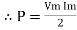 sin 2 wt from ① and ②
sin 2 wt from ① and ②
The average value of sin curve over a complete cycle is always zero
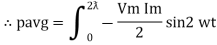
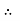 Pavg = 0
Pavg = 0
Ac circuit containing pure capacitors:
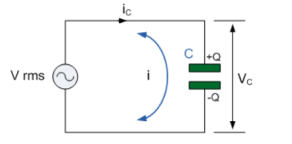
Figure 9. Capacitance
Consider pure capacitor C is connected across alternating voltage source
Ѵ = Ѵm Sin wt
Current is passing through capacitor the instantaneous charge ɡ produced on the plate of capacitor
ɡ = C Ѵ
ɡ = c Vm sin wt
the current is rate of flow of charge
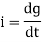
i=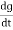 (cvm sin wt)
(cvm sin wt)
i = c Vm w cos wt
then rearranging the above eqth.
i = 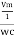 cos wt
cos wt
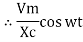
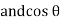 = sin (wt +
= sin (wt + 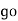 X/2)
X/2)
i = 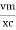 sin (wt + X/2)
sin (wt + X/2)
but 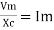
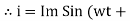 X/2)
X/2)
= leading
= I leads V by 900
Waveform :
Phase
Power P= Ѵ. i
= [Vm sinwt] [ Im sin (wt + X/2)]
= Vm Im Sin wt Sin (wt + X/2)]
 (cos wt)
(cos wt)
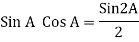
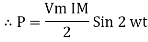
 to charging power waveform [resultant].
to charging power waveform [resultant].
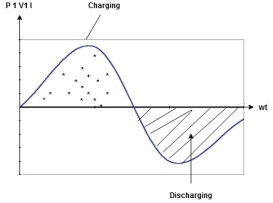
Figure 10. Power Waveform
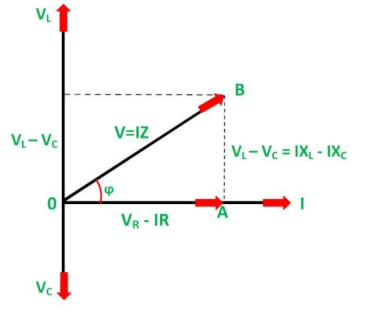
V = √ (VR) 2 + (VL-Vc) 2 = √ (IR)2 + (IXL – IXC) 2 or
V= I √ R2 + (XL -XC) 2 or
I = V / √ R2 + (XL -Xc) 2 = V/Z
Where
Z = √ R2 + (XL-XC) 2
Two impedances in parallel
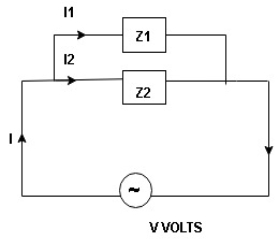
Figure 11. Impedance in parallel
I1 an I2 can be founded using current division rules
It states that the current in one branch is the products, ratio of total current and opposite branch (impedance / reactance / resistance) to the total (impedance / reactance / resistance)
 above ckt. Can be found using following steps
above ckt. Can be found using following steps
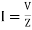
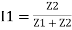
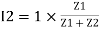 or z
or z
Admittance
Admittance is defined as reciprocal of the impedance (Z)
It is denoted by Y and its unit Siemens (S)
 Admittance Y =
Admittance Y = 
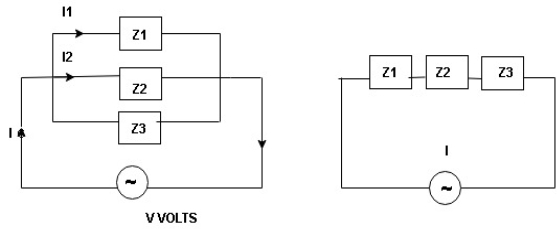
Figure 12. Admittance
I = I1 + I2 + I3
 =
= 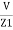 +
+ 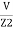 +
+ 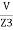
 =
= 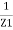 +
+ 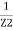 +
+ 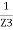
Y = Y1 + Y2 + Y3
Rationalize the expression of Y as follows
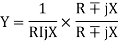
Y = 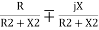
But Z2 = R2 + X2
 Y =
Y = 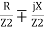
Let 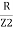 + G + conductance
+ G + conductance
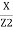 = B = susceptance
= B = susceptance
 Y = G
Y = G 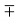 jB
jB
Conductance (G) : it is defined as the ratio of resistance R and the squared impedance (Z2) and it is measured in Siemens or mho 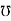
G = 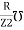
Theoretically G = reciprocal od resistance.
reciprocal od resistance.
Susceptance (B) :it is defined as the ratio of reactance X and the squared impedance (Z2) or mho 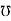
B = 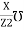
Theoretically B = reciprocal od resistance.
reciprocal od resistance.
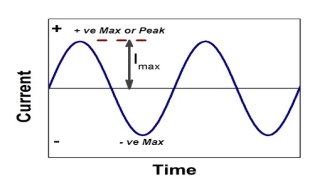
Figure 14. Peak value
Peat to peak value:
The value of an alternating quantity from its positive peak to negative peak
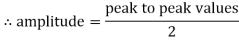
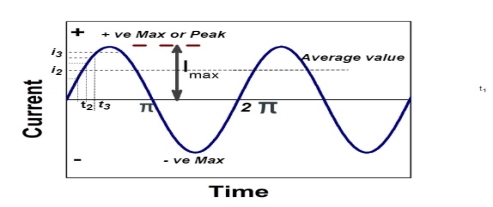
Figure 15. Average value
The arithmetic mean of all the value over complete one cycle is called as average value
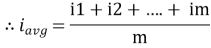
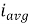 =
= 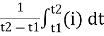
For the derivation we are considering only hall cycle.
Thus 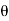 varies from 0 to ᴫ
varies from 0 to ᴫ
i = Im Sin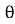
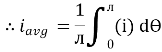
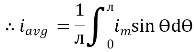
Solving
We get
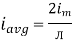
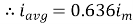
Similarly, Vavg=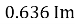
The average value of sinusoid ally varying alternating current is 0.636 times maximum value of alternating current.
RMS value: Root mean square value
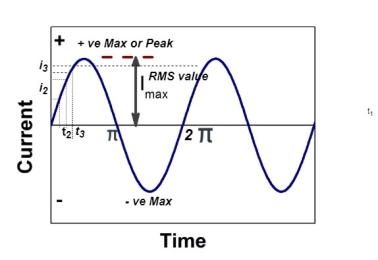
Figure 16. RMS value
The RMS value of AC current is equal to the steady state DC current that required to produce the same amount of heat produced by ac current provided that resistance and time for which these currents flows are identical.
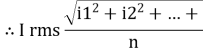
I rms = 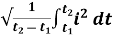
Direction for RMS value:
Instantaneous current equation is given by
i = Im Sin 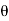
but 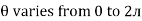
I rms = 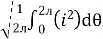
= 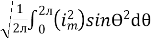
=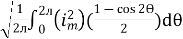
=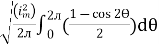
Solving
=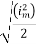
=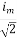
Similar we can derive
V rms= 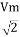 or 0.707 Vm
or 0.707 Vm
 the RMS value of sinusoidally alternating current is 0.707 times the maximum value of alternating current.
the RMS value of sinusoidally alternating current is 0.707 times the maximum value of alternating current.
Peak or krest factor (kp) (for numerical)
It is the ratio of maximum value to rms value of given alternating quantity
Kp = 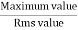
 Kp =
Kp = 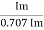
 Kp = 1.414
Kp = 1.414
Form factor (Kf): For numerical “It is the ratio of RMS value to average value of given alternating quality”.
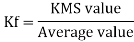
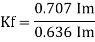
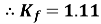
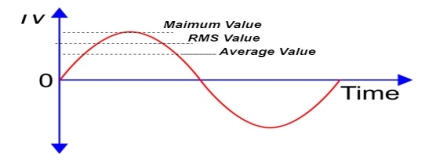
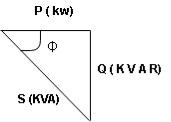
Figure 17. Maximum value
It is measured in watts
P = VI  Φ watts / KW, where Φ is the power factor angle.
Φ watts / KW, where Φ is the power factor angle.
It is defined as the product of voltage, current and sine B and I
Therefore,
Q= V.I  Φ
Φ
Unit –V A R
In kilo- KVAR
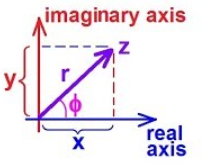
Figure 18. Reactive power
As we know power factor is cosine of angle between voltage and current
i.e. Φ.F= CosΦ
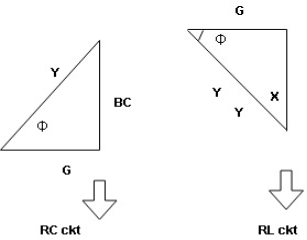
In other words also we can derive it from impedance triangle
Now consider Impedance triangle in R.L.ckt
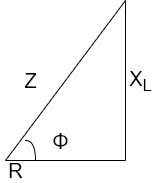
From triangle ,
Now 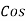 Φ – power factor=
Φ – power factor= 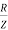
Power factor = 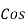 Φ or
Φ or 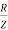
S= V × I
Unit - Volte- Ampere (VA)
In kilo – KVA
Power factor, cos(Φ), is an important part of an AC circuit that can also be expressed in terms of circuit impedance or circuit power. Power factor is defined as the ratio of real power (P) to apparent power (S), and is generally expressed as either a decimal value, for example 0.95, or as a percentage: 95%.
Complex power (in VA) is the product of the rms voltage phasor and the complex conjugate of the rms current phasor. As a complex quantity, its real part is real power P and its imaginary part is reactive power Q.
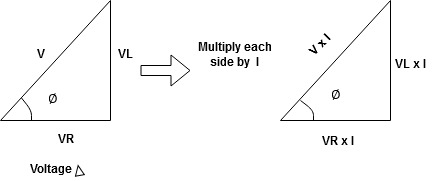
Series R-L Circuit
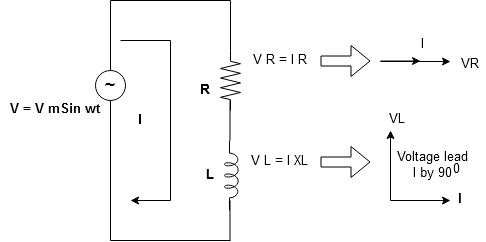
Figure 19. Series RL circuit
Consider a series R-L circuit connected across voltage source V= Vm sin wt
As some I is the current flowing through the resistor and inductor due do this current voltage drops arcos R and L R  VR = IR and L
VR = IR and L 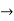 VL = I X L
VL = I X L
 Total V = VR + VL
Total V = VR + VL
V = IR + I X L  V = I [R + X L]
V = I [R + X L]
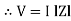
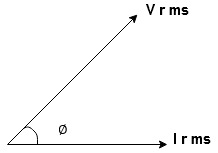
Take current as the reference phasor : 1) for resistor current is in phase with voltage 2) for Inductor voltage leads current or current lags voltage by 90 0.
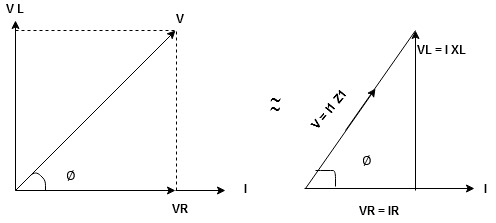
For voltage triangle
Ø is power factor angle between current and resultant voltage V and
V = 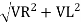
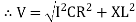
V = 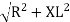
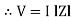
where Z = Impedance of circuit and its value is 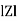 =
= 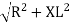
Impedance Triangle
Divide voltage triangle by I
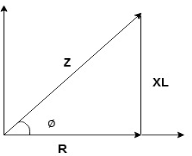
Rectangular form of Z = R+ixL
and polar from of Z = 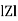 L +
L + 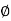
(+ j X L + 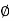 because it is in first quadrant )
because it is in first quadrant )
Where 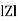 =
= 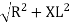
 + Tan -1
+ Tan -1 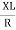
Current Equation :
From the voltage triangle we can sec. that voltage is leading current by  or current is legging resultant voltage by
or current is legging resultant voltage by 
Or i = 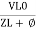 =
= 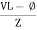 [ current angles - Ø )
[ current angles - Ø )
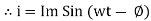
Resultant Phasor Diagram from Voltage and current eqth.
Wave form
Power equation
P = V .I.
P = Vm Sin wt Im Sin wt – Ø
P = Vm Im (Sin wt) Sin (wt – Ø)
P = 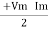 (Cos Ø) - Cos (2wt – Ø)
(Cos Ø) - Cos (2wt – Ø)
Since 2 sin A Sin B = Cos (A-B) – Cos (A+B)
P = 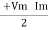 Cos Ø -
Cos Ø - 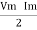 Cos (2wt – Ø)
Cos (2wt – Ø)
①②
Average Power
pang = 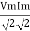 Cos Ø
Cos Ø
Since ② term become zero because Integration of cosine come from 0 to 2ƛ
 pang = Vrms Irms cos Ø watts.
pang = Vrms Irms cos Ø watts.
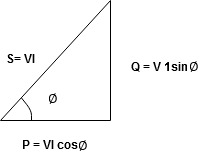
Power Triangle :
From 
VI = VRI + VLI B
Now cos Ø in 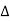 A =
A = 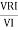
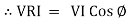 ①
①
Similarly Sin 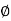 =
= 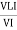

Apparent Power Average or true Reactive or useless power
Or real or active
-Unit (VI) Unit (Watts) C/W (VAR) denoted by (Ø)
Denoted by [S] denoted by [P]
Power  for R L ekt.
for R L ekt.
Series R-C circuit
V = Vm sin wt
VR

 I
I
Figure 20 . RC series circuit
R and C  voltage drops across.
voltage drops across.
R and C  R
R  VR = IR
VR = IR
And C  Vc = I
Vc = I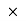 c
c
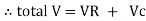
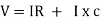
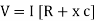
 V =
V =  lZl
lZl
Voltage triangle : take current as the reference phasor 1) for resistor current is in phase with voltage 2) for capacitor current leads voltage or voltage lags behind current by 900
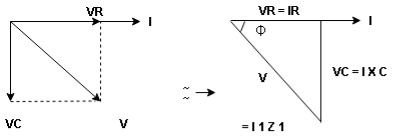
Where Ø is power factor angle between current and voltage (resultant) V
And from voltage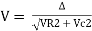
V = 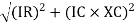
V = 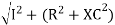
V = 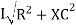
V = 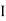 lZl
lZl
Where Z = impedance of circuit and its value is lZl = 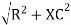
Impendence triangle :
Divide voltage  by
by  as shown
as shown
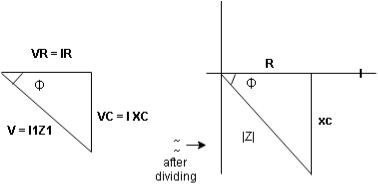
Rectangular from of Z = R - jXc
Polar from of Z = lZl L - Ø
( - Ø and –jXc because it is in fourth quadrant ) where
lZl = 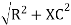
and Ø = tan -1 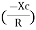
Current equation :
from voltage triangle we can see that voltage is lagging current by Ø or current is leading voltage by Ø
 i = IM Sin (wt + Ø) since Ø is +ve
i = IM Sin (wt + Ø) since Ø is +ve
Or i = 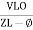 for RC
for RC
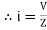 LØ [ resultant current angle is + Ø]
LØ [ resultant current angle is + Ø]
Resultant phasor diagram from voltage and current equation
Resultant wave form :
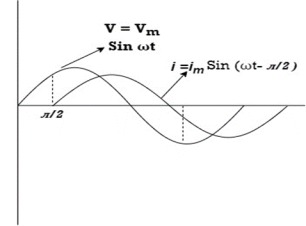
Power Equation :
P = V. I
P = Vm sin wt. Im Sin (wt + Ø)
= Vm Im sin wt sin (wt + Ø)
2 Sin A Sin B = Cos (A-B) – Cos (A+B)
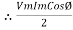 -
- 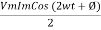
Average power
pang =  Cos Ø
Cos Ø
since 2 terms integration of cosine wave from 0 to 2ƛ become zero
 2 terms become zero
2 terms become zero
 pang = Vrms Irms Cos Ø
pang = Vrms Irms Cos Ø
Power triangle RC Circuit:
Parallel R-L circuit
In RL parallel circuit resistor and inductor are connected in parallel with each other and this combination is supplied by voltage source Vin. The output voltage of circuit is Vout. Since the resistor and inductor are connected in parallel, the input voltage is equal to output voltage but the currents flowing in resistor and inductor are different.
The parallel RL circuit is not used as filter for voltages because in this circuit, the output voltage is equal to input voltage and for this reason it is not commonly used as compared to series RL circuit.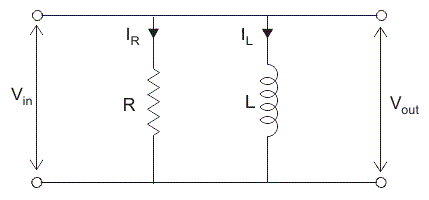
Figure 21. Parallel RL circuit
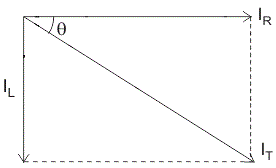
Let us say: IT = the total current flowing from voltage source in amperes.
IR = the current flowing in the resistor branch in amperes.
IL = the current flowing in the inductor branch in amperes.
θ = angle between IR and IT.
So the total current IT,
I2T = I2R + I2L
In complex form the currents are written as,
IR = Vin /R
IL = Vin / jwL
IL = -j Vin/wL (where 1/j =-j)
Therefore, total current IT = Vin/ R-j/Vin/wL
Impedance of Parallel RL Circuit
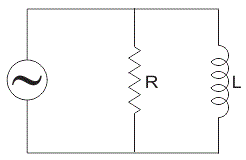
Figure 22. Impedance
Let, Z = total impedance of the circuit in ohms.
R = resistance of circuit in ohms.
L = inductor of circuit in Henry.
XL = inductive reactance in ohms.
Since resistance and inductor are connected in parallel, the total impedance of the circuit is given by,
1/Z = 1/R + 1/jXL
Z = R * (jXL)/ R +jXL
In order to remove “j” from the denominator multiply and divide numerator and denominator by (R – j XL),
Z = R * (jXL) / R+jXL) * R-jXL/ R-jXL
= j R2 XL – j2 R2 XL2 / R2 + XL2
Since j2 = -1
RXL2 + j R2 XL / R2 + XL2
Z = RXL2 / R2 + XL2 + j R2 XL / R2 + XL2
Parallel RC circuit
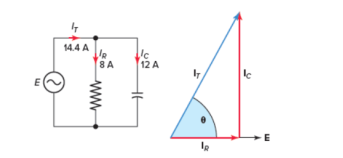
Figure 12. Parallel RC circuit
In a parallel RC circuit, the line current leads the applied voltage by some phase angle less than 90 degrees but greater than 0 degrees. The exact angle depends on whether the capacitive current or resistive current is greater. If there is more capacitive current, the angle will be closer to 90 degrees, while if the resistive current is greater, the angle is closer to 0 degrees.
The value of the phase angle can be calculated from the values of the two branch currents using the following equation:
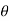 = tan-1 Ic/IR
= tan-1 Ic/IR
Current in Parallel RC Circuit
For the parallel RC circuit shown in Figure 3, determine:
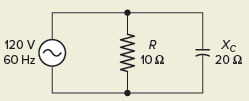
Figure Circuit .
Solution:
a. IR=ER=120V10 Ω =12Aa. IR=ER=120V10 Ω =12A
b. IC=EXC=120V20 Ω =6Ab. IC=EXC=120V20 Ω =6A
c. IT=√I2R+I2C=√122+62=13.4Ac. IT=IR2+IC2=122+62=13.4A
d.θ=tan−1(ICIR)=tan−1(612)=26.6od.θ=tan−1(ICIR)=tan−1(612)=26.6o
e. IT=13.4∠26.6ooIR=12∠0oIC=6∠90oe. IT=13.4∠26.6ooIR=12∠0oIC=6∠90o
f. IT=12+j6IR=12+j0IC=0+j6f. IT=12+j6IR=12+j0IC=0+j6
Parallel RC Circuit Impedance
The impedance (Z) of a parallel RC circuit is similar to that of a parallel RL circuit and is summarized as follows:
Z = RXC / √ R2 + X 2 C
AC serial circuit:
R-L-C series circuit
Figure 13. Series RLC circuit
Consider ac voltage source V = Vm sin wt connected across combination of R L and C. when I flowing in the circuit voltage drops across each component as shown below.
VR = IR, VL = I  L, VC = I
L, VC = I  C
C
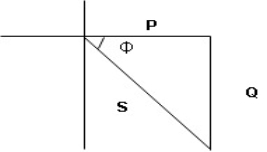
① XL> XC, ② XC> XL, ③ XL = XC
① XL > XC: Since we have assumed XL> XC
 Voltage drop across XL> than XC
Voltage drop across XL> than XC
 VL> VC A
VL> VC A
VL and VC are 180 0 out of phase .
Therefore cancel out each other
 Resultant voltage triangle
Resultant voltage triangle
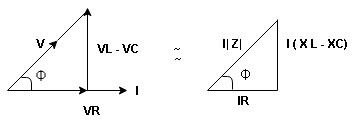
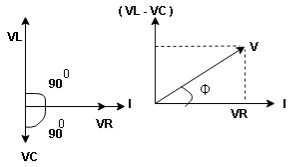
Now V = VR + VL + VC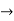 c phasor sum and VL and VC are directly in phase opposition and VL
c phasor sum and VL and VC are directly in phase opposition and VL VC
VC their resultant is (VL - VC).
their resultant is (VL - VC).
From voltage triangle
V = 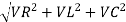
 V =
V = 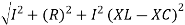
 V = I
V = I 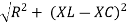
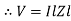
Impendence 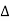 : divide voltage
: divide voltage 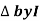
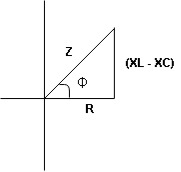
Rectangular form Z = R + j (XL – XC)
Polor form Z = 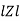 l + Ø B
l + Ø B
Where 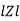 =
= 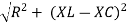
And Ø = tan-1 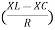
i = 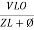 from B
from B
i =  L-Ø C
L-Ø C
as VL VC the circuit is mostly inductive and
VC the circuit is mostly inductive and  I lags behind V by angle Ø
I lags behind V by angle Ø
 Since i =
Since i =  L-Ø
L-Ø
 i = Im Sin (wt – Ø) from c
i = Im Sin (wt – Ø) from c
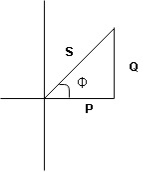


 the voltage drops across XC
the voltage drops across XC  than XL
than XL
 XC
XC  XL (A)
XL (A)
 voltage triangle considering condition (A)
voltage triangle considering condition (A)
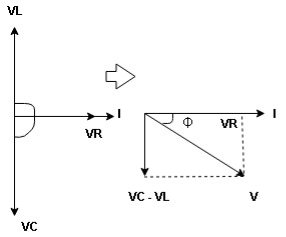
 Resultant Voltage
Resultant Voltage 
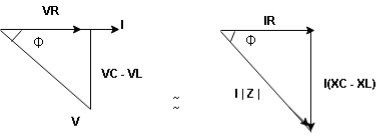
Now V = VR + VL + VC  phases sum and VL and VC are directly in phase opposition and VC
phases sum and VL and VC are directly in phase opposition and VC VL
VL  their resultant is (VC – VL)
their resultant is (VC – VL)
From voltage 
V = 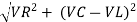
V = 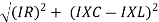
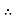 V =
V = 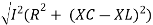
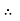 V =
V = 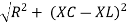
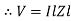
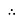 Impedance
Impedance 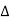 : Divide voltage
: Divide voltage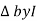
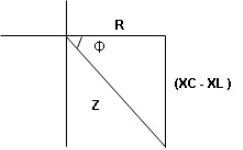
Polar form : Z = 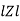 L -
L -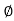
Where 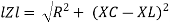
And Ø = tan-1 – 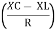
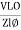

as VC 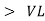 the circuit is mostly capacitive and
the circuit is mostly capacitive and 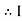 leads voltage by angle Ø
leads voltage by angle Ø
since i = 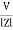 L + Ø
L + Ø
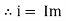 Sin (wt – Ø) from C
Sin (wt – Ø) from C
ɡȴ XL= XC then VL= VC and they are 1800 out of phase with each other  they will cancel out each other and their resultant will have zero value.
they will cancel out each other and their resultant will have zero value.
Hence resultant V = VR and it will be in phase with I as shown in below phasor diagram.
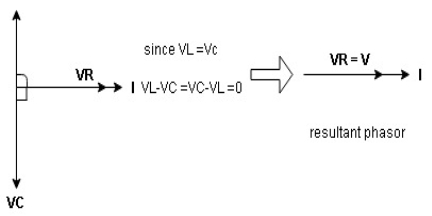
From above resultant phasor diagram
V =VR + IR
Or V = I  lZl
lZl
Because lZl + R
Thus Impedance Z is purely resistive for XL = XC and circuit current will be in phase with source voltage.

 Since VR=V Øis zero when XL = XC
Since VR=V Øis zero when XL = XC  power is unity
power is unity
ie pang = Vrms I rms cos Ø = 1 cos o = 1
maximum power will be transferred by condition. XL = XC
AC parallel circuit:
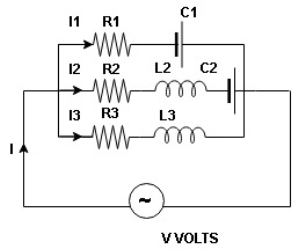
Figure 14. Parallel RLC circuit
Total I = I1 + I2 + I3
As parallel circuit  applied total voltahe V is same at each branch
applied total voltahe V is same at each branch
I = I1 + I2 + I3
=  =
= 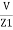 +
+ 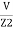 +
+ 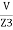
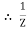 =
= 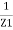 +
+ 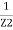 +
+ 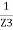 +……
+……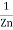
Resonance in series RLC circuit
Definition:
It is defined as the phenomenon which takes place in the series or parallel R-L-C circuit which leads to unity power factor
Voltage and current in R-L-C ckt are in phase with each other.
Resonance is used in many communication circuits such as radio receiver.
Resonance in series RLC -> series resonance in parallel->antiresonance/parallel resonance
Condition for resonance
XL=XC
Resonant frequency (fr): For given values R-L-C the inductive reactance XL becomes exactly equal to the capacitive reactance XC only at one particular frequency. This frequency is called as resonant frequency and denoted by ( fr)
Expression for resonant frequency (fr)
We know that
XL = 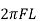 - inductive reactance
- inductive reactance
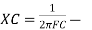 capacitive reactance
capacitive reactance
At a particle or frequency f=fr,the inductive and capacitive reactance are exactly equal
Therefore, XL = XC ----at f=fr
i.e. 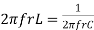
Therefore, 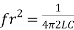
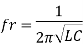
and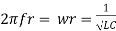 rad/sec
rad/sec
Resonance in parallel RLC circuit
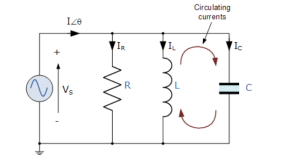
Figure 15. Parallel resonance
A parallel resonant circuit stores the circuit energy in the magnetic field of the inductor and the electric field of the capacitor. This energy is constantly being transferred back and forth between the inductor and the capacitor which results in zero current and energy being drawn from the supply.
Admittance Y = 1/Z = √ G2 + B2
Conductance G = 1/R
Inductive susceptance BL = 1/ 2π f L
Capacitive susceptance Bc = 2π f C
The quality of resonance circuit is measured in terms of efficiency of L and C to stare energy and the efficiency of L and C to store energy as measured in terms of a factor called quality factor or Q factor it is expressed as
Q = 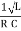 and Q =
and Q = 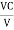
The sharpness of tuning of R-L-C series circuit or its selectivity is measured by value of Q. as the value of Q increases, sharpness of the curve also increases and the selectivity increases.
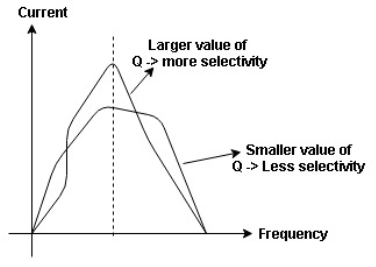
Figure 16. Quality factor
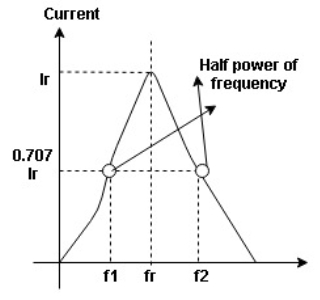
Figure 17. Bandwidth
Bandwidth (BW) = f2 = b1
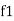 and
and 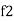 are the frequency at which the power delivered to the resistor is reduced to 50% of the power delivered to it at resonance
are the frequency at which the power delivered to the resistor is reduced to 50% of the power delivered to it at resonance  these frequencies are called as half power frequency
these frequencies are called as half power frequency
Bw = fr/Q
Frequency points ƒL and ƒH relate to the lower corner or cut-off frequency and the upper corner or cut-off frequency points respectively were the circuits gain falls off at high and low frequencies. These points on a frequency response curve are known commonly as the -3dB (decibel) points. So the bandwidth is simply given as:
Bandwidth = fH -fL.
References:
o Basic Electrical Engineering Book by I.J. Nagrath
o Objective Electrical Technology Book by Rohit Mehta and V.K. Mehta