UNIT 1

RATIO

1.1 Ratio - Gaining and sacrificing ratio, proportion, percentage, commission, discount and brokerage.

Ratio-

The ratio of two quantities ‘x’ and ‘y’ of same kind is obtained by dividing x by y and it is denoted by x : y

The first term is called antecedent and the second term is called consequent.

Example: 2/3 or 2:3

Example: Divide 500 into two people A and B ratio 2:3.

Sol.

Here sum of the ratio is  = 2 + 3 = 5

Then,

A’s share =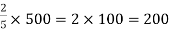

B’s share =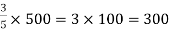

Continued ratio-

A ratio is said to be in continued if consequent of one ratio is antecedent of the other.

For example- a:b and b:c is in continued ratio.

Example: If Rs. 74000 are to be divided among three people X, Y and Z such that X : Y = 4 : 5 and Y : Z = 3 : 2 then what amount each person will recieve?

Sol.

Here X:Y:Z: =   12:15:10

Here sum of the ratio is = 12 + 15 + 10 = 37

Then-

X will get =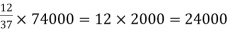

Y will get =

Z will get =

Inverse ratio-

For the ratio x : y, the inverted ratio will be y:x.

Example: inverse ratio of 3:4 is 4:3

Note-

A ratio remains same if it is multiplied or divided by the same number.

X: y = mx : my ( multiplied by ‘m’)

X:y = x/m:y/m (divided by m)

Example:

4:5 =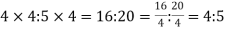

Gaining Ratio and Sacrificing Ratio

Sacrificing Ratio is the ratio in which old partners sacrifice their share in profits in favour of new or incoming partners, Whereas, gaining ratio is the ratio in which remaining partners acquire the outgoing partner's share.

Therefore, the Sacrifice ratio arises when the old profit share of the existing partners is more than the new profit share in the newly reconstituted firm. Thus, it can be computed by deducting the new ratio from the old ratio (i.e., Sacrifice ratio = Old ratio –New Ratio). 

1. A and B are partners sharing profits in the ratio of 3:2. A new partner, C is admitted for a one-sixth share in the future profit. The new profits sharing ratio among A, B and C and Sacrifice ratio of A and B shall be computed as under:

Solution:

Computation of New profit ratio and Sacrifice ratio: –

Old ratio among A and B is 3:2

Share of New partner, C is 1/6

Remaining future share for A and B = 1 – 1/6 = 5/6

(This needs to be shared among A and B in 3:2)

Thus,

A’s new share = 5 /6 × 3/5 = 3/6

B’s new share = 5 /6 × 2/5 = 2/6

And C’s share is already given as 1/6

Hence, New Profit ratio among A:B:C is 3:2:1

Here, the Sacrifice ratio among A and B is 3:2

(as they sacrifice in old ratio for share of new Partner)

2.      A and B are partners sharing profits in the ratio of 5:3. C is admitting into partnership and for this purpose, A is surrendering two eighths from his share and B surrendered one eighth from his share in favor of C. In such cases, the new sharing ratio among A, B and C and Sacrifice ratio among A and B shall be computed as under:

Solution:

Computation of New profit ratio and Sacrifice ratio

Old ratio among A and B is 5:3

New share of each partner is as under:

A’s new share = 5/8 – 2/8 = 3/8

B’s new share = 3/8 – 1/8 = 2/8

C’s new share = 2/8+1/8 = 3/8

Thus, new profit ratio among A:B:C is 3:2:3

The Sacrifice ratio among A and B is as under:

A surrendered = 2/8

B surrendered = 1 /8

Hence, Sacrifice ratio is 2:1

3.      A and B are partner sharing profits in the ratio of 3:2. A new partner has been admitted to the partnership. A surrendered one-third of his share and B surrendered one half of his share in favor of C. In such instances, the new profit-sharing ratio among A, B and C and Sacrifice ratio among A and B is computed as under:

Solution:

Computation of New profit ratio and Sacrifice ratio

Old ratio among A and B is 3:2

Sacrifice ratio among A and B is computed as under:

A surrendered = 3/5 × 1/3 = 1/5

B surrendered = 2/5 × 1/2 = 1/5

Here, Sacrifice ratio among A and B is 1:1

Now, New profit-sharing ratio is computed as under:

A’s new share = 3/5 – 1/5 = 2/5

B’s new share = 2/5 – 1/5 = 1/5

C’s share = 1/5 + 1/5 = 2/5

Hence, New ratio among A:B:C is 2:1:2

Gaining Ratio

Gaining ratio is calculated at the time of retirement or death of a partner. It is the ratio in which the remaining partners acquire the outgoing partner’s share of profit.

When the partner retires, the profit-sharing ratio of the continuing partners gets changed. Continuing partners distribute the share of retiring partner among them.

Gaining ratio= New Ratio – Old Ratio (if positive)

1. Amit, Sumit, and Punit share profit and losses in the ratio of 3:2:1, respectively. Amit retires and the remaining partners decide to share to take Amit’s share in the existing ratio i.e., 2:1. Calculate the new ratio and gaining ratio.

Solution:

The existing ratio between Sumit and Punit= 2/6 and 1/6

Amit’s ratio (retiring partner) = 3/6

Amit’s share taken by Sumit and Punit in the ratio of 2:1

Sumit gets = 3/6 * 2/3 = 6/18

Punit gets = 3/6 * 1/3 = 3/18

New ratio between Sumit and Punit is = 6:3 = 2:1

Gaining ratio= New Ratio – Old Ratio

Sumit’s gain = 2/3 – 2/6 = 2/6

Punit’s gain = 1/3 – 1/6 = 1/6

Gaining ratio = 2:1

New Ratio = 2:1

2.     Amit, Sumit, and Punit share profit and losses in the ratio of 2:3:1, respectively. Amit retires and the remaining partners decide to share to take Amit’s share equally. Calculate the new ratio and gaining ratio.

Solution:

The existing ratio between Sumit and Punit= 3/6 and 1/6

Amit’s ratio (retiring partner) = 2/6

Amit’s share taken by Sumit and Punit in the ratio of 1:1

Sumit gets = 2/6 * 1/2 = 1/6

Sumit’s new share = 3/6 + 1/6 = 4/6

Punit gets = 2/6 * 1/2 = 1/6

Punit’s new share = 1/6 + 1/6 = 2/6

New ratio between Sumit and Punit is = 4:2 = 2:1

Gaining ratio is given the question i.e., 1:1

Gaining ratio = 1:1

New Ratio = 2:1

3.     Amit, Sumit, and Punit share profit and losses in the ratio of 4:5:2, respectively. Amit retires and Punit acquires Amit’s share. Calculate the new ratio and gaining ratio.

Solution:

Punit’s new share = 2/11 + 4/11 = 6/11

Sumit share remains unchanged = 5/11

The new ratio between Sumit and Punit is = 5:6

Gaining ratio in this case between Sumit and Punit will be

Sumit’s gain = 5/11 – 5/11 = Nil

Punit’s gain = 6/11 – 2/11 = 4/11

This shows that entire gain is taken by Punit.

Proportion-

Proportion is an equation that equates two ratios in same proportion,

If the ratio a/b is equals to the ratio c/d then the following proportion can be written-

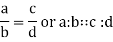
Here a and d are called the extremes of the proportion, the numbers b and c are called means of the proportion

Properties of proportion-

1. Cross product property: The product of the extremes equals the product of the means.

If then ad = bc

2.     Reciprocal property: If two ratios are equal, then their reciprocals are also equal.

If 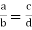then If .

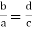Continued proportion-

The quantities p, q, r, s, t..... Are said to be in continued proportion of p:q = q:r = r:s.....

Example: If 2, x and 32 are in continued proportion then find the value of x.

Sol.

Here it can be written as-

2 : x = x:32

Or

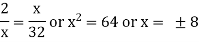
Note- if a, b, c are in continued proportion then

Fourth, third and mean proportional-

If p:q = r:s then-

1. S is called the fourth proportional to p,q,r.
2. R is called the third proportion to p and q.
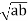3. is called the mean proportional between a and b.

Compound proportion-

If two or more ratios are multiplied together then they are known as compounded.

Thus a1 a2 a3 : b1 b2 b3 is a compounded ratios of the ratios a1 : b1 ; a2 : b2 and a3 : b3. This method is also known as compound rule of three.

Example: 10 men working 8 hours a day can finish a work in 12 days. In how many days can 12 men working 5 hours a day finish the same work?

Sol.

This can be arranged as-

Then

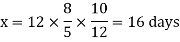
Important properties of proportion-

Given quantities a, b, c, d are in proportion.

1. Invertendo: If a : b = c : d then b : a = d : c
2. Alternendo : If a : b = c : d, then a : c = b : d
3. Componendo and Dividendo- if

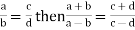
Note-

1. If x : y = a : b, it does not mean x = a, y = b. It is however to take x = ka, y = kb
2. If is sometimes written as x : y : z = a : b : c.

Example: The marks obtained by four examinees are as follows: A : B = 2 : 3, B : C = 4 : 5, C : D = 7 : 9, find the continued ratio.

Sol.

A : B = 2 : 3

B : C = 4 : 5 =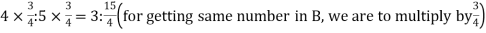

C : D = 7 : 9 =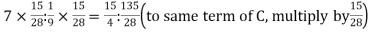

A : B : C : D = 2 : 3 :

Example: Two numbers are in the ratio of 3 : 5 and if 10 be subtracted from each of them, the remainders are in the ratio of 1 : 5, find the numbers.

Sol.

Let the numbers be x and y, so that- x/y =3/5  or 5x = 3y … (1)

Again-

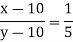
Or

5x – y = 40… (2)

By solving (1) and(2), we get-

X = 12 and  y = 20

Hence the required numbers are- 12 and 20

Example: The prime cost of an article was three times the value of material used. The cost of raw materials was increased in the ratio 3 : 4 and the productive wage was increased in the ratio 4 : 5. Find the present prime cost of an article, which could formerly be made for Rs.180.

Sol.

Prime cost = x + y, where x = productive wage, y = material used

Now prime cost = 180 =3y or, y = 60, again x + y = 180, x = 180–y = 180–60 = 120

Present material cost = 4y/3 and present wage = 5x / 4

Present prime cost–

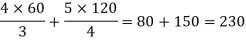
Hence the present prime cost is Rs. 230.

Direct and inverse proportion-

Direct proportion or direct variation-

Direct proportion or direct variation is the relation between two quantities where the ratio of the two is equal to a constant value. It is represented by the proportional symbol, ∝

Or we can say that two values said to be in direct proportion when one variable increases then other value also increases.

If we have two quantities ‘a’ and ‘b’ which are lined with each other directly then we can say- a ∝ b

When we remove proportionality sign, the ratio of ‘a’ and ‘b’ becomes equals to a constant.

a = Cb

For example: if the number of individuals visiting a restaurant increases, earning of the restaurant also increases.

Inverse proportion-

Inverse proportion is when one value increases and the other value decreases.

For example- We need more manpower to reduce the time to complete a task. They are inversely proportional.

Questions based on direct and inverse proportion-

Example:  A machine in a drinking water supplying factory fills 840 bottles in six hours. How many bottles will it fill in five hours?

Sol.

Let the bottles filled by machine in 5 hours be x

We can write the given information as follows-

There is a direct relationship between time taken and bottles filled by machine,

So that, we get-

So that 700 bottles can be filled by the machine in 5 hrs.

Example: In a model of a ship, the mast is 9 m high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship?

Sol.

Suppose the mast of the model ship be x, then

We can write the given information as follows-

There is a direct relationship-

So that,

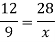
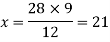
So that the length of a model ship is 21m.

Example: 10 men can do a piece of work in 30 days then in how many days 20 men can do the same work?

Sol.

Let ‘x’ days be taken to do the task,

Then

There is inverse relationship, so that-

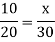
So that 20 men can do the same piece of work in 15 days.

Key takeaways-

1. The ratio of two quantities ‘x’ and ‘y’ of same kind is obtained by dividing x by y and it is denoted by x:y
2. The first term is called antecedent and the second term is called consequent.
3. A ratio is said to be in continued if consequent of one ratio is antecedent of the other.
4. For the ratio x:y, the inverted ratio will be y:x.
5. A ratio remains same if it is multiplied or divided by the same number.
6. Proportion is an equation that equates two ratios in same proportion
7. 
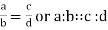
8. If 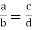then ad = bc
9. If 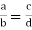then If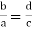
10. If two or more ratios are multiplied together then they are known as compounded.
11. When we remove proportionality sign, the ratio of ‘a’ and ‘b’ becomes equals to a constant.

a = Cb

12. Inverse proportion is when one value increases and the other value decreases.

Percentage- Meaning and computation of percentage

Percent means a part per 100. A percentage is a number that can be expressed as fraction of 100.

We use the symbol % for percentage.

We can represent percentage in decimal or fraction form.

We use the following formula to calculate percentage-

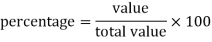
For example: if a student got 300 marks out of 500 then his result in percentage will be-

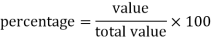
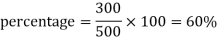
Percentage Increase and Decrease

The percentage increase is equal to the subtraction of original number from a new number, divided by the original number and multiplied by 100.

% increase = [(New number – Original number)/Original number] x 100

Where, increase in number = New number – original number

% decrease = [(Original number – New number)/Original number] x 100

Where decrease in number = Original number – New number

Example: Find 70 % of 30

Sol.

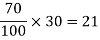
Example: A person has a monthly salary of Rs. 20,000. He spends 8000 per month on food then what percent of his monthly salary does he save?

Sol.

Person’s monthly salary = 20,000

Savings = (20,000 – 8000) = 12,000

Fraction of his saving = 12,000/20,000

By converting the fraction into percentage, we get-

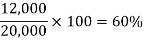
Example: A shopkeeper reduced the price of an item by 25%, the old price was 120 then find out the new price.

Sol.

25% of 120 will be-

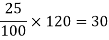
Which means he reduced Rs. 30, then the new price is-

120 – 30 = 90

The new price is Rs. 90

Example:  If 20% of any number is 500 then find out the number?

Sol.

Let the number is ‘x’, then-

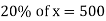
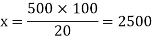
Hence the number is 2500.

Decrease in number = Original number – New number

Key takeaways-

1. 
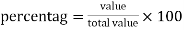
2. % increase = [(New number – Original number)/Original number] x 100
3. % decrease = [(Original number – New number)/Original number] x 100
4. Decrease in number = Original number – New number

Introduction to commission and brokerage- problems on commission and brokerage

The amount received by the agency for providing its services is known as ‘brokerage’ or ‘commission’.

For example- placement agencies, marriage bureaus etc.

An individual can also run this type of business

Note- An individual who acts as a ‘middle man’ between a seller and buyer is known as broker.

Brokerage is paid by purchaser, Commission is paid by seller. Therefore

Net amount paid by purchaser = Sale price + brokerage

Net amount received by seller = Sale price - commission

Commission % = Commission100 /Selling price

Selling Price = Commission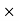100/ Commission %

Commission (Brokerage) = Commission%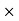Selling price/100

Example: The Price of a book is Rs. 15.75. A book seller sells 1200 books and pays Rs 17,860.50 to the book publisher after deducting his commission.  

Find the commission rate.

Sol.

Here we have total commission,

We have to find the total sale price of books.

The total sale price of books = Number of Books Price = 1200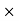15.75 =18900

Commission = Sale price – Amount paid to the Publisher = 18900-17860.5 = 1039.5

Commission % = Commission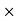100 /Selling price = 1039.5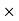100/18900 = 5.5%

Example: Mahesh sold his car for Rs.68,000 with the help of an agent. If the commission paid by Mahesh is Rs 2550. Find rate of commission, and the net amount received  by the Mahesh.

Sol.

Commission % = Commission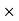100 /Selling price = 2550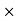100/68000 = 3.75%

Net amount received by farmer = Sale price – Commission = 68000-2550 = Rs65, 450

Example: An agency pays 15% commission to a notebook distributor. The price of each notebook is Rs 3. If he sells 50 copies of notebook every day, find how much commission he receives in a month and also net amount received by the Agency?

Sol.

Price of each news paper = Rs 3.

Sale price for a day = Number copies sold in day price of Cost of news paper = 50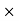3 = Rs 150

Sale price for a year = Number of daysSale price for a day = 30150 = 450 Rs

Commission = Commission%Selling price/100 = 15450/100 = 67.5 Rs.

Net amount received by agency = selling price – commission = 450 -67.5 = 382.5 Rs

Key takeaways-

1. Net amount paid by purchaser = Sale price + brokerage

Net amount received by seller = Sale price - commission

2.     Commission % = Commission100 /Selling price

3.     Selling Price = Commission100/ Commission %

4.     Commission (Brokerage) = Commission%Selling price/100

Discount

Cost Price (CP) - The price at which an article is purchased.

Selling Price (SP) - This is the price at which an article is sold.

Profit - If the selling price is more than the cost price, then there will be profit

Profit = Selling price (SP) – Cost price (CP)

Profit % = (profit100)/CP

Loss - If the selling price is less than the cost price, then there will be loss

Loss = Cost price (CP) – Selling price (SP)

Loss% = (Loss 100)/CP

Marked Price - This is the price marked as the selling price on an article, also known as the listed price

Note- Profit or Loss is always calculated on the cost price.

Discount: This is the reduction in price offered on the marked or listed price.

Example: Suppose the profit percentage is 80% of the cost. If the cost further increases by 20% but the selling price remains the same, how much is the decrease in profit percentage?

Sol.

Let us suppose

CP = Rs. 100.

Then Profit = Rs. 80 and selling price = Rs. 180.

The cost increases by 20% → New CP = Rs. 120, SP = Rs. 180.

Profit % = 60/120 100 = 50%.

Therefore, Profit decreases by 30%.

Example: A dishonest shopkeeper sells his grocery using weights 15% less than the true weights and makes a profit of 20%. Find his total gain percentage.

Sol.

Suppose 1 kg of grocery bag.

Its actual weight is 85% of 1000 gm = 850 gm.

Let the cost price of each gram be Re. 1. Then the CP of each bag = Rs. 850.

SP of 1 kg of bag = 120% of the true CP

Therefore, SP = 120/100 1000 = Rs. 1200

Gain = 1200 – 850 = 350

Hence Gain % = 350/850 100 = 41.17%

Example: A shopkeeper offers a discount of 20% on the selling price. On a special sale day, he offers an extra 25% off coupon after the first discount. If the article was sold for Rs. 3600, find the marked price of the article

Sol.

Let the marked price of the article be x.

First a 20% discount was offered, on which another 25% discount was offered.

So, 75% of 80% of x = 3600

75/100 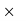80/100 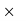x = 3600 → x = 6000.

So the article was marked at Rs. 6000.

Example: The cost price of 30 articles is equal to the selling price of 40 articles. What is the profit or loss percentage?

Sol.

CP of 30 articles = SP of 40 articles Or, CP/SP = 30/40 =3/4

Or, 1 – CP/SP = 1- 3/4 = 1/4

So, Loss percentage

= (l – CP/SP) x 100 = 1/4x 100 = 25%

Trade discount-

Trade discount is a certain percentage a manufacturer is willing to reduce its list price for wholesalers or retailers.

Trade discounts are given to wholesalers that order large quantities of a product as well as retailers with good relationships with the manufacturer. Purchase discounts or Cash discount are based on payment plans not order quantities.

Trade discounts are offered on bulk purchases by traders, wholesalers, distributors or retailers and not to the end consumers.

Trade discounts are generally offered at varied rates depending on the volume of sale

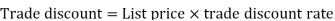
And

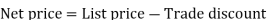
Example: Sweety purchases a set of toys that lists for Rs. 950 and it has a trade discount of 30%, then find the net price.

Sol.

As we know that-

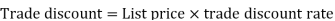
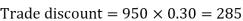
Then

Net price = 950 – 285 = 665

Example: If Raheem will buy a table that lists for Rs. 2000 and it has a trade discount of 50%. Then how much will he pay?

Sol.

As we know that-

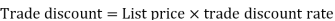
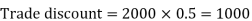
Then

Net price = 2000 – 1000 = 1000

Cash discountis allowed to stimulate instant payment of the goods purchased. 

Cash Discount is referred to as a discount, allowed to customers by the seller at the time of making the payment of purchases, as a reduction in the invoice price of the commodity.

Both the buyers and sellers keep a proper record of such discount in their books of accounts.

Sellers offer cash discounts to their buyers as an incentive to encourage early payment.

Ordinary dating method-

A credit term of [2/10, n/30] means that you will get a discount of 2% if you clear your account within 10 days

Example: A person received an invoice for Rs. 3,000 dated 22 November 2019 with terms [2/10, n/30]. He paid the whole amount on 30 November 2019. How much did he effectively paid for the bill?

Sol.

1. Date of Invoice: 22nd November 2019
2. Day 1 of the cash discount period.  : 23rd November 2019
3. Last day of the Cash discount period: 31st November 2019
4. Date of payment: 30th November 2019

Cash discount.= Price Discount rate

= Rs. 3,000 2/100

= Rs. 60

Amount effectively paid by the person = Bill value - Cash discount

= 3,000 - 60

= Rs. 2,940

Key takeaways-

1. Cost Price (CP) - The price at which an article is purchased
2. Selling Price (SP) - This is the price at which an article is sold
3. Profit = Selling price (SP) – Cost price (CP)
4. Profit = Selling price (SP) – Cost price (CP)
5. Loss = Cost price (CP) – Selling price (SP)
6. Loss% = (Loss 100)/CP
7. Marked Price - This is the price marked as the selling price on an article, also known as the listed price
8. Discount: This is the reduction in price offered on the marked or listed price.
9. Trade discount is a certain percentage a manufacturer is willing to reduce its list price for wholesalers or retailers.
10. Trade discounts are generally offered at varied rates depending on the volume of sale
11. 
12. 
13. 
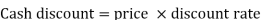
14. Gaining Ratio = New Ratio – Old Ratio

References-

1. Mathematics and Statistics for Business – R. S. Bhardwaj – Excel Books.
2. Business Mathematics and Statistics – Subhanjali Chopra – Pearson publication.
3. Fundamentals of Business Mathematics and Statistics – ICAI – ICAI.
4. Business Mathematics and Statistics – Dr. J K Das, N Das – McGraw Hill Education.
5. Mathematical and statistical techniques, Dr.Abhilasha S. Magar & Manohar B. Bhagirath