UNIT 2

SIMULTANEOUS EQUATIONS

2.1 Meaning of Simultaneous Equation

Equation – Equations signify relation of equality between two algebraic expressions symbolized by the sign of equality ‘=’. In other words, an equation is statement which says that the two algebraic expressions are equal and is satisfied only for certain values of the variables.

Identify – When equality of two algebraic expressions hold true for all values of variables then it is called an identity.

Root of an Equation – The value of unknown or variable for which the equation is true is known as the root of the equation. To find the roots of an equation means to solve the equations.

Degree of an Equation – The degree of an equation is the highest exponent of the variable x or variables (x, y, …) present in the equation is called the degree of an equation.

Linear Equation – An equation which involves power of an unknown quantity not higher than unity (one) is called a linear equation.

One variable Linear Equation – A linear equation in one variable (x, say) in which the highest degree of the variable x is 1.

A linear equation in one variable is, in general, written as ax+by = c or ax = c. This equation is also called, “First degree equation in x” or simple equation.

Two variable equation – A linear equation in two variables (x, y, say) in which the highest degree of the variables x and y each is 1. A linear equation in two variables, is general, is written as

Ax+by+c = 0

Or

Ax+by=d.

Three variable equation – A linear equation in three variables (x, y, z, say) in which the highest degree of the variables x, y and z each is 1. A linear equation in three variables, in general, is written as a1x+b1y+c1z=d.

2.2 Characteristics of Simultaneous Equations

1) A system of linear equations in one variable is not taken under simultaneous equations.

2) The set of values of two variables x and y which satisfy each equation in the system of equations is called the solution of simultaneous equations.

The solutions of two variable linear simultaneous equations may be –

i) Infinitely many,

Ii) A unique solution, or

Iii) No solution.

3) For simultaneous equations –

a1x + b1y = c1 and a2x + b2y = c2

a. If 𝑎1𝑎2=𝑏1𝑏2=𝑘 𝑎𝑛𝑑 𝑐1=𝑘 C2 then there are infinitely many solutions.

b. If 𝑎1𝑎2=𝑏1𝑏2=𝑐1 ≠ kc2, then there is no solution.

c. If c2 ≠ 0, then c1 = kc2  𝑐1𝑐2=𝑘, ℎ𝑒𝑛𝑐𝑒

𝑎1𝑎2=𝑏1𝑏2=𝑐1𝑐2→𝑖𝑛𝑓𝑖𝑛𝑖𝑡𝑒𝑙𝑦 𝑚𝑎𝑛𝑦 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛𝑠 𝑎𝑛𝑑 𝑎1𝑎2=𝑏1𝑏2≠𝑐1𝑐2→𝑛𝑜 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛

d. If c1 and c2 both are zero (i.e., c1=0=c2)

2.3 Types of Simultaneous Equations

i) Linear Simultaneous Equations in two Variables – Two linear equations in two variables together are linear simultaneous equations in two variables, e.g.:

4x+y = 2

3x-5y = 18

Ii) Linear Simultaneous Equations in three Variables – Three linear equations in three variables together are linear simultaneous equations in three variables, e.g.:

3x+5y-7z = 13

4x+y-12z = 6

2x+9y-3z = 20

Iii) Specific type of Simultaneous Equations – The equations in other than linear form is called specific type equations, e.g.:

i)                   quadratic equation: ax2 + bx + c = 0

Ii)                 reciprocal equation: 𝑎𝑥+𝑏𝑦 =𝑐

Iii)              a 𝑦𝑥 + 𝑐=𝑏𝑦, 𝑒𝑡𝑐.

2.4 Calculations

Examples of using substitution to solve simultaneous equations:

1. 3x + y = 13
   5x -2y = 7
   
   The coefficient of y in Equation 1 is 1. So first we make y the subject of Equation 1:
   
   y = 13 - 3x
   
   Next, substitute this expression for y in Equation 2 and solve for x:

Finally, substitute the solution for x into the expression for y:

y = 13 - 3(3) = 4
y = 4

So the solution to the pair of simultaneous linear equations is (3,4).
 

2.     2x + 4y = 10
2x + y = 4

The coefficient of y in Equation 2 is 1. So first we make y the subject of Equation 2:

y = 4 - 2x

Next, substitute this expression for y in Equation 1 and solve for x:

Finally, substitute the solution for x into the expression for y:

y = 4 - 2(1) = 2
y = 2

So the solution to the pair of simultaneous linear equations is (1,2).
 

3.       x - 5y = 7
2x -4y = 8

The coefficient of x in Equation 1 is 1. So first we make x the subject of Equation 1:

x = 7 + 5y

Next, substitute this expression for x in Equation 2 and solve for y:

Finally, substitute the solution for y into the expression for x:

x = 7 + 5(-1) = 2
x = 2

So the solution to the pair of simultaneous linear equations is (2,-1).
 

4.     2x + 4y = 12
  x + 8y = 30

The coefficient of x in Equation 2 is 1. So first we make x the subject of Equation 2:

x = 30 - 8y

Next, substitute this expression for x in Equation 1 and solve for y:

Finally, substitute the solution for y into the expression for x:

x = 30 - 8(4) = -2
x = -2

So the solution to the pair of simultaneous linear equations is (-2,2).
 

5.     2x - 4y = 10
-4x+5y = -26

None of the coefficients are 1. So we can choose to make any variable the subject.
Let’s make x the subject of Equation 1:

x = (10 + 4y)/2
x = 5 + 2y

Next, substitute this expression for x in Equation 2 and solve for y:

-4(5 + 2y ) + 5y = -26
-20 - 8y + 5y = -26
-3y = -6
y = 2

Finally, substitute the solution for y into the expression for x:

x = 5 + 2(2) = 9
x = 9

So the solution to the pair of simultaneous linear equations is (9,2).
 

6.     6x + 2y = 10
10x - 3y = 12

None of the coefficients are 1. So we can choose to make any variable the subject.
Let’s make y the subject of Equation 2:

y = (12-10x)/(-3)
y = -4 + (10/3) x

Next, substitute this expression for y in Equation 1 and solve for x:

6x + 2(-4 + (10/3) x) = 10
6x - 8 + (20/3) x = 10
(38/3) x = 18
x = 18*(3/38) = 27/19

Finally, substitute the solution for x into the expression for y:

y = -4 + (10/3)/(27/19) = -4 + 270/57 = -228/57 = 270/57 = 42/57 = 14/19

So the solution to the pair of simultaneous linear equations is (27/19,5/19)

Examples of Solved problems of Simultaneous Equations using Elimination Method

1. Solve the following simultaneous equations by using the elimination method:

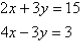
Solution:

Label the equations as follows:

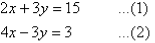
Notice that 3y appears on the left-hand side of both equations.  Adding the left-hand side of (1) and (2), and then the right-hand sides, gives:

Note:

We have added equals to equals, and addition eliminates y.

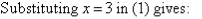
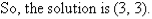
2.     Solve the following simultaneous equations by using the elimination method:

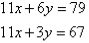
Solution:

Label the equations as follows:

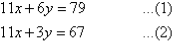
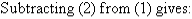
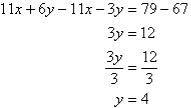
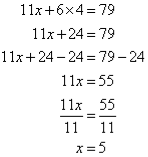
So, the solution is (5, 4)
 

3.    Solve the following simultaneous equations by using the elimination method:

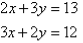
Solution:

Label the equations as follows:

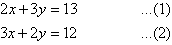
Multiplying (1) by 2 and (2) by 3 gives:

Subtracting (3) from (4) gives:

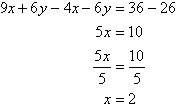
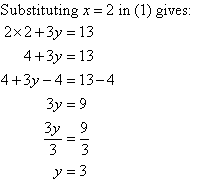
So, the solution is (2, 3).

Equations Containing Fractions

If either or both equations contain fractions, then it is desirable to remove the denominators before solving them simultaneously.

4.     Solve the following simultaneous equations by using the elimination method:

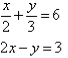
Solution:

Label the equations as follows:

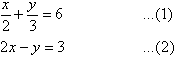
To simplify equation (1), multiply both sides by 6, the lowest common denominator of 2 and 3.

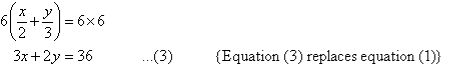
The equations are now:

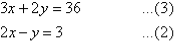
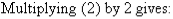
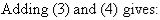
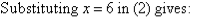
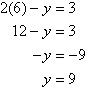
So, the solution is (6, 9).

2.5 Preparation of Invoice

After the dispatch of goods, the seller prepares an invoice of the goods sold in which the quantity and quality of goods and their price is mentioned. Discount, if any, is deducted from the total amount, to this are added the seller’s other expenses. Railway receipt number is also mentioned in the invoice if the goods have been sent by train.

Types of Invoice –

1) Local invoices – In these invoices only the cost of the goods less any trade discount is borne by the seller. All expenses of packing, cartage, loading and freight for carrying goods to the place of buyer are shown extra and charged to the buyer. It means that the cost includes cost of the goods only and all other expenses are extra and are recovered from the buyer.

2) At station invoice – This implies that all costs upto the stage of putting the goods at railway station will be borne by the seller and are included in the cost of goods but expenses beyond that, i.e., the railway fare, insurance, etc., will be borne by the buyer.

3) Free on Rails (FOR) invoices – Under this all the costs, i.e., cost of goods, cost of packing, carrying the goods to railway station, loading them in wagons, are borne by the seller and further expenses are borne by the buyer, i.e., they are charged over and above the cost of goods.

4) Cost and Freight (C and F) invoice – In such type of invoices it is presumed that cost which the seller is charging includes cost of goods, cost of packing, freight for carrying goods to the buyer and all other incidental expenses. All expenses other than above, i.e., insurance will be charged extra.

5) Cost, Insurance and freight, (CI & F) invoice – In such invoices cost charged by the seller includes cost of goods, cost of packing, freight and insurance. Other expenses are charged extra.

6) Franco invoice – In such invoices all costs upto putting the goods at the door of the buyer are borne by the seller, i.e., the price which he has quoted includes all expenses incurred in carrying the goods to the buyer’s place. For example, Franco cost invoice will mean that cost charged by the seller includes cost of the goods, cost of packing, freight, insurance and local transportation charges.

Preparation of Invoice – Invoice is prepared in duplicate. The original copy is sent to the buyer and the duplicate is kept for future reference.

The usual contents of the invoice are –

i) Name and address of the seller

Ii) No. And date of the invoice

Iii) No. Of the purchase order

Iv) Name and address of the buyer

v) Place where it has been made

Vi) Terms of trade

Vii) Details about quantity of goods like weight or length etc.

Viii) Date

Ix) Separate price of each item and total price.

x) Trade discount, if any.

Xi) Expenses incurred on sending the goods.

Xii) Advance payment received (if paid by the buyer)

Xiii) Net amount payable.

Xiv) Details about mode of sending the goods

Xv) Errors and omissions excepted

Xvi) Special information, if any

Xvii) Signature of the seller.

Uses of Invoice –

Following are the uses of invoice –

a) It informs the buyer about the price of the goods and other expenses he has to pay.

b) If the invoice reaches buyer before the goods, he can make arrangement for their resale.

c) The buyer can compare the invoice with his order.

d) After taking delivery of the goods he can compare the contents of the packages with the invoice and point discrepancy, if any to the seller.

e) Pay Octroi etc. on the basis of the invoice.

Necessary entries can be made in the books of accounts on the basis of invoice.

References

1. Https://www.mathsteacher.com.au/year10/ch04_simultaneous/03_elimination_method/elim.htm
2. Https://revisionmaths.com/gcse-maths-revision/algebra/simultaneous-equations
3. Https://www.allaboutcircuits.com/textbook/reference/chpt-4/solving-simultaneous-equations/