UNIT 3

ELEMENTARY MATRICES

3.1 Definition and calculations, types of matrices.

Matrices: some important definitions and some important results

Matrices have wide range of applications in various disciplines such as chemistry, Biology, Engineering, Statistics, economics, etc.

Matrices play an important role in computer science also.

Matrices are widely used to solving the system of linear equations, system of linear differential equations and non-linear differential equations.

First time the matrices were introduced by Cayley in 1860.

Definition-

A matrix is a rectangular arrangement of the numbers.

These numbers inside the matrix are known as elements of the matrix.

A matrix ‘A’ is expressed as-

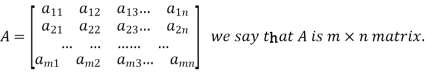
The vertical elements are called columns and the horizontal elements are rows of the matrix.

The order of matrix A is m by n or (m× n)

Notation of a matrix-

A matrix ‘A’ is denoted as-

A =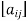

Where, i = 1, 2, …….,m and j = 1,2,3,…….n

Here ‘i’ denotes row and ‘j’ denotes column.

Types of matrices-

1. Rectangular matrix-

A matrix in which the number of rows is not equal to the number of columns, are called rectangular matrix.

Example:

A =

The order of matrix A is 2×3 , that means it has two rows and three columns.

Matrix A is a rectangular matrix.

2. Square matrix-

A matrix which has equal number of rows and columns, is called square matrix.

Example:

A =

The order of matrix A is 3 ×3 , that means it has three rows and three columns.

Matrix A is a square matrix.

3. Row matrix-

A matrix with a single row and any number of columns is called row matrix.

Example:

A =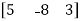

4. Column matrix-

A matrix with a single column and any number of rows is called row matrix.

Example:

A =

5. Null matrix (Zero matrix)-

A matrix in which each element is zero, then it is called null matrix or zero matrix and denoted by O

Example:

A =

6. Diagonal matrix-

A matrix is said to be diagonal matrix if all the elements except principal diagonal are zero

The diagonal matrix always follows-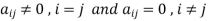

Example:

A =

7. Scalar matrix-

A diagonal matrix in which all the diagonal elements are equal to a scalar, is called scalar matrix.

Example-

A =

8. Identity matrix-

A diagonal matrix is said to be an identity matrix if its each element of diagonal is unity or 1.

It is denoted by – ‘I’

I =

9. Triangular matrix-

If every element above or below the leading diagonal of a square matrix is zero, then the matrix is known as a triangular matrix.

There are two types of triangular matrices-

(a) Lower triangular matrix-

If all the elements below the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.

Example:

A =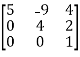

(b) Upper triangular matrix-

If all the elements above the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.

Example-

A =

Special types of matrices-

Symmetric matrix-

Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.

For example:

and

Example: check whether the following matrix A is symmetric or not?

A =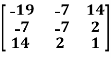 

Sol. As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.

So that, first we will find its transpose,

Transpose of matrix A ,

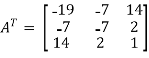
Here,

A =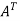

The matrix A is symmetric.

Example: Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.

Sol.  Suppose A is any square matrix.

Then,

A =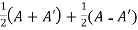

Now,

(A + A’)’ = A’ + A

A+A’ is a symmetric matrix.

Also,

(A - A’)’ = A’ – A

Here A’ – A is an anti – symmetric matrix

So that,

Square matrix = symmetric matrix + anti-symmetric matrix

Hermitian matrix:

A square matrix A = 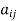is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.

It means,

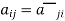
For example:

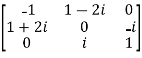
Necessary and sufficient condition for a matrix A to be hermitian –

A = (͞A)’

Skew-Hermitian matrix-

A square matrix A = 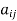is said to be hermitian matrix if every element of A is equal to negative conjugate complex j-ith element of A.

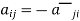
Note- all the diagonal elements of a skew hermitian matrix are either zero or pure imaginary.

For example:

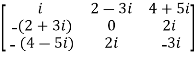
The necessary and sufficient condition for a matrix A to be skew hermitian will be as follows-

- A = (͞A)’

Note:   A Hermitian matrix is a generalization of a real symmetric matrix and also every real symmetric matrix is Hermitian.

Similarly a Skew- Hermitian matrix is a generalization of a  Skew symmetric matrix  and also every Skew- symmetric matrix  is Skew –Hermitian.

Theorem: Every square complex   matrix   can   be uniquely   expressed as sum hermitian and skew-hermitian matrix.

Or If A   is given square complex matrix then 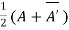 is   hermitian and  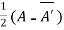is skew-hermitian matrices.

Example1: Express the matrix A as sum of hermitian and skew-hermitian matrix where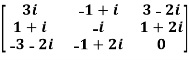

Let A =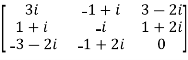

Therefore 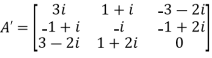   and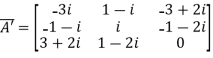

Let

Again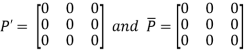

Hence P is a hermitian matrix.

Let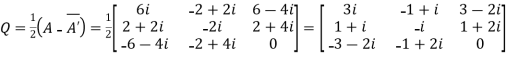 

Again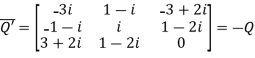

Hence Q is a skew- hermitian matrix.

We Check

P +Q=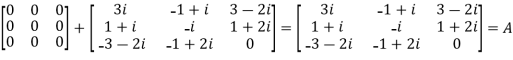

Hence proved.

Example2: If A = 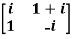  then show that

(i) 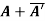is hermitian matrix.

(ii)   is  skew-hermitian matrix.

Sol.

Given   A =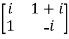

Then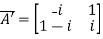 

Let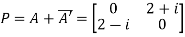

Also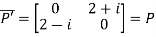  

Hence P is a Hermitian matrix.

Let

Also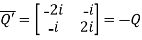

Hence Q is a   skew-hermitian matrix.

Skew-symmetric matrix-

A square matrix A is said to be skew symmetrix matrix if –

1.  A’ = -A,    [ A’ is the transpose of A]

2.all the main diagonal elements will always be zero.

For example-

A =

This is skew symmetric matrix, because transpose of matrix A is equals to negative A.

Example: check whether the following matrix A is symmetric or not?

A =

Sol. This is not a skew symmetric matrix, because the transpose of matrix A is not equals to  -A.

-A = A’

Orthogonal matrix-

Any square matrix A is said to be an orthogonal matrix if the product of the matrix A and its transpose is an identity matrix.

Such that,

A. A’ = I

Matrix × transpose of matrix = identity matrix

Note- if |A| = 1, then we can say that matrix A is proper.

Examples:                 and              are the form of orthogonal matrices.

Unitary matrix-

A square matrix A is said to be unitary matrix if the product of the transpose of the conjugate of matrix A and matrix itself  is an identity matrix.

Such that,

( ͞A)’. A = I

For example:

And its

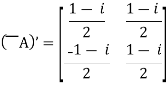
Then  (͞A)’ . A = I

So that we can say that matrix A is said to be a unitary matrix.

Key takeaways-

1. The matrices were introduced by Cayley in 1860.
2. A matrix ‘A’ is denoted as-

A =

Where, i = 1, 2, …….,m and j = 1,2,3,…….n

Here ‘i’ denotes row and ‘j’ denotes column.

3.     Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.

4.      Square matrix = symmetric matrix + anti-symmetric matri

5.     A square matrix A = is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.

6.     All the diagonal elements of a skew hermitian matrix are either zero or pure imaginary.

7.      A Hermitian matrix is a generalization of a real symmetric matrix and also every real symmetric matrix is Hermitian

8.     Every square complex   matrix   can   be uniquely   expressed as sum hermitian and skew-hermitian matrix.

9.     A square matrix A is said to be skew symmetrix matrix if –

(a) A’ = -A,    [ A’ is the transpose of A]

(b)  all the main diagonal elements will always be zero.

10. Any square matrix A is said to be an orthogonal matrix if the product of the matrix A and its transpose is an identity matrix.

11. if |A| = 1, then we can say that matrix A is proper.

12. A square matrix A is said to be unitary matrix if the product of the transpose of the conjugate of matrix A and matrix itself  is an identity matrix.

Matrix operation ( Addition, scalar multiplication, matrix multiplication, transpose of a matrix)

Algebra on Matrices:

1. Addition and subtraction of matrices:

Addition and subtraction of matrices is possible if and only if they are of same order.

We add or subtract the corresponding elements of the matrices.

Example: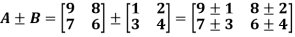

Example: Add .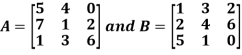

Sol.

A + B =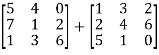

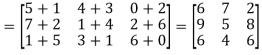
2.     Scalar multiplication of matrix:

In this we multiply the scalar or constant with each element of the matrix.

Example: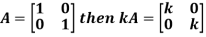

3.     Multiplication of matrices: Two matrices can be multiplied only if they are conformal i.e. the number of column of first matrix is equal to the number rows of the second matrix.

Example: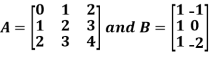

Then

4.     Power of Matrices: If A is A square matrix then

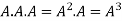and so on.

If 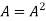where A is square matrix then it is said to be idempotent.

5. Transpose of  a  matrix: The  matrix  obtained  from  any  given  matrix A ,  by interchanging rows  and   columns is  called the  transpose of  A and is  denoted  by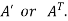

The transpose of matrix 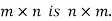 Also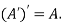 

Note: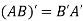

6. Trace of a matrix-

Suppose A be a square matrix, then the sum of its diagonal elements is known as trace of the matrix.

Example- If we have a matrix A-

Then the trace of A = 0 + 2 + 4 = 6

Key takeaways-

1. Addition and subtraction of matrices is possible if and only if they are of same order.
2. Two matrices can be multiplied only if they are conformal i.e. the number of column of first matrix is equal to the number rows of the second matrix.
3. If where A is square matrix then it is said to be idempotent.
4. The  matrix  obtained  from  any  given  matrix A ,  by interchanging rows  and   columns is  called the  transpose of  A and is  denoted  by
5. :

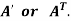
If A be a square matrix, then the sum of its diagonal elements is known as trace of the matrix