UNIT 4
LOGARITHMS AND ANTILOGARITHMS
A logarithm is the power to which a number must be raised in order to get some other number. For example, the base ten logarithm of 100 is 2, because ten raised to the power of two is 100:
Log 100 = 2
Because
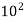 = 100
= 100
This is an example of a base-ten logarithm. We call it a base ten logarithm because ten is the number that is raised to a power. The base unit is the number being raised to a power. There are logarithms using different base units. If you wanted, you could use two as a base unit. For instance, the base two logarithm of eight is three, because two raised to the power of three equals eight:
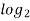 8 = 3
8 = 3
Because
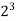 = 8
= 8
In general, you write log followed by the base number as a subscript. The most common logarithms are base 10 logarithms and natural logarithms; they have special notations. A base ten log is written
Log
And a base ten logarithmic equation is usually written in the form:
Log a = r
A natural logarithm is written
Ln
And a natural logarithmic equation is usually written in the form:
Ln a = r
So, when you see log by itself, it means base ten log. When you see ln, it means natural logarithm (we'll define natural logarithms below). In this course only base ten and natural logarithms will be used.
Properties of Logarithms
 mn =
mn =  m +
m + 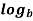 n
n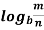 =
= 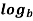 m -
m -  n
n = p
= p 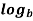 n
n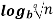 =
= 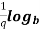 n
n n =
n = 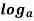 n
n 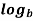 a
a- Zero Exponent Rule:
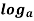 1 = 0
1 = 0
1. Express 53 = 125 in logarithm form.
Solution:
53 = 125
As we know,
ab = c ⇒ logac=b
Therefore;
Log5125 = 3
2. Express log101 = 0 in exponential form.
Solution:
Given, log101 = 0
By the rule, we know;
Logac=b ⇒ ab = c
Hence,
100 = 1
3. Find the log of 32 to the base 4.
Solution: log432 = x
4x = 32
(22)x = 2x2x2x2x2
22x = 25
2x=5
x=5/2
Therefore,
Log432 =5/2
4. Find x if log5(x-7)=1.
Solution: Given,
Log5(x-7)=1
Using logarithm rules, we can write;
51 = x-7
5 = x-7
x=5+7
x=12
5. If logam=n, express an-1 in terms of a and m.
Solution:
Logam=n
an=m
an/a=m/a
an-1=m/a
6. Solve for x if log(x-1) +log(x+1) =log21
Solution: log(x-1) +log(x+1) =log21
Log(x-1) +log(x+1) =0
Log[(x-1) (x+1)] =0
Since, log 1 = 0
(x-1) (x+1) = 1
x2-1=1
x2=2
x=± √2
Since, log of negative number is not defined.
Therefore, x=√2
7. Express log (75/16)-2log (5/9) +log (32/243) in terms of log 2 and log 3.
Solution: log (75/16)-2log (5/9) +log (32/243)
Since, nlogam=logamn
⇒log (75/16)-log (5/9)2+log (32/243)
⇒log (75/16)-log (25/81) +log (32/243)
Since, logam-logan=loga(m/n)
⇒log [(75/16) ÷ (25/81)] +log (32/243)
⇒log [(75/16) × (81/25)] +log (32/243)
⇒log (243/16) +log (32/243)
Since, logam+logan=logamn
⇒log (32/16)
⇒log2
8. Express 2logx+3logy=log a in logarithm free form.
Solution: 2logx+3logy=log a
Logx2+logy3=log a
Logx2y3=log a
x2y3=log a
9. Prove that: 2log (15/18)-log (25/162) +log (4/9) =log2
Solution: 2log (15/18)-log (25/162) +log (4/9) =log2
Taking L.H.S.:
⇒2log (15/18)-log (25/162) +log (4/9)
⇒log (15/18)2-log (25/162) +log (4/9)
⇒log (225/324)-log (25/162) +log (4/9)
⇒log [(225/324) (4/9)]-log (25/162)
⇒log [(225/324) (4/9)]/ (25/162)
⇒log (72/36)
⇒log2 (R.H.S)
10. Express log10(2+1) in the form of log10x.
Solution: log10(2+1)
=log102+log101
=log10(2×10)
=log1020
11. Find the value of x, if log10(x-10) =1.
Solution: Given, log10(x-10) =1.
Log10(x-10) = log1010
x-10 = 10
x=10+10
x=20
12. Find the value of x, if log(x+5) +log(x-5) =4log2+2log3
Solution: Given,
Log(x+5) +log(x-5) =4log2+2log3
Log(x+5) (x-5) = 4log2+2log3 [log mn=log m+log n]
Log(x2-25) = log24+log32
Log(x2-25) = log16+log9
Log(x2-25) =log (16×9)
Log(x2-25) =log144
x2-25=144
x2=169
x=±√169
x=±13
13. Solve for x, if log(225/log15) = log x
Solution: log x = log(225/log15)
Log x=log [(15×15)]/log15
Log x = log 152/log 15
Log x = 2log 15/log 15
Log x = 2
Or
Log10x=2
102=x
x=10×10
x=100
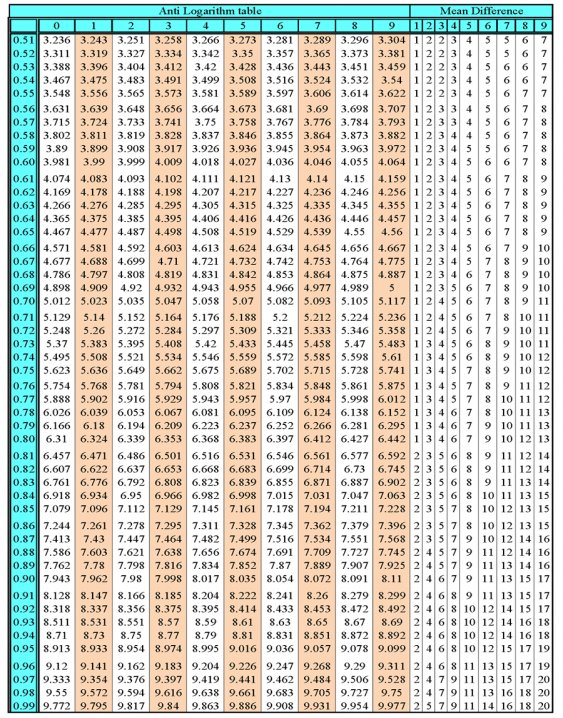
Anti-Logarithms (Antilog)
The anti-logarithm of a number is the inverse process of finding the logarithms of the same number. If x is the logarithm of a number y with a given base b, then y is the anti-logarithm of (antilog) of x to the base b.

Natural Logarithms and Anti-Logarithms have their base as 2.7183. The Logarithms and Anti-Logarithms with base 10 can be converted into natural Logarithms and Anti-Logarithms by multiplying it by 2.303.
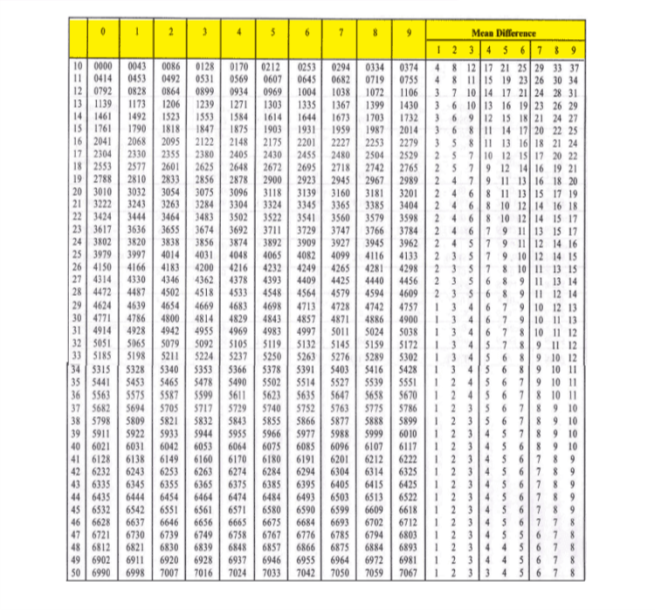
Anti-Logarithmic Table
To find the anti-logarithm of a number we use an anti-logarithmic table. Below are the steps to find the antilog.
- The first step is to separate the characteristic and the mantissa part of the number.
- Use the antilog table to find a corresponding value for the mantissa. The first two digits of the mantissa work as the row number and the third digit is equal to the column number. Note this value.
- The antilog table also includes columns which provide the mean difference. For the same row of the mantissa, the column number in the mean difference is equal to the fourth digit. Note this value.
- Add the values so obtained.
- In the characteristic add one. This value shows the place to put the decimal point. The decimal point is inserted after that many digits from the left.
Solved Examples on Logarithms and Anti-Logarithms
- Problem: Find the value of log 2.8726.
Solution: Here the number of digit to the left of the decimal is 1 so the value of the characteristic will be one less than one i.e., 0.
From the log table, the value of 2.8726 is 0.45827. Adding the values of mantissa and the characteristic we find the value of the logarithm.
So, log 2.8725 = 0 + 0.45827 = 0.45827.
2. Problem: Calculate the antilog of 3.6552.
Solution: Here we need to find the number whose logarithm is 3.655. From the antilog table, the value corresponding to the row 65 and column 5 is 4508.
The mean difference column for the value 2 is 2. Adding these two values, we have 4518 + 2 = 4520.
The decimal point is placed in 3 + 1 = 4 digits from the left. So, antilog 3.6552 = 4520.0
3. If log x = -2.0258, find x.
Solution:
In order to find the value of x using antilog-table, the decimal part (i.e., the mantissa) must be made positive. For this we proceed as follows:
log x = -2.0258 = - 3 + 3 - 2.0258
= - 3 + .9742 =3.9742
Therefore, x = antilog 3.9742.
Now, from antilog table we get the number corresponding to the mantissa
.9742 as (9419 + 4) = 9423.
Again the characteristic in log x is (- 3).
Hence, there should be two zeroes between the decimal point and the first significant digit in the value of x.
Therefore, x = .009423.
Key Takeaways:
- A logarithm is the power to which a number must be raised in order to get some other number.
- The anti-logarithm of a number is the inverse process of finding the logarithms of the same number. If x is the logarithm of a number y with a given base b, then y is the anti-logarithm of (antilog) of x to the base b.
Calculation of interest is one of the most basic uses of mathematics in finance.
We can define the simple interest as- “the price has to be paid for the use of a certain amount of money or principal for certain period, is called interest”
Amount- This is the sum of the principal and the interest at any time.
The rate of interest is denoted by ‘i’.
Let the principal is 100 rs. And the interest is 8 then we can say that the rate of interest is 8 percent per annum or we can write it as r = 8%
Suppose ‘P’ is the principal and ‘n’ is the time for which the principal is given and ‘r’ be the rate of interest per annum
‘I’ be the amount of interest
And ‘i’ be the rate of interest per unit
Then-
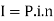
Here- i = r/100
We can calculate the amount as-
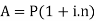
Example: Sushmita invested 5000rs. At the rate of 8 per cent per annum then what will be the value of the amount she invested in 5 years.
Sol.
Here P = 5000, i = 8/100 = 0.08, n = 5, now
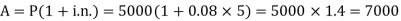
Hence the required amount is - 7000
Example: Find out the simple interest on 5600 rs. At 12 percent per annum from July 15 to September 26, 2020.
Sol.
Here we calculate the time-
Total days from july 15 to sept 26 = 73 days or 73/365 = 1/5 years
And P = 5600, i = 12/100 = 0.12
Simple interest = P.i.n. = 5600 
Hence the simple interest is – 134.40
Example: Harpreet invests 1200rs. At 10 percent per annum for some time and it becomes 1560 then find the principal when that will become 2232 at 8 percent p.a. In the same time.
Sol.
Here in first situation- P = 1200, A = 1560 and i = 0.10
So that,
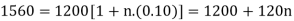
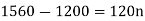
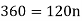
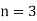
In second situation-
A = 2232, n = 3, i = 0.08
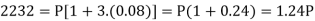


Compound interest-
In compound interest, the principal does not remain same but increases at the end of each interest period.
Let-
P- Principal
A - Amount
i = interest on re. 1 for a year
n = interest period
Then the amount can be calculated as-
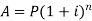
And

Note- By using algorithm the above formula can be written as-
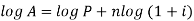
Note- if the compound interest is paid half-yearly, quarterly, monthly instead of a year there will be different formulae as given in the table below-
Time | Amount |
Annually | 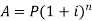 |
Half-yearly |  |
Quarterly | 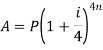 |
Example: Aman invests 1000 rupees at 5 percent p.a for four years then find the compound interest on it.
Sol.
Here P = 1000, i = 0.05 and n = 4
Then we know that-
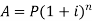
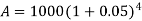
On taking log, we get-
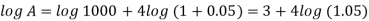
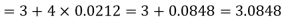
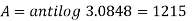
Compound interest will be-
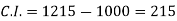
Which is the required answer.
Example:A sum of money invested at C.I. Payable yearly amounts to 10, 816 rs. At the end of the second year and to 11,248.64 rs. At the end of the third year. Find the rate of interest and the sum.
Sol.
Here A1 = 10,816, n = 2, and A2 = 11,248.64, n = 3
We know that
A = P (1 + i)n we get,
10,816 = 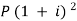 … (i)
… (i)
11,248.64 =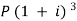 … (ii)
… (ii)
Here on dividing equation (2) by (1)-
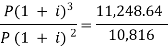
We get-
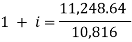
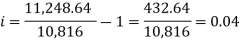
And
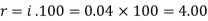
Hence the rate is 4 percent.
Now from first equation-
10,816 = 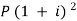
Or
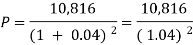
Now-
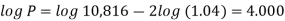
P = antilog 4.000 = 10,000
Therefore they require answer- 10,000
Nominal and effective rate of interest-
Nominal rate of interest is the rate of interest per annum which is compounded yearly, half yearly, quarterly, monthly, n times in a year or continuously.
Effective rate of interest is the rate of interest per annum compounded only once in a year.
There is a relationships between nominal and effective rate of interest under two different conditions-
- If compounding is ‘n’ times in a year-


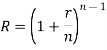
Where ‘r’ is nominal rate and ‘R’ is effective rate.
2. If compounding is continuous-
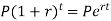
Or
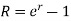
Relationship between two nominal rates-
If interest is compounded quarterly at 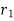 percent and the interest is compounded half yearly at
percent and the interest is compounded half yearly at  percent, then the relationship between the two is-
percent, then the relationship between the two is-
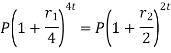
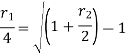
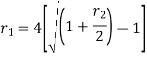
Example: Ronak deposited Rs. 10,000 in a bank for 3 years. Bank gives two offers either 10 percent compounded quarterly or 8% compounded continuously, then which offer is preferable for Ronak?
Sol.
Balance after three years under first offer-
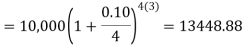
Balance after 3 years under second offer-
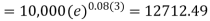
So that we can conclude that the first offer is preferable for Ronak.
Key takeaways-
- Amount- This is the sum of the principal and the interest at any time.
- We calculate the amount as-
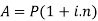
3. Compound interest-
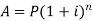
4. Nominal rate- Nominal rate of interest is the rate of interest per annum which is compounded yearly, half yearly, quarterly, monthly, n times in a year or continuously.
5. Effective rate- Effective rate of interest is the rate of interest per annum compounded only once in a year.
6. 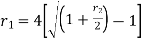
References
- Https://byjus.com/maths/antilog-table/
- Https://www.mathsisfun.com/algebra/logarithms.html
- Https://tutorial.math.lamar.edu/classes/alg/logfunctions.aspx
Logarithm Table
Anti-Logarithm Table