UNIT 5
AVERAGES
Mean
- The mean is the arithmetic average, also called as arithmetic mean.
- Mean is very simple to calculate and is most commonly used measure of the center of data.
- Means is calculated by adding up all the values and divided by the number of observation.
Computation of sample mean -
If X1, X2, ………………Xn are data values then arithmetic mean is given by
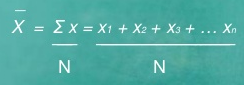
Computation of the mean for ungrouped data
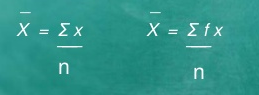
Example 1 – The marks obtained in 10 class test are 25, 10, 15, 30, 35

 The mean = X = 25+10+15+30+35 = 115 =23
The mean = X = 25+10+15+30+35 = 115 =23
5 5
Analysis – The average performance of 5 students is 23. The implication is that students who got below 23 did not perform well. The students who got above 23 performed well in exam.
Example 2 – Find the mean
Xi | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Freq (Fi) | 2 | 5 | 12 | 17 | 14 | 6 | 3 |
Xi | Freq (Fi) | XiFi |
9 | 2 | 18 |
10 | 5 | 50 |
11 | 12 | 132 |
12 | 17 | 204 |
13 | 14 | 182 |
14 | 6 | 84 |
15 | 3 | 45 |
| Fi = 59 | XiFi= 715 |
|
|
|
Then, N = ∑ fi = 59, and ∑fi Xi=715
 X = 715/59 = 12.11
X = 715/59 = 12.11
Mean for grouped data/ Weighted Arithmetic Mean
Grouped data are the data that are arranged in a frequency distribution
Frequency distribution is the arrangement of scores according to category of classes including the frequency.
Frequency is the number of observations falling in a category
The formula in solving the mean for grouped data is called midpoint method. The formula is

 Where, X = Mean
Where, X = Mean
Xm = midpoint of each class or category
f = frequency in each class or category
∑f Xm = summation of the product of fXm
Example 3 – the following data represent the income distribution of 100 families. Calculate mean income of 100 families?
Income | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
No. Of families | 8 | 12 | 25 | 22 | 16 | 11 | 6 |
Solution:
Income | No. Of families | Xm (Mid point) | FXm |
30-40 | 8 | 35 | 280 |
40-50 | 12 | 34 | 408 |
50-60 | 25 | 55 | 1375 |
60-70 | 22 | 65 | 1430 |
70-80 | 16 | 75 | 1200 |
80-90 | 11 | 85 | 935 |
90-100 | 6 | 95 | 570 |
| n = 100 |
| ∑f Xm = 6198 |

X = ∑f Xm/n = 6330/100 = 63.30
Mean = 63.30
Example 4 – Calculate the mean number of hours per week spent by each student in texting message.
Time per week | 0 - 5 | 5 - 10 | 10 - 15 | 15 - 20 | 20 - 25 | 25 – 30 |
No. Of students | 8 | 11 | 15 | 12 | 9 | 5 |
Solution:
Time per week (X) | No. Of students (F) | Mid point X | XF |
0 - 5 | 8 | 2.5 | 20 |
5 – 10 | 11 | 7.5 | 82.5 |
10 - 15 | 15 | 12.5 | 187.5 |
15 - 20 | 12 | 17.5 | 210 |
20 - 25 | 9 | 22.5 | 202.5 |
25 – 30 | 5 | 27.5 | 137.5 |
| 60 |
| 840 |
Mean = 840/60 = 14
Example 5 –
The following table of grouped data represents the weights (in pounds) of all 100 babies born at a local hospital last year.
Weight (pounds) | Number of Babies |
[3−5) | 8 |
[5−7) | 25 |
[7−9) | 45 |
[9−11) | 18 |
[11−13) | 4 |
Solution:
Weight (pounds) | Number of Babies | Mid point X | XF |
[3−5) | 8 | 4 | 32 |
[5−7) | 25 | 6 | 150 |
[7−9) | 45 | 8 | 360 |
[9−11) | 18 | 10 | 180 |
[11−13) | 4 | 12 | 48 |
| 100 |
| 770 |
Mean = 770/100 = 7.7
Geometric mean
Geometric mean is a type of mean or average, which indicates the central tendency of a set of numbers by using the product of their values.
Definition
The Geometric Mean (G.M) of a series containing n observations is the nth root of the product of the values.
For ungrouped data
 Geometric Mean, GM = Antilog ∑logxi
Geometric Mean, GM = Antilog ∑logxi
N
Example 1 – find the G.M of the values
X | Log X |
45 | 1.653 |
60 | 1.778 |
48 | 1.681 |
65 | 1.813 |
Total | 6.925 |
 GM = Antilog ∑logxi
GM = Antilog ∑logxi
N
= Antilog 6.925/4
= Antilog 1.73
= 53.82
For grouped data
 Geometric Mean, GM = Antilog ∑ f logxi
Geometric Mean, GM = Antilog ∑ f logxi
N
Example 2 – calculate the geometric mean
X | f |
60 – 80 | 22 |
80 – 100 | 38 |
100 – 120 | 45 |
120 – 140 | 35 |
|
|
Solution
X | f | Mid X | Log X | f log X |
60 – 80 | 22 | 70 | 1.845 | 40.59 |
80 – 100 | 38 | 90 | 1.954 | 74.25 |
100 – 120 | 45 | 110 | 2.041 | 91.85 |
120 – 140 | 35 | 130 | 2.114 | 73.99 |
Total | 140 |
|
| 280.68 |
 GM = Antilog ∑ f logxi
GM = Antilog ∑ f logxi
N
= antilog 280.68/140
= antilog 2.00
GM = 100
Example 3 – calculate geometric mean
Class | Frequency |
2-4 | 3 |
4-6 | 4 |
6-8 | 2 |
8-10 | 1 |
Solution
Class | Frequency | x | Log x | Flogx |
2-4 | 3 | 3 | 1.0986 | 3.2958 |
4-6 | 4 | 5 | 1.2875 | 6.4378 |
6-8 | 2 | 7 | 0.5559 | 3.8918 |
8-10 | 1 | 9 | 0.2441 | 2.1972 |
| 10 |
|
| 15.8226 |
 GM = Antilog ∑ f logxi
GM = Antilog ∑ f logxi
N
= antilog 15.8226/10
= antilog 1.5823
GM = 4.866
Harmonic mean
Harmonic mean is quotient of “number of the given values” and “sum of the reciprocals of the given values
For ungrouped data
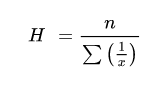
Example 1 - Calculate the harmonic mean of the numbers 13.2, 14.2, 14.8, 15.2 and 16.1
Solution
X | 1/X |
13.2 | 0.0758 |
14.2 | 0.0704 |
14.8 | 0.0676 |
15.2 | 0.0658 |
16.1 | 0.0621 |
Total | 0.3147 |
H.M of X = 5/0.3147 = 15.88
Example 2 - Find the harmonic mean of the following data {8, 9, 6, 11, 10, 5} ?
X | 1/X |
8 | 0.125 |
9 | 0.111 |
6 | 0.167 |
11 | 0.091 |
10 | 0.100 |
5 | 0.200 |
Total | 0.794 |
H.M of X = 6/0.794 = 7.560
For grouped data
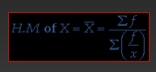
Example 3 - Calculate the harmonic mean for the below data
Marks | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 |
F | 2 | 3 | 11 | 20 | 32 | 25 | 7 |
Solution
Marks | X | F | F/X |
30-39 | 34.5 | 2 | 0.0580 |
40-49 | 44.5 | 3 | 0.0674 |
50-59 | 54.4 | 11 | 0.2018 |
60-69 | 64.5 | 20 | 0.3101 |
70-79 | 74.5 | 32 | 0.4295 |
80-89 | 84.5 | 25 | 0.2959 |
90-99 | 94.5 | 7 | 0.0741 |
Total |
| 100 | 1.4368 |
HM = 100/1.4368 = 69.59
Example 4 – find the harmonic mean of the given class
Ages | 4 | 5 | 6 | 7 |
No. Of students | 6 | 4 | 10 | 9 |
Solution
X | F | f/x |
4 | 6 | 1.50 |
5 | 4 | 0.80 |
6 | 10 | 1.67 |
7 | 9 | 1.29 |
| 29.00 | 5.25 |
HM = 29/5.25 = 5.5
Example 5 – calculate harmonic mean
Class | Frequency |
2-4 | 3 |
4-6 | 4 |
6-8 | 2 |
8-10 | 1 |
Solution
Class | Frequency | x | f/x |
2-4 | 3 | 3 | 1 |
4-6 | 4 | 5 | 0.8 |
6-8 | 2 | 7 | 0.28 |
8-10 | 1 | 9 | 0.11 |
| 10 |
| 2.19 |
Harmonic mean = 10/2.19 = 4.55
Merits of mean
- It is rigidly defined
- It is easy to understand and easy to calculate
- It is based upon all values of the given data
- It is capable of future mathematical treatment
- It is not much affected by sampling fluctuation
Demerits of mean
- It cannot be calculated if any observation are missing
- It cannot be calculated for open end classes
- It is effected by extreme values
- It cannot be located graphically
- It may be number which is not present in the data
Terms and formulae, problem involving cost price, selling price, trade discount, cash discount
Cost Price (CP) - The price at which an article is purchased.
Selling Price (SP) - This is the price at which an article is sold.
Profit - If the selling price is more than the cost price, then there will be profit
Profit = Selling price (SP) – Cost price (CP)
Profit % = (profit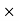 100)/CP
100)/CP
Loss - If the selling price is less than the cost price, then there will be loss
Loss = Cost price (CP) – Selling price (SP)
Loss% = (Loss  100)/CP
100)/CP
Marked Price - This is the price marked as the selling price on an article, also known as the listed price
Note- Profit or Loss is always calculated on the cost price.
Discount: This is the reduction in price offered on the marked or listed price.
Example: Suppose the profit percentage is 80% of the cost. If the cost further increases by 20% but the selling price remains the same, how much is the decrease in profit percentage?
Sol.
Let us suppose
CP = Rs. 100.
Then Profit = Rs. 80 and selling price = Rs. 180.
The cost increases by 20% → New CP = Rs. 120, SP = Rs. 180.
Profit % = 60/120 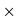 100 = 50%.
100 = 50%.
Therefore, Profit decreases by 30%.
Example: A dishonest shopkeeper sells his grocery using weights 15% less than the true weights and makes a profit of 20%. Find his total gain percentage.
Sol.
Suppose 1 kg of grocery bag.
Its actual weight is 85% of 1000 gm = 850 gm.
Let the cost price of each gram be Re. 1. Then the CP of each bag = Rs. 850.
SP of 1 kg of bag = 120% of the true CP
Therefore, SP = 120/100 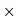 1000 = Rs. 1200
1000 = Rs. 1200
Gain = 1200 – 850 = 350
Hence Gain % = 350/850  100 = 41.17%
100 = 41.17%
Example: A shopkeeper offers a discount of 20% on the selling price. On a special sale day, he offers an extra 25% off coupon after the first discount. If the article was sold for Rs. 3600, find the marked price of the article
Sol.
Let the marked price of the article be x.
First a 20% discount was offered, on which another 25% discount was offered.
So, 75% of 80% of x = 3600
75/100 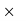 80/100
80/100  x = 3600 → x = 6000.
x = 3600 → x = 6000.
So the article was marked at Rs. 6000.
Example: The cost price of 30 articles is equal to the selling price of 40 articles. What is the profit or loss percentage?
Sol.
CP of 30 articles = SP of 40 articles Or, CP/SP = 30/40 =3/4
Or, 1 – CP/SP = 1- 3/4 = 1/4
So, Loss percentage
= (l – CP/SP) x 100 = 1/4x 100 = 25%
Trade discount-
Trade discount is a certain percentage a manufacturer is willing to reduce its list price for wholesalers or retailers.
Trade discounts are given to wholesalers that order large quantities of a product as well as retailers with good relationships with the manufacturer. Purchase discounts or Cash discount are based on payment plans not order quantities.
Trade discounts are offered on bulk purchases by traders, wholesalers, distributors or retailers and not to the end consumers.
Trade discounts are generally offered at varied rates depending on the volume of sale
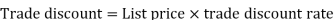
And

Example: Sweety purchases a set of toys that lists for Rs. 950 and it has a trade discount of 30%, then find the net price.
Sol.
As we know that-
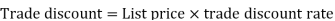
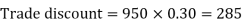
Then
Net price = 950 – 285 = 665
Example: If Raheem will buy a table that lists for Rs. 2000 and it has a trade discount of 50%. Then how much will he pay?
Sol.
As we know that-

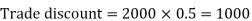
Then
Net price = 2000 – 1000 = 1000
Cash discountis allowed to stimulate instant payment of the goods purchased.
Cash Discount is referred to as a discount, allowed to customers by the seller at the time of making the payment of purchases, as a reduction in the invoice price of the commodity.
Both the buyers and sellers keep a proper record of such discount in their books of accounts.
Sellers offer cash discounts to their buyers as an incentive to encourage early payment.
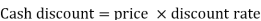
Ordinary dating method-
A credit term of [2/10, n/30] means that you will get a discount of 2% if you clear your account within 10 days
Example: A person received an invoice for Rs. 3,000 dated 22 November 2019 with terms [2/10, n/30]. He paid the whole amount on 30 November 2019. How much did he effectively paid for the bill?
Sol.
- Date of Invoice: 22nd November 2019
- Day 1 of the cash discount period. : 23rd November 2019
- Last day of the Cash discount period: 31st November 2019
- Date of payment: 30th November 2019
Cash discount.= Price  Discount rate
Discount rate
= Rs. 3,000  2/100
2/100
= Rs. 60
Amount effectively paid by the person = Bill value - Cash discount
= 3,000 - 60
= Rs. 2,940
Key takeaways-
- Cost Price (CP) - The price at which an article is purchased
- Selling Price (SP) - This is the price at which an article is sold
- Profit = Selling price (SP) – Cost price (CP)
- Profit = Selling price (SP) – Cost price (CP)
- Loss = Cost price (CP) – Selling price (SP)
- Loss% = (Loss
 100)/CP
100)/CP - Marked Price - This is the price marked as the selling price on an article, also known as the listed price
- Discount: This is the reduction in price offered on the marked or listed price.
- Trade discount is a certain percentage a manufacturer is willing to reduce its list price for wholesalers or retailers.
- Trade discounts are generally offered at varied rates depending on the volume of sale

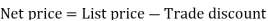
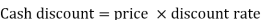
Introduction to commission and brokerage- problems on commission and brokerage
The amount received by the agency for providing its services is known as ‘brokerage’ or ‘commission’.
For example- placement agencies, marriage bureaus etc.
An individual can also run this type of business
Note- An individual who acts as a ‘middle man’ between a seller and buyer is known as broker.
Brokerage is paid by purchaser, Commission is paid by seller. Therefore
Net amount paid by purchaser = Sale price + brokerage
Net amount received by seller = Sale price - commission
Commission % = Commission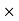 100 /Selling price
100 /Selling price
Selling Price = Commission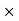 100/ Commission %
100/ Commission %
Commission (Brokerage) = Commission%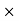 Selling price/100
Selling price/100
Example: The Price of a book is Rs. 15.75. A book seller sells 1200 books and pays Rs 17,860.50 to the book publisher after deducting his commission.
Find the commission rate.
Sol.
Here we have total commission,
We have to find the total sale price of books.
The total sale price of books = Number of Books 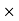 Price = 1200
Price = 1200 15.75 =18900
15.75 =18900
Commission = Sale price – Amount paid to the Publisher = 18900-17860.5 = 1039.5
Commission % = Commission 100 /Selling price = 1039.5
100 /Selling price = 1039.5 100/18900 = 5.5%
100/18900 = 5.5%
Example: Mahesh sold his car for Rs.68,000 with the help of an agent. If the commission paid by Mahesh is Rs 2550. Find rate of commission, and the net amount received by the Mahesh.
Sol.
Commission % = Commission 100 /Selling price = 2550
100 /Selling price = 2550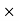 100/68000 = 3.75%
100/68000 = 3.75%
Net amount received by farmer = Sale price – Commission = 68000-2550 = Rs65, 450
Example: An agency pays 15% commission to a notebook distributor. The price of each notebook is Rs 3. If he sells 50 copies of notebook every day, find how much commission he receives in a month and also net amount received by the Agency?
Sol.
Price of each news paper = Rs 3.
Sale price for a day = Number copies sold in day  price of Cost of news paper = 50
price of Cost of news paper = 50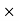 3 = Rs 150
3 = Rs 150
Sale price for a year = Number of days Sale price for a day = 30
Sale price for a day = 30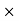 150 = 450 Rs
150 = 450 Rs
Commission = Commission%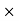 Selling price/100 = 15
Selling price/100 = 15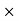 450/100 = 67.5 Rs.
450/100 = 67.5 Rs.
Net amount received by agency = selling price – commission = 450 -67.5 = 382.5 Rs
Key takeaways-
- Net amount paid by purchaser = Sale price + brokerage
Net amount received by seller = Sale price - commission
2. Commission % = Commission 100 /Selling price
100 /Selling price
3. Selling Price = Commission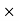 100/ Commission %
100/ Commission %
4. Commission (Brokerage) = Commission%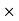 Selling price/100
Selling price/100