Unit-2
Bearing capacity of shallow foundation
METHODS OF DETERMINING BEARING CAPACITY
Key takeaways
Bearing capacity tables in numerous building codes
Analytical methods
Plate bearing tests
Penetration tests
Model tests and model tests
Laboratory tests
VARIOUS TERMS RELATED TO BEARING CAPACITY
Various terms involving bearing capability
Ultimate bearing capacity (UBC)
DEFINITION- it's outlined because the minimum gross pressure intensity at the bottom of the muse at that the soil fails in sheer
Net bearing capacity (NBC),
In the ultimate B.C. (UBC) - surcharge result
q u n = q u –q
q u n = c N C + q (N q -1 ) + 0.5 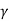 BN q
BN q
Safe Bearing capacity (SBC),
SBC for footing placed at depth Dr
q F = q u n /F s+ 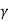 Df
Df
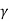
q f = q u n / Fs
Safe soil pressure, q f = q u n /Fs +  D f
D f
Unit soil pressure
Allowable soil pressure
Key takeaways
The following are some important ones
1 Type of soil
2 Unit weight of soil
3. Surcharge load
4. Depth of foundation
5. Mode of failure
6 Size of footing
7. Form of footing
8. Depth of geological formation
9. Eccentricity in footing loud
10. Inclination of footing load
11. Inclination of ground
12 Inclination of the base of the foundation
The factor of Safety (F)
It's the factor of content regarding the soil beneath consideration. It depends on several factors appreciate
Shear failure of soil under foundation base San takes place in three different ways depending on the type of soil pattern and location of the foundation.
Modes of failure
1. General shear failure
2. Local shear failure
3. Punching shear failure
1. GENERAL SHEAR FAILURE
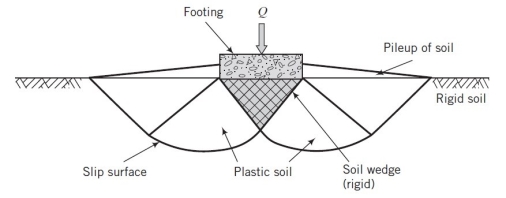
Fig no. 1 General shear failure
2. LOCAL SHEAR FAILURE
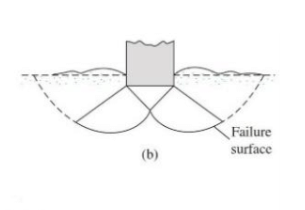
Fig no. 2 Local shear failure
3 PUNCHING SHEAR FAILURE
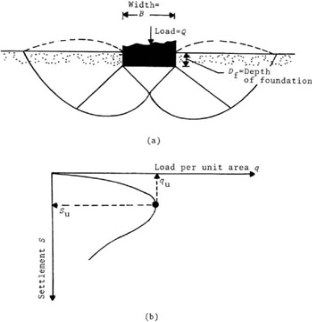
Fig no. 3 Punching shear failure
Key takeaways
1. General shear failure
2. Local shear failure
3. Punching shear failure
Depend upon the ratio of D (depth) and W (width) foundation is classified as under
1. Shallow foundation = D/W >1
2. Deep foundation = D/W <1
Type of shallow foundation
A shallow foundation is classified according to the distribution of load on the soil as shown below
2. Cantilever strap or pump handle footing
3. Raft footing
2. Sloped footing
3. Grillage footing
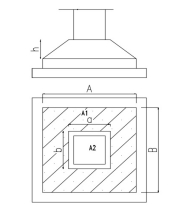
Fig no 4 Fig no 5
Trapezoidal footing Combined footing
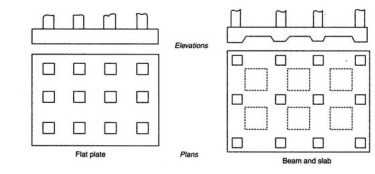
Fig no 6 Mat foundation
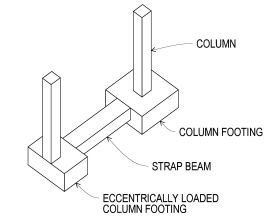
Fig no7 Strap footing
SPREAD FOOTING
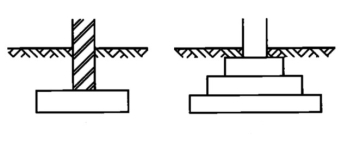
Fig no 8 Spread footing
1. If the projection of footing on the far side wall is excessive, the footing could crack thanks to soil reaction within the cantilever portion. Hence, the stepped foundation is provided.
2 If thickness "t" of footing is a smaller amount, the wall could clock in the footing.
3. Depth of foundation (D) ought to be adequate offer necessary safe bearing capability. Minimum depth of the foundation of ninety cm is provided
MAT OR RAFT FOUNDATION
Types of mat foundation
1. Flat plate met
2. Plate thickened under the column
3. Plate with pedestal
4. Piled raft
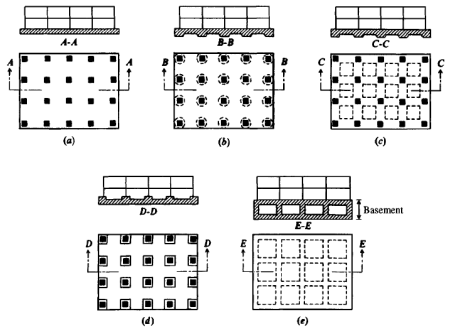
Fig no 9 Types of mat foundation
(a) Flat plate mat
It is appropriate for fewer compressible soil and comparatively lightweight hundreds with nearer and uniform column spacing
(b) Pate thickened below columns
It is appropriate for heavily loaded columns and provides safety from diagonal shear and negative moments
(c) Plate with pedestal
Pedestals square measure provided at the base of columns higher than slab associated serve the same purpose as kind (b)
(d) Piled raft
When soil is incredibly compressible and geological formation is high, this ruft reduces the settlement and might management buoyancy.
Key takeaways
The pressure transmitted from the bottom of a foundation to the soil is termed the contact pressure.
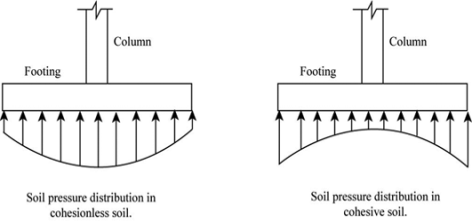
Fig no 10 Flexible and soil footing on cohesive soil
Terzaghi’s analysis although not rigorous permits the USA to work out the final bearing capability of shallow strip footing with a rough base.
Assumptions concerned within the Terzaghi theory
1 The footing is rough (This is a common actual field condition)
2. It is shallow i.e. its depth below the surface isn't greater than the dimension.
3. The shear strength of the soil between the bottom level and also the bottom footing is neglected and this soil is taken into account solely as a surcharge imposing uniform pressure on the horizontal plane at foundation level.
4. General shear failure is assumed which the degree of the soil before and when failure is unchanged.
5. A wedge of soil forthwith below the bottom in a state of elastic equilibrium LE. it's half and parcel of the footing.
6. Passive pressure Pp consists of 3 parts which might be calculated on an individual basis and intercalary though the essential surfaces for these parts aren't identical.
7. Failure zones don't extend on top of the horizontal plane through the bottom of the footing i.e. the shear resistance of soil on top of the bottom is neglected and also the impact of soil around the footing is taken into account akin to a surcharge q=YD.
8. The footing is continuous. This makes the matter a two dimensional one. For isolated footings, however, Terzaghi's future counseled some correction factors to be applied to tie bearing capability values figured out for continuous footing.
Based on these assumptions, the last word bearing capability ratio is figured out as mentioned below:
Derivation of equation for bearing capacity
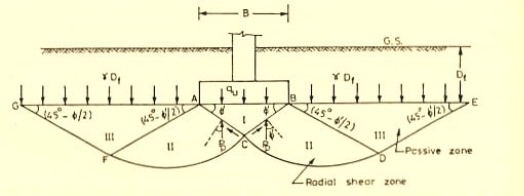
Fig no. 11 Terzaghis equation
The forces functioning on these planes
1. Cohesion c acting on the surfaces CB and CA
2. The resultant of passive pressure Pp. creating associate angle o with the traditional to the surfaces CB and CA. Now, whenthe surface AC associated BC build an angle o with the horizontal, then the passive pressure P would act vertically upward. At failure, the downward and therefore the upward forces on the wedge ACB of unit length should be equal. Additionally, during this position, the building load alphabetic character can represent the final word bearing capability of the soil, and therefore may be substituted by q u r. Hence, the downward forces per m run.
1. qu l t
2. The load of the wedge ACB =1/2 B (height of 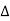 )
)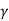 = ½ B B/2
= ½ B B/2
3. Tan 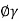 = ¼
= ¼ 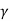 B2 tan
B2 tan 
The upward forces are: (1) the passive pressures Pp on every of the surface AC and BC i.e. 2 Pp: and (2) the upward element of cohesion is, acting on CA and CB
= 2 CA c sin  = 2 ((B/2)/ Cos
= 2 ((B/2)/ Cos ) c sin
) c sin  = Bc tan
= Bc tan 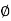
Equating downward and upward forces, we get
q u l t .B + ¼ 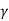 B2 Tan
B2 Tan 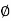 = 2 Pp + B .c tan
= 2 Pp + B .c tan 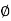
q u l t B = 2 Pp + bc tan 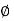 - ¼
- ¼ 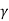 B2 tan
B2 tan 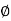
The total passive pressure Pp encompass the subsequent
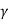
q u l t B = 2 [Pp(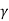 ) + Pp(c) + Pp(q)] + Bc tan
) + Pp(c) + Pp(q)] + Bc tan 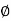 - ¼
- ¼ 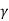 B2tan
B2tan 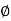
Since the term (2 Pp(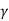 ) – ¼
) – ¼ 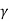 B2 tan
B2 tan  ) depends on
) depends on 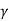
Let us express it as N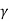 .
.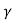 B2
B2
2 Pp (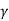 ) – ¼
) – ¼ 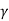 B2 tan
B2 tan 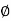 = (N
= (N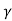 )
) 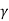 B2/2
B2/2
2 P p(c) + Bc tan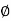 = N c Bc
= N c Bc
2 Pp(q) = N q B 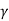 Df
Df
Where N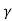 , Nc and N q are dimensionless bearing capability factors, counting on The Equation then becomes:
, Nc and N q are dimensionless bearing capability factors, counting on The Equation then becomes:
C= cohesion
D = depth of the foundation
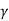 = unit weight of soil
= unit weight of soil
Terzaghi gave the subsequent expression for the bearing capability face
N q = 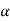 2 / [2 Cos 2 (45+
2 / [2 Cos 2 (45+ 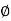 /2)]
/2)]
N c = (N q-1) cot 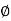
And
N 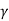 = tan
= tan 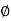 /2 [(K p y /cos2
/2 [(K p y /cos2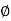 )-1]
)-1]
Kp 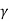 = Passive earth pressure constant depends upon
= Passive earth pressure constant depends upon 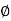
The values of N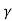 at
at 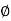 = 0, 34, 45, are 0, 35, 297.5
= 0, 34, 45, are 0, 35, 297.5
Limitations of Terzaghi's Theory
2 Error thanks to the assumption that P, consists of 3 parts, which might be calculated severally and supplementary is little and on the safe aspect.
3 Error thanks to the assumption that failure zones don't extend on top of the horizontal plane through the base of footing and surcharge load. q = y D, isn't true as a result of surcharge load will increase with depth of foundation and thus the speculation is appropriate for shallow foundation only
Key takeaways
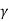
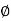
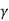
It differs from Terzaghi's equation as
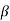
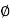
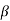 =45+
=45+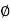 /2
/2
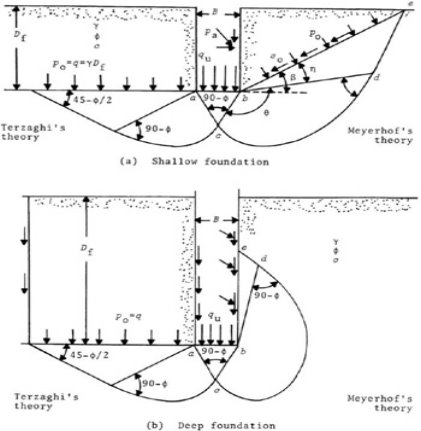
Fig no. 12 Meyerhofs analysis
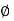
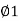
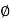
q u = c N c s c dc Ic + q N q S q d q I q + 0.5 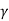 B N
B N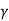 s
s 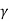 d
d 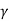 I
I 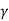
And is in shut agreement with the expected result for cohesive soil
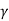
Here N q = tan 2 [(45 +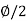 )] e
)] e 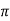 tan
tan 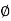
N c = (N q -1) cot 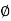
N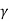 = 1.8 (Nq-1) tan
= 1.8 (Nq-1) tan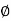
Vesic Analysis: it's just like Hansen's equation only there's a slight distinction in the worth of N, and variation on some of Hansen's inclination, form and depth factors.
Vesic's formula for N 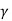 states
states
N 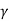 = 2 (N c +1) tan
= 2 (N c +1) tan 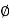
Hansen's and Vesic's bearing capability factors area unit satisfactory for non-cohesive likewise as cohesive soils.
| Nc | Nq | Ny | Ny (verses) |
0 | 5.14 | 1 | 0.0 | - |
5 | 6.48 | 1.57 | 0.09 | 0.45 |
10 | 8.34 | 2.47 | 0.47 | 1.22 |
15 | 10.97 | 3.94 | 1.42 | 2.65 |
20 | 14.83 | 6.4 | 3.54 | 5.39 |
25 | 20.72 | 10.66 | 8.11 | 10.88 |
30 | 30.14 | 18.4 | 18.08 | 22.4 |
35 | 46.13 | 33.29 | 40.69 | 48.03 |
40 | 75.32 | 64.18 | 95.41 | 109.41 |
45 | 133.89 | 134.85 | 240.85 | 271.76 |
50 | 266.89 | 318.96 | 681.84 | 762.89 |
B = form issue to account for the impact of the form of foundation in developing failure surface.
d = Depth issue to account for embedment depth and therefore the further cut resistance within the prime soil
i = Inclination issue to account for each horizontal and vertical part of foundation hundreds.
S FACTOR
|
| Sc | Sq | Sf |
A | Strips | 1 | 1 | 1 |
B | Rectangular | 1 + 0.2 B/L | 1 + 0.2 B/L | 1- 0.4 B/L |
C | Square | 1.3 | 1.2 | 0.8 |
D | Circle | 1.3 | 1.2 | 0.6 |
d FACTOR
d c = 1+ 0.2 ∆f/B (√N Q )
d q = 1 for 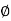 < 10
< 10
d q = 1+ 0.1 ∆f/B (√NQ )
Where
NQ = tan² ( 45+ 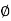 /2 )
/2 )
I -FACTOR
I c = (1- 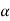 /
/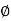 )2
)2
Key takeaways
Bearing capacity by Hansen analysis
q u = c N c s c d c I c + q N q S q d q I q + 0.5 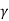 B N
B N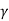 s
s 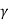 d
d 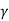 I
I 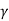
Here
N q = tan 2 [(45 +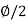 )] e
)] e 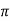 tan
tan 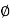
N c = (N q -1) cot 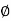
N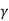 = 1.8 (Nq-1) tan
= 1.8 (Nq-1) tan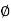
The ultimate net bearing capacity of strip footing is given by the following equation
For the case of general shear failure
q nf = c Nc + q (Nq -1) + 1/2 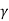 B N
B N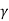
For the case of local shear failure
qnf =2/3 c N c’ + q (Nq’ -1) + 1/2 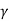 B N
B N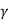
Where
q = effective surcharge at the base level of foundation
Nc , Nq , Nf = bearing capacity factors
1. Lowering of geological formation and dewatering may end up in shrinkage of soil and increment of stresses in soil.
2. Static countless foundations will cause elastic compression or plastic flow in a static short amount of your time and may result in consolidation settlement over a protracted amount of your time.
3. Dynamic loading will cause shocks and vibrations leading to compaction of soil and in fine saturated sands and silts, physical change might occur throughout earthquakes.
4. Throughout major construction activities in close areas like deep excavations, pile driving, mining activities or heavily loaded structures may lead to a settlement.
5. Other causes like the collapse of pipe conduits, erosion of undersoil, or submersion resulting in the collapse of soil structures may cause settlement of foundations
ALLOWABLE SETTLEMENT
Basically, the settlement has 2 types
Differential settlement
Immediate settlement
While analyzing the settlement of foundation 2 aspects are needed to be studied:
As way as the time needed to achieve total settlement is can depend
The settlement is a combination of 2 parts
As way as compression for soil and compression of water thinks about, it's negligible. Thus, the reduction in the volume of a saturated soil sample is especially thanks to the escape of water.
In the case of part saturated soil, there'll not be any flow of water, however, because of compressible air, there'll be a considerable reduction in volume.
In the gift study, time-dependent compression of partially saturated soil is on the far side of the scope of this book, and only time-dependent compression just in case of saturated soil is taken into account
Once the load is applied on saturated cohesive soil, initially, the entire load is taken by pore water, and later on, because of gradual escape/seepage of water, the load is transferred to the soil.
The settlement because of consolidation will be divided into 2 elements
Types of settlement
Primary consolidation settlement
Secondary consolidation settlement
Primary consolidation settlement (Sc) is that the settlement resulted because of resistance to the flow of water beneath the evoked hydraulic gradient.
Secondary consolidation settlement (S s) is because of plastic deformation of soil at zero excess pore water pressure
Mathematically S = total settlement = SI +Sc +Ss
If the load is applied on saturated non-cohesive soil, where drainage is not permitted, less compression/settlement will take for the following reasons:
Water is highly incompressible
Modulus of chastity of sand is less
Key takeaways
For settlement, there are 2 aspects
Consolidation - Definition -This method of gradual load transfer from pore water to soil Skeleton, and gradual compression is termed consolidation
Settlement because of consolidation
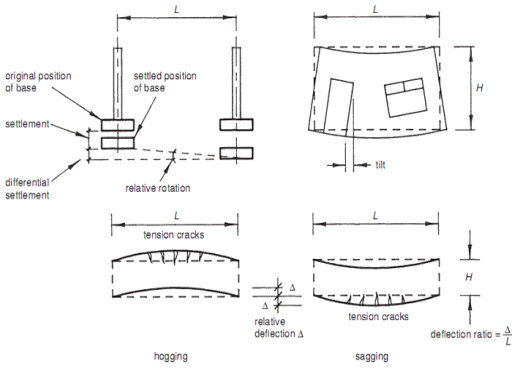
Fig no. 13 Differential settlements
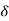
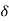
Then differential settlement = 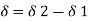
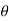 =
= 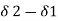 / l =
/ l = 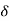 /l
/l
This angular distortion causes a lot of injury to the structure.
(A) Causes of differential settlement
(B) Methods to reduce differential settlement
IMMEDIATE SETTLEMENT
S I = 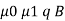 [(1-
[(1- 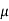 2)/E s]
2)/E s]
Where the modulus of clay town E s is computed from
Es = (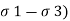 / (
/ (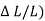
And 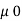 and
and 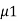 taken from the graph
taken from the graph
When completely different clay layers exist, having completely different values of E, by victimization the principle of superposition computations may be plane. This price of S, once accessorial to S, would offer the whole settlement for such soils.
S I = q B [(1- 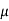 2) I w / E s]
2) I w / E s]
Where
q = Intensity of contact pressure
B = Least lateral dimension of footing
E s = Modulus of the physical property of soil
I w = Influence issue
= 0.88 for rigid circular footing
= 0.82 for rigid sq. footing
= 1.06 for rigid rectangular footing with L/B
= 1.5
= 1.70 for rigid rectangular footing, with LSB
= 5
The values of influence clotting factor area unit urged in IS code I S: 8009 half I, 1976. Per this code, the entire settlement of a rigid footing is taken as zero.8 times the settlement at the middle of a versatile foundation,
This equation is base on the belief that the load is performing at ground level i.e. impact of depth of footing below GL and depth of exhausting strata below footing isn't thought-about. This can be taken under consideration within the equation explicit in the previous paragraph.
Key takeaways
Differential settlement is given by
Differential settlement = 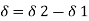
Angular distortion = differential settlements / distance between 2 column
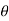 =
= 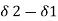 / l =
/ l = 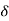 /l
/l
Immediate settlement
S I = q B [(1- 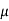 2) I w / E s]
2) I w / E s]
Where the modulus of clay town E s is computed from
Es = (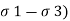 / (
/ (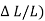
References
1. Arora K R: soil mechanics and foundation engg Delhi
2. B.C. Punamia : soil mechanics and foundation engg; Laxmi publication Delhi
3. Gulati S.K: geotechnical engineering Hill education Pvt limited, Noida