Unit – 2
Arithmetic and logic unit
In case of parallel adders, the binary addition of two numbers is initiated when all the bits of the augend and the addend must be available at the same time to perform the computation. In a parallel adder circuit, the carry output of each full adder stage is connected to the carry input of the next higher-order stage, hence it is also called as ripple carry type adder.
In such adder circuits, it is not possible to produce the sum and carry outputs of any stage until the input carry occurs. So there will be a considerable time delay in the addition process, which is known as, carry propagation delay. In any combinational circuit, signal must propagate through the gates before the correct output sum is available in the output terminals.
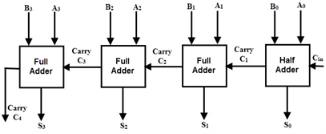
Fig - Example
Consider the above figure, in which the sum S4 is produced by the corresponding full adder as soon as the input signals are applied to it. But the carry input C4 is not available on its final steady state value until carry c3 is available at its steady state value. Similarly, C3 depends on C2 and C2 on C1. Therefore, carry must propagate to all the stages in order that output S4 and carry C5 settle their final steady-state value.
The propagation time is equal to the propagation delay of the typical gate times the number of gate levels in the circuit. For example, if each full adder stage has a propagation delay of 20n seconds, then S4 will reach its final correct value after 80n (20 × 4) seconds. If we extend the number of stages for adding a greater number of bits then this situation becomes much worse.
So the speed at which the number of bits added in the parallel adder depends on the carry propagation time. However, signals must be propagated through the gates at a given enough time to produce the correct or desired output.
The following are the methods to get the high speed in the parallel adder to produce the binary addition.
- By employing faster gates with reduced delays, we can reduce the propagation delay. But there will be a capability limit for every physical logic gate.
- Another way is to increase the circuit complexity in order to reduce the carry delay time. There are several methods available to speeding up the parallel adder, one commonly used method employs the principle of look ahead-carry addition by eliminating inter stage carry logic.
Carry-Lookahead Adder
A carry-Lookahead adder is a fast parallel adder as it reduces the propagation delay by more complex hardware, hence it is costlier. In this design, the carry logic over fixed groups of bits of the adder is reduced to two-level logic, which is nothing but a transformation of the ripple carry design.
This method makes use of logic gates so as to look at the lower order bits of the augend and addend to see whether a higher order carry is to be generated or not. Let us discuss in detail.
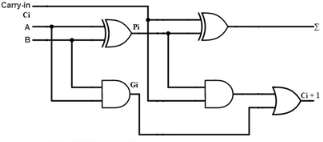
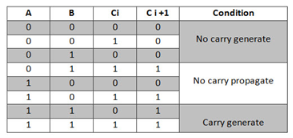
Fig- Example
Consider the full adder circuit shown above with corresponding truth table. If we define two variables as carry generate Gi and carry propagate Pi then,
Pi = Ai⊕ Bi
Gi = Ai Bi
The sum output and carry output can be expressed as
Si = Pi ⊕ Ci
C i +1 = Gi + Pi Ci
Where Gi is a carry generate which produces the carry when both Ai, Bi are one regardless of the input carry. Pi is a carry propagate and it is associate with the propagation of carry from Ci to Ci +1.
The carry output Boolean function of each stage in a 4 stage carry-Lookahead adder can be expressed as
C1 = G0 + P0 Cin
C2 = G1 + P1 C1
= G1 + P1 G0 + P1 P0 Cin
C3 = G2 + P2 C2
= G2 + P2 G1+ P2 P1 G0 + P2 P1 P0 Cin
C4 = G3 + P3 C3
= G3 + P3 G2+ P3 P2 G1 + P3 P2 P1 G0 + P3 P2 P1 P0 Cin
From the above Boolean equations, we can observe that C4 does not have to wait for C3 and C2 to propagate but actually C4 is propagated at the same time as C3 and C2. Since the Boolean expression for each carry output is the sum of products so these can be implemented with one level of AND gates followed by an OR gate.
The implementation of three Boolean functions for each carry output (C2, C3 and C4) for a carry-Lookahead carry generator shown in below figure.
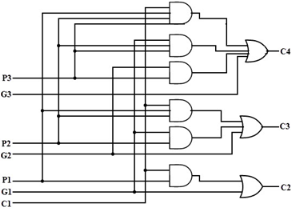
Fig 28 – Look ahead carry generator
Therefore, a 4-bit parallel adder can be implemented with the carry-Lookahead scheme to increase the speed of binary addition as shown in below figure. In this, two Ex-OR gates are required by each sum output. The first Ex-OR gate generates Pi variable output and the AND gate generates Gi variable.
Hence, in two gates levels all these P’s and G’s are generated. The carry-Lookahead generators allows all these P and G signals to propagate after they settle into their steady state values and produces the output carriers at a delay of two levels of gates. Therefore, the sum outputs S2 to S4 have equal propagation delay times.
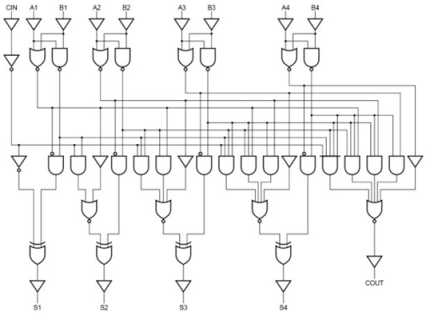
Fig 29 - example
It is also possible to construct 16 bit and 32-bit parallel adders by cascading the number of 4-bit adders with carry logic. A 16 bit carry-Lookahead adder is constructed by cascading the four 4-bit adders with two more gate delays, whereas the 32 bit carry-Lookahead adder is formed by cascading of two 16 bit adders.
In a 16 bit carry-Lookahead adder, 5 and 8 gate delays are required to get C16 and S15 respectively, which are less as compared to the 9 and 10 gate delay for C16 and S15 respectively in cascaded four bit carry-Lookahead adder blocks. Similarly, in 32-bit adder, 7 and 10 gate delays are required by C32 and S31 which are less compared to 18 and 17 gate delays for the same outputs if the 32-bit adder is implemented by eight 4 bit adders.
Carry-Lookahead Adder ICs
The high-speed carry-Lookahead adders are integrated on integrated circuits in different bit configurations by several manufacturers. There are several individual carry generator ICs are available so that we have to make connection with logic gates to perform the addition operation.
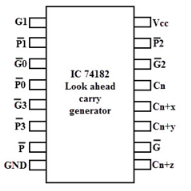
A typical carry-Lookahead generator IC is 74182 which accept four pairs of active low carry propagate (as P0, P1, P2 and P3) and carry generate (Go, G1, G2 and G3) signals and an active high input (Cn).
It provides active high carriers (Cn+x, Cn+y, Cn+z) across the four groups of binary adders. This IC also facilitates the other levels of look ahead by active low propagate and carry generate outputs.
The logic expressions provided by the IC 74182 are
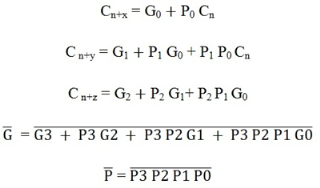
On the other hand, there are many high-speed adder ICs which combine a set of full adders with carry-Lookahead circuitry. The most popular form of such IC is 74LS83/74S283 which is a 4-bit parallel adder high speed IC that contains four interconnected full adders with a carry-Lookahead circuitry.
The functional symbol for this type of IC is shown in below figure. It accepts the two 4 bit numbers as A3A2A1A0 and B3B2B1B0 and input carry Cin0 into the LSB position. This IC produce output sum bits as S3S2S1S0 and the carry output Cout3 into the MSB position.
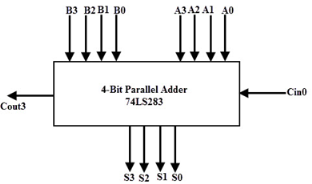
By cascading two or more parallel adder ICs we can perform the addition of larger binary numbers such as 8 bit, 24-bit and 32 bit addition.
Key takeaway
In case of parallel adders, the binary addition of two numbers is initiated when all the bits of the augend and the addend must be available at the same time to perform the computation. In a parallel adder circuit, the carry output of each full adder stage is connected to the carry input of the next higher-order stage, hence it is also called as ripple carry type adder.
In such adder circuits, it is not possible to produce the sum and carry outputs of any stage until the input carry occurs. So there will be a considerable time delay in the addition process, which is known as, carry propagation delay. In any combinational circuit, signal must propagate through the gates before the correct output sum is available in the output terminals.
Multiplication of two fixed point binary number in signed magnitude representation is done with process of successive shift and add operation.

In the multiplication process we are considering successive bits of the multiplier, least significant bit first.
If the multiplier bit is 1, the multiplicand is copied down else 0’s are copied down.
The numbers copied down in successive lines are shifted one position to the left from the previous number.
Finally numbers are added and their sum form the product.
The sign of the product is determined from the sign of the multiplicand and multiplier. If they are alike, sign of the product is positive else negative.
Hardware Implementation:
Following components are required for the Hardware Implementation of multiplication algorithm:
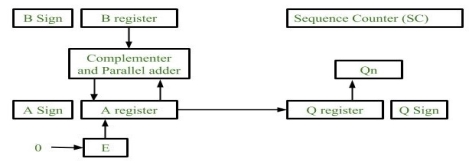
Fig – Hardware Implementation
- Registers:
Two Registers B and Q are used to store multiplicand and multiplier respectively.
Register A is used to store partial product during multiplication.
Sequence Counter register (SC) is used to store number of bits in the multiplier. - Flip Flop:
To store sign bit of registers we require three flip flops (A sign, B sign and Q sign).
Flip flop E is used to store carry bit generated during partial product addition. - Complement and Parallel adder:
This hardware unit is used in calculating partial product i.e, perform addition required.
Flowchart of Multiplication:
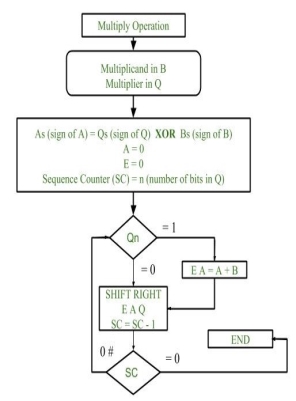
Fig 9 – Flowchart of Multiplication
- Initially multiplicand is stored in B register and multiplier is stored in Q register.
- Sign of registers B (Bs) and Q (Qs) are compared using XOR functionality (i.e., if both the signs are alike, output of XOR operation is 0 unless 1) and output stored in As (sign of A register).
Note: Initially 0 is assigned to register A and E flip flop. Sequence counter is initialized with value n, n is the number of bits in the Multiplier.
3. Now least significant bit of multiplier is checked. If it is 1 add the content of register A with Multiplicand (register B) and result is assigned in A register with carry bit in flip flop E. Content of E A Q is shifted to right by one position, i.e., content of E is shifted to most significant bit (MSB) of A and least significant bit of A is shifted to most significant bit of Q.
4. If Qn = 0, only shift right operation on content of E A Q is performed in a similar fashion.
5. Content of Sequence counter is decremented by 1.
6. Check the content of Sequence counter (SC), if it is 0, end the process and the final product is present in register A and Q, else repeat the process.
Example:
Multiplicand = 10111
Multiplier = 10011
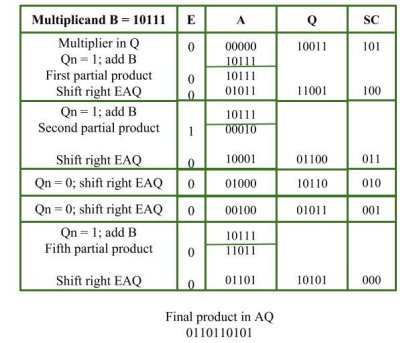
Key takeaway
Multiplication of two fixed point binary number in signed magnitude representation is done with process of successive shift and add operation.

In the multiplication process we are considering successive bits of the multiplier, least significant bit first.
If the multiplier bit is 1, the multiplicand is copied down else 0’s are copied down.
The numbers copied down in successive lines are shifted one position to the left from the previous number.
Finally numbers are added and their sum form the product.
The sign of the product is determined from the sign of the multiplicand and multiplier. If they are alike, sign of the product is positive else negative
Booths algorithm
The booth algorithm is a multiplication algorithm that allows us to multiply the two signed binary integers in 2's complement, respectively. It is also used to speed up the performance of the multiplication process. It is very efficient too. It works on the string bits 0's in the multiplier that requires no additional bit only shift the right-most string bits and a string of 1's in a multiplier bit weight 2k to weight 2m that can be considered as 2k+ 1 - 2m.
Following is the pictorial representation of the Booth's Algorithm:
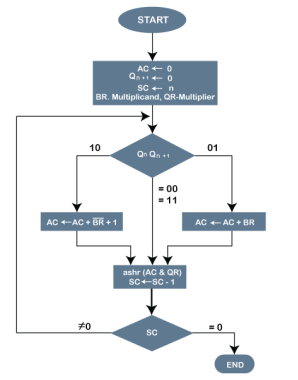
Fig 10 - Pictorial representation of the Booth's Algorithm
In the above flowchart, initially, AC and Qn + 1 bits are set to 0, and the SC is a sequence counter that represents the total bits set n, which is equal to the number of bits in the multiplier. There are BR that represent the multiplicand bits, and QR represents the multiplier bits. After that, we encountered two bits of the multiplier as Qn and Qn + 1, where Qn represents the last bit of QR, and Qn + 1 represents the incremented bit of Qn by 1. Suppose two bits of the multiplier is equal to 10; it means that we have to subtract the multiplier from the partial product in the accumulator AC and then perform the arithmetic shift operation (ashr). If the two of the multipliers equal to 01, it means we need to perform the addition of the multiplicand to the partial product in accumulator AC and then perform the arithmetic shift operation (ashr), including Qn + 1. The arithmetic shift operation is used in Booth's algorithm to shift AC and QR bits to the right by one and remains the sign bit in AC unchanged. And the sequence counter is continuously decremented till the computational loop is repeated, equal to the number of bits (n).
Working on the Booth Algorithm
- Set the Multiplicand and Multiplier binary bits as M and Q, respectively.
- Initially, we set the AC and Qn + 1 registers value to 0.
- SC represents the number of Multiplier bits (Q), and it is a sequence counter that is continuously decremented till equal to the number of bits (n) or reached to 0.
- A Qn represents the last bit of the Q, and the Qn+1 shows the incremented bit of Qn by 1.
- On each cycle of the booth algorithm, Qn and Qn + 1 bits will be checked on the following parameters as follows:
- When two bits Qn and Qn + 1 are 00 or 11, we simply perform the arithmetic shift right operation (ashr) to the partial product AC. And the bits of Qn and Qn + 1 is incremented by 1 bit.
- If the bits of Qn and Qn + 1 is shows to 01, the multiplicand bits (M) will be added to the AC (Accumulator register). After that, we perform the right shift operation to the AC and QR bits by 1.
- If the bits of Qn and Qn + 1 is shows to 10, the multiplicand bits (M) will be subtracted from the AC (Accumulator register). After that, we perform the right shift operation to the AC and QR bits by 1.
- The operation continuously works till we reached n - 1 bit in the booth algorithm.
- Results of the Multiplication binary bits will be stored in the AC and QR registers.
There are two methods used in Booth's Algorithm:
1. RSC (Right Shift Circular)
It shifts the right-most bit of the binary number, and then it is added to the beginning of the binary bits.
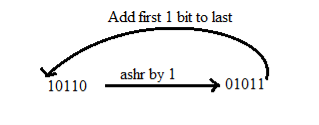
2. RSA (Right Shift Arithmetic)
It adds the two binary bits and then shift the result to the right by 1-bit position.
Example: 0100 + 0110 => 1010, after adding the binary number shift each bit by 1 to the right and put the first bit of resultant to the beginning of the new bit.
Example: Multiply the two numbers 7 and 3 by using the Booth's multiplication algorithm.
Ans. Here we have two numbers, 7 and 3. First of all, we need to convert 7 and 3 into binary numbers like 7 = (0111) and 3 = (0011). Now set 7 (in binary 0111) as multiplicand (M) and 3 (in binary 0011) as a multiplier (Q). And SC (Sequence Count) represents the number of bits, and here we have 4 bits, so set the SC = 4. Also, it shows the number of iteration cycles of the booth's algorithms and then cycles run SC = SC - 1 time.
Qn | Qn + 1 | M = (0111) | AC | Q | Qn + 1 | SC |
1 | 0 | Initial | 0000 | 0011 | 0 | 4 |
|
| Subtract (M' + 1) | 1001 |
|
|
|
|
|
| 1001 |
|
|
|
|
| Perform Arithmetic Right Shift operations (ashr) | 1100 | 1001 | 1 | 3 |
1 | 1 | Perform Arithmetic Right Shift operations (ashr) | 1110 | 0100 | 1 | 2 |
0 | 1 | Addition (A + M) | 0111 |
|
|
|
|
|
| 0101 | 0100 |
|
|
|
| Perform Arithmetic right shift operation | 0010 | 1010 | 0 | 1 |
0 | 0 | Perform Arithmetic right shift operation | 0001 | 0101 | 0 | 0 |
The numerical example of the Booth's Multiplication Algorithm is 7 x 3 = 21 and the binary representation of 21 is 10101. Here, we get the resultant in binary 00010101. Now we convert it into decimal, as (000010101)10 = 2*4 + 2*3 + 2*2 + 2*1 + 2*0 => 21.
Example: Multiply the two numbers 23 and -9 by using the Booth's multiplication algorithm.
Here, M = 23 = (010111) and Q = -9 = (110111)
Qn Qn + 1 | M = 0 1 0 1 1 1 | AC | Q | Qn + 1 SC |
| Initially | 000000 | 110111 | 0 6 |
1 0 | Subtract M | 101001 |
|
|
|
| 101001 |
|
|
| Perform Arithmetic right shift operation | 110100 | 111011 | 1 5 |
1 1 | Perform Arithmetic right shift operation | 111010 | 011101 | 1 4 |
1 1 | Perform Arithmetic right shift operation | 111101 | 001110 | 1 3 |
0 1 | Addition (A + M) | 010111 |
|
|
|
| 010100 |
|
|
| Perform Arithmetic right shift operation | 001010 | 000111 | 0 2 |
1 0 | Subtract M | 101001 |
|
|
|
| 110011 |
|
|
| Perform Arithmetic right shift operation | 111001 | 100011 | 1 1 |
1 1 | Perform Arithmetic right shift operation | 111100 | 110001 | 1 0 |
Qn + 1 = 1, it means the output is negative.
Hence, 23 * -9 = 2's complement of 111100110001 =>(00001100111)
Key takeaway
The booth algorithm is a multiplication algorithm that allows us to multiply the two signed binary integers in 2's complement, respectively. It is also used to speed up the performance of the multiplication process. It is very efficient too. It works on the string bits 0's in the multiplier that requires no additional bit only shift the right-most string bits and a string of 1's in a multiplier bit weight 2k to weight 2m that can be considered as 2k+ 1 - 2m.
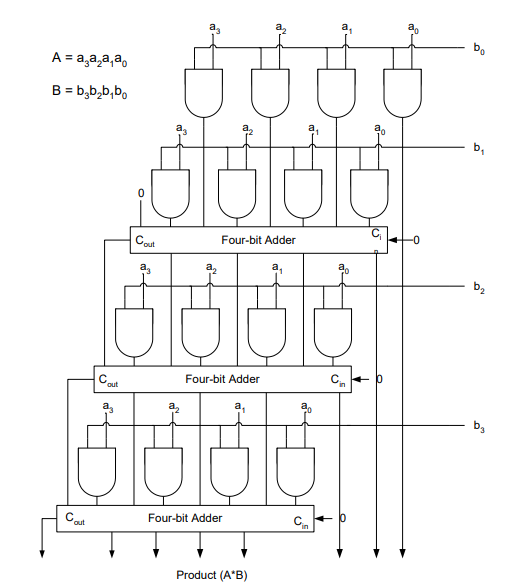
Array Multiplier
An array multiplier is a digital combinational circuit used for multiplying two binary numbers by employing an array of full adders and half adders. This array is used for the nearly simultaneous addition of the various product terms involved. To form the various product terms, an array of AND gates is used before the Adder array.
Array multiplier is well known due to its regular structure. Multiplier circuit is based on add and shift algorithm. Each partial product is generated by the multiplication of the multiplicand with one multiplier bit. The partial product are shifted according to their bit orders and then added. The addition can be performed with normal carry propagate adder. N-1 adders are required where N is the multiplier length.
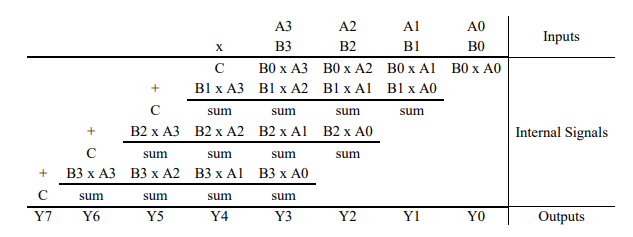
An example of 4-bit multiplication method is shown below:
A division algorithm provides a quotient and a remainder when we divide two numbers. They are generally of two type slow algorithm and fast algorithm. Slow division algorithm is restoring, non-restoring, non-performing restoring, SRT algorithm and under fast comes Newton–Raphson and Goldschmidt.
Restoring term is due to fact that value of register A is restored after each iteration.
In this example a register Q contain quotient and register A contain remainder. Here, n-bit dividend is loaded in Q and divisor is loaded in M. Value of Register is initially kept 0 and this is the register whose value is restored during iteration due to which it is named Restoring.

Following are the steps involved to perform this division
- Step-1: First the registers are initialized with corresponding values (Q = Dividend, M = Divisor, A = 0, n = number of bits in dividend)
- Step-2: Then the content of register A and Q is shifted left as if they are a single unit
- Step-3: Then content of register M is subtracted from A and result is stored in A
- Step-4: Then the most significant bit of the A is checked if it is 0 the least significant bit of Q is set to 1 otherwise if it is 1 the least significant bit of Q is set to 0 and value of register A is restored i.e. the value of A before the subtraction with M
- Step-5: The value of counter n is decremented
- Step-6: If the value of n becomes zero, we get of the loop otherwise we repeat from step 2
- Step-7: Finally, the register Q contain the quotient and A contain remainder
Examples:
Perform Division Restoring Algorithm
Dividend = 11
Divisor = 3
n | M | A | Q | Operation |
4 | 00011 | 00000 | 1011 | Initialize |
| 00011 | 00001 | 011_ | Shift left AQ |
| 00011 | 11110 | 011_ | A=A-M |
| 00011 | 00001 | 0110 | Q[0]=0 And restore A |
3 | 00011 | 00010 | 110_ | Shift left AQ |
| 00011 | 11111 | 110_ | A=A-M |
| 00011 | 00010 | 1100 | Q[0]=0 |
2 | 00011 | 00101 | 100_ | Shift left AQ |
| 00011 | 00010 | 100_ | A=A-M |
| 00011 | 00010 | 1001 | Q[0]=1 |
1 | 00011 | 00101 | 001_ | Shift left AQ |
| 00011 | 00010 | 001_ | A=A-M |
| 00011 | 00010 | 0011 | Q[0]=1 |
|
|
|
|
|
Note- Remember to restore the value of A most significant bit of A is 1. As that register Q contain the quotient, i.e. 3 and register A contain remainder 2.
A logical operation is a special symbol or word that connects two or more phrases of information. It is most often used to test whether a certain relationship between the phrases is true or false.
Some common logical gates are explained below:
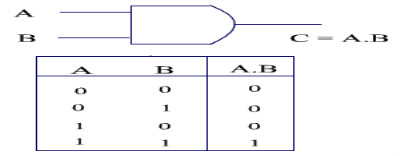
AND
The AND logic operation returns true only if either of its inputs are true. If either of the inputs is false, the output is also false.
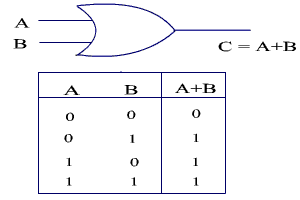
OR
The OR logic operation returns true if either of its inputs are true. If all inputs are false, the output is also false.
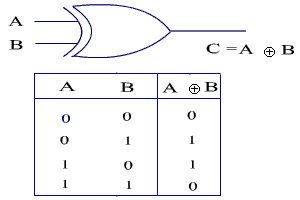
XOR
The XOR logic operation (which stands for "Exclusive OR" )returns true if either of its inputs differ, and false if they are all the same. In other words, if its inputs are a combination of true and false, the output of XOR is true. If its inputs are all true or all false, the output of XOR is false.
The objectives of this module are to discuss the need for floating point numbers, the standard representation used for floating point numbers and discuss how the various floating point arithmetic operations of addition, subtraction, multiplication and division are carried out.
Floating-point numbers and operations
Representation
When you have to represent very small or very large numbers, a fixed point representation will not do. The accuracy will be lost. Therefore, you will have to look at floating-point representations, where the binary point is assumed to be floating. When you consider a decimal number 12.34 * 107, this can also be treated as 0.1234 * 109, where 0.1234 is the fixed-point mantissa. The other part represents the exponent value, and indicates that the actual position of the binary point is 9 positions to the right (left) of the indicated binary point in the fraction. Since the binary point can be moved to any position and the exponent value adjusted appropriately, it is called a floating-point representation. By convention, you generally go in for a normalized representation, wherein the floating-point is placed to the right of the first nonzero (significant) digit. The base need not be specified explicitly and the sign, the significant digits and the signed exponent constitute the representation.
The IEEE (Institute of Electrical and Electronics Engineers) has produced a standard for floating point arithmetic. This standard specifies how single precision (32 bit) and double precision (64 bit) floating point numbers are to be represented, as well as how arithmetic should be carried out on them. The IEEE single precision floating point standard representation requires a 32 bit word, which may be represented as numbered from 0 to 31, left to right. The first bit is the sign bit, S, the next eight bits are the exponent bits, ‘E’, and the final 23 bits are the fraction ‘F’. Instead of the signed exponent E, the value stored is an unsigned integer E’ = E + 127, called the excess-127 format. Therefore, E’ is in the range 0 £ E’ £ 255.
S E’E’E’E’E’E’E’E’ FFFFFFFFFFFFFFFFFFFFFFF
0 1 8 9 31
The value V represented by the word may be determined as follows:
- If E’ = 255 and F is nonzero, then V = NaN (“Not a number”)
- If E’ = 255 and F is zero and S is 1, then V = -Infinity
- If E’ = 255 and F is zero and S is 0, then V = Infinity
- If 0 < E< 255 then V =(-1)**S * 2 ** (E-127) * (1.F) where “1.F” is intended to represent the binary number created by prefixing F with an implicit leading 1 and a binary point.
- If E’ = 0 and F is nonzero, then V = (-1)**S * 2 ** (-126) * (0.F). These are “unnormalized” values.
- If E’= 0 and F is zero and S is 1, then V = -0
- If E’ = 0 and F is zero and S is 0, then V = 0
For example,
0 00000000 00000000000000000000000 = 0
1 00000000 00000000000000000000000 = -0
0 11111111 00000000000000000000000 = Infinity
1 11111111 00000000000000000000000 = -Infinity
0 11111111 00000100000000000000000 = NaN
1 11111111 00100010001001010101010 = NaN
0 10000000 00000000000000000000000 = +1 * 2**(128-127) * 1.0 = 2
0 10000001 10100000000000000000000 = +1 * 2**(129-127) * 1.101 = 6.5
1 10000001 10100000000000000000000 = -1 * 2**(129-127) * 1.101 = -6.5
0 00000001 00000000000000000000000 = +1 * 2**(1-127) * 1.0 = 2**(-126)
0 00000000 10000000000000000000000 = +1 * 2**(-126) * 0.1 = 2**(-127)
0 00000000 00000000000000000000001 = +1 * 2**(-126) *
0.00000000000000000000001 = 2**(-149) (Smallest positive value)
(unnormalized values)
Double Precision Numbers:
The IEEE double precision floating point standard representation requires a 64-bit word, which may be represented as numbered from 0 to 63, left to right. The first bit is the sign bit, S, the next eleven bits are the excess-1023 exponent bits, E’, and the final 52 bits are the fraction ‘F’:
S E’E’E’E’E’E’E’E’E’E’E’
FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
0 1 11 12
63
The value V represented by the word may be determined as follows:
- If E’ = 2047 and F is nonzero, then V = NaN (“Not a number”)
- If E’= 2047 and F is zero and S is 1, then V = -Infinity
- If E’= 2047 and F is zero and S is 0, then V = Infinity
- If 0 < E’< 2047 then V = (-1)**S * 2 ** (E-1023) * (1.F) where “1.F” is intended to represent the binary number created by prefixing F with an implicit leading 1 and a binary point.
- If E’= 0 and F is nonzero, then V = (-1)**S * 2 ** (-1022) * (0.F) These are “unnormalized” values.
- If E’= 0 and F is zero and S is 1, then V = – 0
- If E’= 0 and F is zero and S is 0, then V = 0
Arithmetic unit
Arithmetic operations on floating point numbers consist of addition, subtraction, multiplication and division. The operations are done with algorithms similar to those used on sign magnitude integers (because of the similarity of representation) — example, only add numbers of the same sign. If the numbers are of opposite sign, must do subtraction.
ADDITION
Example on decimal value given in scientific notation:
3.25 x 10 ** 3
+ 2.63 x 10 ** -1
—————–
First step: align decimal points
Second step: add
3.25 x 10 ** 3
+ 0.000263 x 10 ** 3
——————–
3.250263 x 10 ** 3
(Presumes use of infinite precision, without regard for accuracy)
Third step: normalize the result (already normalized!)
Example on floating pt. Value given in binary:
.25 = 0 01111101 00000000000000000000000
100 = 0 10000101 10010000000000000000000
To add these fl. Pt. Representations,
Step 1: align radix points
Shifting the mantissa left by 1 bit decreases the exponent by 1
Shifting the mantissa right by 1 bit increases the exponent by 1
We want to shift the mantissa right, because the bits that fall off the end should come from the least significant end of the mantissa
-> choose to shift the .25, since we want to increase it’s exponent.
-> shift by 10000101
-01111101
———
00001000 (8) places.
0 01111101 00000000000000000000000 (original value)
0 01111110 10000000000000000000000 (shifted 1 place)
(Note that hidden bit is shifted into msb of mantissa)
0 01111111 01000000000000000000000 (shifted 2 places)
0 10000000 00100000000000000000000 (shifted 3 places)
0 10000001 00010000000000000000000 (shifted 4 places)
0 10000010 00001000000000000000000 (shifted 5 places)
0 10000011 00000100000000000000000 (shifted 6 places)
0 10000100 00000010000000000000000 (shifted 7 places)
0 10000101 00000001000000000000000 (shifted 8 places)
Step 2: add (don’t forget the hidden bit for the 100)
0 10000101 1.10010000000000000000000 (100)
+ 0 10000101 0.00000001000000000000000 (.25)
—————————————
0 10000101 1.10010001000000000000000
Step 3: normalize the result (get the “hidden bit” to be a 1)
It already is for this example.
Result is 0 10000101 10010001000000000000000
SUBTRACTION
Same as addition as far as alignment of radix points
Then the algorithm for subtraction of sign mag. Numbers takes over.
Before subtracting,
Compare magnitudes (don’t forget the hidden bit!)
Change sign bit if order of operands is changed.
Don’t forget to normalize number afterward.
MULTIPLICATION
Example on decimal values given in scientific notation:
3.0 x 10 ** 1
+ 0.5 x 10 ** 2
—————–
Algorithm: multiply mantissas
Add exponents
3.0 x 10 ** 1
+ 0.5 x 10 ** 2
—————–
1.50 x 10 ** 3
Example in binary: Consider a mantissa that is only 4 bits.
0 10000100 0100
x 1 00111100 1100

Add exponents:
Always add true exponents (otherwise the bias gets added in twice)
DIVISION
It is similar to multiplication.
Do unsigned division on the mantissas (don’t forget the hidden bit)
Subtract TRUE exponents
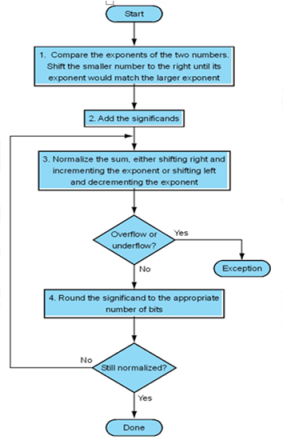
The organization of a floating point adder unit and the algorithm is given below.
The floating point multiplication algorithm is given below. A similar algorithm based on the steps discussed before can be used for division.
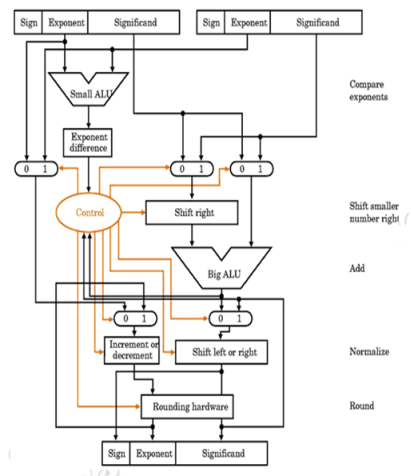
Fig – division algorithm
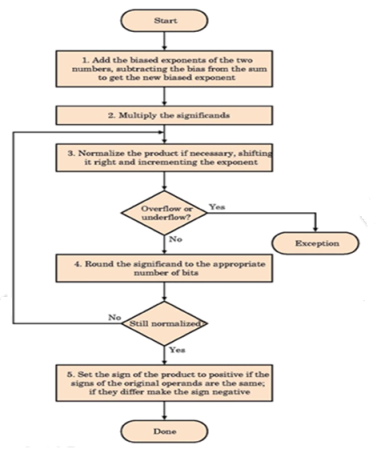
Rounding
The floating point arithmetic operations discussed above may produce a result with more digits than can be represented in 1.M. In such cases, the result must be rounded to fit into the available number of M positions. The extra bits that are used in intermediate calculations to improve the precision of the result are called guard bits. It is only a tradeoff of hardware cost (keeping extra bits) and speed versus accumulated rounding error, because finally these extra bits have to be rounded off to conform to the IEEE standard.
Rounding Methods:
- Truncate
– Remove all digits beyond those supported
– 1.00100 -> 1.00
- Round up to the next value
– 1.00100 -> 1.01
- Round down to the previous value
– 1.00100 -> 1.00
– Differs from Truncate for negative numbers
- Round-to-nearest-even
– Rounds to the even value (the one with an LSB of 0)
– 1.00100 -> 1.00
– 1.01100 -> 1.10
– Produces zero average bias
– Default mode
A product may have twice as many digits as the multiplier and multiplicand
– 1.11 x 1.01 = 10.0011
For round-to-nearest-even, we need to know the value to the right of the LSB (round bit) and whether any other digits to the right of the round digit are 1’s (the sticky bit is the OR of these digits). The IEEE standard requires the use of 3 extra bits of less significance than the 24 bits (of mantissa) implied in the single precision representation – guard bit, round bit and sticky bit. When a mantissa is to be shifted in order to align radix points, the bits that fall off the least significant end of the mantissa go into these extra bits (guard, round, and sticky bits). These bits can also be set by the normalization step in multiplication, and by extra bits of quotient (remainder) in division. The guard and round bits are just 2 extra bits of precision that are used in calculations. The sticky bit is an indication of what is/could be in lesser significant bits that are not kept. If a value of 1 ever is shifted into the sticky bit position, that sticky bit remains a 1 (“sticks” at 1), despite further shifts.
To summarize, in his module we have discussed the need for floating point numbers, the IEEE standard for representing floating point numbers, Floating point addition / subtraction, multiplication, division and the various rounding methods.
Key takeaway
The objectives of this module are to discuss the need for floating point numbers, the standard representation used for floating point numbers and discuss how the various floating point arithmetic operations of addition, subtraction, multiplication and division are carried out.
The Arithmetic Logic Unit (ALU) is the heart of any CPU. An ALU performs three kinds of operations.
- Arithmetic operations such as Addition/Subtraction,
- Logical operations such as AND, OR, etc. and
- Data movement operations such as Load and Store
ALU derives its name because it performs arithmetic and logical operations. A simple ALU design is constructed with Combinational circuits. ALUs that perform multiplication and division are designed around the circuits developed for these operations while implementing the desired algorithm. More complex ALUs are designed for executing Floating point, Decimal operations and other complex numerical operations. These are called Coprocessors and work in tandem with the main processor.
The design specifications of ALU are derived from the Instruction Set Architecture. The ALU must have the capability to execute the instructions of ISA. An instruction execution in a CPU is achieved by the movement of data/datum associated with the instruction. This movement of data is facilitated by the Datapath. For example, a LOAD instruction brings data from memory location and writes onto a GPR. The navigation of data over datapath enables the execution of LOAD instruction. We discuss Datapath more in details in the next chapter on Control Unit Design. The trade-off in ALU design is necessitated by the factors like Speed of execution, hardware cost, the width of the ALU.
Combinational ALU
A primitive ALU supporting three functions AND, OR and ADD is explained in figure below. The ALU has two inputs A and B. These inputs are fed to AND gate, OR Gate and Full ADDER. The Full Adder also has CARRY IN as an input. The combinational logic output of A and B is statically available at the output of AND, OR and Full Adder. The desired output is chosen by the Select function, which in turn is decoded from the instruction under execution. Multiplexer passes one of the inputs as output based on this select function. Select Function essentially reflects the operation to be carried out on the operands A and B. Thus A and B, A or B and A+B functions are supported by this ALU. When ALU is to be extended for more bits the logic is duplicated for as many bits and necessary cascading is done. The AND and OR logic are part of the logical unit while the adder is part of the arithmetic unit.
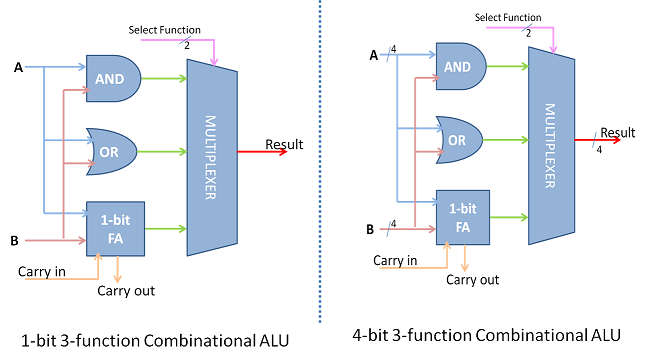
Fig- A Primitive ALU supporting AND, OR and ADD function
The simplest ALU has more functions that are essential to support the ISA of the CPU. Therefore the ALU combines the functions of 2's complement, Adder, Subtractor, as part of the arithmetic unit. The logical unit would generate logical functions of the form f(x,y) like AND, OR, NOT, XOR etc. Such a combination supplements most of a CPU's fixed point data processing instructions.
Fig- ALU Symbol
The IEEE Standard for Floating-Point Arithmetic (IEEE 754) is a technical standard for floating-point computation which was established in 1985 by the Institute of Electrical and Electronics Engineers (IEEE). The standard addressed many problems found in the diverse floating point implementations that made them difficult to use reliably and reduced their portability. IEEE Standard 754 floating point is the most common representation today for real numbers on computers, including Intel-based PC’s, Macs, and most Unix platforms.
There are several ways to represent floating point number but IEEE 754 is the most efficient in most cases. IEEE 754 has 3 basic components:
- The Sign of Mantissa –
This is as simple as the name. 0 represents a positive number while 1 represents a negative number. - The Biased exponent –
The exponent field needs to represent both positive and negative exponents. A bias is added to the actual exponent in order to get the stored exponent. - The Normalised Mantissa –
The mantissa is part of a number in scientific notation or a floating-point number, consisting of its significant digits. Here we have only 2 digits, i.e. O and 1. So a normalised mantissa is one with only one 1 to the left of the decimal.
IEEE 754 numbers are divided into two based on the above three components: single precision and double precision.
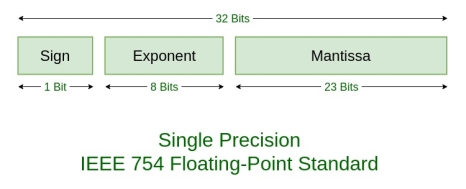
Fig– Single Precision IEEE 754 Floating Point Standard
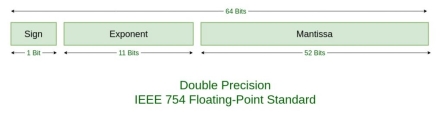
Fig – Double Precision IEEE 754 Floating point standard
TYPES | SIGN | BIASED EXPONENT | NORMALISED MANTISA | BIAS |
Single precision | 1(31st bit) | 8(30-23) | 23(22-0) | 127 |
Double precision | 1(63rd bit)
| 11(62-52) | 52(51-0) | 1023 |
Example –
85.125
85 = 1010101
0.125 = 001
85.125 = 1010101.001
=1.010101001 x 2^6
Sign = 0
1. Single precision:
Biased exponent 127+6=133
133 = 10000101
Normalised mantisa = 010101001
We will add 0's to complete the 23 bits
The IEEE 754 Single precision is:
= 0 10000101 01010100100000000000000
This can be written in hexadecimal form 42AA4000
2. Double precision:
Biased exponent 1023+6=1029
1029 = 10000000101
Normalised mantisa = 010101001
We will add 0's to complete the 52 bits
The IEEE 754 Double precision is:
= 0 10000000101 0101010010000000000000000000000000000000000000000000
This can be written in hexadecimal form 4055480000000000
Special Values: IEEE has reserved some values that can ambiguity.
- Zero –
Zero is a special value denoted with an exponent and mantissa of 0. -0 and +0 are distinct values, though they both are equal. - Denormalised –
If the exponent is all zeros, but the mantissa is not then the value is a denormalized number. This means this number does not have an assumed leading one before the binary point. - Infinity –
The values +infinity and -infinity are denoted with an exponent of all ones and a mantissa of all zeros. The sign bit distinguishes between negative infinity and positive infinity. Operations with infinite values are well defined in IEEE. - Not A Number (NAN) –
The value NAN is used to represent a value that is an error. This is represented when exponent field is all ones with a zero sign bit or a mantissa that it not 1 followed by zeros. This is a special value that might be used to denote a variable that doesn’t yet hold a value.
EXPONENT | MANTISA | VALUE |
0 | 0 | Exact 0 |
255 | 0 | Infinity |
0 | Not 0 | Denormalised |
255 | Not 0 | Not a number (NAN) |
Similar for Double precision (just replacing 255 by 2049), Ranges of Floating point numbers:
| Denormalized | Normalized | Approximate Decimal |
Single Precision | ± 2-149 to (1 – 2-23)×2-126 | ± 2-126 to (2 – 2-23)×2127 | ± approximately 10-44.85 to approximately 1038.53 |
Double Precision | ± 2-1074 to (1 – 2-52)×2-1022 | ± 2-1022 to (2 – 2-52)×21023 | ± approximately 10-323.3 to approximately 10308.3 |
The range of positive floating point numbers can be split into normalized numbers, and denormalized numbers which use only a portion of the fractions’s precision. Since every floating-point number has a corresponding, negated value, the ranges above are symmetric around zero.
There are five distinct numerical ranges that single-precision floating-point numbers are not able to represent with the scheme presented so far:
- Negative numbers less than – (2 – 2-23) × 2127 (negative overflow)
- Negative numbers greater than – 2-149 (negative underflow)
- Zero
- Positive numbers less than 2-149 (positive underflow)
- Positive numbers greater than (2 – 2-23) × 2127 (positive overflow)
Overflow generally means that values have grown too large to be represented. Underflow is a less serious problem because is just denotes a loss of precision, which is guaranteed to be closely approximated by zero.
Table of the total effective range of finite IEEE floating-point numbers is shown below:
| Binary | Decimal |
Single | ± (2 – 2-23) × 2127 | Approximately ± 1038.53 |
Double | ± (2 – 2-52) × 21023 | Approximately ± 10308.25 |
Special Operations –
Operation | Result |
n ÷ ±Infinity | 0 |
±Infinity × ±Infinity | ±Infinity |
±nonZero ÷ ±0 | ±Infinity |
±finite × ±Infinity | ±Infinity |
Infinity + Infinity | +Infinity |
-Infinity – Infinity | – Infinity |
±0 ÷ ±0 | NaN |
±Infinity ÷ ±Infinity | NaN |
±Infinity × 0 | NaN |
NaN == NaN | False |
Key takeaway
The IEEE Standard for Floating-Point Arithmetic (IEEE 754) is a technical standard for floating-point computation which was established in 1985 by the Institute of Electrical and Electronics Engineers (IEEE). The standard addressed many problems found in the diverse floating point implementations that made them difficult to use reliably and reduced their portability. IEEE Standard 754 floating point is the most common representation today for real numbers on computers, including Intel-based PC’s, Macs, and most Unix platforms.
References:
1. Computer System Architecture - M. Mano
2. Carl Hamacher, Zvonko Vranesic, Safwat Zaky Computer Organization, McGraw-Hill, Fifth Edition, Reprint 2012
3. John P. Hayes, Computer Architecture and Organization, Tata McGraw Hill, Third Edition, 1998. Reference books
4. William Stallings, Computer Organization and Architecture-Designing for Performance, Pearson Education, Seventh edition, 2006.
5. Behrooz Parahami, “Computer Architecture”, Oxford University Press, Eighth Impression, 2011.