Unit – 1

Definition of Fluid

1.1 Definition of Fluid

In simpler terms a fluid is a substance which can flow under the action of shear force (however small force may be). In physics, a fluid is a liquid or gas that continually deforms (flows) under an applied shear stress, or external force. They have zero shear modulus.

Fluids generally include liquids, gases and plasmas. To some extent, plastic solids are also considered fluids.

Example- Liquid, gases, vapour.

For a static fluid, shear force is zero.

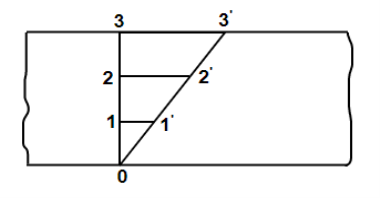
Figure: Force at static fluid

Solid regains their original shape if the shear force within elastic limit when the force is removed. But fluid never regains original shape after the removal of force.

Fluids have common properties that they share, such as compressibility, density, pressure, buoyancy and viscosity.

Fluids are basically separated in 5 types

1. Ideal fluid
2. Real fluid
3. Newtonian fluid
4. Non –Newtonian fluid
5. Ideal plastic fluid

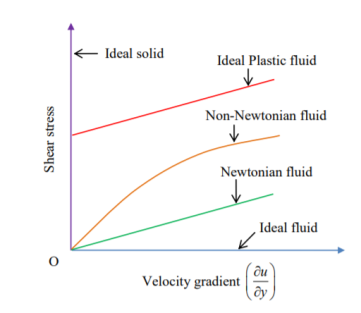
1. Ideal fluid –fluid which is incompressible in nature and no viscosity.in practical there is no ideal fluid, because all fluids have viscosity. Also called as imaginary fluid.

2. Real fluid - fluid which is compressible in nature and viscosity

Ex. Kerosene, petrol, castor oil.

3. Newtonian fluid – fluid which obeys Newton’s law of viscosity. In other words, fluids in which shear stress is directly proportional to rate of shear strain. This fluids viscosity totally depends on temperature and pressure of fluid.

Ex. Water, air, Hydrogen

4. Non –Newtonian fluid- fluid does not obey Newton’s law of viscosity. In other words, fluids in which shear stress is not directly proportional to rate of shear strain.

Ex – Flubber, Ooblek

5. Ideal plastic fluid - words fluids in which shear stress is directly proportional to rate of shear strain and in which shear stress is more than yield value.

1.2 Newton’s Law of Viscosity

The ratio of shear stress to shear rate is a constant, for a given temperature and pressure, and is defined as the viscosity or coefficient of viscosity.

According to Newton’s law of viscosity the shear stress is directly proportional to rate of shear strain or rate of angular deformation or velocity gradient. The fluid which follows this is law is called Newtonian fluid.

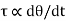
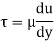
Newton’s law of viscosity is similar to Hooke’s law for solid.

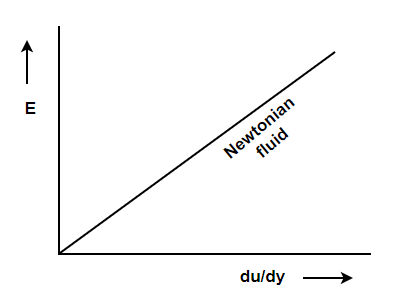
Figure: Diagram for newton’s law of viscosity

1.3 Units and Dimensions

SI units and dimension are

Quantity	Units	Dimension
Density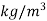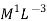
Specific weight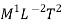
Viscosity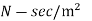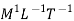
Surface tension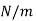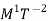

1.4 Properties of Fluids

There are various properties of fluid. Some of them are mentioned below:

1. Mass Density
2. Specific weight or weight density.
3. Specific Gravity
4. Compressibility
5. Viscosity

1.5 Mass Density

It is defined as the ratio of mass of the fluid to its volume. Its unit is     kg/m3 and its dimensional formula is ML-3.

Density depends on temperature and pressure.

1.6 Specific Volume

Specific volume is defined as the ratio of volume of fluid to the mass of fluid.

It is denoted by Vs.

Mathematically it is denoted as

Vs=V/m=1/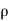

1.7 Specific Gravity

It is defined as the ratio of density of fluid to the density of standard fluid.

Or

It can be defined as the ratio of specific weight of fluid to the specific weight of standard fluid.

It is unit less or dimensionless.

For liquid, the standard fluid is water and for gases the standard fluid is either H2

Or air at given temperature and pressure.

The specific gravity of water is 1.

If the specific gravity of liquid is less than 1 that means it is lighter than water and if the specific gravity of liquid is greater than 1, it means the liquid is heavier than water.

1.8 Viscosity

It is the internal resistance offered by one layer fluid to the other layer.

Viscosity is the physic al property that characterizes the flow resistance of simple fluids.

Viscosity is the property of a fluid by virtue of its offer’s resistance to the movement of one layer of fluid over an adjacent layer.

Viscosity is also called as dynamic viscosity

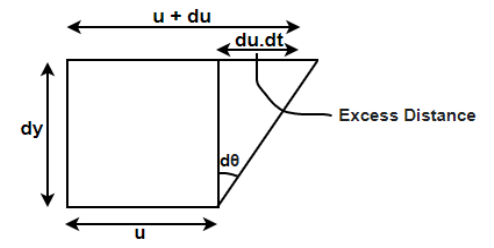
Figure: Viscosity diagram

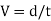
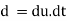
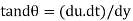
As the tandθ is very less, then

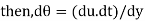
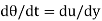
We know that, shear stress= shear force/shear area

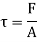
As the molecules are taken into same area:

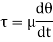
Kinematic viscosity

It is defined as the ratio of dynamic viscosity to the density of the fluid.it is also called as momentum diffusivity:

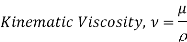
Where

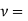Kinmeatic viscosity

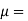Dynamic Visocosity

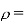Density of the fluid

1.9 Compressibility and Surface tension

Compressibility

The measure of a liquid's relative volume change when the pressure acting on it varies is called compressibility. 

B = Compressibility

V = Volume

P = Pressure

When a force acts on a fluid, it reduces its volume. The 'Bulk Modulus of Elasticity' is also used to assess this impact. The reciprocal of the Bulk Modulus of Elasticity can also be used to define the compressibility coefficient. The volume gets decreased when pressure increases so the negative sign.

Surface tension

“Surface tension is the tension of the surface film of a liquid caused by the attraction of the particles in the surface layer by the bulk of the liquid, which tends to minimise surface area”.

Surface tension is a property of liquids that arises from unbalanced molecular cohesive forces at or near a surface.

Surface tension is the tendency of liquid surfaces to shrink into the minimum surface area possible. Surface tension allows insects (e.g., water striders), to float and slide on a water surface without becoming even partly submerged.

.

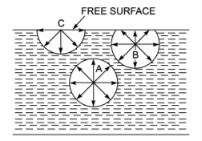
At liquid–air interfaces, surface tension results from the greater attraction of liquid molecules to each other (due to cohesion) than to the molecules in the air (due to adhesion).

There are two primary mechanisms in play. One is an inward force on the surface molecules causing the liquid to contract. Second is a tangential force parallel to the surface of the liquid. The net effect is the liquid behaves as if its surface were covered with a stretched elastic membrane.

Because of the relatively high attraction of water molecules to each other through a web of hydrogen bonds, water has a higher surface tension (72.8 milli newtons (mN) per meter at 20 °C) than most other liquids. Surface tension is an important factor in the phenomenon of capillarity.

Surface tension has the dimension of force per unit length, or of energy per unit area. The two are equivalent, but when referring to energy per unit of area, it is common to use the term surface energy, which is a more general term in the sense that it applies also to solids.

In materials science, surface tension is used for either surface stress or surface energy.

Formula for surface tension

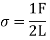
Where,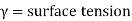

L=Length

F= force

S.I. Unit of Surface tension is N/m

The dimensional formula of surface tension is MT-2.

Examples of surface tension in action include the following: 

--formation of liquid droplets,
--the ability of a needle to float on water, 
--why bubbles are round 
--soap being used the break up water tension. 

Surface tension for various cases are

Sr	Case	Formula
1	Surface tension on liquid droplet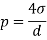
2	Surface hollow tension on bubble
3	Surface hollow tension on liquid jet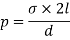
p is pressure intensity, d is diameter, is surface tension

Capillary rise

When a tiny tube is held vertically in liquid, capillarity is defined as the phenomena of a liquid surface rising or falling relative to the neighbouring general level of liquid. Capillary rise is the rise of the liquid surface, while capillary depression is the fall of the liquid surface. It is measured in cubic centimetres (cm) or millimetres (mm) of liquid. Its value is determined by the liquid's specific weight, the tube's diameter, and the liquid's surface tension.

Expression for Capillary Rise and fall. Consider a tiny diameter 'd' glass tube that is opened on both ends and immersed in a liquid, such as water. The liquid in the tube will rise above the liquid's level.

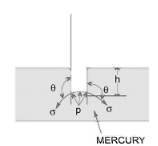
Let h= the liquid's height in the tube. The weight of a liquid of height h is balanced by the force at the liquid's surface in a state of equilibrium.  Surface tension, on the other hand, is responsible for the force at the liquid surface in the tube.               There are two force one hydrostatic force and other surface tension force which balance each other and results in capillary rise or fall

Let 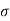= Surface tension of liquid

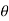= Angle of contact between liquid and glass tube.

The weight of liquid of height h in the tube = (Area of tube x h)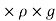

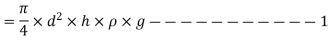
Vertical component of surface tension,

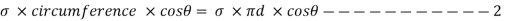
From 1 and 2

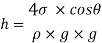
For water value of 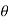is approximately equal to zero so 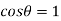and capillary rise h is

For capillary fall the force due to surface tension will be downwards, butt expression remains the same. 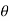 is 128 for mercury

Key Takeaway

• Surface tension is the tension of the surface film of a liquid caused by the attraction of the particles in the surface layer by the bulk of the liquid, which tends to minimise surface area

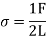
• There are two force one hydrostatic force and other surface tension force which balance each other and results in capillary rise or fall

1.10 Incompressible Flow

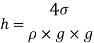
The flow is said to be incompressible if the density remains virtually constant throughout. As a result, when the flow is approximated as incompressible, the volume of each piece of the fluid remains constant during its journey. Liquid densities are essentially constant, and so liquid flow is typically incompressible. As a result, liquids are commonly known as incompressible material. To a high degree of accuracy, liquid flows are incompressible, while the degree of density fluctuation in gas flows is high. When density variations are less than 5%, which is frequently the case when Mach 0.3, gas flows can be approximated as incompressible. As a result, for speeds less than around 100 m/s, the compressibility effects of air at room temperature can be ignored. Small changes in liquid density in response to massive pressure changes can have significant repercussions. The annoying "water hammer" in a water pipe, for example, is caused by the pipe's vibrations induced by the reflection of pressure waves after the valves are suddenly closed.

Key Takeaway 

• If the density remains virtually constant, the flow is incompressible. Liquid have less variation and can be assumed incompressible, but gasses have high variation and if variation are less than 5% then only gases are assumed incompressible

1.11 Bernoulli’s Equation and Its Applications

Bernoulli’s Equation:

It states that the sum of kinetic, potential and pressure heads of a fluid particle is constant along a streamline during steady flow when compressibility and frictional effects are negligible. i.e., For an ideal fluid, total head of fluid particle remains constant during a steady-incompressible flow.

Or

Total head along a streamline is constant during steady flow when compressibility and frictional effects are negligible.

The total mechanical energy of the moving fluid comprising the gravitational potential energy of elevation, the energy associated with the fluid pressure and the kinetic energy of the fluid motion, remains constant.

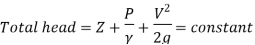
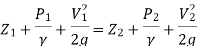
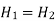
Derivation of Bernoulli’s Equation:

Fig: Bernoulli’s Theorem

Assumptions:

• The density of the incompressible fluid remains constant at both points.
• The energy of the fluid is conserved as there are no viscous forces in the fluid.

Therefore, the work done on the fluid is given as:

DW = F1dx1 – F2dx2

DW = p1A1dx1 – p2A2dx2

DW = p1dV – p2dV = (p1 – p2) dV

We know that the work done on the fluid was due to conservation of gravitational force and change in kinetic energy. The change in kinetic energy of the fluid is given as:

DK=1/2(m2v22) −1/2(m1v12) =1/2ρdV(v22−v12)

The change in potential energy is given as:

DU = mgy2 – mgy1 = ρdVg (y2 – y1)

Therefore, the energy equation is given as:

DW = dK + dU

(p1 – p2) dV = 1/2ρdV(v22−v12) + ρdVg (y2 – y1)

(p1 – p2) = 1/2 ρ(v22−v12) + ρg (y2 – y1)

Rearranging the above equation, we get

p1+1/2ρv12+ρgy1=p2+1/2ρv22+ρgy2

This is Bernoulli’s equation.

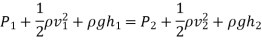
It is the important formula.

Applications of Bernoulli’s equation

Bernoulli’s equation is applied is all problems of incompressible fluid flow where energy considerations are involved, but we shall consider its applications to the following measuring devices:

1. Venturi meter
2. Pitot- tube
3. Sub-merged orifice
4. Orifice meters
5. Rotameter.

Limitation of Bernoulli’s equation

• Velocity of every liquid particle, across any section of pipe is not uniform.
• Bernoulli’s equation is not applicable for fluid with unsteady flow.
• If fluid flowing in a curved path, the energy due to centrifugal force should be taken into account.

Key Takeaway

1.12 Pitot Tube

• It is a device used for measuring the velocity of flow at any point in a pipe or a channel.
• It is based on the principle, that if the velocity of flow at a point becomes zero, the pressure there is increased due to the conservation of the kinetic energy into pressure energy.
• In its simplest form, the pitot- tube consists of a glass tube, bent at right angles as shown in fig.

Fig.: Pitot tubes

• The Lower end, which is bent though 90° is directed in the upstream direction as shown in fig.
• The liquid rises up in the tube due to the conservation of kinetic energy into pressure energy.
• The velocity is determined by measuring the rise of liquid in the tube.

P1= intensity of pressure at point (1)

V1 = velocity of flow at (1)

P2 = pressure at point (2)

V2 = velocity at point (2), which is zero

H = depth of tube in the liquid.

h = rise of liquid in the tube above the fire Surface

Applying Bernoulli’s equation at points (1) and (2)

We get

P1/ W+V1 2 / 2 g +Z1=P2/ W+V22 / 2g+Z2

But Z 1 = Z­2as points (1) and (2) are the same line and V2 =0

P1 /g= pressure Lead at (1) = H

P2 /g = pressure head at (2) = (h +H)

Substituting these values, we get

H+ V1 2 / 2 g = (h+H)

:. h= V1 2 / 2 g or v 1 = 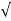(2 g h)

This is theoretical velocity.

Actual velocity is gives by (V 1) = Cv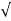 (2 g h)

Where C v= Co-efficient of pitot-tube

:. Velocity at any point V= Cv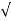 (2 g h)

1.13 Orifice Meter

• It is a device used for measuring the rate of flow of a fluid through a pipe.
• It is a cheaper device compared to venturimeter
• It also works on the same principle as that of venturimeters.
• It consists of a flat circle plate which has a circular shape edged holed called orifice, which is concentric with the pipe.
• The orifice diameter is kept generally 0.5 times the diameters of the pipe, though it may vary from 0.4 to 0.8 times the pipe diameters.
• Velocity at vena contracta  V= Cv (2 g h)

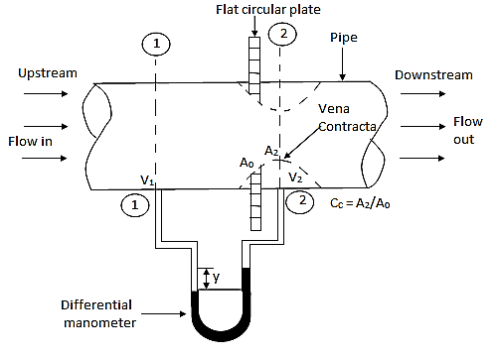
Fig.: Orifice meter

1.14 Venturi meter and Bend meter

A venturi meter is a device used for measuring the rate of a flow of a fluid flowing through a pipe it consists of three parts:

1. A short converging part,
2. Throat, and
3. Diverging Part

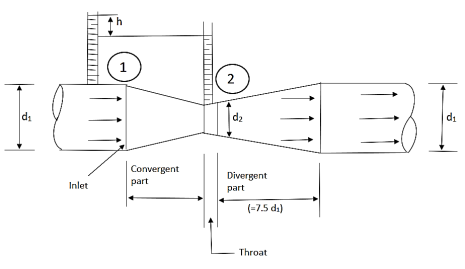
Fig.: Venturimeter

It is based on the principle of Bernoulli’s equation.

Expression for Rate of flow through venturimeter:

Consider a venturimeter fitted in a horizontal pipe through which a fluid is following as shown in fig.

Let d 1 = diameter at inlet or at section (1)

P 1= pressure at section (1)

V 1= velocity of fluid at section (1)

A 1= area of section (1) =π/4. D2

And d 2, P 2, V 2, a 2 are corresponding values at section (2)

Applying Bernoulli’s equation at section (1) and (2) we get

P1/ 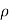g+V12 /2g+Z1=P2 / g+V22 /2g+Z2

As pipe is horizontal hence z 1 = z2

P1/ 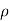g+V12 /2g =P2 / g+V22 /2g

(P1 – p 2)/ 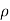g = V22 /2g - V12 /2g

But (P1 – p 2)/ g is the difference of pressure heads at section land 2 and it is equal to h 

∴ (P1 – p 2)/ 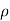g =h

Substituting this value of (P1 – p 2)/ 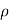g in the above eqn we get.

∴ h = V22 /2g - V12 /2g…………...  (1)

Now applying continuity equation at section 1 and

a 1 v 1 = a 2 v 2

∴ v 1 = a 2 v 2 / a 1

Substituting this value of v 1 in equation 1

h= V22 /2g – (a 2 v 2 / a 1) 2 / 2 g

h= V22 /2g [ (a 12 –a 22 )/ a 12 ]

V22 = (2 g h a 12 )/ (a 12 –a 22)

Q = a2 v 2

= [a 1 a 2 / 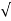( a 12 –a 22 ) ] * 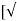( 2 g h ) ]

Above equation gives the discharge under ideal conditions and is called, Theoretical discharge Actual discharge will be less than theoretical discharge.

Q act = C d * [a 1 a 2 / 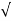( a 12 –a 22)] * 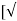(2 g h)]

Where C d = co-efficient of venturimeter and its value is less than 1.

Bend meter — This basic instrument measures the velocity of water on the inside and outside of a bend. We may deduce from the energy equation that this difference in velocity corresponds to a quantifiable pressure difference.

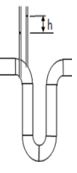
The discharge is given as

Q = Cd x a x √(2g) x h0.5

Cd ~ 0.60

1.15 Notches and Weirs

Notches:

• A notch is a sort of commencing (for the duration of the width) to the fluid go with the drift, wherein fluid flows via the lowest of notch. It is used to alter the go with the drift of fluid.
• The backside cease of the notch is commonly made sharp in order that it gives minimal resistance to the fluid go with the drift (commonly water).
• A notch is commonly made of a metallic plate and is used to alter fluid go with the drift at a small scale.

Types of Notches:

• Notches may be similarly categorized on the premise of form of commencing and on the premise of outcomes of the perimeters on Nappe (or Vein).

According to the form of commencing, notches may be categorized as-

1. Stepped notch
2. Trapezoidal notch
3. Triangular notch
4. Rectangular notch

According to the outcomes of the perimeters on Nappe (or Vein), notches may be categorized as-

1. Notch without end contraction or suppressed notch
2. Notch with end contraction

Weirs:

• A weir is a concrete or masonry shape that's positioned at the lowest side (during width) withinside the direction of fluid float. The fluid (commonly water) float above the weir.
• A weir is commonly used to modify float of water at a big scale, like in rivers or canals.
• A weir has sizable width alongside the duration of fluid float.
• Before shifting similarly in our dialogue on notches and weirs allow us to first apprehend vital phrases, with the intention to assist us in expertise varieties of both. These phrases are Nappe and Crest.

Types of Weirs:

• Weirs may be categorized on the idea of form of opening, on the idea form of Crest (or Sill) and on the idea of results of facets at the Nappe (or Vein).

On the idea of form of opening, weirs may be categorized as-

1. Trapezoidal weir (Cipolletti Weir)
2. Triangular weir
3. Rectangular weir

According to the form of the Crest, weirs may be categorized as-

1. Ogee formed weir
2. Broad crested weir
3. Narrow crested weir
4. Sharp crested weir

According the impact of facets on nappe (or vein), weirs may be categorized as-

1. Weirs without stop contraction
2. Weirs with stop contraction

1.16 Momentum Equation and Its Application to Pipe Bends

• This principle is based on the law of conservation of momentum which states, the net force acting on a fluid mass is equal to the change in momentum of flow per unit time in that direction.

By Newton's law of motion,

F = ma

But a =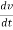

F = m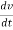

∴F =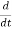(mv))

• This is known as momentum equation, Fdt=d(mv)
• This is known as impulse-momentum principle.
• It states that "The force "F" acting on a fluid of mass 'm' is a short interval of time 'dt' is equal to the change in momentum d(mv) in the direction of force".
• Application of the Momentum equation:
• The momentum equation is used to determine the resultant force exerted on the boundaries of a flow passage by a stream of flowing fluid as the flow changes its direction or the magnitude of velocity or both.

Following are the practical application of momentum equation:

1. Flow through bead pipes.
2. Jet propulsion and propellers.
3. Fluid flow through stationary and moving plates or vanes.
4. Non-uniform flow through sudden enlarged pipes.
5. Hydraulic jump in open channels,

1D momentum equation

Mass entering = Volume Density = A1(v1t)

Momentum = MassVelocity = A1(v1t)v1

Mass leaving = Volume Density = A2(v2t)

Momentum leaving the = MassVelocity = A2(v2t) v2

Resultant force on the fluid = Rate of change of momentum

F = [A2(v2t)v2 – A1(v1t)v1] / t & Q = A2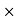v2 = A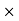1 v1

 F =  Q (v2 – v1)

2D momentum equation 

There are two component one in x and one in y direction 

In x direction

Fx =  Q (v2x – v1x)

In y direction

Fy =  Q (v2y – v1y)

The resultant force is,

F=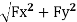

For 3 dimension

FT = FB + FW + FP =  Q (vout – vin)

FT is the total force.

FB is the force exerted on the fluid by the surrounding boundary.

FW is the force exerted on the fluid by the gravity (the weight).

FP is the force exerted on the fluid by the pressure.

-FB = Reaction force

Key Takeaway

• Momentum equation is  Fdt=d(mv)

Dimension	Momentum equation
1	F =  Q (v2 – v1)
2	Fx =  Q (v2x – v1x)    Fy =  Q (v2y – v1y)    F=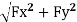

References:

1. Introduction to fluid mechanics and Fluid machines by S.K Som, Gautam Biswas, S Chakraborty.

2. Fluid mechanics and machines by R.K Bansal.

3. F. M. White, Fluid Mechanics, 6th Ed., Tata McGraw-Hill, 2008.

4. Fluid Mechanics and Its Applications by V.K. Gupta et.al.

5. Fluid Mechanics by Yunus Cengel.