Unit-1

Ordinary Differential Equation of Higher Order

1.1           Linear differential equation of nth order with constant coefficients

A homogeneous linear ordinary differential equation with constant coefficients is an ordinary differential equation in which coefficients are constants, all terms are linear, and the entire differential equation is equal to zero,

The form of second order linear differential equation with constant coefficients is,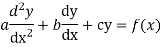
 

Where a,b,c are the constants.

 Let, aD²y+bDy+cy = f(x),    where d² = 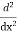,  D =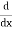

∅(D)y = f(x)   , where ∅(D)y = aD²y+bDy+cy

Here first we solve, ∅(D)y = 0, which is called complementary function (C.F)

Then we find particular integral (P.I)

P.I. = 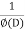f(x)

 General solution = C.F. +P.I.

Let’s do an example to understand the concept,

Example1: Solve (4D² +4D -3)y =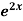 

Solution: Auxiliary equation is 4m² +4m – 3 = 0

    We get,             (2m+3)(2m – 1) = 0

     m =   ,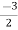

Complementary function:  CF is  A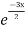+ B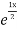

Now we will find particular integral,

P.I. = 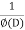f(x)

=   .

=    .

=    .

=   . =   .

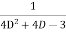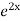
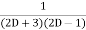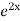
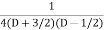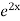
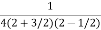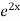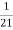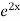
General solution is y =  CF + PI

 = A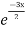+ B  .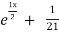

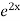
Differential operators-

D stands for operation of differential i.e.

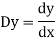
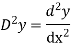
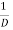stands for the operator of integration.

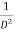stands for operation of integration twice.

Thus,

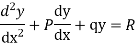
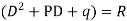
Note:-

Complete solution = complementary function + Particular integral

I.e. y=CF + PI

Method for finding the CF

Step1:- In finding the CF right hand side of the given equation is replaced by zero.

Step 2:- Let 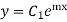be the CF of

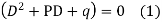
Putting the value of 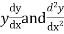in equation (1) we get

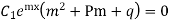
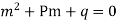
It is called auxiliary equation.

Step 3:- Roots Real and Different

If 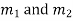are the roots the CF is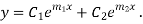

If 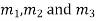are the roots then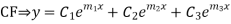

Step 4- Roots Real and Equal

If both the roots are 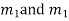then CF is

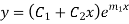
If roots are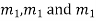

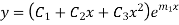
Example: Solve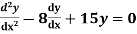

Ans. Given,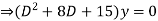

Here Auxiliary equation is

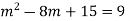
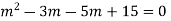
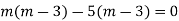
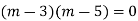
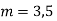
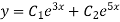
Example: Solve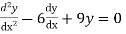

Or,

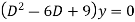
Ans. Auxiliary equation are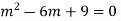

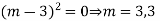
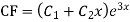
Note: If roots are in complex form i.e.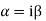

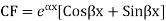
Example:  Solve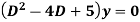

Ans. Auxiliary equation is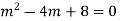

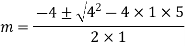
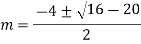
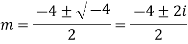
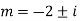
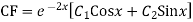
Rules to find Particular Integral

Case 1: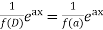

If,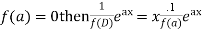

If,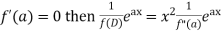

Example: Solve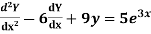

Ans. Given,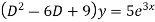

Auxiliary equation is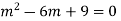

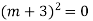
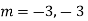
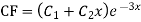
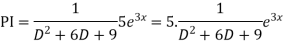
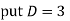
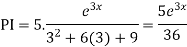
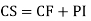
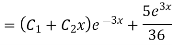
Case2: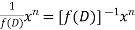

Expand 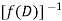by the

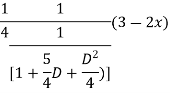
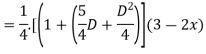
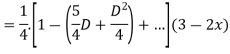
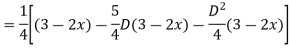
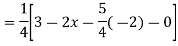
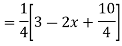
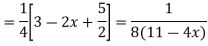
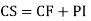
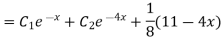
Case 3: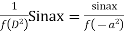

Or,

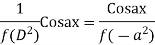
Example: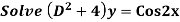

Ans. Auxiliary equation are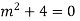

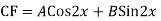
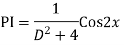
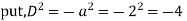
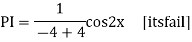
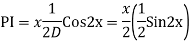
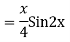
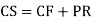
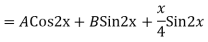
Case 4: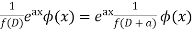

Example: Solve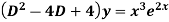

Ans. AE=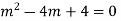

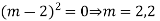
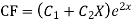
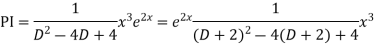
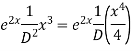
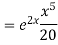
Complete solution is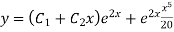

Example: Solve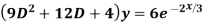

Ans. The AE is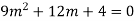

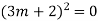
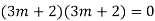
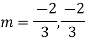
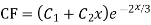
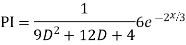
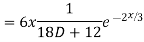
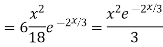
Complete solution y= CF + PI

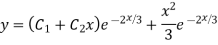
Example: Solve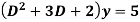

Ans. The AE is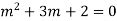

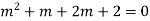
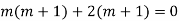
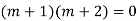
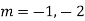
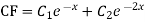
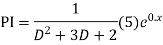
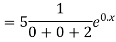
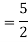
Complete solution = CF + PI

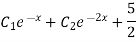
Example:  Solve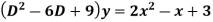

Ans. The AE is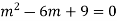

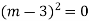
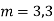
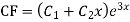
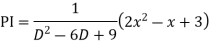
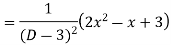
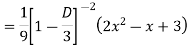
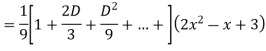
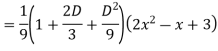
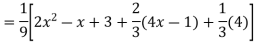
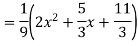
Complete solutio0n is y= CF + PI

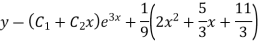
Example: Find the PI of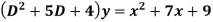

Ans.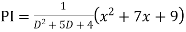

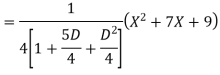
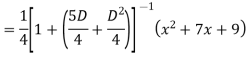
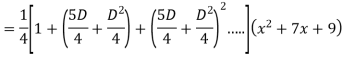
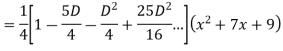
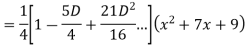
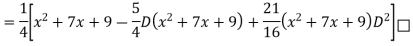
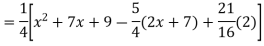
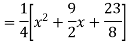
Example: solve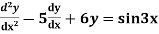

Ans. Given equation in symbolic form is

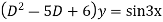
Its Auxiliary equation is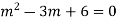

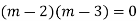
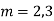
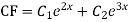
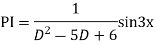
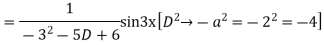
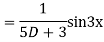
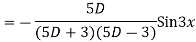
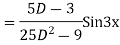
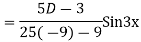
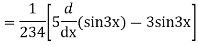
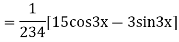
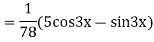
Complete solution is y= CF + PI

Example:  Solve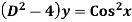

Ans. The AE is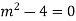

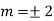
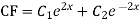
We know,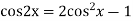

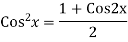
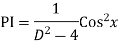
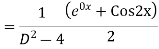
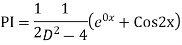
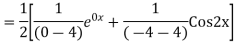
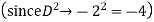
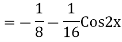
Complete solution is y= CF + PI

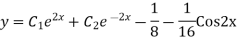
Example: Find the PI  of(D2-4D+3)y=ex cos2x

Ans.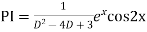

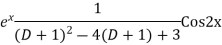
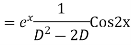
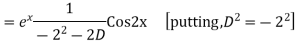
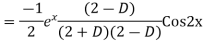
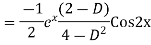
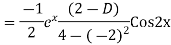
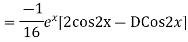
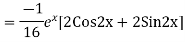
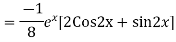
Example.  Solve(D3-7D-6) y=e2x (1+x)

 Ans. The auxiliary equation i9s

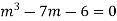
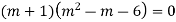
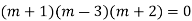
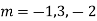
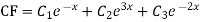
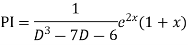
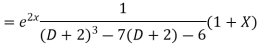
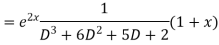
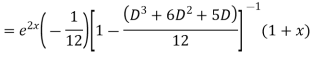
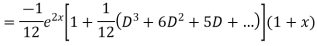
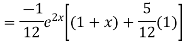
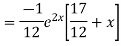
Hence complete solution is y= CF + PI

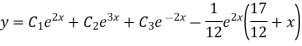
Key takeaways-

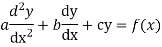
Where a,b,c are the constants.

2.     General solution = C.F. +P.I.

3.    

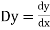
4.     

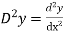
5.     Roots Real and Equal-

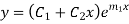
6.     Roots Real and Different-

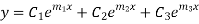
7.     If roots are in complex form i.e.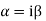

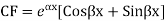
1.2 Simultaneous linear differential equations

The equation involving the derivatives of two or more dependent variables, which are the functions of a single independent variable, the equations involving their derivative is called simultaneous equation.

Such as-

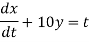
We use method of elimination to solve these types of equations.

Example 1: Solve the following simultaneous differential equations-

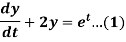
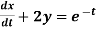....(2)

Solution:

Consider the given equations

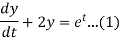
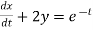....(2)

Consider eq(1),(2)

 Dx+2y = et....(1)

Dx +2x =e-t....(2)

Eliminating ‘x’ from both the equations we get,

12 2Dx + 2y = 2et

D 2Dx +D2y = e-t

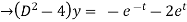
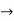y = Ae2t + Be-2t +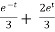

Example 2: Solve the following simultaneous differential equations-

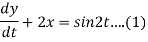
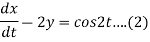
Given that x(0)=1  and y(0)= 0

Solution:

Consider the given equations,

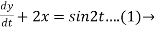Dy +2x = sin2t

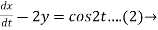Dx -2y = cos2t

By solving the above equations, we get,

(D2 +4)Y =0

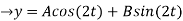
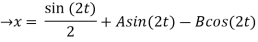
X(0) = 1, y(0) = 0

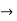A =0, B=-1

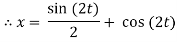
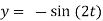
Example-3: Solve the following simultaneous differential equations-

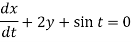
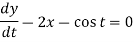
It is given that x = 0 and y = 1 when t = 0.

Sol. Given equations can be written as-

Dx + 2y = - sin t ………. (1)    and     -2x + Dy = cos t  ……… (2)

Eliminate x by multiplying (1) by 2 and (2) by D then add-

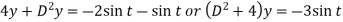
Here A.E =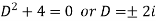

So that C.F. =

And P.I. =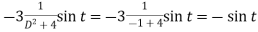

So that- 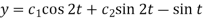   …………. (3)

And 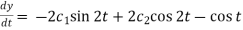  ………….. (4)

Substitute (3) in (2), we get-

 2x = Dy – cos t =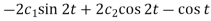

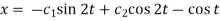  ………… (5)

When t = 0, x = 0, y = 1. (3) and (5) gives-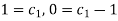 

Hence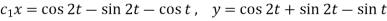

1.3 Second order linear differential equations with variable coefficients

Linear differential equation are those in which the independent variable and its derivative occur only in the first degree and are not multiplied together.

Thus the general linear differential equation of the n’th order is of the form

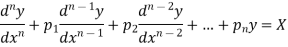
Where 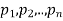and X are function of x.

Linear differential equation with constant co-efficient are of the form-

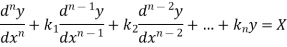
Where 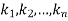are constants.

Rules to find the complementary function-

To solve the equation-

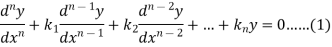
This can be written as in symbolic form-

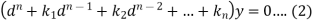
Or-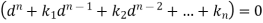
 

It is called the auxiliary equation.

Let 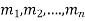be the roots-

Case-1: If all the roots are real and distinct, then equation (2) becomes,

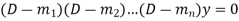
Now this equation will be satisfied by the solution of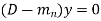

This is a Leibnitz’s linear and I.F. =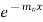

Its solution is-

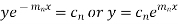
The complete solution will be-

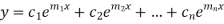
Case-2: If two roots are equal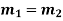

Then complete solution is given by-

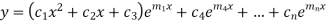
Case-3: If one pair of roots be imaginary, i.e. 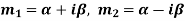then the complete solution is-

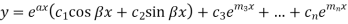
Where 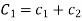and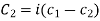

Case-4: If two points of imaginary roots be equal-

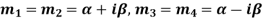
Then the complete solution is-

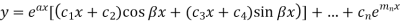
Example-Solve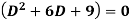

Sol.

Its auxiliary equation is-

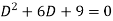
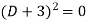
Where-

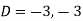
Therefore, the complete solution is-

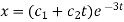
Inverse operator-

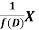is that function of x, not containing arbitrary constants which when operated upon gives X.

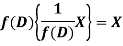
So that 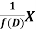satisfies the equation f(D)y = X and is, therefore, its P.I.

f(D) and 1/f(D) are inverse operator.

Note-

1.

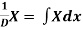
2.

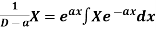
Rules for finding the particular integral-

Let us consider the equation-

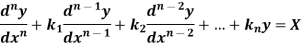
Or in symbolic form-

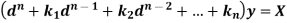
So that-

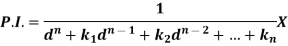
Now-

Case-1: When X =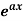

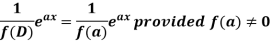
In case f(a) = 0, then we see that the above rule will not work,

So that-

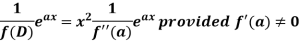
Example: Find the P.I. of (D + 2)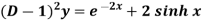

Sol.

P.I. =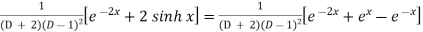

Now we will evaluate each term separately-

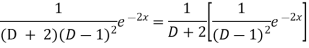
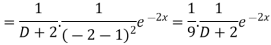
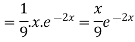
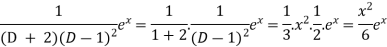
And

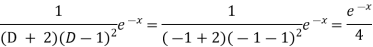
Therefore-

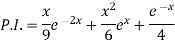
Example: Solve (D – D’ – 2 ) (D – D’ – 3) z =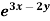

Sol.

The C.F. will be given by-

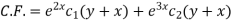
Particular integral-

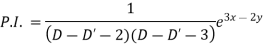
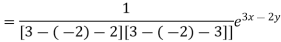
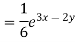
Therefore the complete solution is-

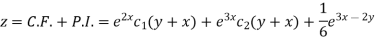
Case-2: when X = sin(ax + b) or cos (ax + b)

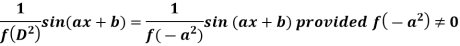
In case 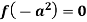then the above rule fails.

Now-

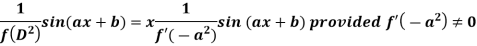
And if

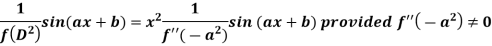
Similarly-

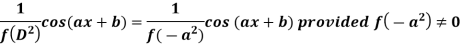
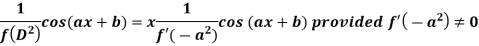
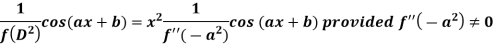
Example: Find the P.I. of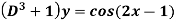

Sol.

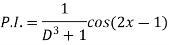
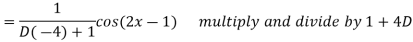
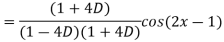
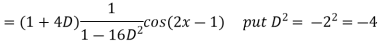
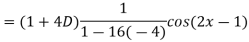
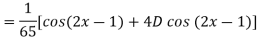
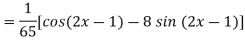
Example: Find the P.I. of (D + 1) (D + D’ – 1)z = sin (x + 2y)

Sol.

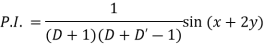
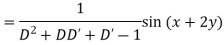
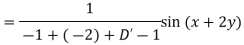
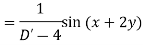
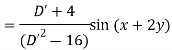
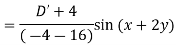
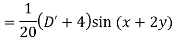
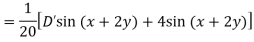
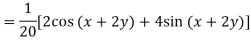
Example: Find P.I. of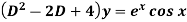

Sol. P.I =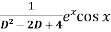

Replace D by D+1

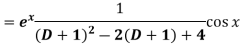
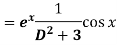
Put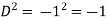

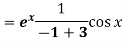
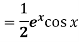
Key takeaways-

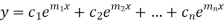
2.     If two roots are equal 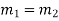Then complete solution is given by-

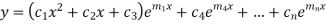
3.     If one pair of roots be imaginary, i.e. 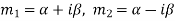then the complete solution is-

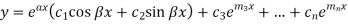
 Where 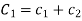and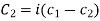

4.     If two points of imaginary roots be equal-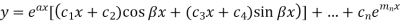
 

1.4 Solution by changing independent variable

Let

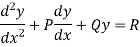
Be the differential equation where P, Q, R are the functions of x.

If y = u(x) is the solution we know, then put y = uv in it.

It reduces the diff. Equation to one of first order in dv/dx which can be solved completely.

Note-

1 if 1+P+Q = 0, Then 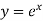is a solution.

2. if 1-P+Q = 0, Then 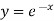is a solution.

3. if P+Qx = 0, Then 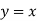is a solution.

Example: Solve

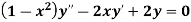
It is given that y = x is a solution.

Sol.

Suppose y = xv so that-

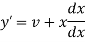
And

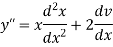
Now put these values in the given equation, we get-

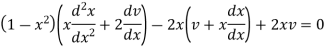
Or

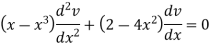
Or

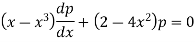
Where p = dv/dx

On integrating, we get-

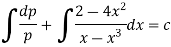
Or

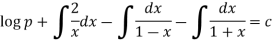
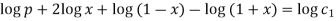
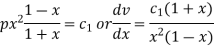
Again integrating,

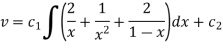
Or

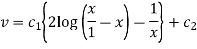
Hence the required solution-

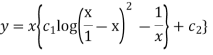
Equation which can be solved by changing the independent variable-

Consider the equation-

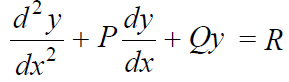
Lets change the independent variable x to z and z = f(x)

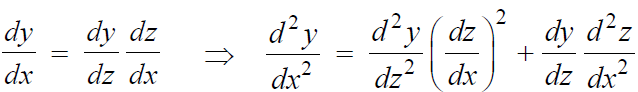
Now put these values in the equation, we get-

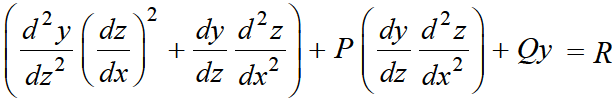
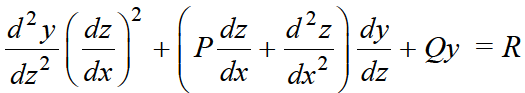
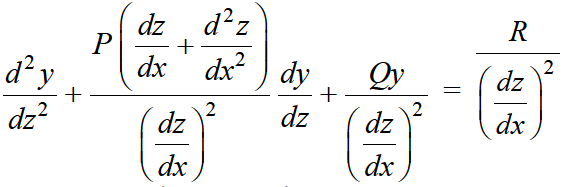
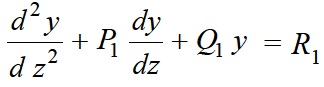........ (1)

here

,

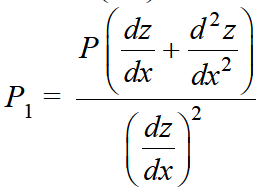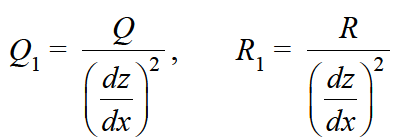
Equation-1 can be solved by taking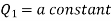

Example: Solve-

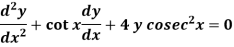
Sol.

Here P = cot x and Q =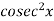

Choosing z so that

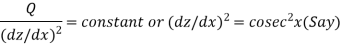
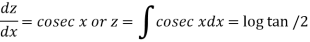
Changing the independent variable x to z, we get-

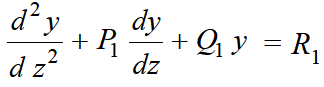......(1)

Where-

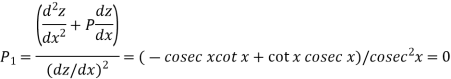
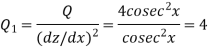
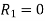
Equation(1) becomes-

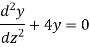
Its sol. Is-

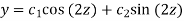
i.e.

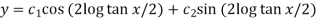
Which is the required solution

Key takeaways-

1 if 1+P+Q = 0, Then 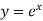is a solution.

2. if 1-P+Q = 0, Then 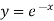is a solution.

3. if P+Qx = 0, Then 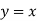is a solution

1.5 Reduction of order, Normal form

Let 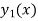is known non-trivial solution of the second order homogeneous linear equation-

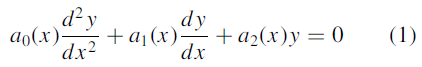
Then the second linearly independent non-trivial solution

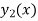 of (1) can be obtained by the method

Of reduction of order. This method makes use of a

Transformation of the form

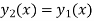
which reduces the second order equation (1) to a first

order differential equation which is then integrate for

the unknown function v(x).

write again (1) in the standard form

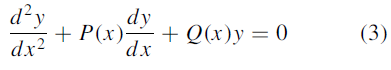
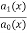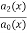Where P(x) = , Q = with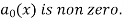

Differentiating (2) w.r.t. x, we get-

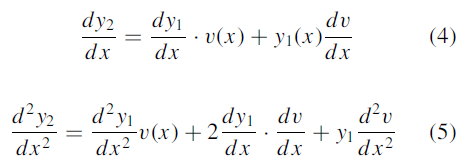
Put (2), (4), (5) in (3), we get-

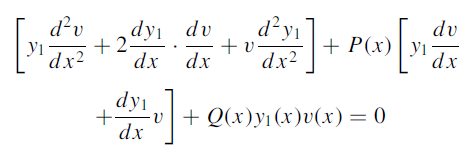
Rewriting-

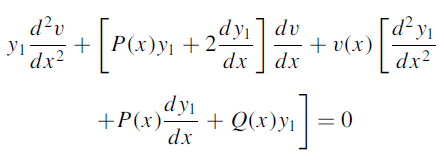
Here 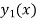is a known solution of (1), then the last term in above equation becomes zero.

Let introduce-

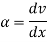
the above equation reduces to a first order

linear differential equation in the new dependent

variable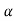 , given by

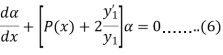
Separating the variables and integrating, we get

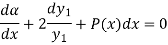
Or

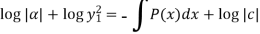
Then-

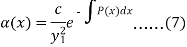
Choosing, c = 1

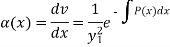
Now on integrating-

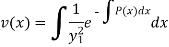
So that we get the required second solution -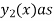

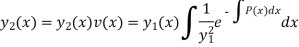
Hence 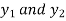from the basis of diff equation (1) and general solution of (1) is-

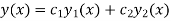
Example: Obtain the basis for the equation 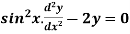if 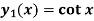is a solution.

Sol.

The standard form of the equation will be-

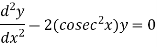
So that-

P(x) = 0. The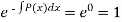

Now-

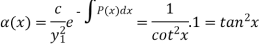
So-

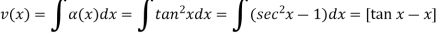
Then

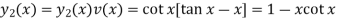
The basis consisting of the two linearly independent solutions is-

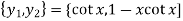
Example on normal norm-

Example: Solve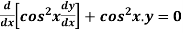

Sol.

Here we have-

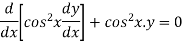
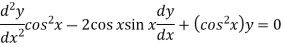
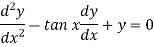
Here,

P = -2 tan x, Q = 1, R = 0

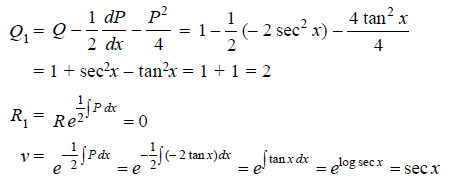
Normal equation is-

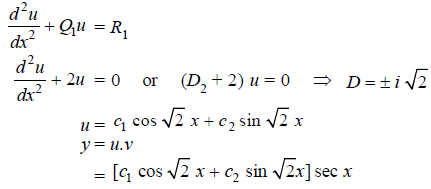
Example: Solve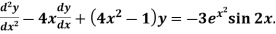

Sol.

Here we have-

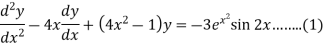
Here p = -4x, Q = 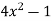, R =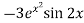

Now in order to remove the first derivative x,

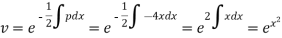
Now on putting y = uv, then normal equation is-

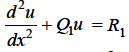.............(2)

Where

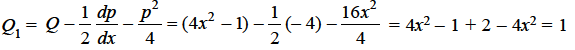
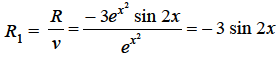
Equation (2) becomes-

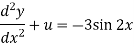
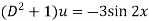
Auxiliary equation-

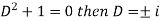
C.F.-

1.6 Method of variation of parameters

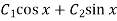
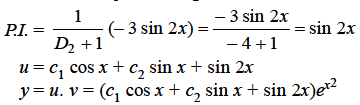
Method of variation of parameters-

Consider a second order LDE with constant co-efficients given by

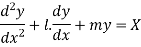
Then let the complimentary function 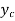is given by

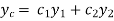
Then the particular integral is

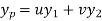
Where u and v are unknown and to be calculated using the formula

u=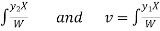

Example-1: Solve the following DE by using variation of parameters-

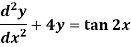
Sol. We can write the given equation in symbolic form as-

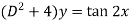
To find CF-

It’s A.E. is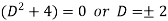

So that CF is-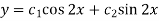     

To find PI-

Here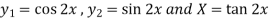

Now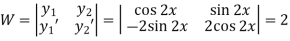

Thus PI =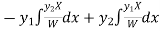 

            = 

            = 

             = 

             = 

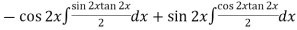
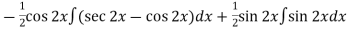
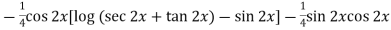
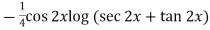
So that the complete solution is-

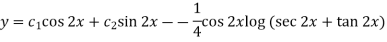
Example-2: Solve the following by using the method of variation of parameters.

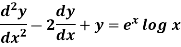
Sol. This can be written as-

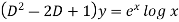
C.F.-

Auxiliary equation is-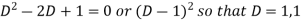

So that the C.F. will be-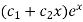

P.I.-

Here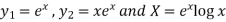

Now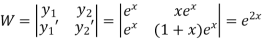

Thus PI =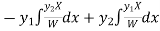 

            = 

            = 

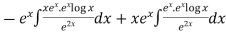
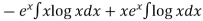
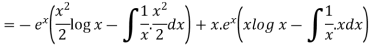
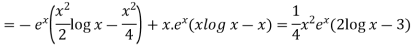
So that the complete solution is-

1.7 Cauchy-Euler equation

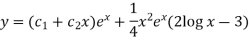
An equation of the form

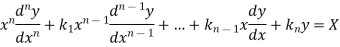
Here X is the function of x, is called Cauchy’s homogeneous linear equation.

Example-1: Solve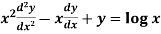

Sol. As it is a Cauchy’s homogeneous linear equation.

Put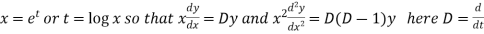

Then the equation becomes [D(D-1)-D+1]y = t   or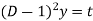

Auxiliary equation-

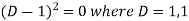
So that-

   C.F.=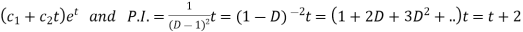

Hence the solution is- 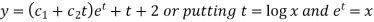, we get-

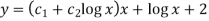
Example-2: Solve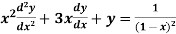

Sol. On putting 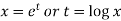so that,

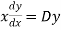and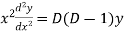

The given equation becomes-

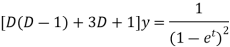
Or it can be written as-

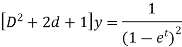
So that the auxiliary equation is-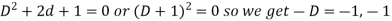

C.F. =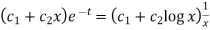

Particular integral-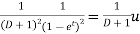

Where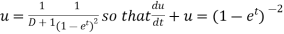

It’s a Leibnitz’s linear equation having I.F.=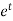

Its solution will be-

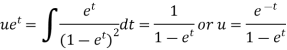
P.I. =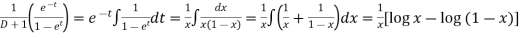

       =

So that the complete solution is-

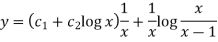
An equation of the form-

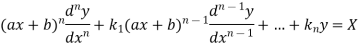
Is called Legendre’s linear equation.

Example-3: Solve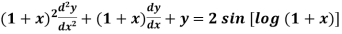

Sol. As we see that this is a Legendre’s linear equation.

Now put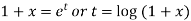

So that-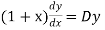

And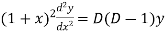

Then the equation becomes- D (D – 1)y+ Dy + y = 2 sin t

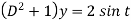
Its auxiliary equation is-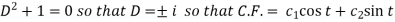

And particular integral-

               P.I. =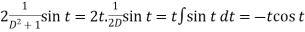

Note -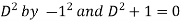

Hence the solution is -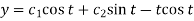

Key takeaways-

Cauchy’s homogeneous linear equation-

1.8 Series solutions (Frobenius Method)

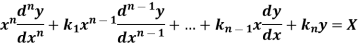
We know that the solution of the differential equation-

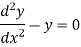
Are

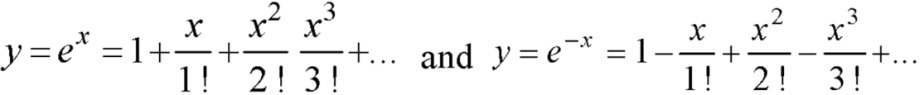
These are the power series solutions of the given differential equations.

Ordinary Point-

Let us consider the equation-

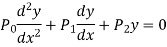
Here 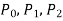are polynomial in x.

X = a is an ordinary point of the above equation if 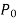does not vanish for x = a.

Note- If 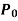vanishes for x = a, then  x =  a is a singular point.

Solution of the differential equation when x = 0 is an ordinary point, which means 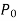does not vanish for x = 0.

1. Let 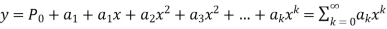be the solution of the given differential equation.

2. Find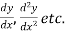

3.

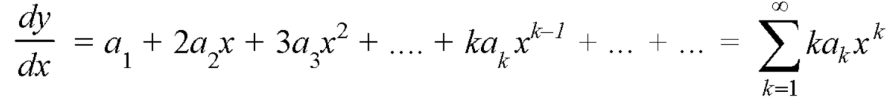
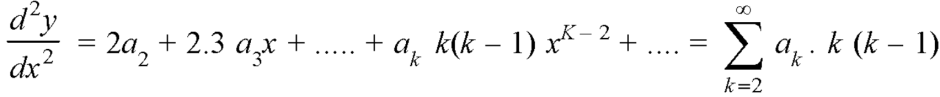
4. Substitute the expressions of y, 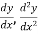etc. in the given differential equations.

5. Calculate 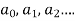Coefficients of various powers of x by equating the coefficient to zero.

6. Put the values of 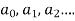In the differential equation to get the required series solution.

Example- Solve

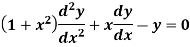
Sol.

Here we have-

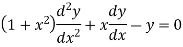
Let the solution of the given differential equation be-

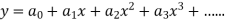
Since x = 0 is the ordinary point of the given equation-

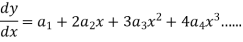
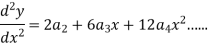
Put these values in the given differential equation-

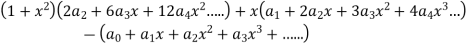
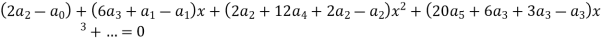
Equating the coefficients of various powers of x to zero, we get-

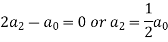
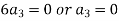
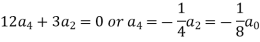
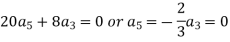
Therefore the solution is-

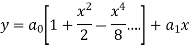
Example: Solve in series the equation-

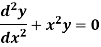
Sol.

Here we have-

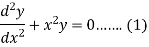
Let us suppose-

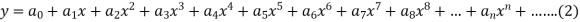
Since x = 0 is the ordinary point of (1)-

Then-

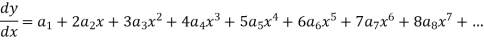
And

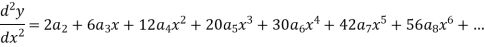
Put these values in equation (1)-

We get-

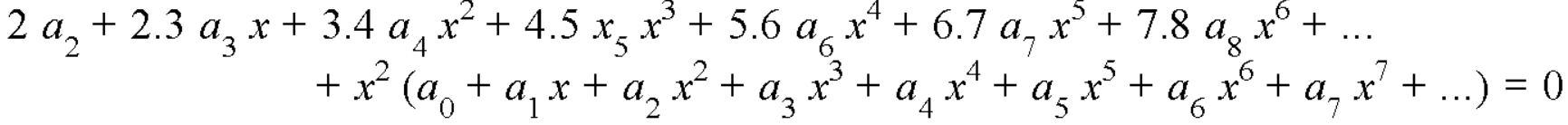
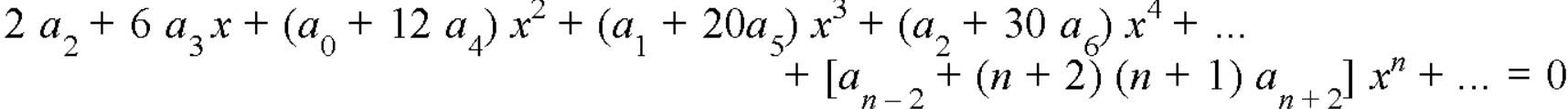
Equating to zero the coefficients of the various powers of x, we get-

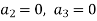
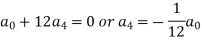
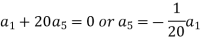
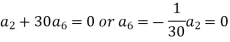
And so on….

In general we can write-

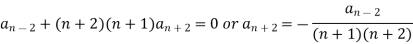
Now putting n = 5,

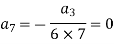
Put n = 6-

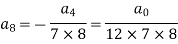
Put n = 7,

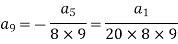
Put n = 8,

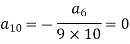
Put n = 9,

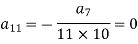
Put n = 10,

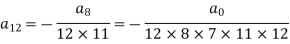
Put the above values in equation (1), we get-

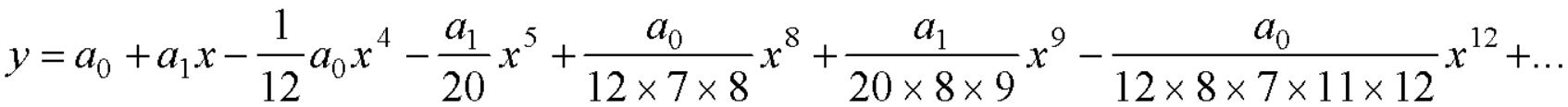
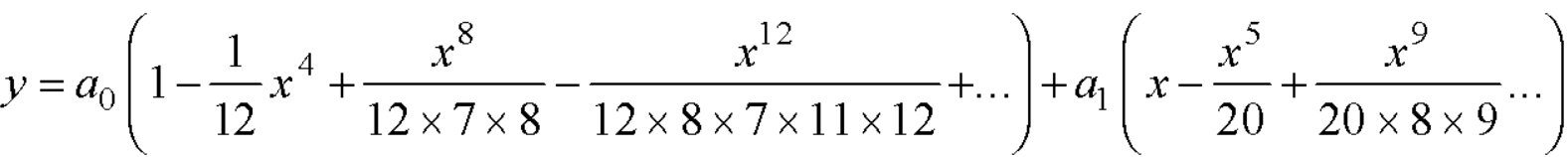
Frobenius method-

This method is also called generalized power series method.

If x = 0 is a regular singularity of the equation.

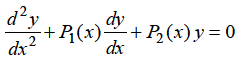……..(1)

Then the series solution is-

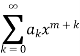
Which is called Frobenius series.

On equating the coefficient of lowest power of x in the identity to zero, we get a quadratic equation in ‘m’.

We will get two values of m. The series solution of (1) will depend on the nature of the roots of the indicial equation-

Case-1: when roots m1 and m2 are distinct and these are not differing by an integer-

The complete solution in this case will be-

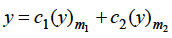
Case-2: when roots m1 and m2 are equal-

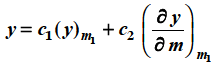
Case-3: when roots are distinct but differ by an integer-

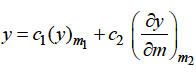
Case-4: Roots are distinct and differing by an integer, making some coefficient indeterminate-

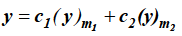
Example: Find solution in generalized series form about x = 0 of the differential equation

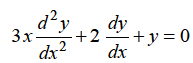
Sol.

Here we have

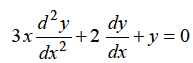………… (1)

Since x = 0 is a regular singular point, we assume the solution in the form

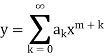
So that

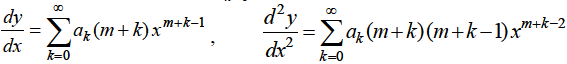
Substituting for y, 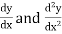in equation (1), we get-

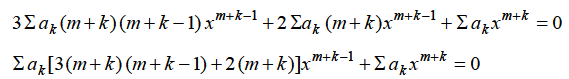…..(2)

The coefficient of the lowest degree term 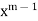in (2) is obtained by putting k

= 0 in first summation only and equating it to zero. Then the indicial equation is

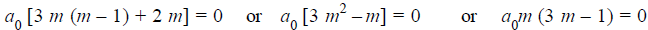
Since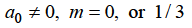

The coefficient of next lowest degree term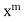in (2) is obtained by putting

k = 1 in first summation and k = 0 in the second summation and equating it to zero.

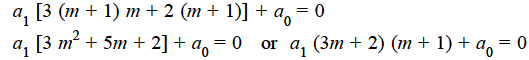
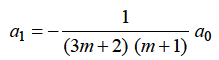
Equating to zero the coefficient of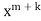 the recurrence relation is given by

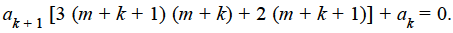
Or

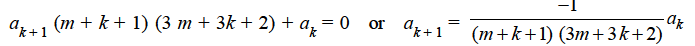
Which gives-

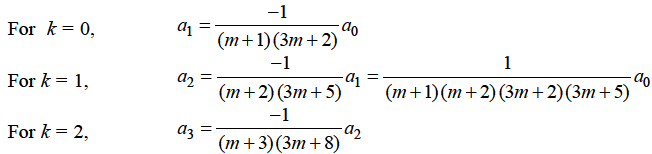
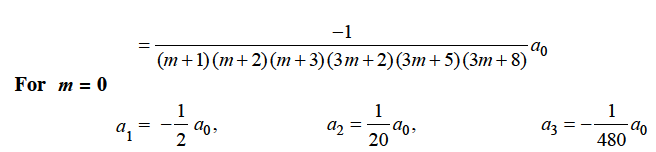
Hence for-

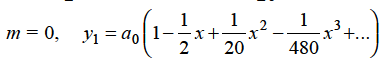
Form m = 1/3-

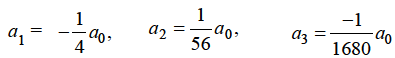
Hence for m = 1/3, the second solution will be-

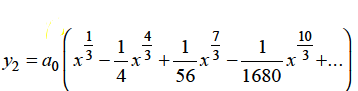
The complete solution will be-

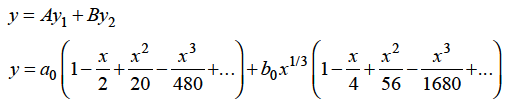
Key takeaways-

If

vanishes for x = a, then  x =  a is a singular point.

If x = 0 is a regular singularity of the equation.

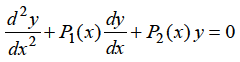……..(1)

Then the series solution is-

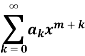
Which is called Frobenius series.

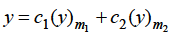
2.     When roots m1 and m2 are equal-

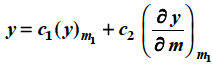
3.     When roots are distinct but differ by an integer-

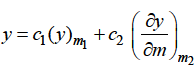
4.     Roots are distinct and differing by an integer, making some coefficient indeterminate-

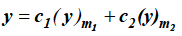
References