Unit - 4
Introduction to Compression Members
Compression contributors are structural factors which can be driven collectively or bring a load, extra technically they're subjected best to axial compressive forces. That is, the masses are implemented at the longitudinal axis via the centroid of the member pass segment, and the load over the pass sectional place offers the pressure at the compressed member.
In homes, posts and columns are nearly continually compression contributors as are the top chord of trusses.
A structural member loaded axially in compression is normally referred to as a compression member.
Vertical compression contributors in homes are referred to as columns, posts or stanchions.
A compression member in roof trusses is referred to as struts and in a crane is referred to as a boom.
Columns which are short are subjected to crushing and behave like members under pure compression. Columns which are long tend to buckle out of the plane of the load axis.
The most important styles of column bases are the following:
(i) Slab base
(ii) Gusseted base
(i) Slab Base:
In this association the column stands at once over a metal base plate which rests over a concrete basis.
The base plate is attached to the column flanges with connecting angles with the aid of using welding or bolting.
The column-base plate unit is geared up within side the concrete basis with basis bolts.
(ii) Gusseted Base:
Gusseted base plates are used for columns sporting heavy loads. In this example fastenings are used to connect the bottom plate and the column within side the shape of gusset plates, angles etc.
Compression contributors of roof trusses are composed of unmarried angles or double angles. These contributors can be non-stop contributors (just like the fundamental rafter of the roof truss) or discontinuous contributors (just like the vertical and diagonal contributors of the truss).
The powerful duration KL of the compression contributors can be taken as zero.7 to 1. Zero instances the space among centers of connections relying at the diploma of cease restraint provided.
In the case of contributors of trusses for buckling within side the aircraft perpendicular to the aircraft of the truss, the powerful duration, KL will be taken as the space among the centers of intersection.
Buckling of columns are largely depends upon support conditions. In each case there is a portion of the length of the compression member bends from the points of contra flexure.
The effective length KL of a compression member is the distance between these points. Therefore, it should be derived from the actual length and end / support conditions. Tables 1 and 2 the effective length (kl) of columns and struts respectively for various end conditions.
Boundary condition | Schematic representation | Effective length | |||
At one end | At the other end | ||||
Translation | Rotation | Translation | Rotation | ||
Restrained | Restrained | Free | Free |  | 2.0 L |
Free | Restrained | Restrained | Free | 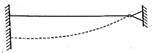 | 2.0 L |
Restrained | Free | Restrained | Free |  | 1.0L |
Restrained | Restrained | Free | Restrained | 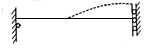 | 1.2 L |
Restrained | Restrained | Restrained | Free |  | 0.8L |
Restrained | Restrained | Restrained | Restrained | 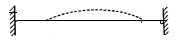 | 0.65L |
Key takeaways:
- Buckling of columns are largely depends upon support conditions.
- In each case there is a portion of the length of the compression member bends from the points of contra flexure.
- The effective length KL of a compression member is the distance between these points.
The tendency of a compression member to buckle is usually measured by its slenderness ratio. It is given by
Formula,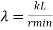 
Where,
KL= Effective length of a member
Rmin =Radius of gyration about minor axis = NA
I= Moment of inertia of a member.
The maximum slenderness ratio should be under a limit of permissible slenderness ratio of compressive member given in Table 3 of IS 800-2007.
Key takeaways:
- The tendency of a compression member to buckle is usually measured by its slenderness ratio.
- It is given by Formula,
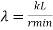
- The maximum slenderness ratio should be under a limit of permissible slenderness ratio of compressive member given in Table 3 of IS 800-2007.
As the compressive strength (P) decreases with increase in the slenderness-ratio, a section for the compression member should be such that it has the maximum moment of inertia for the same sectional area. So, it is preferable to choose the section having same moment of inertia about both the principle axes. Some of the sections used for compression members are shown in Fig.
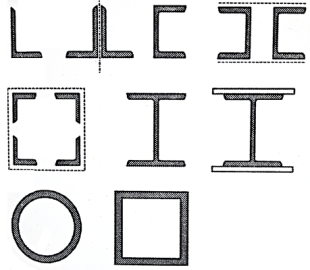
Key takeaways:
- As the compressive strength (P) decreases with increase in the slenderness-ratio, a section for the compression member should be such that it has the maximum moment of inertia for the same sectional area.
- So, it is preferable to choose the section having same moment of inertia about both the principle axes
1. Flexural buckling
2. Local buckling
3. Torsional buckling
1. Flexural buckling:
Flexural Buckling (additionally known as Euler Buckling) is the number one kind of buckling members are subjected to bending or flexure when they grow to be unstable
2. Local Buckling
This takes place while some component or elements of x-phase of a column are so skinny that they buckle domestically in compression earlier than different modes of buckling can occur
3. Torsional Buckling
These columns fail by twisting (torsion) or blended impact of tensional and flexural buckling
Key takeaways:
1. Flexural buckling
2. Local buckling
3. Torsional buckling
Classification of cross section
Cross section | Limit | Buckling about axis | Buckling class |
Rolled I section | h/bf>1.2:tf<40mm 40<mm<tf<100mm | z-z y-y z-z y-y | A B B C |
Welded I section | Tf<40mm Tf>40mm | z-z y-y z-z y-y | b c c d |
Hollow section | Hot rolled | Any | a |
| Cold rolled | Any | B |
Welded box section | Generally (expected as below) | Any | B |
| Thick welds and b/tf<30 h/tf<30 |
z-z y-y |
c c |
Channel, angle, T and Solid sections |
| Any | C |
Built up member |
| Any | c |
Compression Members: Structural factors which are subjected to axial compressive forces most effective are known as columns. Columns are subjected to axial masses through the centroid.
• Stress: The pressure within side the column cross-segment may be calculated as
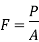
This perfect country is in no way reached. The stress-country could be non-uniform because of: Accidental eccentricity of loading with appreciate to the centroid - Member out-of–straightness (crookedness), or - Residual stresses within side the member cross-segment because of fabrication processes. Accidental eccentricity and member out-of-straightness can purpose bending moments within side the member. However, those are secondary and are generally ignored. Bending moments can't be omitted if they're performing at the member. Members with axial compression and bending second are referred to as beam-columns
Examples:
1) Check the adequacy of an ISA 70 x 70 x 6 @ 6.3 kg/m to factored axial compressive load opf 160kn. Two angles are connected on either side of 8 mm thick gusset plate by 4 numbers of M20 black bolts of 4.6 grades. The effective length of strut is 2.3 m
Solution:
1) properties of 2 ISA 70 x70x6 @ 6.3 kg/m
A= 1260 mm^2, rzz= 21.4 mm, ryy= 31.7 mm
2) slenderness ratio
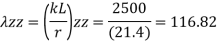
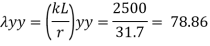
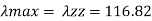
3) Buckling class
Using table 10, IS 800-2007
Buckling class of an angle= C
4) Design compressive stress (Fcd)
Kl/r | Fy=250 |
110 | 94.6 |
116.82 | Fcd |
120 | 83.7 |
By interpolation
Fcd = 87.16 MPa
5) Design compressive strength
Pd= Ae x Fcd = 1260 X 87.16 = 109.82 kN
Hence section is adequate.
2) Determine the design strength of a column section ISLB 500 @ 75 kg/m with the effective length of the column as 5m. Assume buckling axis as z-z axis and yield stress of steel fy = 250 Mpa
Solution:
Properties of section – ISLB 500 @ 75 kg/m
Area= 9559 mm^2, rzz= 201 mm
Effective length KL= 5000 mm
3) Slenderness ratio
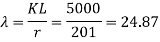
4) Buckling compressive stress (fcd)
From table 9(a) IS 800-2007
KL/r | Fcd |
20 | 226 |
24.87 | ? |
30 | 220 |
By interpolation
Fcd = 223.07 MPa
5) Design compressive strength (Pd)
Pd= Ae.fcd= 9550 x 223.07 = 2130.3 kN
Pd= 2130.3 kN
To design a compression member, length, end conditions and load it has to support are required.
The designer is supposed to select a section which provides a large radius of gyration without providing more area and in which the design compressive strength (P) just exceeds the factored compressive load.
To find compressive strength, the area of cross section and radius of gyration must be known. So cut of these two unknowns, one unknown should be assumed and compute other. Then section is checked
Step (1): The design compressive stress (F) is to be assumed.
There is no proper estimation of slenderness ratio for any length and support condition, therefore for a trial, range of F for slenderness ratio given below.
(a) For Angle strut: The slenderness ratio varies from 110 to 130. Hence assume F in between 80 to 110
(b) For rolled beam sections: The slenderness ratio varies from 70 to 100. Hence assume F in between 110 to 180 MPa.
Notes: For a column with heavy factored load and large lengthy height, required large radius of gyration. Therefore, built up sections are required to the selected for design
Step (2): Selection of section:
A required= P/fcd
Step (3): Classification of section
Step (4): Knowing and conditions and determine effective length (kl). Also find out slenderness ratio.
Step (5): Determine buckling class using table 10 of IS 800-2007
Step (6): Determine design compressive stress (f)
Step (7): Determine design compressive strength P
Using Pd= Ae.fcd>P Safe
Step (8): Revise the section if P, <P (factored load) till it will safe.
Key takeaways:
Step (1): The design compressive stress (F) is to be assumed.
Step (2): Selection of section:
A required= P/fcd
Step (3): Classification of section
Step (4): Knowing and conditions and determine effective length (kl). Also find out slenderness ratio.
Step (5): Determine buckling class using table 10 of IS 800-2007
Step (6): Determine design compressive stress (f)
Step (7): Determine design compressive strength P
Using Pd= Ae.fcd>P Safe
Step (8): Revise the section if P, <P (factored load) till it will safe.
Built-up sections are preferred instead of rolled steel sections for a column in industrial buildings because.
(1) Span and height of industrial buildings are large, so the load on the columns are enough large such that available rolled steel sections are unable to sustain loads.
(2) Also, built up sections are designed such that the radius of gyration about two principal axes is same.
(3) Lacing and battening in built up column restrain lateral buckling of column.
(4) Finally, design strength of built-up sections more than available rolled steel sections.
Lacing and battening are used in built up section of column is large for toll purpose. (1) To restrain lateral buckling of column section as the height of built-up column is large.
(2) The sections of built-up column to act a single section.
Design of Laced Column
Procedure
(A) Design of Column
1) The design compressive stress is assumed. It is difficult for an excellent assumption of slenderness ratio or design compressive stress. Is in the range of 125 to 185 MPa assumed for f, = 250 MPa of steel.
2) Selection of cross section:
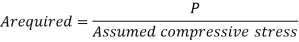
Where,
A = Cross-sectional area in mm²
P= Factored axial compressive force.
A suitable section comprising of two channels of four channels or four angles or two I section with or without extra plates as required is selected from steel table.
(3) Effective length (kL) depends upon end /support conditions is determined and the slenderness ratio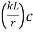
is determined.
The effective slenderness of laced column should be taken as in order to account for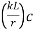 
ratio 1.05 times 
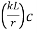deformation effect.
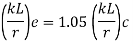
(4) For the estimated value of the slenderness ratio the design compressive stress (f) is computed from Table 9(a), (b), (c) and (d).
5) The design compressive strength is computed. It should be more than the factored load over the section.
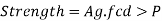
(6) The sections are so placed that the radius of gyration of section about the axis perpendicular to the plane of lacing is not less than the radius of gyration about the axis in the plane of lacing. This is achieved by making ryy>rzz
(B) Design of Lacing Bar
(1) Angle of inclination of lacing bar with the longitudinal axis of the component member should be kept between 40"-70". As an initial trial value 0 may be assumed to be 45° and the spacing of lacing bars a, r, is calculated.
(2) The maximum spacing of lacing bars a, should be such that minimum slenderness ratio of the component member a/r, is not greater than 50 or 0.7 times the slenderness ratio of the member as a whole,
Where, a, = is the length of component member.
Ryy=radius of gyration @ y-y axis.
(3) The lacing for compression members should be proportioned to resist a total transverse shear v₁= 2.5% of axial load. This shear v, is divided equally in all parallel planes N in which there is shear resisting elements, such as lacing or continuous plates. Hence v/N is the transverse force to which the lacing is subjected N=2 for two channels laced on both faces.
The compressive force in the lacing bar
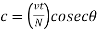For single lacing system
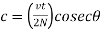For double lacing system
The section of the lacing flat initially assumed and then check for safety.
(1) Diameter of bolt or rivet assumed (d)
(ii) Width = b > 3d
(iii) Thickness = t
For single lacing
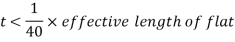
For double lacing
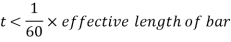
(6) rmin of lacing flat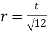 
(7) 
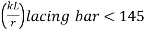
Where, KL = Distance between inner end bolts (for single lacing)
= 0.7 x L for double lacing
= 0.7 x inner length of plate weld.
(8) Design compressive stress (f) is determined and also design compressive strength of lacing plate is calculated which should be more than 'c'.
(9) Determine tensile strength of lacing plate using yielding of gross cross-section and rupture at net cross section.
(10) Design the connection (bolted or welded)
(11) Detailing.
Key takeaways:
1) Span and height of industrial buildings are large, so the load on the columns are enough large such that available rolled steel sections are unable to sustain loads.
2) Also, built up sections are designed such that the radius of gyration about two principal axes is same.
3) Lacing and battening in built up column restrain lateral buckling of column.
In this case the components of the composite section are connected by lacing. Lacing consists of connecting the components of the column by a system of generally flat plates. (In some cases, angles and channels are also used as lacings). Lacing plates may be 50 mm to 75 mm wide and 8 mm to 10 mm thick.
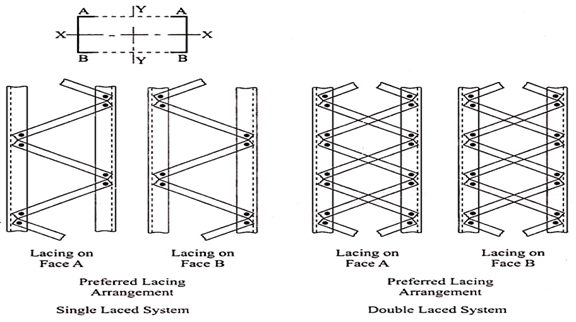
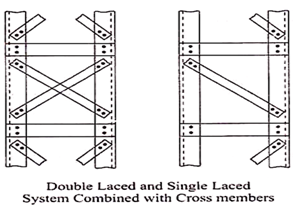
General Requirements for Lacing (IS 800):
(i) Compression members comprising two main components laced and tied, should where practicable have a radius of gyration about the axis perpendicular to the plane of lacing not less than the radius of gyration about the axis parallel to the plane of lacing.
(ii) As far as possible the lacing system shall be uniform throughout the length of the column.
(iii) Single laced systems on opposite faces of the components being laced together shall preferably be in the same direction so that one is the shadow of the other instead of being mutually opposed in direction.
(iv) The effective slenderness ratio (KL/r) e of laced columns shall be taken as 1.05 times the (KL/r) o, the actual maximum slenderness ratio, in order to account for shear deformation effects.
(v) Width of lacing bars – In bolted/riveted construction, the minimum width of lacing bars shall be three times the nominal diameter of the end bolt/rivet.
(vi) Thickness of lacing bars – The thickness of flat lacing bars shall not be less than one-fortieth of its effective length for single lacing and one-sixtieth of the effective length for double lacings.
(vii) Rolled sections or tubes of equivalent strength may be permitted instead of flats for lacings.
(viii) Angles of inclination – Lacing bars, whether in double or single or double system shall be inclined at an angle not less than 40° nor more than 70° to the axis of the built-up member.
(ix) Spacing – The maximum spacing of lacing bars, whether connected by bolting, riveting or welding, shall also be such that the maximum slenderness ratio of the components of the main member (a1/r1) between consecutive lacing connections is not greater than 50 or 0.7 times the most unfavourable slenderness ratio of the member as a whole, whichever is less, where a1 is the unsupported length of the individual member between lacing points, and r1 is the minimum radius of gyration of the individual member being laced together.
Design of Lacings:
The lacing shall be proportioned to resist a total transverse shear Vt, at any point in the member, equal to at least 2.5 per cent of the axial force in the member and shall be divided equally among all transverse lacing systems in parallel planes.
Key takeaways:
- As far as possible the lacing system shall be uniform throughout the length of the column.
- Single laced systems on opposite faces of the components being laced together shall preferably be in the same direction so that one is the shadow of the other instead of being mutually opposed in direction.
- The effective slenderness ratio (KL/r) e of laced columns shall be taken as 1.05 times the (KL/r) o, the actual maximum slenderness ratio, in order to account for shear deformation effects.
- Width of lacing bars – In bolted/riveted construction, the minimum width of lacing bars shall be three times the nominal diameter of the end bolt/rivet.
Compression members composed of two main components battened should preferably have the individual members of the same cross-section and symmetrically disposed about their major axis.
Where practicable, the compression members should have a radius of gyration about the axis perpendicular to the plane of the batten not less than the radius of gyration about the axis parallel to the plane of the batten.
The battens should be placed opposite to each end of the member and at points where the member is stayed in its length and as far as practicable, be spaced and proportioned uniformly throughout.
The number of battens shall be such that the member is divided into not less than three bays within its actual length from center to center of end connections.
The effective slenderness ratio (KL/r) c of battened columns, shall be taken as 1.1-time (KL/r) o, the maximum actual slenderness ratio of the column, to account for shear deformation effects.
Design of Battens:
Battens shall be designed to carry the bending moments and shear forces arising from transverse shear force Vt equal to 2.5 per cent of the total axial force in the whole compression member, at any point in the length of the member divided equally between parallel planes of the battens.
Battened member divided equally between parallel planes of the battens.
Battened member carrying calculated bending moment due to eccentricity of axial loading, calculated end moments or lateral loads parallel to the plane of battens, shall be designed to carry actual shear in addition to the above shear.
The main members shall also be checked for the same shear force and bending moments as for the battens.
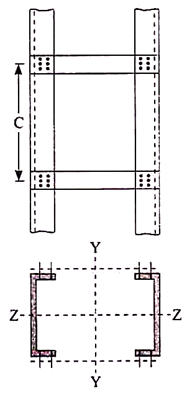
Battens shall be of plates, angles, channels or I-sections and at their ends shall be riveted, bolted or welded to the main components so as to resist simultaneously a shear Vb = (V1C)/N5 along the column axis and a moment M = (V1C)/2N at each connection.
Where,
V1 = Transverse shear force as defined above
C = Distance between center to center of battens, longitudinally
N = Number of parallel planes of battens, and
S = Minimum transverse distance between the centroid of the rivet/bolt group/welding connecting the batten to the main member.
Tie Plates:
Tie plates are members provided at the end of battened and laced members, and shall be designed by the same method as battens. In no case shall a tie plate and its fastening be incapable of carrying the forces for which the lacing or batten has been designed.
Size:
When plates are used for battens, the end battens and those at points where the member is stayed in its length shall have an effective depth, longitudinally, not less than the perpendicular distance between the centroids of the main members.
The intermediate battens shall have an effective depth of not less than three quarters of this distance, but in no case shall the effective depth of any batten be less than twice the width of one member in the plane of the battens.
The effective depth of a batten shall be taken as the longitudinal distance between outermost bolts, rivets or welds at the ends. The thickness of batten or the tie plates shall be not less than one-fiftieth of the distance between the innermost connecting lines of rivets, bolts or welds, perpendicular to the main member.
The requirement of bolt size and thickness of batten specified above does not apply when angles, channels or I-sections are used for battens with their legs or flanges perpendicular to the main member. However, it should be ensured that the ends of the compression members are tied to achieve rigidity.
Spacing of Battens:
In battened compression members where the individual members are not specifically checked for shear stress and bending moments, the spacing of battens, center to center of its end fastenings shall be such that the slenderness ratio (KL/r) of any component over that distance shall be neither greater than 50 nor greater than 0.7 times the slenderness ratio of the member as a whole about its Z-Z (axis parallel to the battens).
Key takeaways:
- The battens should be placed opposite to each end of the member and at points where the member is stayed in its length and as far as practicable, be spaced and proportioned uniformly throughout.
- The number of battens shall be such that the member is divided into not less than three bays within its actual length from center to center of end connections.
- The effective slenderness ratio (KL/r) c of battened columns shall be taken as 1.1-time (KL/r) o, the maximum actual slenderness ratio of the column, to account for shear deformation effects.
Compression Member Composed of Two Components Back‐to‐Back
Compression individuals composed of angles, channels, or tees lower back-to-lower back in touch or separated through a small distance will be related collectively through riveting, bolting or welding in order that the ratio of slenderness of every member among the connections isn't always extra than forty or extra than 0.6 instances the maximum destructive ratio of slenderness of the strut as a whole, whichever is much less
In no case shall the ends of the strut be related collectively with much less than rivets or bolts or their equal in welding, and there will be now no longer much less than extra connections in among, spaced equidistant alongside the duration of the strut. Where the individuals are separated lower back-to-lower back, the rivets or bolts via those connections shall by skip via stable washers or pickings. Where the legs of the related angles or the related tees are one hundred twenty-five mm extensive or more, or in which webs of channels are one hundred fifty mm extensive or over, now no longer much less than rivets or bolts will be utilized in every connection, one on-line of every gauge mark.
Where those connections are made through welding, stable packings will be used to impact the jointing except the individuals are sufficiently near collectively to allow direct welding, and the individuals will be related through welding alongside each pair of edges of the primary additives.
The rivets, bolts or welds in those connections will be enough to hold the shear pressure and moments, if any, targeted for battened struts and in no case shall the rivets or bolts be much less than sixteen mm diameter for individuals up to and inclusive of 10 mm thick; 20 mm diameter for individuals up to and inclusive of sixteen mm thick; and 22 mm diameter for individuals over sixteen mm thick.
Compression individuals related through such riveting, bolting or welding shall now no longer be subjected to transverse loading in an aircraft perpendicular to the riveted, bolted or welded surfaces.
Where the additives are in touch lower back-to-lower back, the spacing of the rivets, bolts or intermittent welds shall now no longer exceed the most spacing for compression individuals.
Key takeaways:
i) In no case shall the ends of the strut be related collectively with much less than rivets or bolts or their equal in welding, and there will be now no longer much less than extra connections in among, spaced equidistant alongside the duration of the strut.
Ii) Where the individuals are separated lower back-to-lower back, the rivets or bolts via those connections shall by skip via stable washers or pickings.
Iii) Where the legs of the related angles or the related tees are one hundred twenty-five mm extensive or more, or in which webs of channels are one hundred fifty mm extensive or over, now no longer much less than rivets or bolts will be utilized in every connection, one on-line of every gauge mark.
When rolled metallic column sections are to be had in lengths much less than the desired lengths, it is going to be important to offer splicing.
Sometimes the dimensions of the column for a higher ground can be much less than the dimensions of the column for the decrease ground.
In such instances additionally at sections wherein the cross-phase of the column adjustments suddenly, it is going to be important to offer splicing
Splicing includes connection of the 2 additives of a column via way of means of connecting plates. Where the ends of the compression participants are confronted for bearing, they will be spliced to preserve the related participants as it should be in role and to face up to any anxiety whilst bending is present. The ends of compression participants confronted for bearing shall always be machined to make certain ideal touch of surfaces in bearing.
Where such contributors aren't confronted for entire bearing the splices will be designed to transmit all of the forces to which they're subjected to. Where ever viable, splices will be proportioned and organized so that, the relevant axis of the splice coincides as almost as viable with the centroidal axes of the contributors joined on the way to keep away from eccentricity, however wherein eccentricity is gift within side the joint, the ensuing pressure be furnished for.
Types of Column Splices: The following kinds of column splices are used:
i) Splices for Axial Load: These are splices to switch axial hundreds from one column to the other. These splices include plates supplied over the flanges of the columns.
Ii) Splices for Moments: When splices are predicted to withstand a bending moment, then such splices are supplied within side the shape of plates over the flanges of columns. These splices are known as flange splices. In this case, the splices are designed deliberating the direct load to be transmitted in addition to the bending moment.
Iii) Splices for Horizontal Shear: Splices intended to withstand horizontal shear are supplied within side the shape of plates over the webs of the columns. Such splices are known as internet splices.
Key takeaways:
i) When rolled metallic column sections are to be had in lengths much less than the desired lengths, it is going to be important to offer splicing.
Ii) Sometimes the dimensions of the column for a higher ground can be much less than the dimensions of the column for the decrease ground.
Iii) In such instances additionally at sections wherein the cross-phase of the column adjustments suddenly, it is going to be important to offer splicing
The columns are supported at the column bases. The column bases transmit the column load to the concrete or masonry basis blocks.
The column load is unfolded over massive location on concrete or masonry blocks. The depth of bearing stress on concrete or masonry is stored inside the most permissible bearing stress.
The protection of the shape relies upon up on balance of basis. The column bases need to be designed with utmost care and skill. In the column bases, depth of stress on concrete block is thought to be uniform.
The column bases will be of ok strength, stiffness and location to unfold the burden upon the concrete, masonry, different basis or different helps without exceeding the allowable strain on such basis below any mixture of the burden and bending moments.
The column bases are of types;
- Slab base
- Gusseted bases
- Slab base
The column give up is confronted for bearing over the complete area. The gussets (gusset plates and gusset angles) aren't supplied with the column with slab bases. The enough fastenings are used to hold the elements securely in plate and to withstand all moments and forces, apart from the direct compression. The forces and moments springing up all through transit, unloading and erection also are considered. When the slab by myself distributes the weight uniformly the minimal thickness of a square slab is derived as below;
Procedure
Step 1) Assume a suitable grade of concrete. Depending upon the grade of concrete used bearing strength of concrete is determine by 0.45fck
Step 2) The area of a slab base may be computed by
A= P/ bearing strength of concrete
Where,
A= area of base plate
P= Factored load
Step 3) A square base plate is generally provided. The side of the base plate may be worked out
L= B=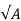 
Some designer feels that the projections of the base plate beyond column edges a and b are kept equal and these sides can be work out.
Using
(D+2b) x (bf+2a) = A
Where,
L= length of base plate in mm
B= width of base plate in mm
D= depth of column section in mm
Step 4) The intensity of pressure w from the concrete pedestal is determine by
W= P/A1
Where, w= intensity of pressure from concrete under the slab base
A1= Area of base plate provided in mm2
Step 5) The minimum thickness ts of the base plate is calculated by using
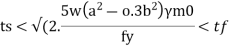
Step 6) Holding down bolts 2 or 4 in number and of 20 mm diameter are usually provided. When the base subjected to only axial compressive load two bolt will be enough.
Step 7) welded joint between the column and base plate is designed.
Step 8) Detailing
2. Gusseted base
Procedure
Step 1) Bearing strength of concrete is determined = 0.45 f
Step 2) Area of the base plate may be computed by,
A = P/0.45 fck
Step 3) The size of gusset base assumed
(i) Thickness: For bolted gusset base t <16 mm.
(ii) The gusset angle is chosen so as to accommodate two rows of bolts in the vertical leg and one row of bolt in the horizontal leg. Therefore, an unequal angle section is provided.
(iii) The thickness of gusset angle should be same as thickness of gusset plate.
(iv) Width of base plate.
L = depth of section + 2 (thickness of gusset plate +
Leg length of angle + over hang) (for bolted connections)
L = depth of section + 2x (thickness of gusset plate + overhang)
(For welded connections)
(v) Width of base plate
B = A/L
Step 4) The intensity of bearing pressure
W = P/A1
Where
A₁ = Area of base plate provided
Step 5) The thickness of the base plate is computed by equating the moment at the critical section to the moment of resistance of the gusset at that section.
B.M. At critical section
M = wc12/2(considering unit width)
Where
c.- Minimum over hang
Design bending moment at critical section M, 12
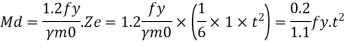
Now equating, M = Md
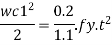
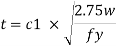
Where,
t= Total thickness including thickness of base plate and gusset angle (for bolted gusset base)
= Thickness of base plates (for welded gusset base)
W= Intensity of pressure from concrete under the slab faze.
C₁=Cantilever portion of base plate
Step 6) Holding down bolts 2 or 4 in numbers and of 20 diameter are usually provided.
Step 7) Design connection
Step 8) Detailing
Key takeaways:
Step 1) Assume a suitable grade of concrete. Depending upon the grade of concrete used bearing strength of concrete is determine by 0.45fck
Step 2) The area of a slab base may be computed by
A= P/ bearing strength of concrete
Step 3) A square base plate is generally provided. The side of the base plate may be worked out
L= B=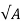 
Step 4) The intensity of pressure w from the concrete pedestal is determine by
W= P/A1
Step 5) The minimum thickness ts of the base plate is calculated by using
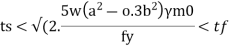
Step 6) Holding down bolts 2 or 4 in number and of 20 mm diameter are usually provided. When the base subjected to only axial compressive load two bolt will be enough.
Step 7) welded joint between the column and base plate is designed.
Step 8) Detailing
References:
- Design of Steel Structures by N. Subramanian, Oxford University Press
- Limit State Design of Steel Structures by S. K. Duggal, Tata McGraw Hill.
- Design of Steel Structures by K S Sairam, Pearson Education
- Design of Steel Structures by S Ramamurtham, DhanpatRai Publishing Company.
- Steel Structures by Robert Englekirk. Hohn Wiley & sons inc.
- Structural Steel Design by Lambert tall (Ronald Press Comp. Newyork.
- Design of steel structures by Willam T Segui, CENGAGE Learning
- Structural Steel Design By D MacLaughlin, CENGAGE Learning
