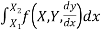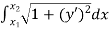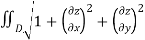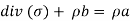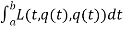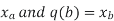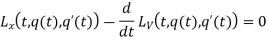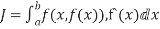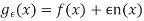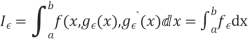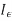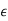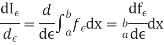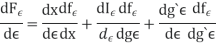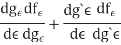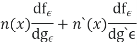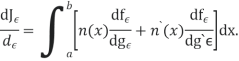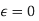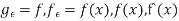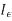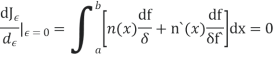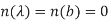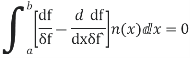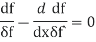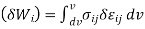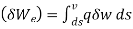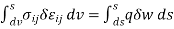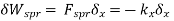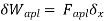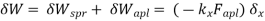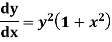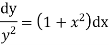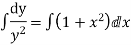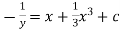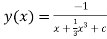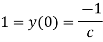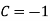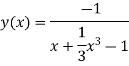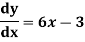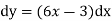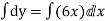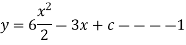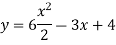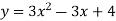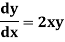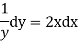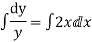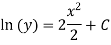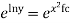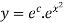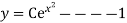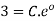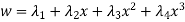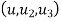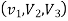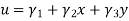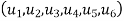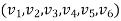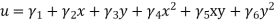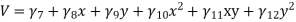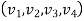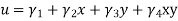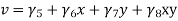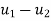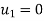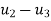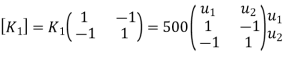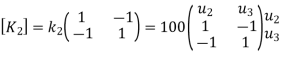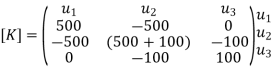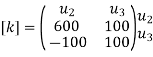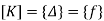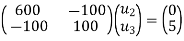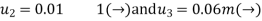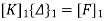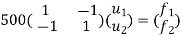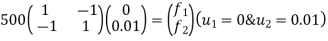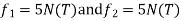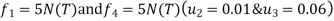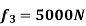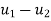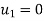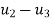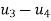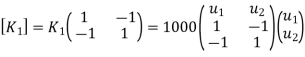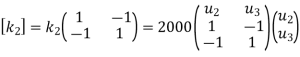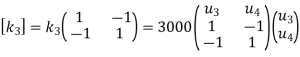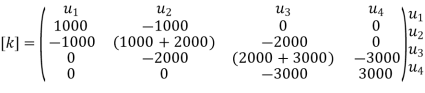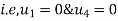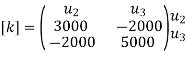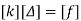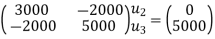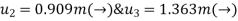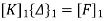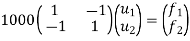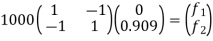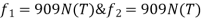UNIT-1
Calculus of variation
- The definite integral
I(y)=
|
Is a well-defined quantity.
a) When the integrated f is given as a function of X,Y,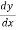 .
.
b) When y is a given function of x
c) And is a number, when x1 and x2 have definite numerical values.
- The first problem of calculus of variation involves comparison of the various values assumed by (1) when different choices of y as a function of x are substituted into the integrand of (1).
- What we want is to find the particular function y=y(x) that gives to (1) its minimum or maximum value.
- In calculus of variations, we will discuss these kind of problems in details. These includes the problems of
a) The shortest distance between two points on a given surface.
b) The quickest distance between two points.
c) The surface of revolution of minimum area,etc.
- The techniques of solving the problems of minimizing (or maximizing)of (1) and related definite integrals are closely connected with the problems of maxima and minima in the elementary differential calculus.
- A mapping which assigns a definite (real) numbers to each function belonging to the same class is called functional. Thus, we can say that a functional is a kind of function, where the independent variable is itself a function or a curve.
- Functionals are often expressed as definite integrals involving functions and their derivatives.Functionals play an important role in many problems in analysis , mechanics, geometry ,etc.
- For example, the arc length L of a plane curve y(x) connecting two given points (x1,y1) and (x2,y2) is a functional.
The quantity L may be computed as
L[y(x)]= |
- The area S of a surface bounded by a given curve C is also a functional and since this area is determined by the choice of surface z=z(x,y) so area S is given by
S[z(x,y)] = |
Here, D is the projection of the area bounded by the curve C on the xy- plane
- The branch of calculus of functionals in which we find the maxima and minima of the functionals is called the “calculus of variations”.Thus the calculus of variations investigates method that permit finding maximal and minimal values of functionals
- And the problems in which we investigate a functional for a maximum or a minimum are called variational problems.
- Equilibrium equations are Newton’s second law which states that the rate of change of linear momentum would be equal in magnitude and direction to the net applied force.
- Deformable bodies are subjected to two kinds of forces, namely, contact force and body force. As the name suggest the contact force arises by virtue of the body being in contact with its surroundings.
- Traction arises only due to these contact force and hence so does the stress tensor. The magnitude of the contact force depends on the contact area between the body and its surroundings.
- On the other hand, the body forces are action at a distance forces. Examples of body force are gravitational force, electromagnetic force. The magnitude of these body forces depend on the mass of the body and hence are generally expressed as per unit mass of the body and denoted by b.
- On further assuming that the Newton’s second law holds for any subpart of the body and that the stress field is continuously differentiable within the body the equilibrium equations can be written as:
|
Where, ρ is the density, a is the acceleration and the mass is assumed to be conserved.
- Also, the rate of change of angular momentum must be equal to the net applied moment on the body.
- Assuming that the moment is generated only by the contact forces and body forces, this condition requires that the Cauchy stress tensor to be symmetric. That is in the absence of body couples, σ = σt, where the superscript (⋅)t denotes the transpose.
- In the calculus of variations, the Euler equation is a second-order partial differential equation whose solutions are the functions for which a given functional is stationary. It was developed by Swiss mathematician Leonhard Euler and Italian mathematician Joseph-Louis Lagrange in the 1750s.
- Because a differentiable functional is stationary at its local extrema, the Euler–Lagrange equation is useful for solving optimization problems in which, given some functional, one seeks the function minimizing or maximizing it.
- This is analogous to Fermat's theorem in calculus, stating that at any point where a differentiable function attains a local extremum its derivative is zero.
- In Lagrangian mechanics, according to Hamilton's principle of stationary action, the evolution of a physical system is described by the solutions to the Euler equation for the action of the system. In this context Euler equations are usually called Lagrange equations.
- In classical mechanics, it is equivalent to Newton's laws of motion, but it has the advantage that it takes the same form in any system of generalized coordinates, and it is better suited to generalizations. In classical field theory there is an analogous equation to calculate the dynamics of a field.
- The Euler–Lagrange equation is an equation satisfied by a function q of a real argument t, which is a stationary point of the functional
S(q) = Where, q is the function to be found: q:[a,b] t such that q is differentiable, q(a)=
|
- The Euler–Lagrange equation, then, is given by
|
Here 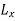
 and
and 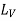 denote the partial derivatives of L with respect to the second and third arguments, respectively.
denote the partial derivatives of L with respect to the second and third arguments, respectively.
If the dimension of the space X is greater than 1, this is a system of differential equations, one for each component
- Derivation of the one-dimensional Euler – lagrange equation-
The derivation of the one – dimensional fuler-lagrange eq. is one of the classics proof in mathematics. We wish to find a function f which satisfies the boundary cond.
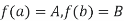 & which extremixes the functional.
& which extremixes the functional.
|
We assume that F is twice continuously differentiable A weaker assumption can be used but the proof becomes more difficult.
Let
|
i.e the result of such pertulation 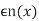 of f, where
of f, where 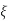 is small & n(x) is a differentiable function satisfying
is small & n(x) is a differentiable function satisfying 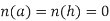
Then define,
We now wish to calculate the total derivative of
It follows from the total derivation that.
So,
Where &
Using the boundary conditions
Applying the fundamental lemma of calculus of variations now yields the Euler- Lagrange eq.
|
- When the force and displacement are unrelated to the cause and effect relation, the work is called as virtual work.
- Therefore, the virtual work may be caused by true force moving through imaginary displacements or vice – versa.
- Principle of virtual work stated that “A body is in equilibrium if the internal virtual work is equal to the external virtual work for every kinematical admissible displacements field. For the linear elasticity following equation is the principle of virtual work .
δWi= δWe Internal virtual work External virtual work
|
- In order to develop a number of powerful techniques based on a concept known as virtual work, imagine that the mass is not in fact at its equilibrium position but at an (incorrect) non-equilibrium position
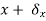 . The imaginary displacement
. The imaginary displacement 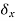 is called a virtual displacement.
is called a virtual displacement. - The virtual work
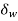 done by a force to be the equilibrium force times this small imaginary displacement
done by a force to be the equilibrium force times this small imaginary displacement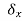 . It should be emphasized that virtual work is not real work – no work has been performed since x is not a real displacement which has taken place; this is more like a “thought experiment”.
. It should be emphasized that virtual work is not real work – no work has been performed since x is not a real displacement which has taken place; this is more like a “thought experiment”.
The virtual work of the spring force is then
The virtual work of the applied force is
The total virtual work is
|
- There are two ways of viewing this expression. First, if the system is in equilibrium
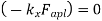 then the virtual work is zero,
then the virtual work is zero, 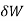 0.
0. - Alternatively, if the virtual work is zero then, since
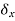 is arbitrary, the system must be in equilibrium. Thus the virtual work idea gives one an alternative means of determining whether a system is in equilibrium.
is arbitrary, the system must be in equilibrium. Thus the virtual work idea gives one an alternative means of determining whether a system is in equilibrium. - The symbol
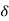 is called a variation so that, for example,
is called a variation so that, for example, 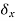 is a variation in the displacement (from equilibrium).
is a variation in the displacement (from equilibrium).
- The Principal of minimum potential energy stated that “for a conservative system for all kinematically admissible displacement fields those corresponding to equilibrium, extremes the total potential energy, if extreme condition is minimum, the equilibrium state is stable.
Π = U +V
Where,
Π=Total potential energy
U = strain energy (due to internal forces)
V= work potential (due to external forces)
U = ½ (σ) (ε) and V = -q w
|
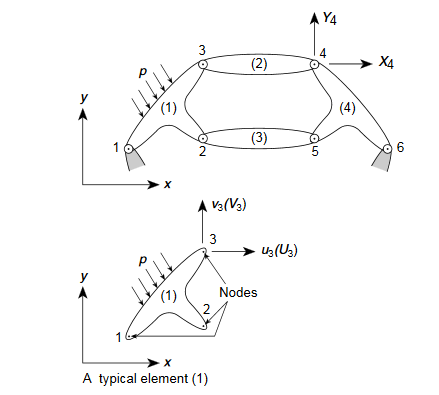
Fig .1 A typical structure built up from interconnected elements
- The system of equations resulting from Eq. Ku+ f= 0 can be solved once the prescribed support displacements have been substituted.
- In the example of Fig., where both components of displacement of nodes 1 and 6 are zero, this will mean the substitution of
u1=u6=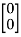
which is equivalent to reducing the number of equilibrium equations (in this instance 12) by deleting the first and last pairs and thus reducing the total number of unknown displacement components to eight. It is, nevertheless, often convenient to assemble the equation according to relation Ku+ f= 0. So as to include all the nodes.
- Clearly, without substitution of a minimum number of prescribed displacements to pre-vent rigid body movements of the structure, it is impossible to solve this system, because the displacements cannot be uniquely determined by the forces in such a situation.
- This physically obvious fact will be interpreted mathematically as the matrix K being singular,i.e., not possessing an inverse. The prescription of appropriate displacements after the assembly stage will permit a unique solution to be obtained by deleting appropriate rows and columns of the various matrices.
- If all the equations of a system are assembled, their form is
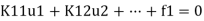
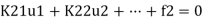
and it will be noted that if any displacement, such as u1= ̄u1, is prescribed then the total ‘force’ f1 cannot be simultaneously specified and remains unknown.
- The first equation could then be deleted and substitution of known values ̄u1 made in the remaining equations.
- When all the boundary conditions are inserted the equations of the system can be solved for the unknown nodal displacements and the internal forces in each element obtained.
Example -1
Solve the initial value problem.
|
With initial value y(0)=1
Solution-
Our ODF is sepretable , thus we, seprate
Now, integrable both sides we get,
Thus , So, Applying y© =1 we obtained
Finally,
|
Example 2
solve the initial value problem .
|
With initial value y(0)=4
Ans-
We are seprating our differential eq.
Applying y(x)=4 4=0-0+C C=4 Put this value in eq. 1
|
Example -3
solve the initial value problem
|
With initial value y(0)=3
Ans-
We are seperating our differential equation
Integrating both sides
Apply boundary value conditions Y(0)=3 Take exponential function both sides
C=3 Put in eq. 1
|
- We propose a flexibility-based finite element formulation for beams with stochastic bending stiffness. We formulate the element-level finite element equilibrium equation in terms of the element flexibility, so that the stochasticity appears on the right side of the equilibrium equation as the random flexibility.
- As a result, the unknown internal forces, which are dependent on the stochastic bending stiffness for statically indeterminate beams, appear explicitly in the global finite element equilibrium equations.
- The internal forces associated with the mean stiffness are used to approximate the unknown internal forces in the process of computation.
- With the new formulation, the mean and covariance of the displacement for stochastic beams can be directly calculated in terms of mean and covariance function of the flexibility, which can be evaluated from one-dimensional probability density function and the correlation function of the stiffness by the Monte Carlo simulation.
- The numerical example is given to illustrate the advantages of the new formulation over the conventional perturbation solution.
Displacement function for variance element as follows.
- Two noded bar element (1D)
DoF per node=01 (u) Total DoF =02 Select two element from pascal triangle to write displacement function . select only x or y -co ordinates displacement function
|
2. Two noded beam element (1D) (bending moment)
Dof per node =02 Total Dof =04 Select four element from pascal triangle to write displacement function . select only x- co ordinate Displacement function =
|
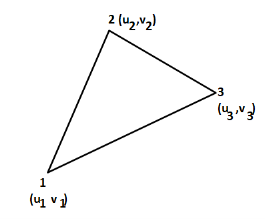
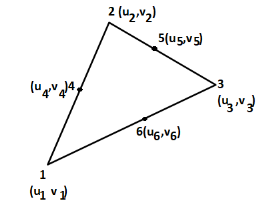
3. Three noded triangle (CST) element (2D)
DoF per node =02 (U,V) Total Dof =06 03 DoF in x-dim 03 DoF in y – dim Select three element from pascal triangle to write displacement function. Since it is 2D element , select x& y coordinates both. Displacement function =
|
4. Six noded triangular (LST) element (2D)
DOf per node =02 (U,V) Total Dof =12 06 DoF in x-dim 06 Dof in y -dim Displacement function
|
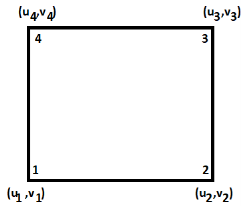
5. Four noded rectangular element (2D)
DOf per node =02 (U,V) Total Dof =08 06 DoF in x-dim 06 Dof in y -dim Displacement function
|
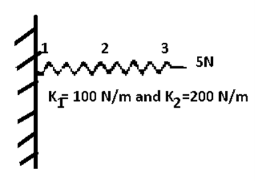
Example(1)
Determine elongations at each node and hence the forces in springs.
|
Solution –
discretizations
Element | K(N/m) | Nodes | Displacements m | boundary conditions |
1 | 500 | 1-2 |
|
|
2 | 100 | 2-3 |
| ----- |
Step -2
Element stiffness matrices.
|
Step -3 global stiffness matrix
Assemble the element stiffness matrices to get global stiffness matrix
|
Step -4
reduced stiffness matrix imposing boundary conditions i.e Therefore, reduced stiffness matrix is.
|
Step-5
determine unknown joint displacement Applying equation of equilibrium
|
Step -6
calculation of spring force. Spring -1
Spring 2 –
|
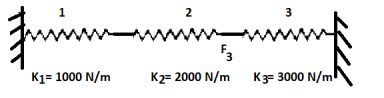
Example 2
Determine elongations at each node & hence the forces in springs
Take
|
Solution
Step-1 discretization
Element | K(N/m) | Nodes | Displacement | Boundary conditions |
1 | 1000 | 1-2 |
|
|
2 | 2000 | 2-3 |
| - |
3 | 3000 | 3-4 |
|
|
Step -2
element stiffness matrices
|
Step -3
global stiffness matrix Assemble the element stiffness matrices to get the global stiffness matrix
|
Step -4
reduced stiffness matrix Imposing boundary conditions
Eliminate first raw, first column & fourth raw & fourth column . Therefore reduced stiffness matrix is
|
Step -5
determine unknown joint displacement Applying equation of equilibrium
|
Step -6
calculate of spring force Spring 1 -
|
References:
1. Concepts and Applications of Finite Element Analysis: COOK. D. Robert. Malus.S.David, Plesha E. Michel, John wilely & sons 3rd Edn. New York, 2000
2. Finite Element Analysis -C.S. Krishnanmoorthy, Tata McGraw Hill Publishing Co. Ltd, New Delhi,
3. Introduction to the Finite Element method -Desai / ABEL-C.B.S. Publishers & Distributors, New Delhi.