Module-3
Formal logic, group, ring, and field
A proposition (or statement) is a declarative statement that is true or false, but not both.
Example-
(i) Ice floats in water.
(ii) China is in Europe
(iii) 2 + 2 = 4
(iv) 2 + 2 = 5
Compound proposition-
Many propositions are composite, that is, composed of sub-propositions and various connectives discussed
Subsequently, such composite propositions are called compound Propositions.
A proposition is said to be primitive if it cannot be broken down into simpler propositions, that is if it is not composite.
The following two propositions are composite:
“Roses are red and violets are blue.” and “John is smart or he studies every night.”
Basic logical operations-
1. Conjunction- p ⋀ q
Any two propositions can be combined by the word “and” to form a compound proposition called the conjunction of the original propositions. Symbolically,
P ∧ q
Read “p and q, ” denotes the conjunction of p and q. Since p ∧q is a proposition it has a truth value and this truth
Value depends only on the truth values of p and q.
Note- If p and q are true, then p ∧q is true; otherwise, p ∧q is false.
2. Disjunction, p ∨q
Any two propositions can be combined by the word “or” to form a compound proposition called the disjunction of the original propositions. Symbolically,
p∨q
Read “p or q, ” denotes the disjunction of p and q. The truth value of p ∨q depends only on the truth values of p
And q as follows-
If p and q are false, then p ∨q is false; otherwise, p ∨q is true
Negation-
Given any proposition p, another proposition, called the negation of p, can be formed by writing “It is not true that . . .” or “It is false that . . .” before p or, if possible, by inserting in p the word “not.” Symbolically, the negation of p, read “not p, ” is denoted by
¬p
The truth value of ¬p depends on the truth value of p as follows-
If p is true, then ¬p is false; and if p is false, then ¬p is true
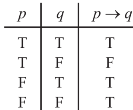
Conditional and bi-conditional statement-
The statements are of the form “if p then q”. Such statements are called conditional statement and these are denoted by-
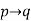
We read it as p implies q.
And another statement is of the form “p if and only if q”, such statement are called bi-conditional statement and it is denoted by-
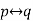
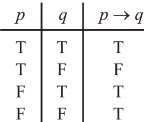
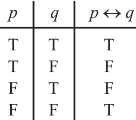
The truth value for conditional and bi-conditional value are given in the following tables-
Example: write the disjunction of- clothes are red. Violets are blue.
Sol.
Suppose p: clothes are red
q: violets are blue,
Then the disjunction of p and q can be written as-
p ∨ q: clothes are red or violets are blue.
Example: Construct the truth table for p ∨ 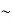 q.
q.
Sol.
p | Q | 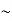 | p ∨ 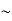 |
T | T | F | T |
T | F | T | T |
F | T | F | F |
F | F | T | T |
Example: Construct the truth table for 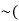 p ∨ q).
p ∨ q).
Sol.
p | Q | 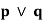 | 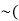 |
T | T | T | F |
T | F | T | F |
F | T | T | F |
F | F | F | T |
Logical connectives-
The word like ‘not’, ‘and’ etc. are known as logical connectives.
These are used to connect the statements.
The common connectives are- negation (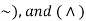 or
or 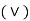 , if... Then (
, if... Then (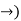 , if and only if
, if and only if 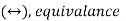
A statement formula that is true for all possible values of its propositional variables is called a Tautology.
Ex.- 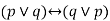 is a tautology
is a tautology
Contradiction-
Similarly, a proposition that is false for all possible truth values of the simple propositions that constitute it is called a contradiction.
Consistency-
A statement formula that can either be true or false depending upon the truth values of its propositional variables is called a contingency.
Example-
(p ∨ q) ↔(q ∨p) is a tautology.
Example-
p∨~p is a tautology.
Example- Show that p ∨~p is a tautology.
Solution: First we will construct the truth table for (p ∨~p)
p | 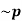 | (p ∨~p) |
T | F | T |
T | T | T |
p∨~p is always true.
Hence p ∨~p is a tautology.
Example:
Show that (p ∧q) →p is a tautology.
Solution: Let us construct the truth table for the statement (p ∧q) →p
p | Q | p ∧q | (p ∧q) →p |
T | T | T | T |
T | F | F | T |
F | T | F | T |
F | F | F | T |
Here 4th column has T entries then (p ∧q) →p is a tautology.
Example:
Verify that p ∧q ∧~ p is a contradiction and p →q ↔~ p ∨q is a tautology.
Solution: Let us draw the truth tables of these two propositions-

Looking at the fifth column of the table, you can see that p ∧q ∧~p is a contradiction.
p→q ↔~ p ∨q is a tautology
Example: Show that
((p ∨~q) ∧(~p ∨~q)) ∨q is a tautology.
Solution: Consider
((p ∨~q) ∧(~p ∨~q)) ∨q
≡((p ∨~q) ∧~p ∨(p ∨~q) ∧~q) ∨q
≡((p ∧~p) ∨(~q ∧~p) ∨(p ∧~q) ∨(~q ∧~q)) ∨q
≡(f ∨(~q ∧~p) ∨(p ∧~q) ∨~q) ∨q
≡(~ q ∧~p) ∨(p ∧~q) ∨~q ∨q
≡(~ q ∧~p) ∨(p ∧~q) ∨t(Since ~q ∨q ≡t)
≡ t
Hence ((p ∨~q) ∧(~p ∨~q)) ∨q is a tautology.
Laws of logic-
1. Idempotent Laws:
(a) p∨p ≡p (b) p ∧p ≡p
2. Commutative Laws:
(a) p∨p ≡q ∨p (b) p ∧q ≡q ∧p
3. Associative Laws:
(a) (p∨q) ∨r ≡p ∨(q ∨r) (b) (p ∧q) ∧r ≡p ∧(q ∧r)
4. Distributive Laws:
(a) p∨(q ∧r) ≡(p ∨q) ∧(p ∨r)
(b) p∧(q ∨r) ≡(p ∨q) ∨(p ∧r)
5. Identity Laws:
(a) (i) p ∨f ≡p (ii) p ∨t ≡t
(b) (i) p ∧f ≡f (ii) p ∧t ≡p
6. Complement Laws:
(a) (i) p ∧~p ≡t (ii) p ∧~p ≡f
(b) (i) ~~p ≡p (ii) ~t ≡f, ~ f ≡t
7. De Morgan’s Laws:
(a) ~(p ∨q) ≡~p ∧~q (b) ~(p ∧q) ≡~p ∨~q
Here t and f are used to denote the variables which are restricted to the truth values true and false respectively.
Duality law
Two statement formulas P and P* are said to be duals of each other if either one can be obtained from the other by replacing ∧and ∨and ∨ by ∧.
Tautological implications
A proposition P (p1, p2, ...) is said to logically imply a proposition Q ( p1, p2, ...) if one of the conditions in Theorem 1.1 holds.
If P (p1, p2, ...) logically implies Q ( p1, p2, ...) then we symbolically denote it by writing
P ( p1, p2, ...) ⇒Q ( p1, p2, ...)
Example- (p →q) ∧(q →r) →(p →r) is a tautology.
Hence (p →q) ∧(q →r) ⇒(p →r)
Logical implications-
A proposition P(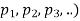 is said to logically imply a proposition Q(
is said to logically imply a proposition Q(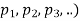 if it satisfies one of the following conditions-
if it satisfies one of the following conditions-
Where P(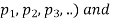 Q(
Q(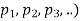 are two propositions.
are two propositions.
There are the following conditions-
- P(
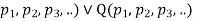 is a tautology.
is a tautology. - P(
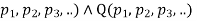 is a contradiction.
is a contradiction. - P(
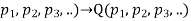 is a tautology.
is a tautology.
Note- the relationship in proposition defined by-
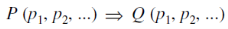
Is transitive, reflexive, and anti-symmetric.
Disjunctive normal form-
Definition-
Suppose A denotes a given formula. Another formula B which is equivalent to A will be called a disjunctive normal form of A if B is a sum of elementary products.
A disjunctive normal form of a given formula is constructed as given below-
(i) Replace ‘→’, ‘↔’ by using the logical connectives ∧, ∨and ~.
(ii) Use De Morgan’s laws to eliminate ~ before sums or products.
(iii) Apply distributive laws repeatedly and eliminate the product of variables to obtain the required normal form.
Example: Obtain disjunctive normal form ofp ∨(~p →(q ∨(q →~r)))
Solution: p ∨(~p →(q ∨(q →~r)))
≡p ∨(~p →q ∨(~q ∨~r)))
≡p∨(p ∨(q ∨(~q ∨~r)))
≡p∨p ∨q ∨~q ∨~r
≡p∨q ∨~q ∨~r
Therefore, the disjunctive normal form of
p∨(~p →(q ∨( ~q →~r))) is p ∨q ∨~q ~r
Example: Obtain the disjunctive normal form of
(a) p∨(~p →(q ∨(q →~r)))
Solution:
(a) p∨(_ p →(q ∨(q →_ r)))
≡p∨(_ p →q ∨(_ q ∨_ r))
≡p∨( p ∨q ∨(_ q ∨_ r))
≡p∨p ∨q ∨_ q ∨_ r
≡p∨q ∨_ q ∨_ r
Conjunctive normal form-
Let A denote a given formula, another formula B which is equivalent to A is called conjunctive normal formula if B is a product of an elementary sum.
Principal disjunctive normal form-
Definition 1.5: If A is a given formula, then an equivalent formula B, consisting of disjunctives of
Minterms only is called the Principal disjunctive normal form of the formula A.
Example: Obtain the principal disjunctive normal form of (~ p ∨~ q)→ (~ p ∧r ).
Solution: (~ p ∨~ q)→ (~ p ∧r )
⇔~(~ p ∨~ q) ∨ (~ p ∧r )
⇔~ (~(p ∧q)) ∨ (~ p ∧r )
⇔( p∧q) ∨ (~ p ∧r )
⇔( p∧q ∧ (r ∨~ r )) ∨ (~ p ∧r ∧ (q ∨~ q))
⇔( p∧q ∧r) ∨ ( p ∧q ∧~ r) ∨ (~ p ∧r ∧q) ∨ (~ p ∧r ∧~ q)
The principal disjunctive normal form of the given formula is
( p∧q ∧r) ∨( p∧q ∧~ r) ∨ (~ p ∧q ∧r) ∨ (~ p ∧~ q ∧r)
Example: Obtain the principal disjunctive normal form of ~p ∨q.
Solution: ~p ∨q ≡(~p ∧(q ∨~q)) ∨(q ∧(p ∨~p))
≡(~p ∧q) ∨(~p ∧~q) ∨(q ∧p) ∨(q ∧~p)
≡(~p ∧q) ∨(~p ∧~q) ∨(p ∧q)
Therefore (~p ∧q) ∧(~p ∧~q) ∧(p ∧q) is the required principal disjunctive normal form.
Principal conjunctive normal form-
Definition 1.6: If A is a given formula, then an equivalent formula B is called principle conjunctive normal form of Aif B is a product of max terms.
Theory of inference of statement calculus-
Modus ponens and modus tollens-
An argument form consisting of two premises and a conclusion is called a syllogism. The first and second premises are called the major premise and minor premise, respectively.
The most famous form of syllogism in logic is called modus ponens. It has the following form:
If p then q.
p
∴q
Example:
If the sum of the digits 469437 is divisible by 3
Then 469437 is divisible by 3.
Another valid argument form is called modus tollens.
Modus tollens means- method of denying.
It has the following form-
If p then q.
∼q
∴∼p
For example-
If Rahim is tall, then Rahim is thick.
Rahim is not thick.
∴Rahim is not tall.
Arguments –
An argument is an assertion that is given a set of prepositions 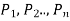 called premises, yields another preposition Q, called the conclusion.
called premises, yields another preposition Q, called the conclusion.
Such an argument is denoted by-

The notion of a “logical argument” is defined as follows-
The argument  is said to be valid if Q is true whenever all the premises
is said to be valid if Q is true whenever all the premises 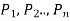 are true.
are true.
Note- An argument that is not valid is called a fallacy.
Example: the following argument is valid-
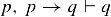
The proof of this rule follows from the truth table given below-
Consider an example-
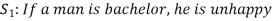
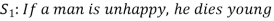
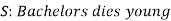
Here S denotes the conclusion of the argument and statements 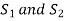 are the premises.
are the premises.
Here we claim the argument 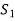 ,
, 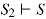 is valid
is valid
The rules of inference- (Modus ponens and modus tollens)
The theory of inference is a form of argument that is valid.
Modus ponens and modus tollens are both rules of inference.
The following results give the rules of inference-


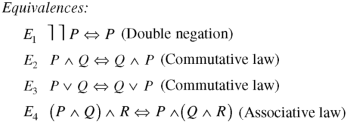

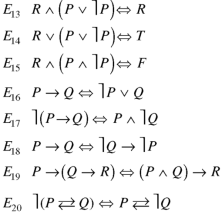
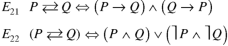
1. Modus ponens (Law of detachment)-
Let us consider the following argument-
If Ravi can fire, he will hit the target
Ravi can fire,
Therefore, he will hit the target.
To study the form of the argument, suppose p be the proposition ‘Ravi can fire’ and q be the proposition ‘ Ravi will hit the target’.
Then the premises are p→q and p.
The conclusion is q.
Hence the form of argument-
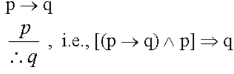
To check the validity of this argument we will construct a truth table as follows-
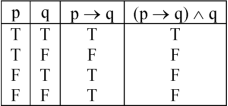
By looking at the second column(the conclusion) and the fourth column(the premises).
Whenever the premises are true in the first row the conclusion is true.
Hence the argument is valid.
This is the form of valid argument and this law is called the law of detachment because the conclusion q is detached from a premise.
We also call it the law of direct inference.
2. Modus tollens (Law of detachment)-
Let us consider the following argument-
If Ravi can fire, he will hit the target.
Ravi will not hit the target.
Therefore, Ravi cannot fire.
The argument is of the form-
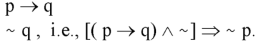
Semi-group-
Suppose * is the binary operation on S, where S is a non-empty set then the algebraic (S, *) is said to be a semigroup if the operation * is associative.
A semigroup has-
- A binary operation * defined on the elements of S.
- Closure, a * b whenever a, b
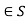 .
. - Associativity (a*b)*c = a*(b*c) for all a, b, c
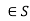
Homomorphism of semi-group-
Suppose there are two semi-groups (S, *) and (T, 0) then a mapping f: S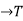 such that for any two elements a, b
such that for any two elements a, b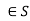
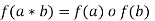
Is known as a semi-group homomorphism.
Isomorphism of semi-group-
Suppose there are two semi-groups (S, *) and (T, 0) then a mapping f: S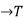 is called a semi-group isomorphism if f is onto and one-to-one.
is called a semi-group isomorphism if f is onto and one-to-one.
Monoids-
An algebraic system (M, *) is said to be monoid if-
- (a*b)*c = a*(b*c) for every for all a, b, c
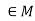 .
. - There exists an element e
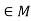 such that e*a = a*e = a for every for all a
such that e*a = a*e = a for every for all a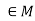
Example: Let Z be the set of integers (Z, +) is a monoid 0 is the identity element in Z with respect
To +.
Note-
A monoid is said to be cyclic if there exists an element a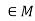 such that every element of M can be expressed as some power of a.
such that every element of M can be expressed as some power of a.
Monoid homomorphism-
Let (M, *) and (T, 0) be any two monoid demand denote the identity elements of
(M, *) and (T, 0) respectively. A mapping
f: M →T such that for any two elements a, b ∈M
f(a * b) = f (a) o f(b)
And
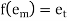
Is called a monoid homomorphism.
Group-
A group is an algebraic structure (G, *) in which the binary operation * on G satisfies the following conditions:
Condition-1: for all a, b, c, ∈G
a* (b * c) = (a * b) * c (associativity)
Condition-2:there exists an elements e ∈G such that for any a ∈G
a* e= e * a = a (existence of identity)
Condition-3: for every a ∈G, there exists an element denoted by 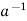 in G such that
in G such that
a* 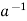 =
= 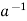 * a = e
* a = e
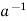 is called the inverse of a in G.
is called the inverse of a in G.
Example: (Z, +) is a group where Z denotes the set of integers.
Example: (R, +) is a group where R denotes the set of real numbers.
Abelian group-
Let (G, *) be a group. If * is commutative that is
a* b = b * a for all a, b ∈G then (G, *) is called an Abelian group.
Finite group-
A group G is said to be a finite group if the set G is a finite set.
Infinite group-
A group G, which is not finite is called an infinite group.
Order of a finite group-
The order of a finite group (G, *) is the number of distinct elements in G. The order of
G is denoted by O (G) or by |G|.
Example: If G = {1, -1, i, -i} where i= 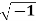 , then show that G is an abelian group with respect to multiplication as a binary operation.
, then show that G is an abelian group with respect to multiplication as a binary operation.
Sol.
First, we will construct a composition table-
. | 1 | -1 | I | -i |
1 | 1 | -1 | I | -i |
-1 | -1 | 1 | -i | i |
i | i | -i | -1 | 1 |
-i | -i | i | 1 | -1 |
It is clear from the above table that algebraic structure (G, .) is closed and satisfies the following conditions.
Associativity- For any three elements a, b, c ∈G (a ⋅b) ⋅c = a ⋅(b ⋅c)
Since
1 ⋅(−1 ⋅i) = 1 ⋅−i= −i
(1 ⋅−1) ⋅i= −1 ⋅i= −i
⇒1 ⋅(−1 ⋅i) = (1 ⋅−1) i
Similarly with any other three elements of G the properties holds.
∴Associative law holds in (G, ⋅)
Existence of identity: 1 is the identity element (G, ⋅) such that 1 ⋅a = a = a ⋅1 ∀a ∈G
Existence of inverse: 1 ⋅1 = 1 = 1 ⋅1 ⇒1 is inverse of 1
(−1) ⋅(−1) = 1 = (−1) ⋅(−1) ⇒–1 is the inverse of (–1)
i⋅(−i) = 1 = −i⋅i⇒–iis the inverse of iin G.
−i⋅i= 1 = i⋅(−i) ⇒iis the inverse of –iin G.
Hence inverse of every element in G exists.
Thus all the axioms of a group are satisfied.
Commutativity: a ⋅b = b ⋅a ∀a, b ∈G hold in G
1 ⋅1 = 1 = 1 ⋅1, −1 ⋅1 = −1 = 1 ⋅−1
i⋅1 = i= 1 ⋅i; i⋅−i= −i⋅i= 1 = 1 etc.
Commutative law is satisfied
Hence (G, ⋅) is an abelian group.
Example-
Prove that the set Z of all integers with binary operation * defined by a * b = a + b + 1 ∀a, b ∈G is an abelian group.
Sol: Sum of two integers is again an integer; therefore a +b ∈Z ∀a, b ∈Z
⇒a +b + 1 ⋅∈Z ∀a, b ∈Z
⇒Z is called with respect to *
Associative law for all a, b, a, b ∈G we have (a * b) * c = a * (b * c) as
(a* b) * c = (a + b + 1) * c
= a + b + 1 + c + 1
= a + b + c + 2
Also
a* (b * c) = a * (b + c + 1)
= a + b + c + 1 + 1
= a + b + c + 2
Hence (a * b) * c = a * (b * c) ∈a, b ∈Z.
Cosets-
Let (H, *) is a subgroup (G, *) and a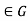
Then the sub-set-
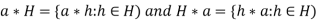
Are called left coset and right coset of H in G respectively.
Example- consider the group (Z, +)
And let
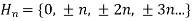
Then the left coset of H in Z are-
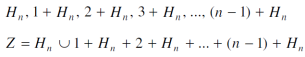
Note- if (H, *) is a subgroup of (G, *) then a*H = b*H iff 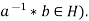
Theorem- if (H, *) is a subgroup of (G, *), then any two left coset of H in a are either identical or disjoint.
Proof:
Suppose a*H and b*H be two le cosets of H in G.
And if a*H and b*H have no common elements then a*H and b*H are disjoint.
If
a*H 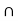 b*H
b*H 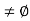
Let
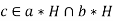
Then
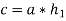 and
and 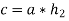
For some 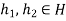
It will follow-
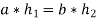
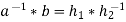
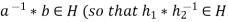 )
)
a * H 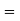 b * H
b * H
Lagrange’s theorem-
According to Lagrange’s theorem-
The order of any subgroup of a finite group divides the order of the group.
We will prove the theorem below-
Proof:
Suppose a finite group (G, *) of order h and (H, *) be a subgroup of G which has order m.
We can break the set G into a union of a finite number of distinct left cosets of H.
Let 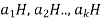 denotes the k distinct left cosets of H in G.
denotes the k distinct left cosets of H in G.
Such that-
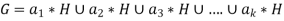
Note- all the K left cosest appearing on the right-hand side are disjoint.
So that-
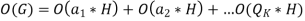
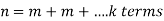
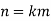
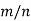
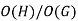
Which is the complete proof of Lagrange’s theorem.
Congruence relation-
“The relation congruence modulo ‘m’ is an equivalence relation in the set of integers. The operation ‘Congruence modulo m’ Partitions Z into disjoint equivalence classes called residue classes modulo m or congruence classes modulo m.”
Cyclic groups-
Suppose (G, *) is a group. If there exists an element 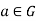 such that-
such that-
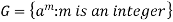
A group (G, *) is cyclic if there exists an element 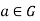 such that every element of G is a power of ‘a’ and ‘a’ is called the generator of a cyclic group.
such that every element of G is a power of ‘a’ and ‘a’ is called the generator of a cyclic group.
Note-
- Every cyclic group is abelian
- Every group of prime order is cyclic
- Every infinite cyclic group is isomorphic to (Z, +).
- Every proper sub-group of an infinite cyclic group is isomorphic to the group itself.
- Every proper sub-group of the finite cyclic group is a finite cyclic group
The only groups which do not possess proper sub-group are the prime order finite sub-groups.
Permutation group-
A permutation is a one-one mapping of a non-empty set onto itself.
Equal permutation-
The permutation f and G defined on S, (where S is a non-empty set) are said to be equal if f(a) = g(a) for all a which belong to S.
Example: let S = {a, b, c} and f = 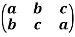
Here we can write-
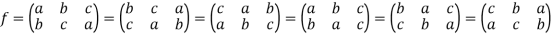
So that there are 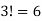 ways to write f.
ways to write f.
Product of permutations-
Suppose S = 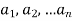 and let-
and let-
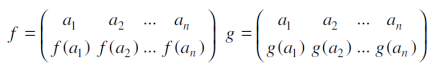
Be two arbitrary on S.
We find the composite of f and g as below-
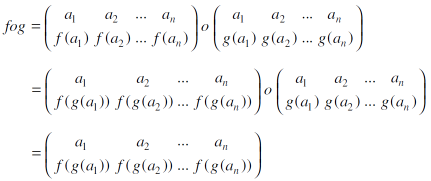
Example: let S = {a, b, c}
And 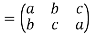 ,
, 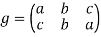 be the two permutations on S,
be the two permutations on S,
Then f o g-
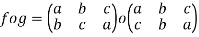
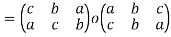
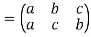
The inverse of a permutation-
Suppose f is a permutation on S = 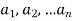 such that-
such that-
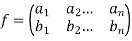
Then
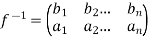
Elementary properties of groups-
- If (G, *) is a group, then the inverse of each element is unique.
Proof:
Suppose 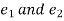 be the identity elements in G.
be the identity elements in G.
And let 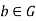 be an inverse of ‘a’ in G also let
be an inverse of ‘a’ in G also let 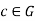 be an inverse of ‘a’ in G since b is the inverse of a,
be an inverse of ‘a’ in G since b is the inverse of a,
We get-
a * b = b * a = e
Also, c is an inverse of a in G 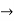 a* c = c * a = e
a* c = c * a = e
Now
b = b * e
= b * (a * c) (e is the identity)
= (b * a) * c
= e * c (by associative law)
= c
2. If (G, *) is a group, then the identity element in G is unique.
Proof:
Suppose 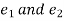 be the identity elements in G.
be the identity elements in G.
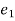 is the identity element and
is the identity element and 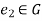
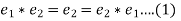
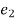 is the identity element and
is the identity element and 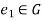
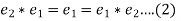
Now from equation (1) and (2), we get-
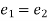
3. If (G, 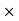 ) is a group, then-
) is a group, then-
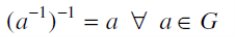
Proof:
If G is a group
Then 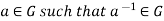
Such that-
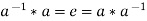
Now
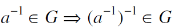
Such that-
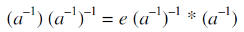
Let consider- 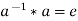
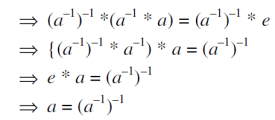
Therefore-
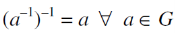
4. Cancellation laws hold good in G, which means-
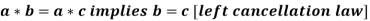
And
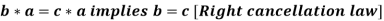
Proof:
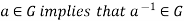 such that-
such that-
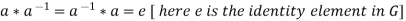
Now consider-
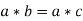
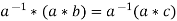
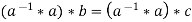
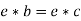
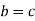
Now
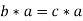
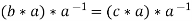
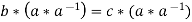
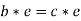
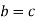
Therefore the cancellation laws hold good in group G.
Definition-
An algebraic system (R, +, .) is called a ring if the binary operations ‘+’ and ‘. ’ R satisfy the following conditions-
- (R, +) is an abelian group
- (R, .) is a semi-group.
- The operation ‘ .’ is distributive over +, that is for any, a, b, c belongs to R.
a .(b + c) = a . b + a . c
And
(b + c) . a = b. a + c. a
For example, the set of integers with respect to the operation + and 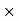 is a ring.
is a ring.
Some special types of rings-
- Abelian ring-
If a ring satisfies the commutative law then it is called an abelian ring.
2. Finite and infinite ring-
If the number of elements in a ring is finite it is called a finite ring otherwise it is called an infinite ring.
3. Ring with unity-
A ring that contains the multiplicative identity is called a ring with unity.
Order of a ring-
The order of a ring R is the number of elements in that ring.
It is denoted by |R|
Properties of a ring-
If R is ring then-
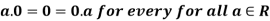
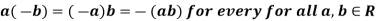
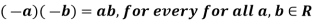
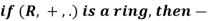 a.(b-c) = a.b – a.c
a.(b-c) = a.b – a.c
Note-
Let (R, +, .) be a ring, then R is said to be with zero divisors if there exist two non-zero elements 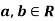 such that a. b = 0
such that a. b = 0
Sub-ring-
Let (R, +, .) be a ring and S be a non-empty subset of R. If (S, +, .) is a ring then
(S, +, .) is called a sub-ring of R.
Some important definitions-
Definition- Let (R, +, .) be a ring. If there exists a positive integer n such that na = 0 for all 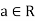 , then such a least positive integer n is called the characteristic of the ring R. If no such integer exists, then (R, +, .) is said to be characteristic zero.
, then such a least positive integer n is called the characteristic of the ring R. If no such integer exists, then (R, +, .) is said to be characteristic zero.
Definition- Let (R, +, .) be a ring. An element 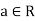 is said to be idempotent if a .a =
is said to be idempotent if a .a = 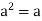
Definition- Let (R, +, .) be a ring. An element 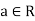 is said to be nilpotent if there exists a positive integer n such that
is said to be nilpotent if there exists a positive integer n such that 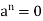
Definition- Let (R, +, .) be a ring. If a .a = a 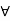
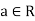 then (R, +, ⋅) is said to be a Boolean ring.
then (R, +, ⋅) is said to be a Boolean ring.
Definition- If (R, +, .) is a Boolean ring, then a + a = 0 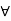
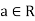
Field-
“A commutative division ring is called a field.”
Note-
- A finite integral domain is a field.
- The characteristic of the ring of integers (Z, +, .) is zero
- The characteristic of an integral domain is either a prime or zero.
- The characteristic of a field is either a prime or zero.
Reference Books
1. B.S. Grewal: Higher Engineering Mathematics; Khanna Publishers, New Delhi.
2. B.V. Ramana: Higher Engineering Mathematics; Tata McGraw- Hill Publishing Company Limited, New Delhi.
3. Peter V.O’ Neil. Advanced Engineering Mathematics, Thomas ( Cengage) Learning.
4. Kenneth H. Rosem: Discrete Mathematics its Application, with Combinatorics and Graph Theory; Tata McGraw- Hill Publishing Company Limited, New Delhi
5. K.D. Joshi: Foundation of Discrete Mathematics; New Age International (P) Limited,
Publisher, New Delhi.