Module-4
Set, Relation, function, and Counting Techniques
Sets- A set is a collection of well-defined objects which are called the elements or members of the set.
We generally use capital letters to denote sets and lowercase letters for elements.
If any element which exists in the set is to be denoted as-
Suppose an element ‘a’ is from a set X, then it is represented as- a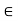
X
This means the element ‘a’ belongs to the set X.
If the element is not from the group then we use ‘not belongs to’.
Representation of sets-
There are two ways to represent sets.
1. In the first way, the elements of the set are separated by a comma and contained in the bracket-{ }.
2. The second way is that we define the characteristic of the element.
For example-
Suppose we have a set ‘A’ of all odd integers which are greater than 3.
Then we can represent it two ways-
1. A = {5, 7, 9…….}
2. A = {x | x is an odd integer, x>3 }
Subsets-
Let every element of set X is also an element of a set Y, then X is said to be the subset of Y.
Symbolically it is written as-
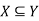
Which is read as- X is the subset of Y.
Note- If X = Y then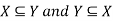 
Proper sub-set-
A set X is called a proper subset the set Y is-
1. X is a subset of Y
2. Y is not a subset of X
Note- every set is a subset to itself.
Equal sets-
If X and Y are two sets such that every element of X is an element of Y and every element of Y is an element of X, the set and set Y will be equal always.
We write it as X = Y and read as X and Y are identical.
Superset-
If X is a subset of Y, then Y is called a superset of X.
Null set-
A set that does not contain any element is known as the null set.
We denote a null set by ∅
The null set is a subset of every set.
Singleton-
A set that has only one element is called a singleton.
Example- A = {10} and B = {∅}
Theorem- if ∅ and ∅’ are empty sets then ∅=∅’
Proof: Let ∅≠ ∅’ then the following conditions must be true-
1. There is element x∈∅ such that x∉∅’
2. There is an element x∈∅’ such that x∉∅.
But both these conditions are false since ∅’ and ∅’ has any elements if follows that ∅=∅’.
Operations on sets-
1. Union and intersection-
Union-We denotes the union of two sets as- A∪B, which is the set of all elements which belong to A or B.
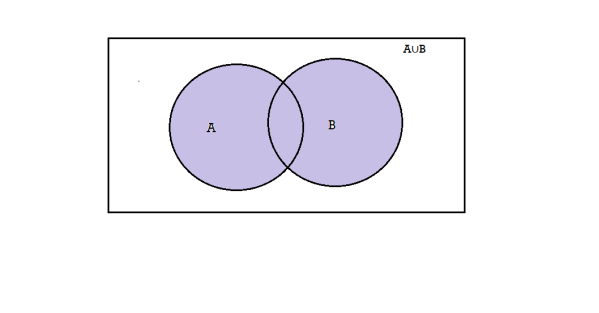
That is-
A∪B = {x |x∈∅A or x∈∅B}
Intersection- We denote the intersection of two sets as- A∩B, which is the set of all elements which belong to A and B.
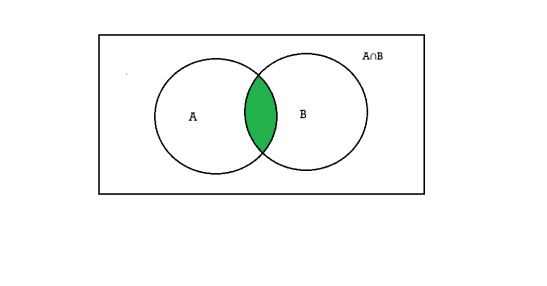
That is-
A∩B = {x |x∈∅A and x∈∅B }
Note- Two sets are said to be disjoint if they have no common elements in common.
Example: If A = {1, 2, 3, 4, 5, 6}, B = {4, 5, 6, 7, 8, 9} and C = {5, 6, 7, 8, 9, 10}
Then-
A∪B = {1, 2, 3, 4, 5, 6,7, 8, 9}
A∪C = {1, 2, 3, 4, 5, 6,7, 8, 9,10}
B∪C = {4, 5, 6,7, 8, 9, 10}
A∩B = {4, 5, 6}
A∩C = {5, 6}
B∩C = {5, 6, 7, 8, 9}
Property-1-
An element x belongs to the union A∪B if x belongs to A or x belongs to B; hence every element in
A belongs to A ∪B, and every element in B belongs to A ∪B. That is,
A ⊆A ∪B and B ⊆A ∪B
Property-2-
An element x belongs to the union A∪B if x belongs to A or x belongs to B; hence every element
A belongs to A ∪B, and every element in B belongs to A ∪B. That is,
A ⊆A ∪B and B ⊆A ∪B
Complements, differences, and symmetric differences-
Complement-
The complement of a set A, denoted by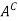
, is the set of elements that belong to U(universal set)but which do not belong to A. That is
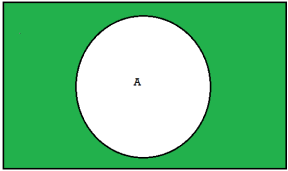
= {x | x ∈U, x /∈A}
Difference-
The difference between A and B, denoted byA\B or A-B, is the set of elements that belong to A but which do not belong to B that is-
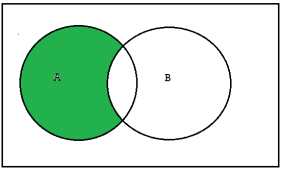
A-B = {x | x ∈A, x / ∈B}
The set A\Bor A-Bis read “A minus B”.
Symmetric difference-
The symmetric difference of sets A and B, denoted by A⊕B, consists of those elements which belong to A or B but not to both. That is
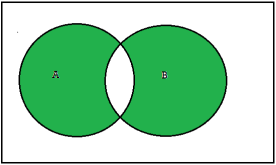
A ⊕B = (A ∪B)-(A ∩B) or A ⊕B = (A-B) ∪(B-A)
The cardinality of sets-
If A is a finite set with n distinct elements, then n is called the cardinality of A. The cardinality of A is denoted by |A| [or by n (A)].
Example: Let A = {a, b, c, d}, then A is a finite set and |A| = 4
The cardinality of the union of two sets-
Number of elements in A ∪B: (Cardinality of the union) If A and B are any two finite sets then, the numbers of elements in A ∪B, denoted by | A ∪B | is given by | A ∪B | = | A | + | B | −| A ∩B |
The principle of inclusion and Exclusion-
Let we have A andB are finite sets. Then A ∪B and A ∩B are
Finite and
n(A ∪B) = n(A) + n(B) −n(A ∩B)
That is, we find the number of elements in A or B (or both) by first adding n(A) and n(B) (inclusion) and then
Subtracting n(A ∩B) (exclusion) since its elements were counted twice
For three sets-
n(A ∪B ∪C) = n(A) + n(B) + n(C) −n(A ∩B) −n(A ∩C) −n(B ∩C) + n(A ∩B ∩C)
Finite set-
If a set has a finite number of elements then the set is said to be a finite set.
Examples:
1. {2, 5, 9, 8, 11, 15, 19, 85}
2. The set of all vowels in English alphabets
3. The set of students in of high school in a particular school.
Infinite set-
If a set has an infinite number of elements then the set is said to be an infinite set.
Examples:
1. The set of all-natural numbers.
2. The set of total points on a line.
Countable and uncountable sets-
A set S is said to be countable if it is either a finite set or a countably infinite set.
A set is said to be uncountable otherwise.
Example-
Suppose we have a set of even natural numbers N = {2n: n∈N }. We can find a Bijection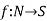
with the formula 
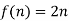. So we can say that the set is Countably infinite and also countable.
The set of odd natural numbers is also countably infinite.
Countably infinite and uncountably infinite sets-
Any set which can be put in a one-to-one correspondence with integers so that the prescription can be given for identifying its members one at a time is called a countably infinite set.
Any set which can not be put in a one-to-one correspondence with integers is said to be an uncountably infinite set.
Multi-set-
A multi-set is a generalization of a set where the repetition of elements matters.
Like {4, 5, 6} and {5, 4, 6} are the same multi-set but the set {5, 5, 4, 6} is the different multi-set as there is repetition of the elements.
So that, “A multi-set is a set-like, unordered collection where multiplicity(repetition) of the elements matters.
Here multiplicity means how many times an element occurs in the set.
Notation-
If an element ‘a’ occurs ‘n’ times in a multi-set A then it can be represented as -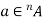 
.
For example-
, 
, 
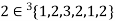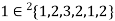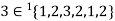
Relations and their properties-
We define a relation in terms of ordered pairs-
An ordered pair of elements of x and y, where x is the first element and y is the second element, is denoted by (x, y),
(x, y) = (p, q)
If and only if x = p and y = q
Thus (x, y)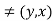
unless x = y
Product sets-
Suppose we have two sets X and Y. The set of all ordered pairs (x, y) where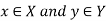 
is called the Cartesian product of X and Y.
It is represented as follows-
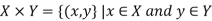
And it is read as X cross Y.
Relation-
Let X and Y are two sets, A relation from X to Y is a subset of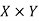 
.
Now suppose R is a relation from X to Y, then R is a set of ordered pairs where each first element comes from Xabd each second element comes from Y.
For each pair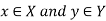 
, one of the following rules is true-
1. 
2.
The domain of a relation R is the set of all first elements of the ordered pairs which belong to R, and range is the second element.
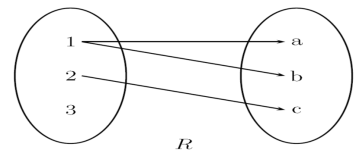
Pictorial representation of relations-
Let A = {1, 2, 3}, B = {a, b, c} and R ={(1, a), (1, b), (2, c)}
Then this relation can be represented as in picture format-
Inverse relation-
Let R be any relation from set X to set Y. The inverse of R is the relation from Y to X which consists of those ordered pairs which, when reversed, belong to R, such that-
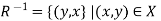
Example- If R = {(1, x),(1, y),(2, z)} then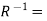 
{(x, 1),(y, 1),(z, 2)}
Composition of relations-
Let X, Y and Z are three sets and R be a relation from X to Y and S is a relation from Y to Z.
So that R is a subset of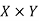 
and S is a subset of 
.
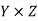Then R and S give a relation from X to Z which is denoted by RoS,
And can be defined as follows-
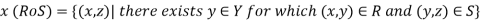
The relation RoS is called the composition of R and S.
Note- If R is a relation on a set A, that is, R is a relation from a set A to itself. Then the composition of R is RoR. Denoted by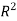 
.
Types of relations-
1. Reflexive relations
A relation R on a set X is reflexive if xRx for every x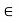
X. That is is (x, x)
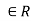for every x
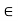X. Thus R is not reflexive if there exists x
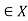such that (x, x) does not belong to R.
2. Symmetric and anti-symmetric relations-
A relation R on a set X is said to be symmetric if whenever xRy then yRx, that is if whenever (x, y)∈R then (y, x)∈R
R is said to be anti-symmetric if (x, y)∈X such that (x, y)∈R but (y, x)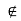
R
Transitive relation-
A relation R on a set X is said to be transitive if whenever xRy and yRzthen xRz, that is, if whenever (x, y), (y, z)∈R then (x, z)∈R
Equivalence relation-
A relation is a set R is said to be an equivalence relation in A, If R is reflexive, symmetric, and transitive.
Irreflexive relation
A relation R on a set A is irreflexive if aRafor every a ∈A
Example-
Let A = {1, 2, 3} and
R = {(1, 2), (2, 3), (3, 1), (2, 1)}
Then the relation R is irreflexive on A.
Asymmetric relation-
A relation R defined on a set A is asymmetric if whenever aRb, then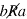 
.
Example:
Let A = {a, b, c} and R = {(a, b), (b, c)} be a relation on A. Then R is a symmetric.
Compatible relation-
A relation R in A is said to be a compatible relation if it is reflexive and symmetric.
If R is an equivalence relation on A, then R is compatible relation on A.
Universal relation-
A relation R in a set A is said to be universal relation if
R = A × A
Example:
Let A = {1, 2, 3}, then
R = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}
Is a universal relation on A.
Complementary relation-
Let R be a relation from A to B, then the complement of R denoted by R′and is
Expressed in terms of R as follows;
ARbif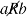 
Example-1: A = {2, 3}, B = {3, 4, 5, 6} and R is a relation from A to B defined as follows-
(a, b) ∈R if “a divides b” write the solution set of R.
Sol: 2 divides 4 and 2 divides 6
⇒(2, 4) ∈R and (2, 6) ∈R
3 divides 3, 3 divides 6
⇒(3, 3) ∈R and (3, 6) ∈R
4 divides 4 ⇒(4, 4) ∈R
Thus R = {(2, 4), (2, 6), (3, 3), (3, 6), (4, 4)}
Example-2: Let Z denote the set of integers and the relation R in Z be defined by “aRb” if a – b is an even integer”. Then show that R is an equivalence relation.
Sol.
1. R is reflexive; since
∅ = a −a is even, hence a R a for every a ∈ Z.
2. R is symmetric:
If a – b is even then b – a = – (a – b) is also even hence a R b ⇒b R a
3. R is transitive: for if a R b and b R c then both a – b and b – c are even.
Consequently, a – c = (a – b) + (b – c) is also even.
∴a R b and b R c ⇒ a R c
Thus, R is an equivalence relation.
n-ary relations and their applications-
An n-ary relation is a set of ordered n-tuples.
For any set S, a subset of the product set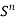 
is called an n-ary relation on S.
Or it can be defined as-
Let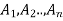 
be the sets. An n-ary relation on these sets is a subset of 
.
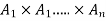The sets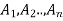 
are called the domains of the relation and n is called its degree.
Note-
1. The domain of an n-ary relation is called a primary key when the value of the n-tuple from this domain determines the n-tuple.
2. The current collection of n-tuple in a relation is called the extension of the relation.
3. When the values of a set of domains determine an n-tuple is a relation
Then the Cartesian product of these domains is called a composite key.
Matrix representation of relations-
Let there are two sets A and B and R is a relation from A to B, then R can be represented as a matrix called the relation matrix of R.
We denote this as-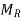 
If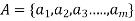 
and 
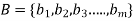are two finite sets that contain m and n elements. R is a relation from A to B.
Then the relation matrix of R is the m by n matrix-
Defined as-
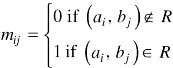
Example-1: If A = {1, 2, 3} and R = {(x, y): x<y}, then represent it as matrix.
Sol.
Here we have- R = {(1, 2), (1, 3), (2, 3)}
Then
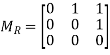
Example-2: Let A = {1, 4, 5} and R = {(1, 4), (1, 5), (4, 1), (4, 4), (5, 5)}, find relation matrix of this relation.
Sol. We have-
R = {(1, 4), (1, 5), (4, 1), (4, 4), (5, 5)},
Then,
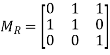
Pictorial representation of relations (Digraph)-
Suppose R is the relation on the set A =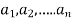 
then the elements 
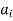of A are represented by nodes.
If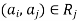 
we connect the vertices 
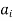and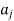 
and put an arrow in the direction from 
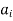to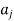 
.
If (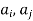
) ∈R and (
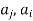)∈R then we draw two arcs between 
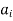and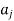 
(sometimes by one arc which starts from node 
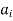and relatives to node 
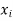(such an arc is called a loop).
When all the nodes corresponding to the ordered pairs in R are connected by arcs with proper arrows, we get a graph of the relation R.
If Ris reflexive, then there must be a loop at each node in the graph of R. If R is symmetric, then (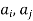
)∈R implies (
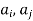) ∈R and the nodes
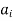and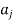 
will be connected by two arcs (edges) one from 
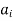to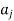
and the other from 
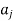to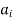 
Example-: If A = {1, 2, 3, 4} and R = {(1, 1), (1, 2), (2, 1), (2, 2), (2, 3), (2, 4), (3, 4), (4, 1), (4, 4)} Construct the digraph of R.
Sol.
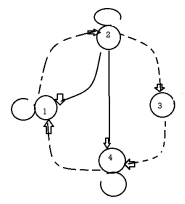
Example- Find the relation from the following digraph-
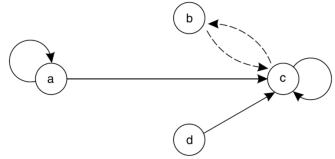
Sol. The relation R of the digraph is
R = {(a, a), (a, c), (b, c), (c, b), (c, c), (d, c)}
Closure properties-
Suppose we have a set X and the collection of all relations on X. Let P be a property of such relations.
A relation with property P will be called a P-relation.
Note that the P-closure of a relation R on X is written as- P(R), is a P-relation such that-
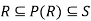
For every P-relation S containing R.
Functions-
Let X and Y are two sets. A relation f from X to Y is said to be a function if for every x ∈ X there is a unique element y ∈ Y, such that (x, y) ∈ X
We denote it as f: X → Y, which means f is a function from X to Y.
We represent the function as-
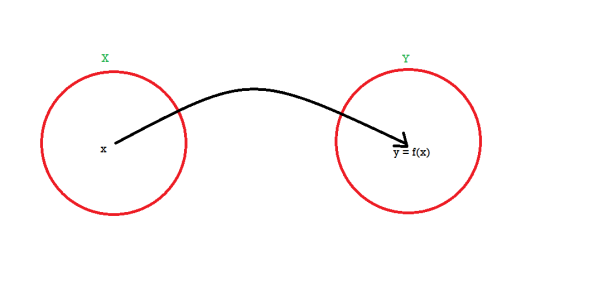
Example: Let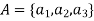 
and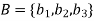 
And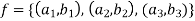 
Hence the function can be represented as-
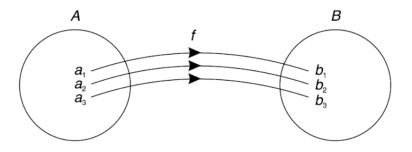
Here A is called the domain of f and B is called the co-domain of f
Surjective function (Onto-Mapping)-
A mapping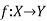 
is said to be onto-mapping if the range set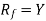 
If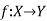 
is onto then each element of B if f-image of at least one element of X.
That means.
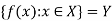
A mapping is said to be into if it is not onto.
Injective function (One-To-One Mapping)-
A mapping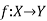 
is said to be one-to-one mapping if distinct elements of X are mapped into distinct elements of Y.
That means if f is a one-to-one mapping, then-
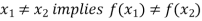
Or
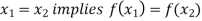
Bijective functions (One-To-One, Onto)-
A mapping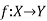 
is said to be bijective mapping if it is both one-to-one and onto.
Identity function (Identity Mapping)-
If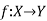 
is a function such that every element of X is mapped onto itself then f is said to be an identity mapping.
We denote identity mapping by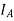 
.
If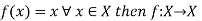 
is an identity mapping.
Partial functions-
Let X and Y set and A be a subset of X. A function f from A to Y is called a partial function from X to Y. The set A is called the domain of f.
Invertible function-
A function f from a set X to a set Y is said to be an invertible function if there exists a function g from Y to X, such that-
f(g(y)) = y
And
g(f(x)) = x
For every x ∈ X and y∈ Y
Constant function-
Let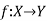 
then f is said to be a constant function if every element of X is mapped onto the same element of Y.
Inverse functions-
Let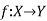 
is a one-one and onto mapping, then 
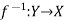is called the inverse mapping of f.
Inverse mapping can be defined as-
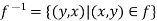
Composition of functions-
Let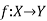 
and
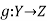are two mappings, then the composition of these two mappings f and g are denoted by gof is the mapping from X into Z.
It is defined as-
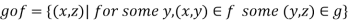
That means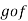 
is a mapping defined as below-
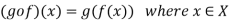
Example-1: Show that the inverse of an invertible mapping is unique.
Sol
Let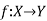 
By any invertible mapping,
Let,
g: Y→X
h: Y→X
Are two different inverse mappings of f.
Let y ∈ Y and
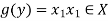
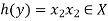
Now-
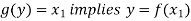
And
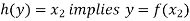
So that-
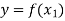and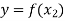
Now-
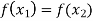
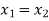
Which shows that g(y) = h(y)∀ y ∈ Y
So that the inverse of f is unique.
Example-2: Prove that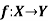 
is both one-one and onto then 
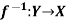is both one-one and onto.
Sol.
Let f: X→Ybe both one-one and onto.
Then there exist elements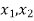 
∈X, and elements
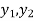∈Y
Such that
f(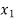
) = 
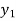, and f (
) =
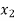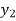
Or
= 
(
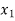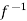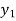) and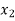 
= 
(
)
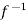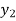Now,
Let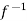 
(
) =
(
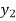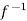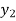), then
(
) =
(
)
⇒
= 
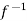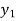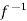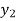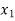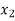
⇒f(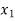
) = f (
)
⇒
= 
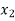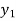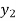
Thus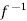 
is one-one
Since f is onto, for y∈Y, there is some element x∈X, such that f (x) = y.
Now
f(x) = y
⇒x=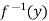 
So that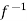 
is onto.
Hence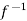 
is both one-one and onto.
Mathematical induction is a mathematical technique that is used to prove a statement, a theorem or a formula is true for every natural number.
The technique has two steps to prove any statement-
1. Base step (it proves that a statement is true for the initial value)
2. Inductive step (it proves that is the statement is true for nth iteration then it is also true for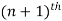 
iteration.
Example-1: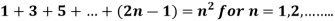 
Sol. Here for n = 1, 1 = 1²
Now let us assume that the statement is true for n = k
Hence we assume that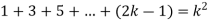 
is true.
Now we need to prove that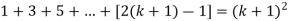
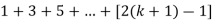
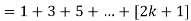
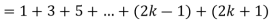
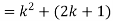
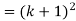
So that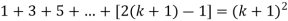 
which satisfies the second step.
Hence-
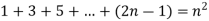
Example-2: Prove 1+2+...+n = n(n+1)/2 using a proof by induction
Sol.
Let n=1: 1 = 1(1+1)/2 = 1(2)/2 = 1 is true,
Step-1: Assume n=k holds: 1+2+...+k = k(k+1)/2
Show n=k+1 holds: 1+2+...+k+(k+1)=(k+1)((k+1)+1)/2
Substitute k with k+1 in the formula to get these lines. Notice that I write out what I want to prove.
Step-2: Now start with the left side of the equation
1+2+...+(k+1)=1+2+...+k+(k+1)
=k(k+1)/2 + (k+1)
=(k(k+1)+2(k+1))/2 by 2/2=1 and distridution of division over addition
=(k+2)(k+1)/2 by distribution of multiplication over addition
=(k+1)(k+2)/2 by commutativity of multiplication
Example-3: Prove the following by using the principle of mathematical induction for all n ∈ N-
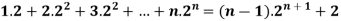
Sol. Here, n = 1,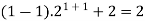 
, which is true
Step-1: Assume n = k holds-
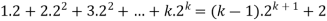
Now show n = k + 1 also holds-
Consider-
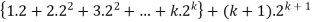
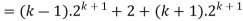
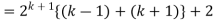
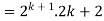
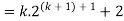
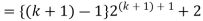
Which is also true for n = k + 1.
Hence proved.
Strong inductions-
It is another form of mathematical induction. By using this we can prove that a propositional function, P(n) is true for all positive integers n.
Working steps-
1. Base step- this proves that the initial proposition P(1) is true.
2. It proves that the conditional statement[P(1)∧P(2)∧P(3)∧⋯∧P(k)]→P(k+1) is true for positive integers k.
Discrete numeric functions-
The function whose range is the set of real numbers and whose domain is the set of real numbers is called the numeric function.
For example-
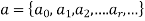
Is a numeric function.
Here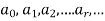 
represents the values of a at 0, 1, 2, 3......r...
Note- the sum and product of two numeric functions are also numeric functions.
The forward difference- if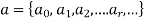 
Is a numeric function then
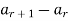
Is called the forward difference at r.
This is denoted by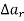 
The backward difference- if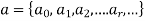 
Is a numeric function then
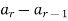
Is called the backward difference at r.
This is denoted by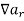 
Generating function-
Generating function is an alternative way to represent the numeric function.
For the numeric function-
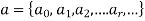
Let define an infinite series-
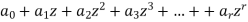
Which is called the generating function of a.
The generating function is denoted by A(Z).
The product of two generating functions can be defined as-
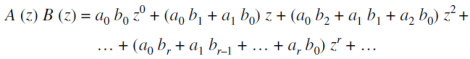
Recurrence relations-
The recursive formula to define a numeric function is called a recurrence relation.
A recurrence relation is also called a difference equation.
Linear recurrence relation-
Let r and k be two non-negative integers.
A recurrence relation of the form-
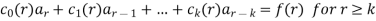
If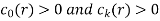 
then it is called a linear recurrence relation of degree k.
If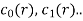 
are constant then it is called linear recurrence relation with constant coefficients.
If f(r) = 0 then it is called linear homogeneous relation.
The solution of recurrence relations-
Here we will discuss the substitution method of solving recurrence relation.
In this method the recurrence relation of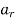 
is used again and again to solve the recurrence for general expression for 
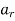in terms of r.
Note- A recurrence relation may or may not have a solution
Example: Solve the recurrence relation-
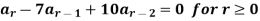
Sol.
Here we will multiply each term of the recurrence relation by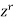 
, we get-
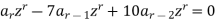
Taking the sum 2 to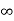 
, we get-
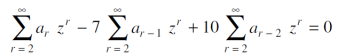
Now replacing each infinite sum by the corresponding equivalent expression given above, we get
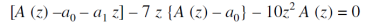
We get on simplifying-
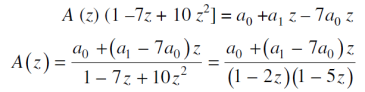
Decomposing A(z) as a sum of partial fractions, we can write-
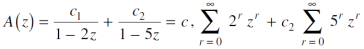
The solution is-
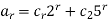
Example: Solve-
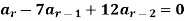
Sol. The characteristic equation will be
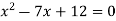
We get on middle term split-
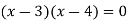
We get-
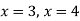
The solution is-
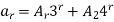
Pigeonhole principle (statement)-
If n pigeonholes are occupied by n + 1 or more pigeons, then at least one pigeonhole is occupied by more than one pigeon.
Example-1: Suppose a class contains 13 students, then two of the students (pigeons) were born in the same months (pigeonholes)
Example-2: Show that if seven numbers from 1 to 12 are chosen, then two of them will add up to 13.
Sol.
First, we will construct six different sets, each containing two numbers that add up to 13 as follows-
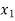= {1, 12}, 
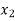= {2, 11}, 
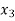= {3, 10}, 
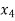= {4, 9}, 
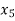= {5, 8}, 
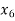= {6, 7}.
Each of the seven numbers belongs to one of these six sets.
Since there are six sets, then according to the pigeonhole principle that two of the numbers chosen belong to the same set. These numbers add up to 13.
Generalized pigeonhole principle-
If n pigeonholes are occupied by kn+ 1 or more pigeons, where k is a positive integer, then at least one pigeonhole is occupied by k + 1 or more pigeons.
Example- Find the minimum number of persons in a group that three of them are born in the same month.
Sol.
Here the n = 12 months are the pigeonholes, and k + 1 = 3 so k = 2. Hence among
Anykn+ 1 = 25 students (pigeons), three of them are born in the same month.
Reference Books
1. B.S. Grewal: Higher Engineering Mathematics; Khanna Publishers, New Delhi.
2. B.V. Ramana: Higher Engineering Mathematics; Tata McGraw- Hill Publishing Company Limited, New Delhi.
3. Peter V.O’ Neil. Advanced Engineering Mathematics, Thomas ( Cengage) Learning.
4. Kenneth H. Rosem: Discrete Mathematics its Application, with Combinatorics and Graph Theory; Tata McGraw- Hill Publishing Company Limited, New Delhi
5. K.D. Joshi: Foundation of Discrete Mathematics; New Age International (P) Limited,
Publisher, New Delhi.
