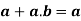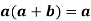Module-5
Lattices and Boolean Algebra
Partial orderings-
A relation R on a set Sis called a partial order relation in Sif R is, Reflexive Anti-symmetric, and transitive.
A set S together with a partial ordering R is called a partially ordered set.
We denote a partial order relation by the symbol ≤.
Comparability-
Suppose R be a partial order on Sand a, b ∈S whenever aRb or bRa, we say that a And b are comparable otherwise a And b are non-comparable.
Dual order-
If ≤is a partial order on a set S, then the converse of R is also a partial order on S. That means if ≤is a partial ordering on S, then ≥is also a partial ordering on S. (S, ≥) is called the dual of (S, ≤).
Partitions-
Let S be a non-empty set. Then the collection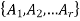 
of a subset of S is said to be a partition of S iff-
1. 
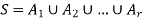
2. For any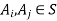 
Either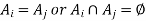 
Cross partition-
If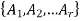 
and 
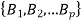both are a partition of set S which is non-empty, then 
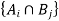forms a partition of S
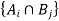is called a cross partition of S.
Ordered partition-
A partition a non-empty set is called an ordered partition of S if there is a specified order on the subsets of S.
An ordered t-tuple of sets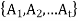 
is called a t-part ordered partition if the sets 
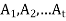form a partition of S.
Theorem-
The number ‘m’ of ordered partitions of a set S with ‘n’ elements into r cells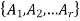 
, where for each ‘i’, n(
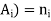– follows-
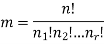
Example:
Find the number of ways to partition 10 peoples into four groups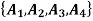 
So that two teams contain 3 persons and two teams containing 2 persons.
Sol.
By using the above theorem, we get-
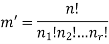
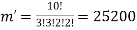ordered partitions
Here the group forms an unordered partition so that we divide m’ by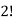 
Because of the two cells with three elements each and 
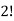Because of the two cells with two elements each.
So that-
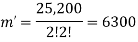
Example: There are 12 employees in a company. Find the number of ways that the 12 employees do three different tasks if four employees are to take each task.
Sol.
Here we find the number of ordered partitions of twelve employees into cells containing 4 employees each.
There are total -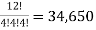 
partitions
Hence the required number of ways, the employees can do the task is 34,650.
Lattice as a partially ordered set
Lattices-
A lattice is a partially ordered set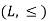 
in which every pair of elements a,b
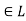has a greatest lower bound and a least upper bound
For example-
Suppose S be a non-empty set and L = P(S);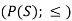 
that means (
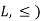is partially ordered.
If X and Y are two elements of L, then-
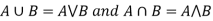
Hence (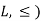
is a Lattice.
Axiomatic definition of Lattice-
Let L be a non-empty set closed under two binary operations denoted by ∧ and ∨.
Then L is said to be a Lattice if it follows the axioms given below, here a, b, and c are the elements of L.
1. Commutative law-
(i) a∧ b = b ∧ a (ii) a ∨ b = b ∨ a
2. Associative law-
(i) (a ∧ b) ∧ c = a ∧ ( b ∧ c) (ii) (a ∨ b) ∨ c = a ∨ (b ∨ c)
3. Absorption law-
(i) a∧ (a∨b) = a (ii) a∨(a∧b) = a
To show which operation is involved we denote the Lattice by (L, ∧, ∨)
Theorem-Let (L, ≤) be a lattice in which ‘⋅’ And ‘+’ denote the operations of meet and join respectively.
Then
a≤b ⇔a ⋅b = a ⇔a + b = b ∀a, b, c ∈L
Proof: Suppose a ≤b
As we know that a ≤a so that a ≤a. b but according to definition a.b≤a
So that- a ≤b ⇒a ⋅b = a
Let a ⋅b = a
But this is possible only if a ≤b which means a ⋅b = a ⇒a ≤b
∴a≤b⇒a ⋅b = a and a ⋅b = a ⇒a ≤b
Combine these two, we get
a≤b ⇔a ⋅b = a
Now let,
a⋅b = a,
Then we have
b + (a ⋅b) = b + a + a + b
But,
b + (a ⋅b) = b
Hence a + b = b
Similarly by assuming a + b = b
We can show that a ⋅b = a
Hence a ≤b ⇔a ⋅b = a ⇔a + b = b = a
Isomorphic Lattice-
Two lattices L and L’are said to be isomorphic if there is a one-to-one correspondence
f: L →L’
Such that
f (a ∧b) = f (a) ∧f (b) and f (a ∨b) = f (a) ∨f (b)
For any elements a, b in L.
Note-
1. A lattice is called complete if each of its non-empty subsets has a least upper bound and a greatest lower bound.
2. A lattice L is complemented if it is bounded and if every element in L has a complement.
3. Let ( L, ⋅, +, 0, 1) be a bounded lattice and a ∈L. If there exists an element b ∈L
Such that
a⋅b = 0 and a + b = 1
Then b is called the complement of a.
Sub Lattices and Direct products-
Sub Lattices-
Let (L, ≤) be a lattice. A non-empty subset A of L is called a sublattice of L if
a + b ∈A and a ⋅b ∈A whenever a ∈A and b ∈A.
If A is a sublattice of L, then A is closed under the operations of ‘’ ⋅and ‘+’.
Direct product-
Let (L1, *, +) and (L2,∧, ∨) be two lattices. The algebraic system (L1 × L2,...,+)
In which the binary operation + and ‘’ ⋅are on L1 × L2 defined as
(a1, b1) ⋅(a2 ,b2 ) = (a1 ∗a2 , b1 ∧b2 )
(a1, b1 )+ (a2 ,b2 ) = (a1 ⊕a2 , b1 ∨b2 )
For all (a1, b1) and (a2, b2) (a2 ,b2 ) ∈L1 × L2
Is called the direct product of the lattices L1 and L2.
Note-
1. Let (L, ⋅, +, 0, 1) be a lattice L is said to complemented lattice if every element has at least one complement.
2. A lattice (L, ⋅, +) is called a distributive lattice if for any a, b, c ∈L
a⋅ (b + c) = (a ⋅b) + (a ⋅c) and
a + (b ⋅c) = (a + b) ⋅ (a + c)
3. Let (L, ≤) be a lattice, with an upper bound 1. An element a ∈L is said to be meet irreducible if a = x ⋅y implies a = x or a = y.
If a ≠0 then a is meet irreducible if and only if a has a unique immediate successor
Hasse Diagram-
The elements in the Hasse diagram are represented as vertices and it is a pictorial representation of finite order on a set.
Two related vertices of a partial order are connected by a line if they are related.
Example-1: If A = {1, 2, 3} and ≤ be a relation on A. The Hasse diagram will be-
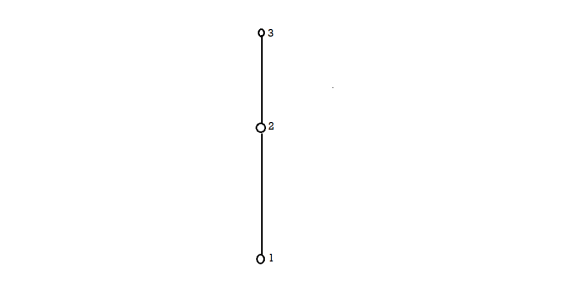
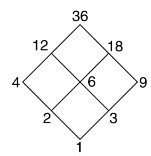
Example-2: Draw the Hasse diagram of the positive division of 36.
Sol.
We have
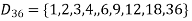
Suppose R is the partial order relation on 
The Hasse diagram will be-
Example-3: Let B = {a, b, c, d, e} then the Hasse diagram defines a partial order on B in a natural way. That is, d ≤ b, d ≤ a, e ≤ c, and so on.
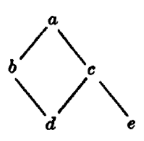
Definition- minimal element-
Suppose (A,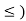 
denote the partially ordered set. Then an element 
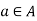is said to be a minimal member of a relative to 
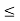if for no 
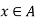, is x < a.
Definition- maximal element-
An element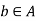 
is said to be a maximal element of A relative to the partial ordering 
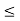if for no 
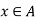, is b < a.
Upper bounds and lower bounds-
Suppose (A,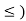 
denote the partially ordered set and let B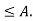 
Any element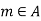 
is called the upper bound for B if 
.
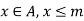Similarly, an element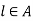 
is called lower bound for B if for all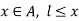 
Example: A = {1, 2, 3…,6} be ordered as shown in the picture below-
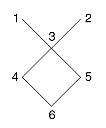
And if B = {4, 5} then the upper bounds of B are 1,2,3 and the lower bounds of B is 6.
Let there are two partially ordered set P(X,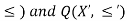 
, these two POSETs will be called isomorphic ordered set if there is bijection f from X to 
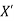such that 
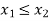precisely when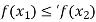 
Note –
Suppose three sets A, B and C are partially ordered then-
- A is isomorphic to itself.
- If A is isomorphic to B, then B is isomorphic to A
- If A is isomorphic to B and B is isomorphic to C then A is isomorphic to C.
Example: Let A = P ({0,1}) ordered by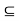 
. Let B = {1, 2, 3, 6} with n
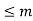iff n|m then A and B are isomorphic.
Lattices-
A lattice is a partially ordered set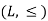 
in which every pair of elements a,b
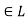has a greatest lower bound and a least upper bound
For example-
Suppose S be a non-empty set and L = P(S);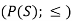 
that means (
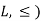is partially ordered.
If X and Y are two elements of L, then-
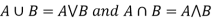
Hence (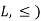
is a Lattice.
Bounded lattice-
If L is a lattice, then every pair of elements of L has a least upper bound and a greatest lower bound. If A is a finite subset of A, then A has both the least upper bound and greatest lower bound. This property may not hold if A is not a finite subset of L, we find the greatest lower bound and least upper bound of a subset of a lattice as follows.
Let (L, ⋅, +) be a lattice and A ≤L be a finite subset of L. The greatest and least upper bound of Aare defined as
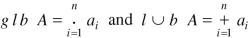
Where A = {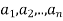
}.
Note-
1. A lattice is called complete if each of its non-empty subsets has a least upper bound and a greatest lower bound.
2. Let ( L, ⋅, +, 0, 1) be a bounded lattice and a ∈L. If there exists an element b ∈L
Such that
a⋅b = 0 and a + b = 1
Then b is called the complement of a
3. Let A be a non-empty set and L = P (A). Then every element of L has a complement.
Sub lattice
Let (L, ≤) be a lattice. A non-empty subset A of L is called a sublattice of L if
a + b ∈A and a ⋅b ∈A whenever a ∈A and b ∈A.
If A is a sublattice of L, then A is closed under the operations of ‘’ ⋅and ‘+’.
Example: Let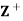 
be the set of all positive integers and let D denote the relation “division” in 
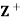such that for any a, b ∈
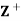, a D b if a divides 6. Then (
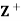, D) is a lattice in which a + b = LCM of a and b and a ⋅b = GCD of a and b.
The direct product of the lattices-
Let (L1, *, +) and 2 (L,∧, ∨) be two lattices. The algebraic system (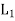
× 
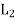, ..., +) in which the binary operation + and ‘.’are on 
× 
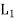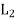defined as
(a1, b1) ⋅(a2 ,b2 ) = (a1 ∗a2 , b1 ∧b2 )
(a1, b1 )+ (a2 ,b2 ) = (a1 ⊕a2 , b1 ∨b2 ) for all (a1, b1) and (a2, b2) (a2 , b2 ) ∈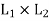
is called the direct product of the lattices 
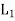and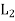 
Distributive lattice-
A lattice (L, ⋅, +) is called a distributive lattice if for any a, b, c ∈L
a⋅ (b + c) = (a ⋅b) + (a ⋅c) and
a + (b ⋅c) = (a + b) ⋅ (a + c)
Note- The power set of a non-empty set A is a lattice under the operation ∩and ∪is a distributive lattice.
Definition-
Two statement formulas P and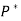 
are said to be duals of each other if either one can be obtained from the other by replacing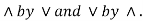 
Example: Show that-
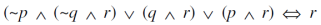
Sol.
Solution-
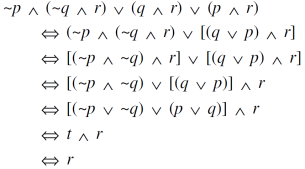
Note- ‘t’ denotes tautology
Example: Simplify-
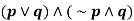
Sol. We have-
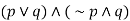
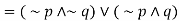
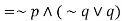
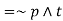
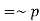
Definition-
A Boolean algebra is a distributed complemented lattice having at least two members as well as 0 and 1.
A Boolean algebra is denoted by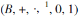 
.
Here (B, +, .) is a lattice which has two binary operations + and ., called the join and meet respectively is a unary operation in B.
The following axioms are satisfied-
- There exist at least two elements a, b in B, and that ‘a’ is not equals to ‘b’.
2. For every for all,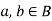 
(i)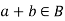 
(ii)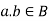 
3. For all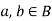 
[commutative laws]
(i)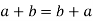 
(ii)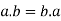 
4. For all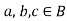
[associative law]
(i)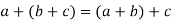 
(ii)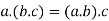 
5. For all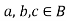
[distributive law]
(iii)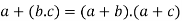 
(iv)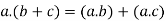 
6. There exists of B such that-
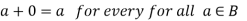
Element 0 is called the zero elements.
7. There exists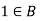 
sum that-
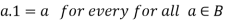
1 is called the unit element.
8. Existence of complement- for every for all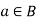 
there exists an element 
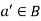such that-
(i) a + a’ = 1 and (ii) a.a’ = 0
Note- in Boolean algebra-
- 0’ = 1
- 1’ = 0
Theorem-1- 
Proof:
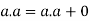
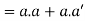
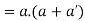
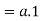
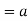
Theorem- for any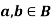 
Proof:
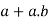
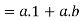
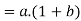
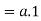
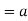
2. we have-
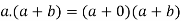
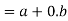
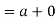
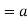
Algebra method-
Example: Simplify z (y+z) ((x + y + z).
Sol.
z(y + z) (x + y + z)
= (z y + z z) (x + y + z)
= (z y + z) (x + y + z)
= z (y + 1) (x + y + z)
= z (x + y + z)
= z x + z y + z z
= z x + z y + z
= z (x + y + 1)
= z (x + 1)
= z
Example: Simplify Y = (P + Q) (P + Q′) (P′+ Q)
Sol.
Y = (P + Q) (P + Q′) (P′+ Q)
= (P P+ P Q′+ P Q + Q Q′) (P′+ Q)
= (P + P Q′+ P Q + 0) (P′+ Q)
= (P + P Q′+ P Q) (P′+ Q)
= P P1 + P Q + P Q′P′+ P Q′Q + P Q P′+ P Q Q
= 0 + P Q + 0 + 0 + 0 + P Q
= P Q + P Q
= P Q
Example: Minimize the expression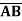 
+
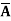+ A B
Sol.
+ 
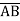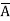+ A B
= 
+ 
+ 
+ A B
= 
+ 
+ 
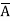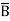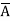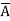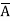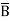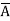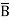+ A B
= 
+ 
+ A B
= 
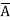+ A B +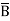 
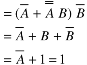
Hence
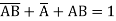
Prime Implicants-
Suppose E be a Boolean expression. A fundamental product P is called a prime implicant of Boolean expression E if P + E = E but no other fundamental product included in P has this property.
Logic gates are electronic circuits that can be used to implement the most elementary logical expression.
There are three basic logic gates-
- OR- gate
- AND-gate
- NOT-gate
Note- NAND-gate, the NOR-gate, the EX-OR gate, and the EX-NOR gate are derived from the three basic logic gates.
Now we will discuss them one by one-
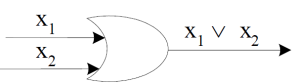
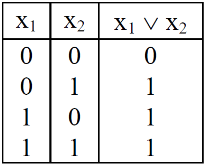
OR-gate-
This is a logic circuit with two or more than two inputs and outputs.
An OR-gate receive inputs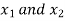 
and gives the output, denoted by 
.
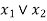We use the standard pictorial representation of OR-gate as-
AND-gate-
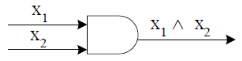
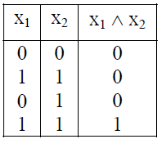
An AND-gate is a logic circuit having two or more than two inputs and one output.
The truth table and pictorial representation is given below-
NOT-gate-
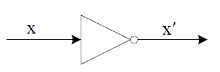
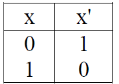
A NOT-gate is one input and one output logic gate. The output of a NOT-gate is always the complement of the input. A NOT-gate is also known as an inverter or a complementing circuit.
NOR- gate-
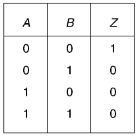
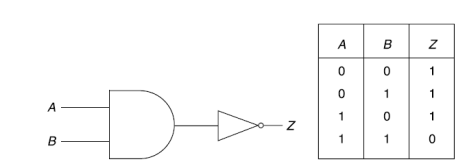
NAND- gate-
The NAND-gate has two or more input signals but only one output signal. The NAND-gate is a contraction of NOT AND. It can have many inputs as desired.
EX-OR gate-
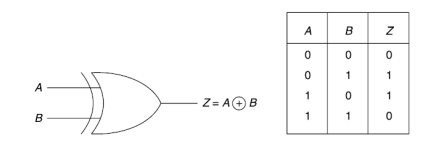
EX-NOR gate-
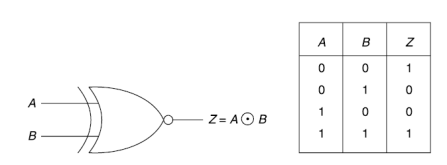
Example: construct the logic circuit represented by the Boolean expression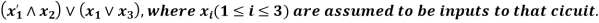 
Sol.
The logic circuit for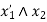 
is-
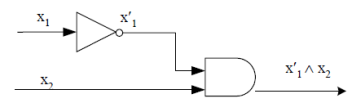
And the logic circuit for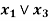 
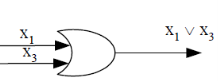
Circuitry for the expression-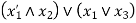
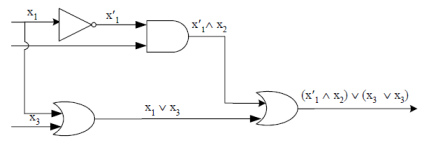
Example: Construct a NAND-gate for the expression-
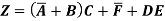
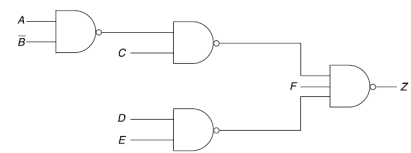
Truth table-
The truth table shows the true values of a statement.
Boolean function-
Suppose (B, +,. , ‘, 0, 1) be a Boolean algebra.
A function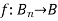 
which is associated with a Boolean expression in ‘n’ variables is called a Boolean function.
To transform Boolean expression E into a sums-of-products form- first, we use
De Morgan’s laws and involution law, to convert E into a form which contains only sum and products of literals then we use distributive law to transform E into a sums-of-products form. Again to transform each product in E into 0 or a fundamental product. This is done by using the commutative, idempotent, and complement laws. Finally, we use the absorption law to get the sums-of-product form of E.
To obtain a complete sum-of-product form of E. We involve all the variables in each product of the sum of- product form of E.
Example: Express-
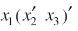
In an equivalent sum-of-products canonical form in three variables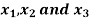 
Sol.
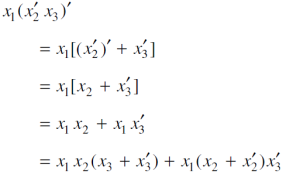
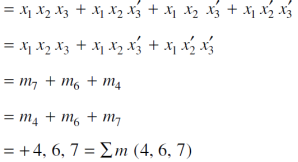
Karnaugh Maps-
The Karnaugh method is a systematic method for simplifying Boolean function.
It is a graphical representation of the truth table with a square representing each minterm.
If a function has ‘n’ variables then the Karnaugh map will have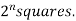 
One variable Karnaugh map is-
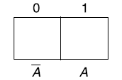
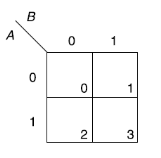
Two variable Kanaugh map representing minterm-
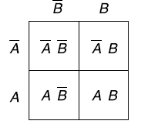
Or
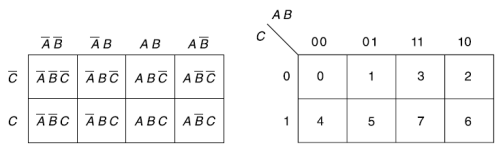
Karnaugh map for three variables-
Reference Books
1. B.S. Grewal: Higher Engineering Mathematics; Khanna Publishers, New Delhi.
2. B.V. Ramana: Higher Engineering Mathematics; Tata McGraw- Hill Publishing Company Limited, New Delhi.
3. Peter V.O’ Neil. Advanced Engineering Mathematics, Thomas ( Cengage) Learning.
4. Kenneth H. Rosem: Discrete Mathematics its Application, with Combinatorics and Graph Theory; Tata McGraw- Hill Publishing Company Limited, New Delhi
5. K.D. Joshi: Foundation of Discrete Mathematics; New Age International (P) Limited,
Publisher, New Delhi.
