Unit - 5
Arches
An arch is a curved beam in which horizontal movement at support is wholly or partially prevented. Hence there will be horizontal thrust induced at the support. The shape of an arch does not change with loading and therefore some bending may occur.
An arch is a vertical curved shape that spans a multiplied area and might or won't help the burden above it, or in case of a horizontal arch like an arch dam, the hydrostatic strain in opposition to it.
Arches can be synonymous with vaults; however, a vault can be outstanding as a non-stop arch forming a roof. Arches regarded as early because the 2d millennium BC in Mesopotamian brick architecture and their systematic use began out with the historic Romans, who had been the primary to use the approach to a huge variety of structures.
Arches may be classified based on material used, structural behavior and loaded area.
- Based on material used
- Steel arch
- Reinforced concrete arch
- Masonry arch
2. based on structural behavior
- Three hinge arch
- Two hinge arch
- Fixed arch
3. based on loaded area
- Open arch
- Closed arch
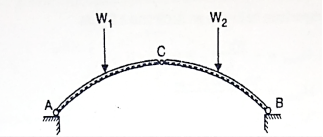
A three hinged arch is a statically determinate structure, having a hinge at each abutment or springing and also at the crown.
There are in all four reaction components (two at each hinge i.e. H and V). Three equations are available from the static equilibrium and one additional equation is available from the fact that the B.M. At the hinge at the crown is zero. Thus, the value of H can easily be calculated for any given load system.
A component of arch is shown in Fig.
A section of arch is subjected to three straining actions under the action of loads, these are
(1) Bending moment (M).
(ii) Normal thrust (N).
(iii) Radial shear (F).
The B.M. Is calculated using Eddy's theorem which is stated as, "The B.M. At any section of an arch is equal to the vertical intercept between the linear arch and the centre line of the actual arch."
B.M. At any section = Sum of moment due to loads Vertical reactions (R) and Horizontal Thrust (H).
= Beam moment + H. Moment
Diagram:
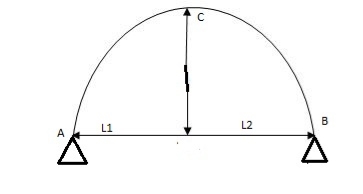
A three hinged arch consists of Two parts AC and BC hinged at C and supports A and B are two external hinges (Like an abutment).
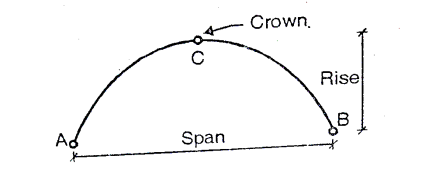
1. Span of an arch: The horizontal distance between Two lower hinge supports A and B is known as span of arch
2. Rise of the arch: When supports A and B are at the same levels, the height of crown (C) is called rise of the arch. If the shape of the arch is parabolic then it is called parabolic.
Diagram:
Equation type: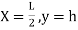 
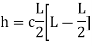
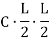
C=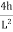
Equation of parabola is:
Y=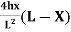
Steps of analysis of three hinged arch:
Step 1) Find reaction components
Draw F.B.D of arch taking two reaction components at each support and apply
Step 2) Find normal thrust and radial shear at any section.
Step 3) Find B.M. At any section
Use Mx= Beam moment - H moment
Parabolic Eqn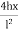
( lx)
Eddy's theorem states that the bending second at any segment of an arch is identical to the vertical intercept among the linear arch and the middle line of the real arch. For a 3 hinged parabolic arch, the diploma of static indeterminacy is zero.
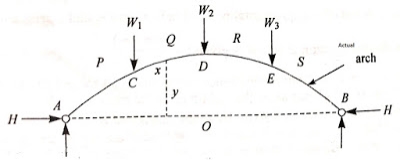
Actual Arch: The arch which follows both parabolic, round or elliptical form and are effortlessly built with aesthetic look is referred to as as real arch.
Consider an arch (2 or three hinged) as proven in determine subjected to the masses W1, W2 and W3. Let Va and Vb are the reactions at helps A and B. Let H is the horizontal response at every support.
Linear or theoretical arch: The arch which follows funicular polygon form after utility of collection of masses are known as as linear or theoretical arch.
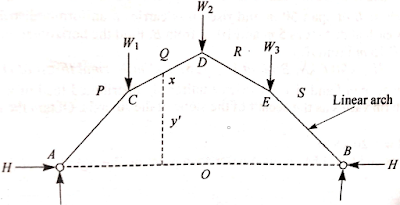
Consider the funicular polygon – ACDEB of arch as proven in determine in which the participants AC, CD, DE and EB are pin jointed and loaded with W1, W2 and W3 at factors C, D and E. Generally, the participants withinside the linear arch is subjected to compressive forces and joints ought to be in equilibrium.
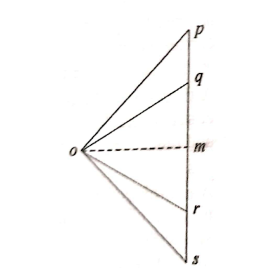
Referring to the vector diagram allow pq, qr and rs represents the hundreds W1, W2 and W3. Let OM represents Horizontal thrust, MP represents vertical response at A and MS represents vertical response at B of the arch. If the arch is supplied because the equal funicular shape (proven in fig 2) then the bending second for such sort of arch can be zero.
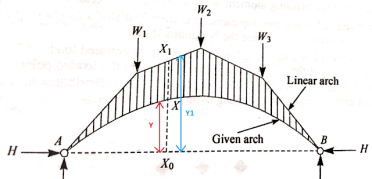
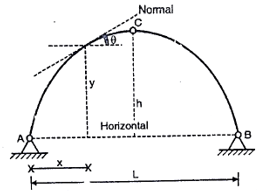
Figure indicates the aggregate of real arch and linear arch. Let x be the segment to decide the bending second, y and y1 be the rises for real and linear arch respectively. Bending second at segment X0-X = Hy Bending second at segment X0-X1 = Hy1 Net bending second on the overlapped part of X segment: H (y1 - y) Therefore, internet BM at segment X is proportional to the distinction in rise. i.e., (y1 - y)
Therefore Eddy’s Theorem states that "The bending second at any segment is proportional to the vertical intercept
1. Spandrel braced arch, moving load
Spandrel, additionally spelled spandril, the more or less triangular place above and on both aspect of an arch, bounded with the aid of using a line strolling horizontally thru the apex of the arch, a line growing vertically from the springing of the arch, and the curved extrados, or pinnacle of the arch.
For centuries, many homes used arches for entrances and as a manner to assist walls. In those structures, a spandrel is the kind of triangular area among arches and the wall or ceiling above them. Spandrels can be located among arches or among an arch and the square location round it.
2. Influence lines for three hinged parabolic arch
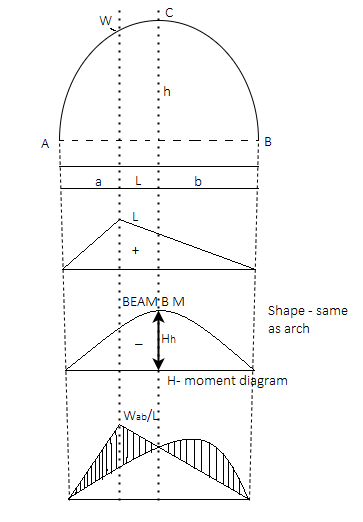
Bending moment diagram for three hinged arch:
We know that for an arch, bending moment at any point is equal to beam BM-Hy (Refer comparison between arch and beam). Hy is called H-Moment. It varies with respect to Y. Therefore the shape of BM due to Hy should be the shape of the arch. Therefore to draw the BMD for an arch, draw the BMD for the beam over that superimpose the H-moment
Diagram as shown in Fig.
2. Steps of analysis of three hinged arch:
Step 1) Find reaction components
Draw F.B.D of arch taking two reaction components at each support and apply
Step 2) Find normal thrust and radial shear at any section.
Step 3) Find B.M. At any section
Use Mx= Beam moment - H moment
Parabolic Eqn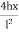
( lx)
Circular Eqn
IMP
At diffn level
= 
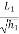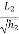
Parabolic Eqn for half portion
Y =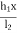 
(2l1 -x)
Y =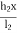 
(2l2 -x)
At same level Parabolic arch
Step1. Draw FBD
2. Find Real due to Equilibrium condition =0, efs = 0cm,
3. Consider half part of Arch (i.e. left/Right) find Horizontal thrust.
4. Find B.M. Consider parabolic can find vertical dossy
5. Find normal thrust I Radial shear.
At different level parabolic arch
Step 1) find length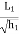 
= 
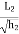, efy = 0
2. Consider half portion I take moment at c you will get VA& VB
3. Equating with Efy = 0 get H
4. Find normal thrust Radial Shear
Hinged parabolic Arch at some level
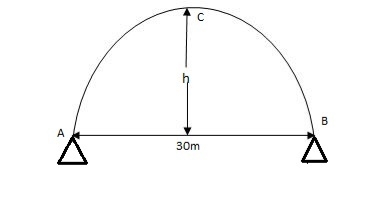
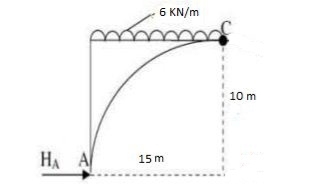
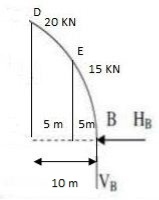
Example: A 3 hinged arch has a span of 30 cm & arise of 10m the arch carries of UDL 6 KN/M on the left half of the span it also carries two concentrated load of 16 KN I 20 KN at 5m I 10m from the right end determine an at support. B.M. At 10m from right I radial shear & normal trust at c from left end.
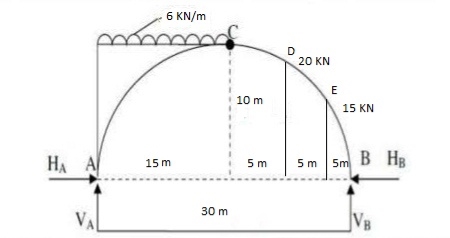
Step1. Draw FDB
Step2. Find resultant by equilibrium can
EMA = 0
6 x 15 x 7.5 – 20 x 20 – 16 x 25 + VB x 30 = 0
VB= 49.17kn
EFY = 0
VA + VB = 6 x 15 + 20 + 16
VA = 76.83 KN
EFx= 0
HA – HB = 0
HA = HB
Step3. Cut the arch from CPI
Consider left part of Arch AC
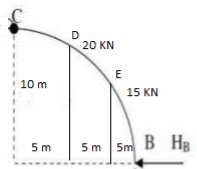
VA= 76.83 EMC = 0
EMC = 0 - 20 V 5 – 16 x 10 – H5 x 10
- 76. 83 x 15 + HA x 10 + 6 x 15 x 7.5 = 0
- HA = 47.75Kn HB = 47.75Kn
Consider any part you will get some on
RA=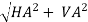
RB =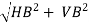 
Step 4 = Find BM at 10m from right end
20kn x = 10 m y =?
EMD yd = 4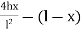
- 16x5 – HB x YDv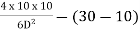
+ VB x 10olD =
- 16 X 5 -47.75 X 8.8+ 49.17 X 10 =
- MD = - 8.5KNM
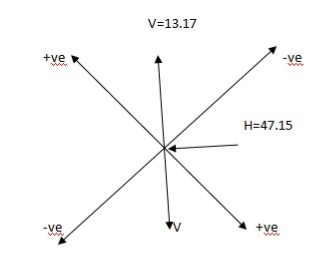
N = + HCOSO – Csinq
R = Hsinq + VcosQ
Q) Find by parabolic eq.n
l = 30, x = 15m
y =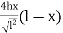 
y =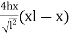 
Differentiate
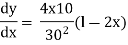
Tan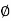
= 
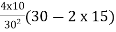
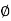= 0
N = 47.75 cos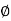
- 13.17 sino
N = 47.75 KN
R = 47.75 sino + 13.17 coso
R = 13.17kn
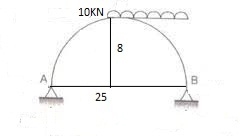
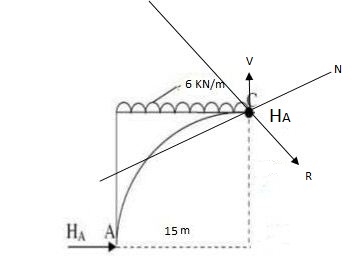
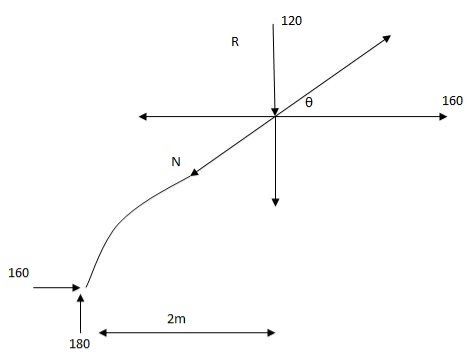
Example: A parabolic 3 hinged arch curries 4UDl 30kn/m on the left of the span it has a span of 16m. Iacenthaleire 3m. Determine the resultant ref 6 supports find the D. m. Normal trust I redial should udl xx 2m from left sun
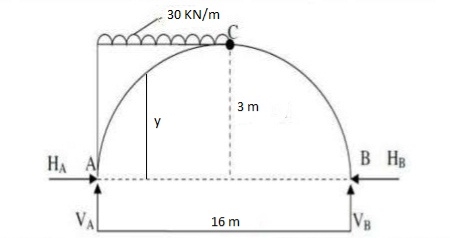
EmA= 0
VB X 16 – 30 X 8 X 4 = 0
VB = 60 KN
VA = 180 KN
EMc = 0
- VA X 8 + 4 X 3 + 30 X 8 X 4 = 0
H = 160 KN
HA = HB = 160 KN
RA =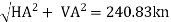 
RB=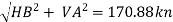 
B. m. At x = 2 m from A
By using parabolic Arch
Y =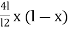 
X = 2m
L = eise – 3m
L = 16
Y =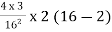 
Y = 1.3125
Mx =Yax 2 ++4 AXY + 30 x 2 x 1 =
- 18ax2 + 160 x 1.31 2 x 1
Mx = 90.4knm
Radial shear
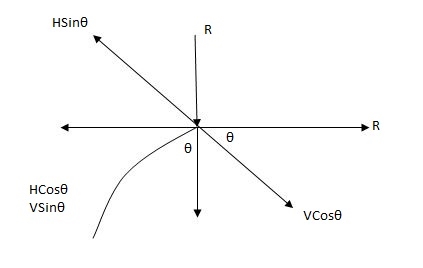
Na = Hcos+ usin
Rx = Ucos - HsinQ
= 
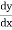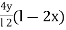
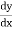= tan =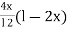 
= tan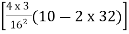 
= 29˚21’
Rx = 12.cos 29l I – 160sin 29.21
Rx = 26.1 J KN
N = 160cos29.21˚+ 120sin29.21’
N = 198.28kn
Key takeaways:
Step 1) Find reaction components
Step 2) Find normal thrust and radial shear at any section
Step 3) Find B.M at any section
References:
1. Hibbler, “Structural Analysis”, Pearson Education
2. Mau, “Introduction to Structural Analysis” CRC Press Taylor & Francis Group.
3. Ghali, “Structural Analysis: A Unified Classical and Matrix Approach” 5/e, CRC Press Taylor & Francis Group.
4. T S Thandavmorthy, “Analysis of Structures”, Oxford University Press 5. Wilbur and Norris, “Elementary Structural Analysis”, Tata McGraw Hill.
5. Timoshenko & Young “Theory of Structure” Tata Mc Grew Hill.
6. Reddy, CS, “Basic Structural Analysis”, Tata McGraw Hill.
7. Jain, OP and Jain, BK, “Theory & Analysis of Structures”. Vol. I & II Nem Chand.
8. Vazirani & Ratwani et al, “Analysis of Structures”, Khanna Publishers
