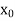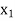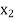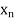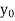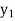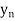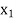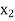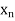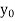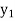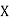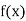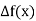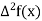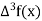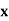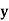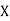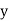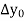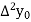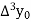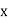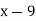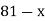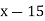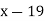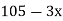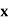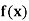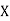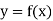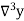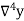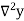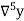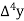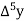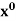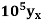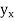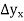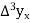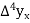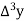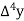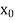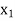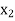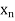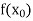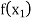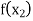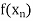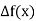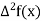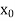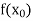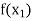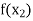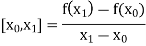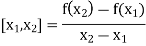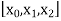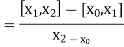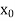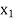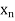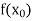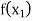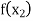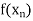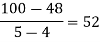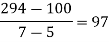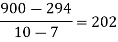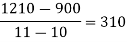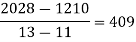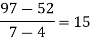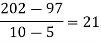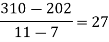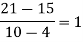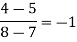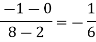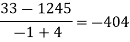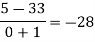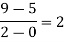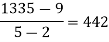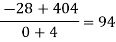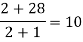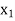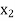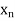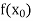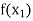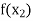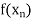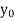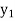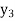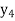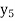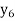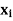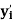Unit-2
Interpolation
Interpolation
Definition: Interpolation is a technique of estimating the value of a function for any intermediate value of the independent variable while the process of computing the value of the function outside the given range is called extrapolation.
Let 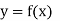 be a function of x.
be a function of x.
The table given below gives corresponding values of y for different values of x.
X |
|
| | …. |
|
y= f(x) |
|
|
| …. |
|
The process of finding the values of y corresponding to any value of x which lies between 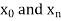 is called interpolation.
is called interpolation.
If the given function is a polynomial, it is polynomial interpolation and given function is known as interpolating polynomial.
Conditions for Interpolation
1) The function must be a polynomial of independent variable.
2) The function should be either increasing or decreasing function.
3) The value of the function should be increase or decrease uniformly.
Finite Difference
Let  be a function of x. The table given below gives corresponding values of y for different values of x.
be a function of x. The table given below gives corresponding values of y for different values of x.
X |
|
| | …. |
|
y= f(x) |
|
|
| …. |
|
a) Forward Difference: The  are called differences of y, denoted by
are called differences of y, denoted by 
The symbol 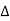 is called the forward difference operator. Consider the forward difference table below:
is called the forward difference operator. Consider the forward difference table below:
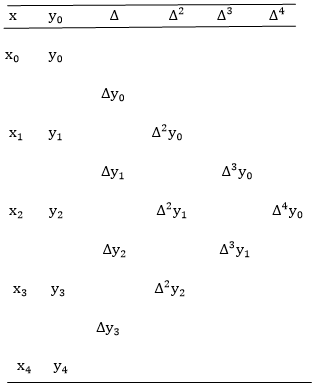
Where 
And 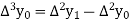 third forward difference so on.
third forward difference so on.
b) Backward Difference:
The difference 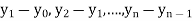 are called first backward difference and is denoted by
are called first backward difference and is denoted by 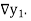 Consider the backward difference table below:
Consider the backward difference table below:

Where 
And 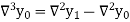 third backward differences so on.
third backward differences so on.
Key takeaways-
a) Forward Difference: The  are called differences of y, denoted by
are called differences of y, denoted by 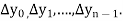
The symbol 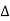 is called the forward difference operator
is called the forward difference operator
3. Backward Difference:
The difference 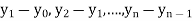 are called first backward difference and is denoted by
are called first backward difference and is denoted by 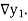
Newton Forward Difference formula:
This method is useful for interpolation near the beginning of a set of tabular values.
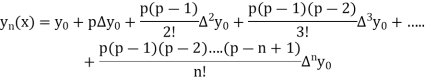
Where 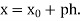
Example1: Using Newton’s forward difference formula, find the sum
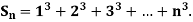
Putting 
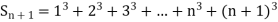

It follows that
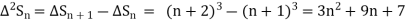
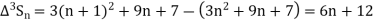
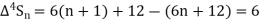
Since  is a fourth degree polynomial in n.
is a fourth degree polynomial in n.
Further,
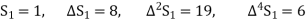
By Newton Forward Difference Method
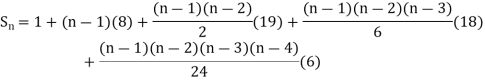
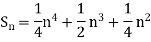
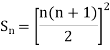
Example2: Given 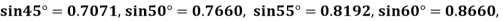 find
find 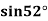 , by using Newton’s forward interpolation method.
, by using Newton’s forward interpolation method.
Let  , then
, then
|
|
|
|
|
|
| 0.7071 | 0.7660 | - | 0.8192 | 0.8660 |
The table of forward finite difference is given below:
|
|
|
|
|
45
50
55
60 | 0.7071
0.7660
0.8192
0.8660 |
0.0589
0.0532
0.0468 |
-0.0057
-0.0064 |
-0.0007 |
By Newton’s forward difference method
Here initial value 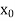 = 45, difference of interval h = 5 and the value to be calculated at x=52.
= 45, difference of interval h = 5 and the value to be calculated at x=52.
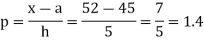
By Formula
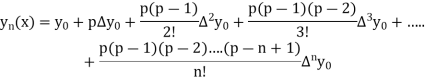
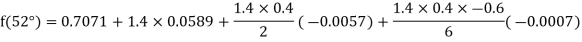
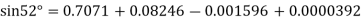

Example3: Find the missing term in the following:
| 0 | 1 | 2 | 3 | 4 |
| 1 | 3 | 9 | ? | 81 |
Let 
First, we construct the forward difference table:
|
|
|
|
|
0
1
2
3
4 | 1
3
9
81 |
2
6
|
4
|
|
Now, 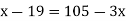


Newton Backward Difference Method:
This method is useful for interpolation near the ending of a set of tabular values.
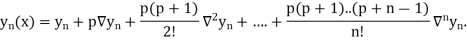
Where 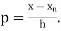
Example1: Find 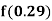 from the following table:
from the following table:
| 0.20 | 0.22 | 0.24 | 0.26 | 0.28 | 0.30 |
| 1.6596 | 1.6698 | 1.6804 | 1.6912 | 1.7024 | 1.7139 |
Consider the backward difference method
|
|
|
|
|
|
|
0.20
0.22
0.24
0.26
0.28
0.30 | 1.6596
1.6698
1.6804
1.6912
1.7024
1.7139 |
0.0102
0.0106
0.0108
0.0112
0.0115 |
0.0004
0.0002
0.0004
0.0003 |
-0.0002
0.0002
-0.0001 |
0.0004
-0.0003 |
-0.0007 |
Here 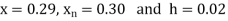
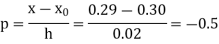
By Newton backward difference formula

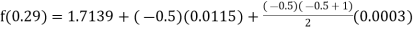
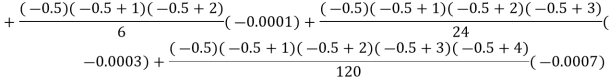
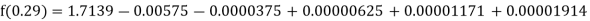
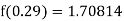
Example2: The following table give the amount of a chemical dissolved in water:
Temp. |
|
|
|
|
|
|
Solubility | 19.97 | 21.51 | 22.47 | 23.52 | 24.65 | 25.89 |
Compute the amount dissolve at 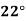
Consider the following backward difference table:
Temp. x | Solubility y |
|
|
|
|
|
10
15
20
25
30
35 | 19.97
21.51
22.47
23.52
24.65
25.89 |
1.54
0.96
1.05
1.13
1.24 |
-0.58
0.09
0.08
0.11 |
0.67
-0.01
0.03 |
-0.68
0.04 |
0.72 |
Here 
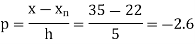
By Newton Backward difference formula
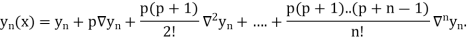
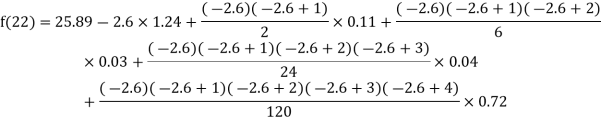

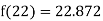
Example3: The following are the marks obtained by 492 candidates in a certain examination
Marks | 0-40 | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 |
No. of candidates | 210 | 43 | 54 | 74 | 32 | 79 |
Find out the number of candidates:
a) Who secured more than 48 but not more than 50 marks?
b) Who secured less than 48 but not less than 45 marks?
Consider the forward difference table given below:
Marks up to x | No. of candidates y |
|
|
|
|
|
40
45
50
55
60
65 | 210
210+43=253
253+54=307
307+74=381
381+32=413
413+79= 492 |
43
54
74
32
79 |
11
20
-42
47 |
9
-62
89 |
-71
151 |
222 |
Here 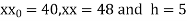
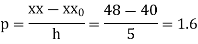
By Newton Forward Difference formula
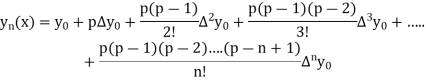
f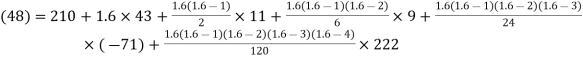
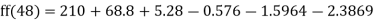
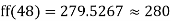
a) No. of candidate secured more than 48 but not more than 50 marks
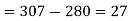
b) No. of candidate secured less than 48 but not less than 45 marks
Key takeaways-
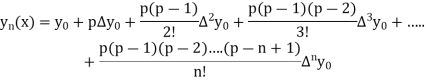
Where 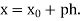
2. Newton Backward Difference Method:
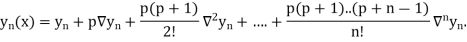
Where 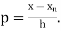
Gauss forward difference formula-
The Gauss forward difference formula is defined as-
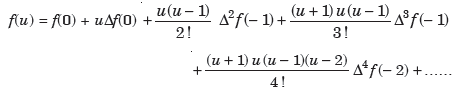
Gauss backward difference formula-
The Gauss backward difference formula is defined as-
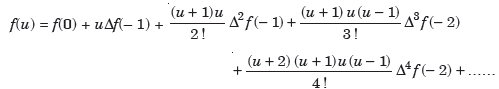
Example: By using Gauss forward difference formula obtain f (32) given that-
f (25) = 0.2707 f (35) = 0.3386
f (30) = 0.3027 f (40) = 0.3794
Sol.
Here
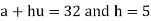
Let us take the origin at 30, a = 30 then we get-
u = 0.4
The forward difference table-
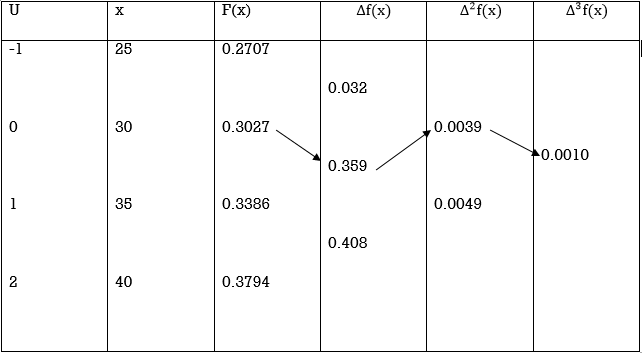
By using Gauss forward difference formula, we get-
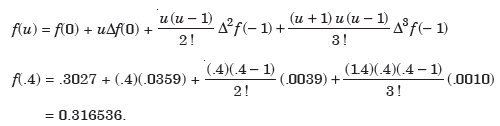
Example: Find  by using Gauss forward formula if-
by using Gauss forward formula if-
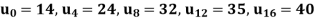
Sol.
Let a = 8, h = 4,
We have
a + hu = 9
and we get-
u = 0.25
The forward difference table-

By using Gauss forward difference formula, we get-
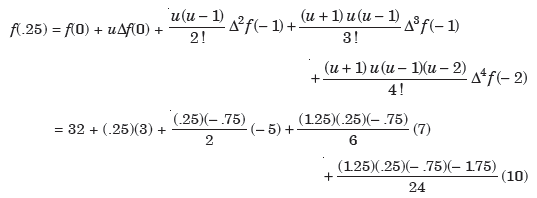
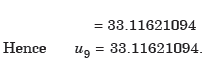
Example: Using Gauss’s backward interpolation formula, find the population for the year 1936 given that-
Year | 1901 | 1911 | 1921 | 1931 | 1941 | 1951 |
Population (in thousands) | 12 | 15 | 20 | 27 | 39 | 52 |
Sol.
Let origin is at 1941 and h = 10
Then-
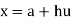
Which gives-
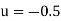
The backward difference table-
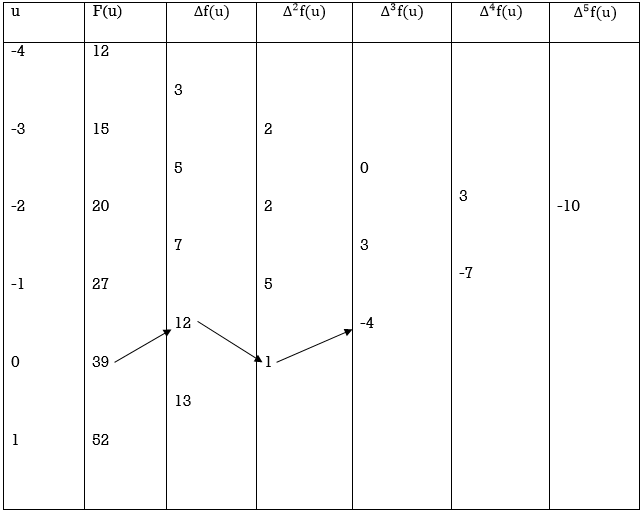
By using Gauss backward formula, we get-
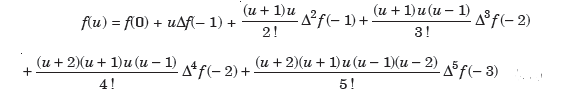

Hence the pop. of the year 1936 is 32625
Key takeaways-

2. Gauss backward difference formula-
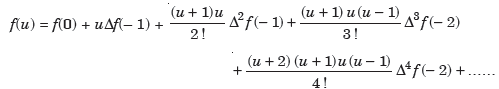
Stirling’s formula-
The Stirling’s formula is the average of Gauss forward and backward interpolation formulae.
It is defined as-

Bessel’s formula-
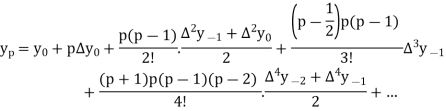
Example: By using Stirling’s formula to compute  from the table (
from the table (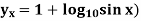 given below-
given below-
| 10 | 11 | 12 | 13 | 14 |
| 23,967 | 28,060 | 31,788 | 35,209 | 38,368 |
Sol.
Taking the origin at 
We get the following central table-
P |
|
|
|
|
|
-2
-1
0
1
2 | 0.23967
0.28060
0.31788
0.35209
0.38368 |
0.04093
0.03728
0.034121
0.03159 |
-0.00365
-0.00307
-0.00062 |
0.00058
-0.00045 |
-0.00013
|
At x = 12.2, p = 0.2
Stirling’s formula-
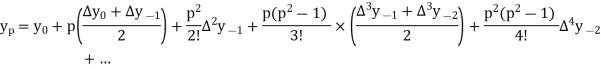
When p = 0.2, we get-
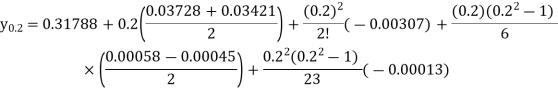
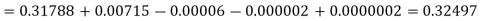
Example: By using Bessel’s formula to find the value of f (27.5) from the table given below-
x | 25 | 26 | 27 | 28 | 29 | 30 |
f(x) | 4.000 | 3.846 | 3.704 | 3.571 | 3.448 | 3.333 |
Sol.
Taking the origin at 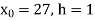
We have p = x – 27
The central table will be as follows-
x | P | Y |
|
|
|
|
25
26
27
28
29
30 | -2
-1
0
1
2
3 | 4.000
3.846
3.704
3.571
3.448
3.333 |
-0.154
-0.142
-0.133
-0.123
-0.115
|
0.012
0.009
0.010
0.008 |
-0.003
-0.001
-0.002 |
0.004
-0.001 |
At x = 27.5, p =0.5
Bessel’s formula is-

When p = 0.5, we get-
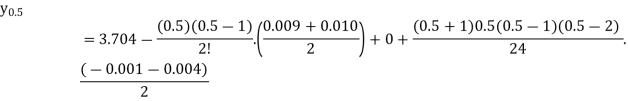

So that-
f (27.5) = 3.585
Example: Using Everett’s formula, evaluate f (30) if
f (20) = 2854, f (28) = 3162
f (36) = 7088, f (44) = 7984.
Sol.
Let the origin is 28, a = 28, h = 8
Then
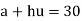
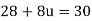
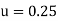
And
The difference table is-
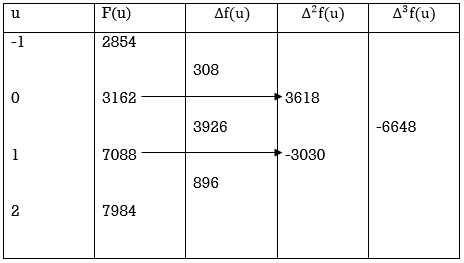
By using Everette’s formula-
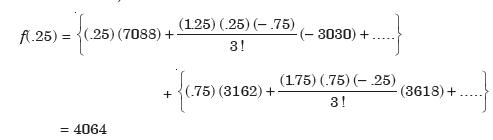
Therefore f (30) = 4064
Key takeaways-

2. Bessel’s formula-
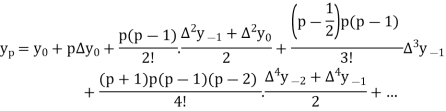
Divided Difference:
In the case of interpolation, when the value of the argument is not equi-spaced (unequal intervals) we use the class of differences called divided differences.
Definition: The difference which are defined by taking into consideration the change in the value of the argument is known as divided differences.
Let 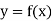 be a function defined as
be a function defined as
|
|
| ……. |
|
|
|
|
………… |
|
Where 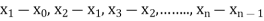 are unequal i.e., it is case of unequal interval.
are unequal i.e., it is case of unequal interval.
The first order divided differences are:
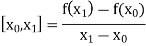
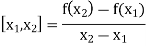
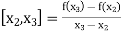 And so on.
And so on.
The second order divided difference is:
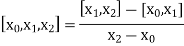
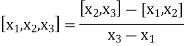
 And so on.
And so on.
Similarly, the nth order divided difference is:

With the help of these we construct the divided difference table:
X | f(x) |
|
|
|
|
|
|
Newton’s Divided difference Formula:
Let  be a function defined as
be a function defined as
|
|
| ……. |
|
|
|
|
………… |
|
Where 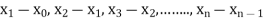 are unequal i.e., it is case of unequal interval.
are unequal i.e., it is case of unequal interval.
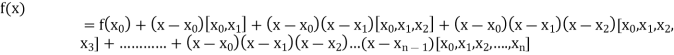 .
.
Example1: By means of Newton’s divided difference formula, find the values of 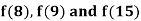 from the following table:
from the following table:
X | 4 | 5 | 7 | 10 | 11 | 13 |
f(x) | 48 | 100 | 294 | 900 | 1210 | 2028 |
We construct the divided difference table is given by:
x | f(x) | First order divide difference | Second order divide difference | Third order divide difference | Fourth order divide difference |
4
5
7
10
11
13 | 48
100
294
900
1210
2028 |
|
|
|
0
0 |
By Newton’s Divided difference formula
 .
.
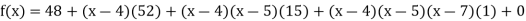
Now, putting 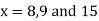 in above we get
in above we get
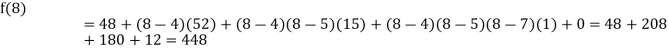 .
.
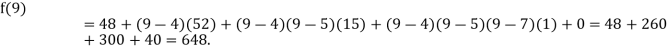
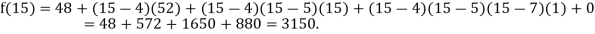
Example2: The following values of the function f(x) for values of x are given:
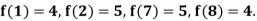
Find the value of 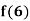 and also the value of x for which f(x) is maximum or minimum.
and also the value of x for which f(x) is maximum or minimum.
We construct the divide difference table:
x | f(x) | First order divide difference | Second order divide difference | Third order divide difference |
1
2
7
8 | 4
5
5
4 |
|
|
0 |
By Newton’s divided difference formula
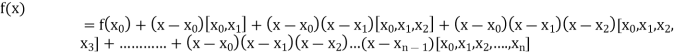 .
.
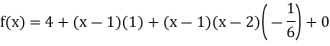
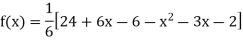
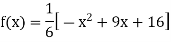
Putting 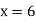 in above we get
in above we get
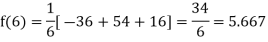
For maximum and minimum of 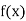 , we have
, we have
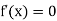
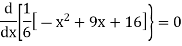
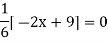
Or 
Example3: Find a polynomial satisfied by
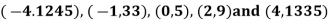 , by the use of Newton’s interpolation formula with divided difference.
, by the use of Newton’s interpolation formula with divided difference.
x | -4 | -1 | 0 | 2 | 4 |
F(x) | 1245 | 33 | 5 | 9 | 1335 |
Here
We will construct the divided difference table:
x | F(x) | First order divided difference | Second order divided difference | Third order divided difference | Fourth order divided difference |
-4
-1
0
2
4 | 1245
33
5
9
1335 |
|
|
|
|
By Newton’s divided difference formula
 .
.
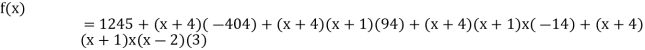

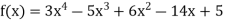
This is the required polynomial.
Lagrange’s Interpolation of polynomial:
Let  , be defined function we get
, be defined function we get
X |
|
|
| ….. |
|
f(x) |
|
|
| …… |
|
Where the interval is not necessarily equal. We assume f(x) is a polynomial od degree n. Then Lagrange’s interpolation formula is given by
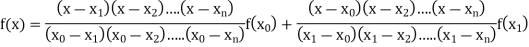
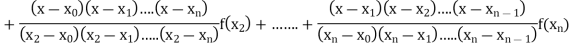
Example1: Deduce Lagrange’s formula for interpolation. The observed values of a function are respectively 168,120,72 and 63 at the four position3,7,9 and 10 of the independent variables. What is the best estimate you can for the value of the function at the position6 of the independent variable?
We construct the table for the given data:
X | 3 | 6 | 7 | 9 | 10 |
Y=f(x) | 168 | ? | 120 | 72 | 63 |
We need to calculate for x = 6, we need f(6)=?
Here 
We get 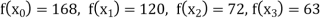
 By Lagrange’s interpolation formula, we have
By Lagrange’s interpolation formula, we have
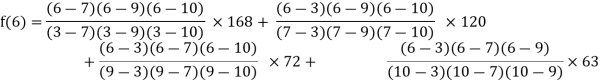
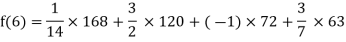
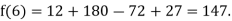
Hence the estimated value for x=6 is 147.
Example2: By means of Lagrange’s formula, prove that
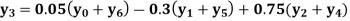
We construct the table:
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
Y=f(x) |
|
|
|
|
|
|
|
Here x = 3, f(x)=?
 By Lagrange’s formula for interpolation
By Lagrange’s formula for interpolation
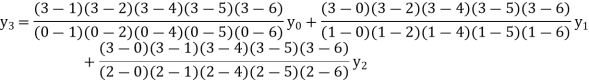
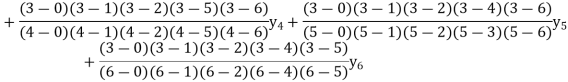
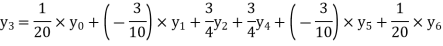

Hence proved.
Example3: Find the polynomial of fifth degree from the following data
X | 0 | 1 | 3 | 5 | 6 | 9 |
Y=f(x) | -18 | 0 | 0 | -248 | 0 | 13104 |
Here 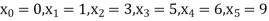
We get 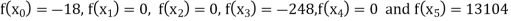
 By Lagrange’s interpolation formula
By Lagrange’s interpolation formula
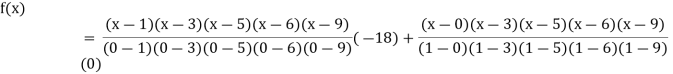
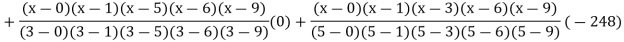


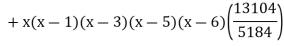
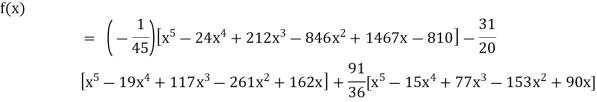
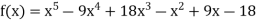
Hermite’s interpolation formula-
The Hermite’s interpolation formula is defined as-
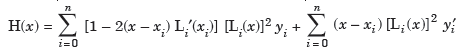
Example: Find the cubic polynomial by using Hermite’s interpolation formula, given-
|
|
|
0 | 0 | 0 |
1 | 1 | 1 |
Sol.
We know that Hermite’s interpolation formula-

 ..........(1)
..........(1)
Now
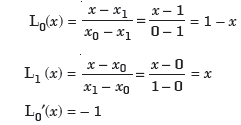
And

Hence
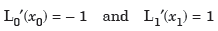
From equation (1)-
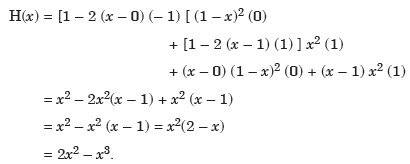
Key takeaways-
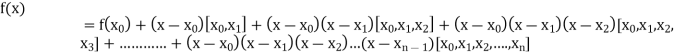 .
.
3. Hermite’s interpolation formula
References