2.1 Crosssectional elements | unit 2 geometric designirc73 latest revision

Unit-2

Geometric Design

The features of the cross-section of the pavement influence the life of the pavement as well as the riding comfort and safety.

Carriageway

Shoulder

Roadway Width

Right of Way

Building Line & Control Line

Median

Camber

Side Slope

Lateral and Vertical Clearances

Kerb

Guard Rail

Side Drain

Other Facilities

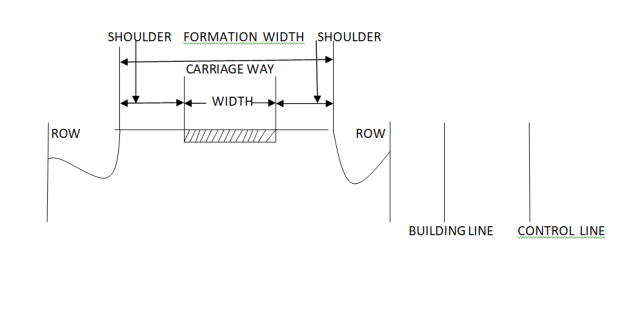
$C:\Users\Ssd\Desktop\Untitled 6.png$

Fig.1: Cross-section of Roads

Key Takeaways:

Right of way: - A right-of-way (ROW) is a right to make a way over a piece of land, usually to and from another piece of land.

Roadway Width: - In particular, the width of the standard road lane in the United States is specified to be 3.7 m for the interstate highway systems, while the narrower lanes are used on lower classification roads. In Europe, the road and lane width vary by country, but the minimum width of the lane is generally from 2.5 to 3.25 m.

2.2 Camber

Camber or Cant is the cross slope provided to raise the middle of the road surface in the transverse direction to drain rainwater from the road surface.

The objectives of providing the camber are

Surface protection (especially for gravel and bituminous roads)
Subgrade protection (by proper drainage)
Quick-drying of pavement which in turn increases safety

Depending on the type of road surface and amount of rainfall, the following camber is suggested by IRC:

Surface Type	Heavy Rain	Light Rain
Concrete/Bituminous	2%	1.7%
Gravel/WBM	3%	2.5%
Earthen	4%	3%

Excessive camber or cross slope should be avoided because

Excessive camber will cause a transverse tilt of the vehicle making it uncomfortable for passengers. Also, the distribution of load to different wheels will not be uniform, leading to uneven wear and tear of wheels and damage to pavements.
With excessive camber, heavy rain will result in the formation of heavy cross ruts.
The central seeking tendency of vehicles will increase to avoid transverse tilt.

Different types of Camber:

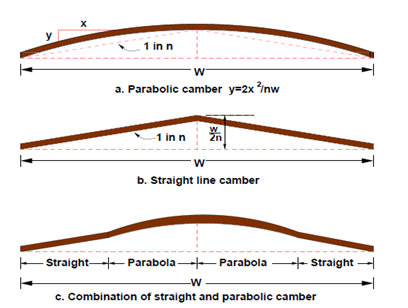
Parabolic Camber
Straight Line Camber
Combination of Straight and Parabolic Camber

Fig.2: Types of camber

Key Takeaways:

Parabolic camber: - Parabolic camber is provided by providing a parabolic shape to the surface of the road. It is also not used in general because it has steep slopes towards the edges, which can create an outward thrust to the vehicles.

Straight Line camber: - Normally, the camber is provided on the straight roads by raising the center of the carriageway with respect to these edges, forming a crown or highest point on the center-line.

2.3 Shoulder

Shoulders are provided along the road edge and are intended for accommodation of stopped vehicles, serve as an emergency lane for vehicles, and provide lateral support for base and surface courses.

Shoulders support the carriageway.

Minimum width of 2.5 m is recommended for 2-lane rural highways in India.

Key Takeaways:

Formation Width: - Width of formation or roadway width is the sum of the widths of pavements or carriageway including separators and shoulders. This does not include the extra land in the formation/cutting.

Carriageway width: - A minimum width of 2.5 m is recommended for 2-lane rural highways in India. Parking lanes are provided in urban lanes for side parking.

2.4 Sight distance

The safe and efficient operation of vehicles on the road depends very much on the visibility of the road ahead of the driver. Thus the geometric design of the road should be done such that any obstruction on the road length could be visible to the driver from some distance ahead. This distance is said to be the sight distance.

For straight road on level ground, there is no problem of side distance. But Straight road on level ground is a rare case. Horizontal curves, vertical curves (Summit), intersections are potential places where there could be a restriction in terms of Sight distance

The actual distance along the road surface over which a driver from a specified height above the carriageway has visibility of the stationary or moving object.

The sight distance used for design are

Stopping Sight Distance (SSD) or absolute minimum sight distance

Intermediate Sight Distance (ISD) = 2*SSD

Overtaking Sight Distance (OSD) for safe overtaking

Headlight Sight Distance = SSD at night

Key takeaways:

Intermediate sight distance: -Intermediate sight distance (ISD) is defined as twice SSD. Overtaking sight distance (OSD) for safe overtaking operation. Headlight sight distance is the distance visible to a driver during night driving under the illumination of headlights.

Overtaking sight distance: -The overtaking sight distance is the minimum distance open to the vision of the driver of a vehicle intending to overtake the slow vehicle ahead safely against the traffic in the opposite direction.

Headlight sight distance: -Headlight sight distance is the distance visible to a driver during night driving under the illumination of headlights.

2.5 Horizontal curves

Horizontal alignment design involves the understanding of the design aspects such as design speed and the effect of the horizontal curve on the vehicles.

The horizontal curve design elements include the design of superelevation, extra widening at horizontal curves, design of transition curve, and set back distance.

The presence of a horizontal curve imparts centrifugal force which is a reactive force acting outward on a vehicle negotiating it. The centrifugal force depends on the speed and radius of the horizontal curve and is counteracted to a certain extent by transverse friction between the tyre and pavement surface.

On a curved road, this force tends to cause the vehicle to overrun or to slide outward from the center of road curvature.

2.5.1 Forces acting on a Vehicle on Horizontal Curve

b: Distance between two wheels or total width of the wheelbase

h: height of the center of gravity of vehicle above the road surface

W: Weight of Vehicle

P: Centrifugal Force acting outwards

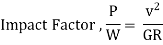
The vehicle overturns the w.r.t. outer wheel due to Centrifugal Force. On the verge of overturning, the contact between the inner tyre and road will be lost.

Overturning:

= Resistance Against Overturning

Lateral Skid: Can be avoided by increasing friction at curves

P=F

P =f*W

f: Coefficient of Lateral Friction = 0.15

Key Takeaways: -

Overturning: - Overturning occurs on the roads when the trucks try to change directions, take sharp turns. Overturning occurs, more after, in the case of vehicles that have a greater height or whose center of gravity is much high up from the surface of roads.

Lateral Skid: - If a vehicle skids, it slides sideways or forwards while moving, for example, when ... It just tipped over onto its side and skidded along the tarmac.

Centrifugal Force: - Centrifugal force is the apparent outward force on a mass when it is rotated. Think of a ball on the end of a string that is being twirled around, or the outward motion you feel when turning a curve in a car.

2.6 Super elevation

To counter the effect of centrifugal force and to reduce the tendency of the vehicle to overturn or skid, the outer edge of pavement is raised w.r.t. inner edge. The transverse inclination of the pavement surface is known as ‘Super elevation’.

Fig.3: Vehicle on a sloping road

With Super elevation parallel to the road surface, a component of centrifugal force will be acting and a component of weight (because of super elevation) will be resisting the centrifugal force.

Super elevation e = tanθ

v: Speed in m/s

e: Rate of super elevation or angle of super elevation

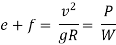
2.6.1 Equilibrium Super elevation or Balanced S.E.

Normally, the centrifugal force is supposed to be balanced by super elevation along with the coefficient of lateral friction.

If f=0, then the entire centrifugal force is balanced by super elevation alone. This super elevation is known as Equilibrium or Balanced Super elevation.

With equilibrium super elevation, the pressure on the inner and outer tyre will be the same as that of a vehicle moving on a straight road (without super elevation).

But since only Super elevation counteracts centrifugal force, this results in a very high value of super elevation. So, super elevation along with friction is preferred.

Equilibrium super elevation is best suited for vehicles moving with design speed.

If the vehicles are moving slowly over the curve with Equilibrium Super elevation, there is a chance of skidding or overturning inwards. So, equilibrium super elevation is not practically used.

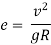
2.6.2 Maximum and Minimum Super elevation [IRC]

Terrain	emax
Plain and Rolling Terrain	7%
Hilly Terrain [Snow Bound]	7%
Hilly Terrain [Not Bound by Snow]	10%

Camber and Super elevation both are cross slope. Camber is for drainage purposes; the cross slope is for countering centrifugal force.

If the calculated super elevation is less than or equal to camber, then Super elevation equal to camber should be provided from drainage consideration. Else, drainage problems might be there affecting the pavement surface quality.

2.6.3 (3/4)th Design Speed Assumption

If the super elevation is provided for design speed, then it will be convenient for vehicles moving with less than design speed.

So, the question is whether super elevation should fully counteract the centrifugal force or only a fixed portion of centrifugal force. In the former case, super elevation needed would be more than 7% on sharp curves causing inconvenience to slow-moving vehicles.

When a vehicle negotiates a flat curve, friction would not be developed to the maximum, so this is not a balanced design.

So, the super elevation should be such that a moderate amount of friction is developed while negotiating flat curves and friction not exceeding maximum allowable value developed at a sharp curve.

Indian Practice: Super elevation should counteract centrifugal force developed by 3/4th design speed. v = 75% of Design Speed, f=0

Design speed in KMPH as per IRC (ruling and minimum)

Type	Plain	Rolling	Hilly	Steep
NH & SH	100-80	80-65	50-40	40-30
MDR	80-65	65-50	40-30	30-20
ODR	65-50	50-40	30-25	25-20
VR	50-40	40-35	25-20	25-20

2.6.4 Design Super elevation:

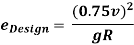
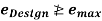[Given by IRC based on terrain or topography]

Friction Factor:

IRC recommends the coefficient of lateral friction as 0.15.
Friction factor also depends on various factors like
- Speed of vehicle
- Type and condition of the road surface.
- Type and condition of a vehicle tyre

2.6.5 Super elevation with or without Transition Curves

Super elevation should be attained gradually over the full length of the transition curve so that the design Super elevation is available at the starting point of the circular portion.

When due to some reasons the transition curve cannot be provided, 2/3rdSuperelevation may be attained on the straight portion (tangent) and balanced 1/3rd on the curve.

2.6.6 Ruling and Minimum Radius of Horizontal Curves:

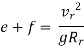
For a particular speed, the centrifugal force is dependent on the radius of the horizontal curve.

Ruling radius R based on ruling design speed vr

3. Absolute Minimum radius Rmin based on ruling design speed vmin

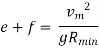
2.6.7 Attainment of Super elevation

Elimination of crown of the cambered section

Rotation of pavement to attain full Super elevation.

Elimination of Crown of Cambered Section

Outer edge rotated about the crown

Fig.4: Outer edge rotation

Disadvantage:

After a full rotation, we have a slope at the outer edge equal to the camber. But in between, for a small length of the road, the cross slope is less than camber.
Drainage problem in outer half and outer edge in that portion may be damaged easily.

b. Crown Shifted Outward

Fig.5: Crown Shifted

Disadvantage:

Large negative Super elevation on the outer half
Drivers tend to run the vehicle along with the shifted crown.

2. Rotation of Pavement to attain full Super elevation:

Rotation w.r.t. Center Line:

Depressing the inner edge and raising the outer edge each by half the total amount (E) of Super elevation.

Fig.6: Rotation with respect to the center line

Advantage:

Earthwork is balanced (cut and fill balanced)
The vertical profile remains unchanged.

Disadvantage:

Drainage problem because of depressing the inner edge below the general level.

b. Rotation w.r.t. Inner Edge:

Raising both the center as well as the outer edge.

Disadvantage:

Additional earth filling.
The centerline of the road is also raised, so the vertical alignment of the road is also changed.

c. Rotation w.r.t. Outer Edge:

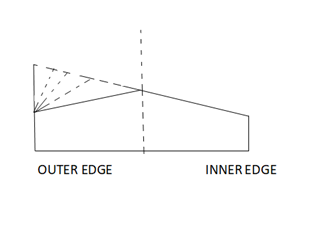
Not recommended due to drainage problem.

Fig.7: Rotation with respect to the outer edge

2.6.8 Steps Involved in Super elevation Calculation:

Basic Super elevation Equation: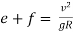

For Mixed Traffic Condition,

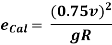
Step 1: Calculate Super elevation for 75% of Design Speed

Step 2: If ecal<emax, Provide ecal

If ecal>emax, provide emaxand proceed with step 3 & 4.

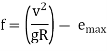
Step 3: Check coefficient of friction developed f with emax at full value of design speed.

If the value of f thus calculated is less than 0.15, then OK, else calculate the restricted speed as given in step 4.

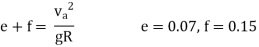
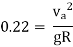
Step 4: Calculate allowable speed Va

Either restrict or reduce the speed or provide a better or more radius of the horizontal curve.

Key Takeaways:

Super elevation: - Super elevation is the transverse slope provided to counteract the effect of centrifugal force and reduce the tendency of the vehicle to overturn and to skid laterally outwards by raising the pavement outer edge with respect to the inner edge.

2.7 Extra widening

Extra widening refers to the additional width of carriageway that is required on a curved section of a road over and above that is required on a straight alignment.

This widening is done due to two reasons: the first and most important is the additional width required for a vehicle taking a horizontal curve and the second is due to the tendency of the drivers to ply away from the edge of the carriageway as they drive on a curve.

The first is referred to as the mechanical widening and the second is called the psychological widening.

1. Mechanical Widening:

When a vehicle negotiates a horizontal curve, the rear wheels follow a path of a shorter radius than the front wheels. This phenomenon is called off tracking and has the effect of increasing the effective width of a road space required by the vehicle.

Therefore, to provide the same clearance between vehicles traveling in the opposite direction on curved roads as is provided on straight sections, there must be an extra width of carriageway available.

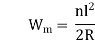
Where,

Wm = Mechanical Widening

n = Number of Lanes

R = Radius of Curve

2. Psychological Widening:

There is a tendency for the drivers to drive close to the edges of the pavement on curves. Some extra space is to be provided for more clearance for the crossing and overtaking operations on curves.

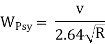
Key Takeaways:

The radius of the curve: - The minimum curve radius is a limiting value of curvature for a given design speed. In the design of horizontal alignment, smaller than the calculated boundary value of minimum curve radius cannot be used.

2.8 Transition curves and gradient

The transition curve is provided to change the horizontal alignment from straight to circular curve gradually and has a radius that decreases from infinity at the straight end (tangent point) to the desired radius of the circular curve at the other end (curve point).

The rate of change of radius of the transition curve depends on the shape and equation of the curve.

Fig.8: Transition Curve

2.8.1 Necessity of Transition Curve

Introduce gradually the centrifugal force between the tangent point and the beginning of the circular curve avoiding a sudden jerk on the vehicle.

Enable the driver to turn the steering gradually with comfort and safety (easy to follow the path for drivers).

Minimize encroachment on adjoining traffic lanes tend to promote uniformity in speed.

Enable gradual introduction of designed super elevation

Enable the gradual introduction of required extra widening.

Improve the aesthetic appearance of the road.

2.8.2 Different Types of Transition Curves:

Cubic Parabola

Lemniscates

Spiral (Clothoid)

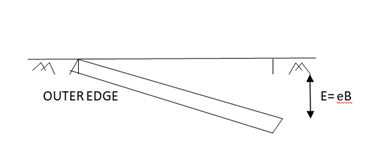
Fig.9: Different transition curve

Up to a deflection angle of 9 degrees, there is no significant difference in these curves.

Radius decreases with an increase in length for all these curves.

Lemniscates and Cubic Parabola: Rate of change of radius and hence rate of change of centrifugal acceleration is not constant for large deflection angle.

Spiral: Radius is inversely proportional to the length and the rate of change of centrifugal acceleration is uniform throughout the length of the curve.

2.8.3 Ideal Shape of Transition Curves:

The rate of introduction of centrifugal force or rate of change of centrifugal acceleration should be consistent.

The length should be inversely proportional to the radius.

Spiral fulfills the condition of an ideal transition curve.

The geometric property of the spiral is such that the calculations and setting out of the curve in the field are simple and easy (LR= constant).

The spiral transition curve simulates the natural turning path of a vehicle.

2.8.4 Design Criteria:

Centrifugal Force / Comfort Criteria

Ls: Length of Transition Curve

v: Speed in m/s

R: Radius of Horizontal Curve in m

C: Rate of change of Centrifugal Acceleration in m/s3

V: Speed in KMPH

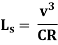
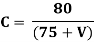
B. Based on Rate of Change of Super elevation:

Longitudinal grade developed at the pavement edge compared to through grade along the centerline.

The rate of change should not cause discomfort to travelers or make the road appear unsightly.

Rate of Change [Limiting Value/Minimum Value]

Plain and Rolling Terrain: 1 in 150
Mountainous or Steep Terrain: 1 in 60

The required length depends on the method of attainment of Superelevation.

Ls = N * E

= N* eB

B: Width of Pavement depending on the method of rotation of pavement.

Ls = N *e*(w+we)_____[ Pavement Rotation w.r.t. Inner Edge]

w: Normal width of Pavement

we: Extra Widening on a circular curve

1 in N: rate of change of Superelevation

C. Empirical Formula Based on the Recommended Maximum Rate of Change of Super elevation:

For Plain and Rolling Terrain

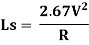
V: Speed in KMPH

ii. Mountainous and Steep or Hilly Terrain

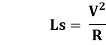
The shift of Curve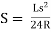

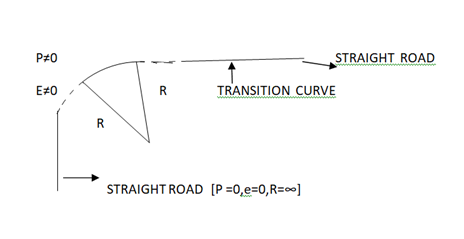
2.8.5 Gradient

The gradient is the rate of rising or fall along the length of the road with respect to the horizontal. It is expressed as a ratio of 1 in x (1 vertical unit to x horizontal units). Sometimes it is also expressed as % i.e. n in 100.

The ascending gradients are given a positive sign and are denoted as +n1, +n2, etc. The descending Gradients are given a negative sign and are denoted as –n3, -n4,etc.

The angle which measures the change of direction at the intersection of two grades is called the deviation angle N which is equal to the algebraic difference between the two grades.

Fig.10: Different gradient

While aligning a highway, the gradient is decided for designing the vertical curve. Before finalizing the gradients, the construction cost, vehicular operation cost, and the practical problems in the site also have to be considered.

2.8.6 Types of Gradient

1. Ruling Gradient

The ruling gradient or the design gradient is the maximum gradient with which the designer attempts to design the vertical profile of the road.

This depends on the terrain, length of the grade, speed, pulling power of the vehicle, and the presence of the horizontal curve.

The ruling gradient is adopted by the designer by considering a particular speed as the design speed and for a design vehicle with standard dimensions. But traffic in India is heterogeneous in nature and hence it is not possible to lay down precise standards for the country as a whole.

Hence IRC has recommended some values for the ruling gradient for different types of terrain.

Terrain	Ruling Gradient
Plain and Rolling Terrain	1 in 30
Mountainous Terrain	1 in 20
Steep Terrain	1 in 16.7

2. Limiting Gradient

These are steeper than the Ruling gradient and adopted when the ruling gradient results in an enormous increase in the cost of construction.

On rolling terrain and hilly terrain, it may be frequently necessary to adopt a limiting gradient. But the length of the limiting gradient stretches should be limited and must be sandwiched by either straight roads or easier grades.

Limiting Gradient depends on

Topography
Cost

3. Exceptional Gradient

These are given in unavoidable situations and should be limited for short stretches not exceeding about 100 meters at a stretch.

In mountainous and steep terrain, successive exceptional gradients must be separated by a minimum 100-meter length gentler gradient.

At hairpin bends, the gradient is restricted to 2.5%.

4. Minimum Gradient

This is important only at locations where surface drainage is important. Camber will take care of the lateral drainage. But the longitudinal drainage along the side drains requires some slope for smooth flow of water.

Therefore, the minimum gradient is provided for drainage purposes and it depends on the rainfall, type of soil, and other site conditions.

A minimum of 1 in 500 may be sufficient for concrete drain and 1 in 200 for open soil drains are found to give satisfactory performance.

Ruling < Gradient

Limiting < Gradient

Exceptional < Gradient

Minimum Gradient

Key Takeaways:

Transition curve: - A transition curve may be defined as a curve of the varying radius of infinity at the tangent point to a design circular curve radius provided in between the straight and circular path in order that the centrifugal force was gradual.

Gradient: - It is the rate of rising or fall of road level along its length. It is expressed either as the rate of rising or fall to the horizontal distance or as percentage rise or fall. In India usually, former practice is used.

2.9 Vertical curves

Vertical curves facilitate a gradual change between two different gradients.

Vertical curves should be simple in application and result in a design that is safe and comfortable in operations, pleasing in appearance, and adequate for drainage.

Types of Vertical Curves:

Summit Curves
Valley Curves

Key takeaways:

Summit Curve: - Summit curves are those curves that have convexity upwards.

Valley Curve: - Valley curve or sag curves are vertical curves with convexity downwards.

2.10 Summit and valley curves

2.10.1 Summit Curves

Summit curves or crest curves are convex upwards.

If Deflection Angle N is Positive, the vertical curve is Summit Curve.

If the road surface is below the point of vertical intersection, then it is a summit curve

Fig.11: Summit curve

Summit Curves are formed when two gradients meet as illustrated below:

when an ascending gradient meets a descending gradient

when a positive gradient meets a flat gradient

when a steep ascending gradient meets a relatively mild gradient

when a flat gradient meets a descending gradient

when a mild descending grade meets a steeper descending gradient

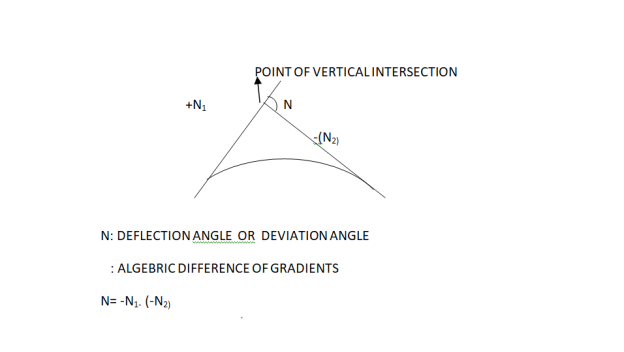
$C:\Users\Ssd\Desktop\Untitled 8.png$

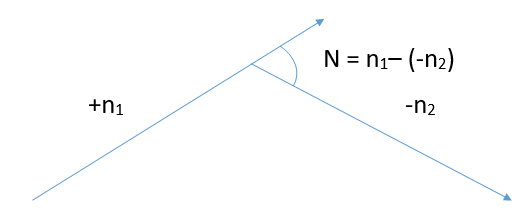
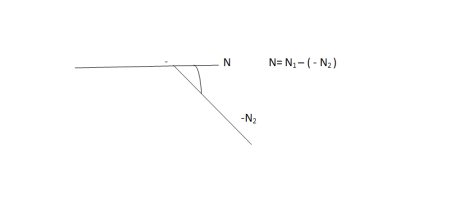
$C:\Users\Ssd\Desktop\Untitled 10.png$

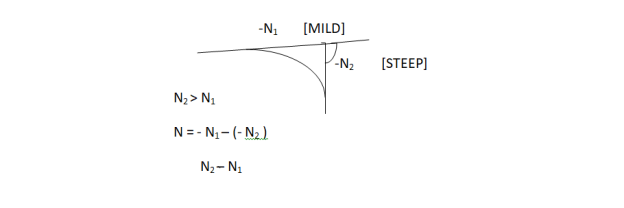
$C:\Users\Ssd\Desktop\Untitled 11.png$

Fig.12: Different Grades Curve

1. Shape of Summit Curve

Circular summit curves are ideal as the sight distance available throughout the length of the summit curve is constant.

For small deviation angles, a simple parabola is congruent with a circular curve.

Arithmetic calculations and ordinary computation are easy for a simple parabola. So, general practice is to provide simple parabola as Summit curve

2. Design Considerations

The stopping sight distance or absolute minimum sight distance should be provided on these curves and where overtaking is not prohibited, overtaking sight distance or intermediate sight distance should be provided as far as possible.

When a fast-moving vehicle travels along a summit curve, there is less discomfort to the passengers. This is because the centrifugal force will be acting upwards while the vehicle negotiates a summit curve which is against the gravity and hence a part of the tyre pressure is relieved.

P: Centrifugal Force

W: Gravitational Force

3. Length of Summit Curve (IRC Approach):

The important design aspect of the summit curve is the determination of the length of the curve (L) which is parabolic. As noted earlier, the length of the curve is guided by the sight distance consideration (S). That is, a driver should be able to stop his vehicle safely if there is an obstruction on the other side of the road.

While deciding the length of the summit curve, two situations can arise depending on the uphill and downhill gradients

When the length of the curve is greater than the sight distance (L>S)
When the length of the curve is greater than the sight distance. ((L<S)

Case 1: L>S

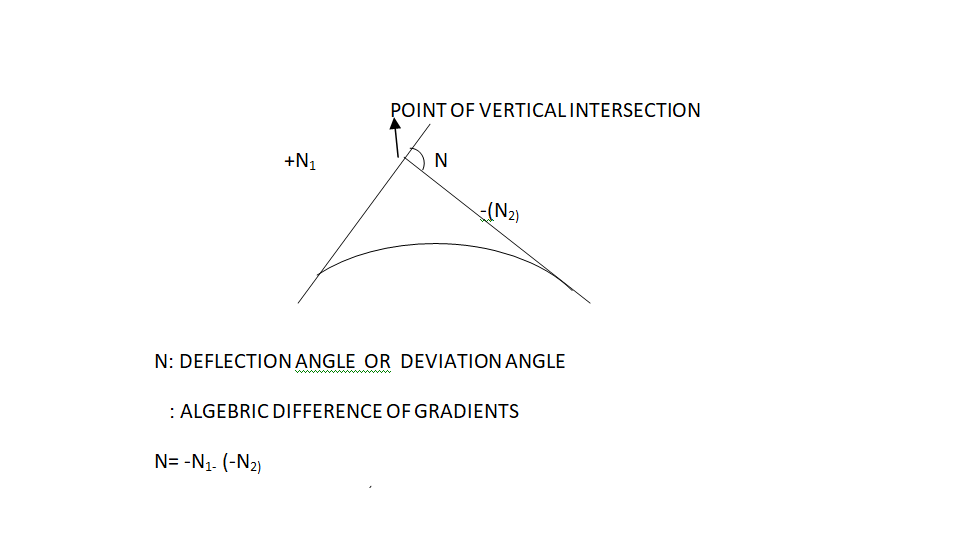
Fig.13: When L> S

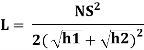
Where,

L: Length of Summit Curve

S: Sight Distance (S: SSD – when an obstruction is stationary)

(S: OSD/ISD – when an obstruction is moving)

N: Deviation Angle

h1: Drivers Eye Height = 1.2m

h2: Height of Obstruction = 0.15m

Case 2: L<S

Fig.14: When L < S

When stopping sight distance (SSD) is considered the height of the driver's eye above the road surface (h1) is taken as 1.2 meters, and the height of an object above the pavement surface (h2) is taken as 0.15 meters.

If overtaking sight distance is considered, then the value of the driver's eye height (h1) and the height of the obstruction (h2) are taken equally as 1.2 meters.

2.10.2 Valley Curve

Valley curves or sag curves are convex downwards.

If Deflection Angle N is Negative, the vertical curve is Valley Curve.

If the road surface is above the point of vertical intersection, then it is a Valley curve

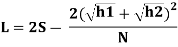
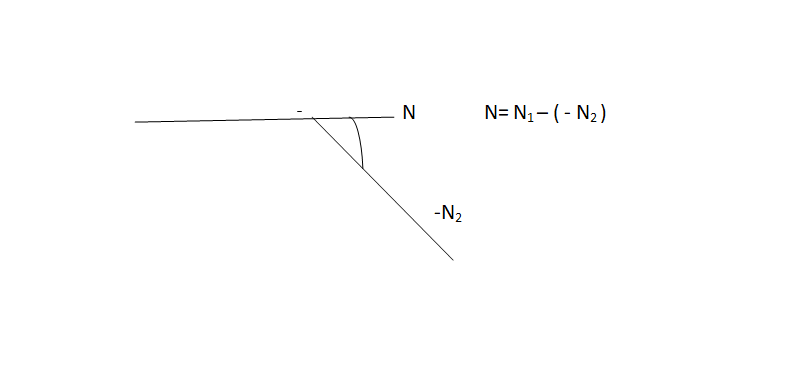
Fig.15: Valley Curve

Valley Curves are formed when two gradients meet as illustrated below:

when a descending gradient meets an ascending gradient

when a steep descending gradient meets a relatively mild descending gradient

when a descending/negative gradient meets a flat gradient

when a flat gradient meets an ascending gradient

when a mild ascending grade meets a steeper ascending gradient

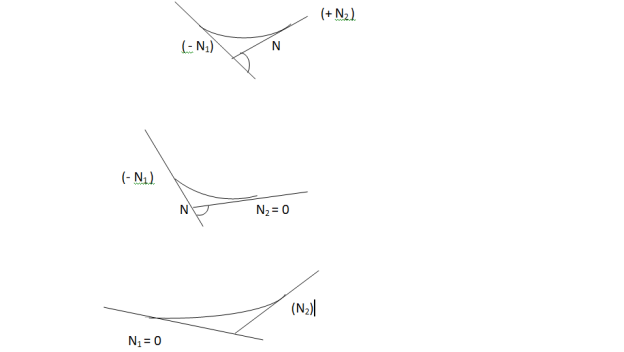
$C:\Users\Ssd\Desktop\Untitled 12.png$

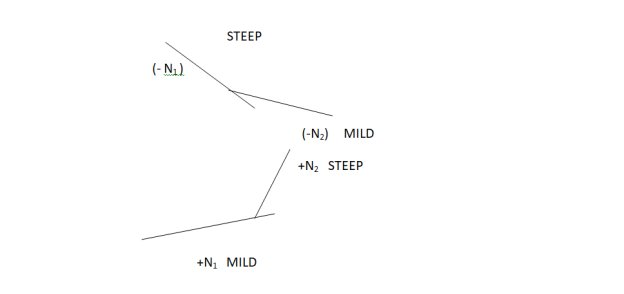
$C:\Users\Ssd\Desktop\Untitled 13.png$

Fig.16: Different Grades

2.10.3 Design Considerations

There is no restriction to sight distance at valley curves during day time. But visibility is reduced during the night. In the absence or inadequacy of street lights, the only source for visibility is with the help of headlights. Hence valley curves are designed taking into account headlight distance.

In valley curves, the centrifugal force will be acting downwards along with the weight of the vehicle, and hence impact to the vehicle will be more. This will result in jerking of the vehicle and cause discomfort to the passengers.

2.10.4 Shape of Valley Curve

For gradually introducing and increasing the centrifugal force acting downwards, the best shape that could be given for a valley curve is a transition curve.

Cubic parabola is generally preferred in vertical valley curves.

2.10.5 Length of Valley Curve (IRC Approach):

23The valley curve is made fully transitional by providing two similar transition curves of equal length. The transitional curve is set out by a cubic parabola.

The length of the Valley Transition Curve is based on two criteria

Comfort Criteria
Safety Criteria

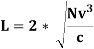
Comfort or Centrifugal Acceleration Criteria

Where,

L: Total Length of Valley Curve

N: Deviation Angle

C: Allowable rate of change of centrifugal acceleration = 0.61 m/s3

B. Safety or Headlight Sight Distance Criteria

While deciding the length of the valley curve for headlight distance, two situations can arise depending on the uphill and downhill gradients

When the length of the curve is greater than stopping sight distance (L>S)
When the length of the curve is greater than stopping sight distance. ((L<S)

Case 1: L>S

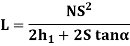
Where,

L: Total Length of Valley Curve

N: Deviation Angle

h1: Height of Headlight = 0.75m

α: Headlight beam angle = 1°

S: Headlight Sight Distance, m

Case 2: L<S

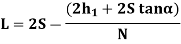
Key Takeaways:

Centrifugal Acceleration: -First, the true gravitational acceleration, of magnitude, which always points directly toward the center of the Earth. Second, the so-called centrifugal acceleration.

Line of sight: -Line-of-sight propagation is a characteristic of electromagnetic radiation or acoustic wave propagation which means waves travel in a direct path from the source to the destination.

References:

1. L.R. Kadiyali, Transportation Engineering, Khanna Publishing House

2. Saxena, Subhash C, A Textbook of Highway and Traffic Engineering, CBS Publishers &Distributors, New Delhi

3. Kumar, R Srinivasa, “A Textbook of Highway Engineering”, Universities Press,Hyderabad.

4. Kumar, R Srinivasa, “Pavement Design”, Universities Press, Hyderabad.

5. Chakraborty Partha& Das Animesh., “Principles of Transportation Engineering”,Prentice Hall (India), New Delhi,

6. IRC: 37- Latest revision, “Tentative Guidelines for the design of Flexible Pavements”Indian Roads Congress, New Delhi

7. IRC:58-2015 Guidelines for the Design of Plain Jointed Rigid Pavements for Highways(Fourth Revision) (with CD)

8. IRC:65-2017 Guidelines for Planning and Design of Roundabouts (First Revision)

9. IRC:73-1980 Geometric Design Standards for Rural (Non-Urban) Highways

10. IRC:106-1990 Guidelines for Capacity of Urban Roads in Plain Areas

11. IRC:93-1985 Guidelines on Design and Installation of Road Traffic Signals.

12. IRC:92-2017 Guidelines for Design of Interchanges in Urban Areas (First Revision)

13. IRC: SP: 68-2005, “Guidelines for Construction of Roller Compacted Concrete Pavements”,Indian Roads Congress, New Delhi.

14. IRC: 15-2002, “Standard Specifications and Code of Practice for construction of ConcreteRoads” Indian Roads Congress, New Delhi.

15. MORTH, “Specifications for Road and Bridge Works”, Ministry of Shipping, RoadTransport & Highways, Published by Indian Roads Congress, New Delhi.

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined