Module 3
Differential Calculus-II
Partial Differentiation
If 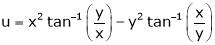
Prove that 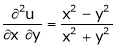
Partial differentiation of function of function
If z = f(u) and  . Then z becomes a function of x & y. In this case, z becomes a function of x & y.
. Then z becomes a function of x & y. In this case, z becomes a function of x & y.
i.e.

Then
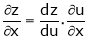 ,
,
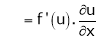
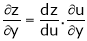
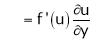
Similarly
If 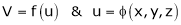
Then z becomes a function of x, y & z.
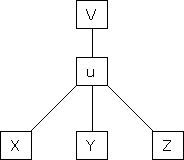
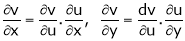
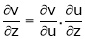 …………….
…………….
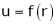
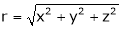
Prove that
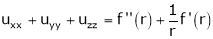
2. If V = 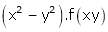 show that
show that
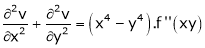
3. If 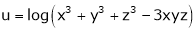 show that
show that
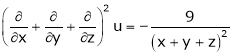
4. If 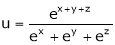 then prove that
then prove that
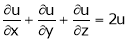
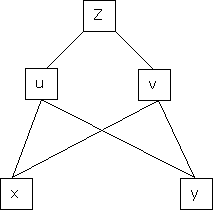
Partial Differentiation of composite function
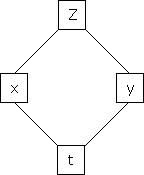
a) Let 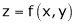 and
and 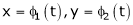 , then z becomes a function of
, then z becomes a function of  , In this case, z is called a composite function of
, In this case, z is called a composite function of  .
.
i.e.
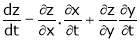
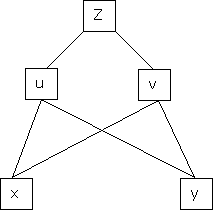
b) Let 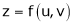 possess continuous partial derivatives and let
possess continuous partial derivatives and let 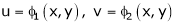 possess continuous partial derivatives, then z is called a composite function of x and y.
possess continuous partial derivatives, then z is called a composite function of x and y.
i.e.
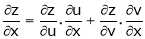
&
Continuing in this way, …..
Ex. If 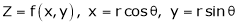 Then prove that
Then prove that
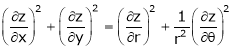
Ex. If 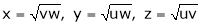 then prove that
then prove that
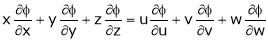
Where  is the function of x, y, z.
is the function of x, y, z.
Ex. If 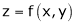 where
where 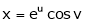 ,
,
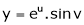 then show that,
then show that,
i) 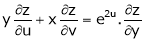
ii) 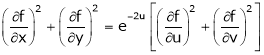
Notations of partial derivatives of the variable to be treated as a constant
Let
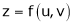 and
and 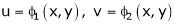
i.e.
Then 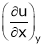 means the partial derivative of u w.r.t. x treating y const.
means the partial derivative of u w.r.t. x treating y const.
To find 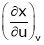 from given reactions we first express x in terms of u & v.
from given reactions we first express x in terms of u & v.
i.e.  & then diff. x w.r.t. u treating v constant.
& then diff. x w.r.t. u treating v constant.
To find 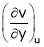 express v as a function of y and u i.e.
express v as a function of y and u i.e.  then diff. v w.r.t. y treating u as a const.
then diff. v w.r.t. y treating u as a const.
Ex. If 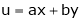 ,
, 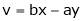 then find the value of
then find the value of
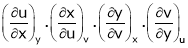 .
.
Ex. If 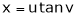 ,
, 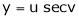 then prove that
then prove that
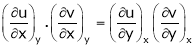
Euler’s Theorem on Homogeneous functions:
Statement:
If 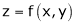 be a homogeneous function of degree n in x & y then,
be a homogeneous function of degree n in x & y then,
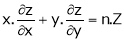
Deductions from Euler’s theorem
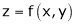
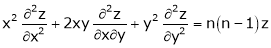 .
.
2. If  be a homogeneous function of degree n in x & y and also
be a homogeneous function of degree n in x & y and also  then,
then,
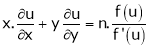
And

Where 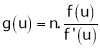
Ex.
If 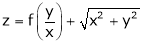 , find the value of
, find the value of
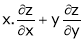
Ex.
If 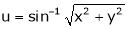 then find the value of
then find the value of 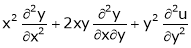
Ex. If 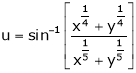 then prove
then prove
That 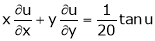
Ex. If 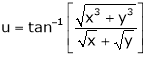 the prove that
the prove that
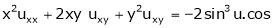
Ex. If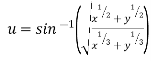 then show
then show
That 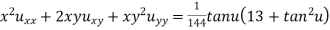
Taylor series:
The taylor’s series can be represented as the following
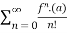 (x-a)n
(x-a)n
Example 1:
Find the taylor series for the following:
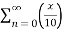
 =
= 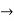
 <1
<1
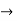 (x/10)<1 and (x/10) > -1
(x/10)<1 and (x/10) > -1
Therefore radius of convergence is (-10,10)
 ROC =10
ROC =10
Example 2:
f(n)5 = 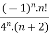
here the ROC is 4
example 2:
compute the Taylor series centerd at zero for f(x)= sinx
solution:
f(x)=sinx f(0)=0
f’(x)=cosx f’(0)=1
f’’(x)=-sinx f’’(0)=0
f’’’(x)= -cosx f’’’(0)=-1
f(4)(x)= cosx f(4) (0)= 1
applying taylor series we get
T(x) = 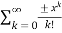 =
= 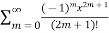 = x-
= x-
Thus turns out to converge x to sinx.
Maclaurian series:
Example 3:
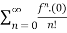 (x)n
(x)n
Example:
f(x)=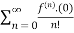
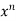
= f(0)+f’(0)x+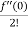 x2 +
x2 + 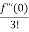 x3 +......
x3 +......
= 1+x+x2 +x3 + .....
= 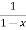

Example 4:
Find the maclurian series for f(x)= ex
Solution:
To get maclurian series,we look at the Taylor series polynomials for f near 0 and let them keep going.
Considering for example 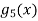

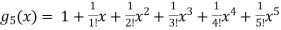
By maclurian series we get,
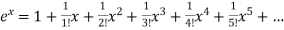 +
+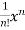
Example 1:
Find out the maxima and minima of the function

Solution:
Given 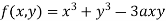 …(i)
…(i)
Partially differentiating (i) with respect to x we get
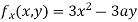 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
 ….(iii)
….(iii)
Now, form the equations 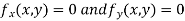
Using (ii) and (iii) we get
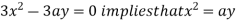
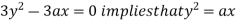
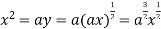 using above two equations
using above two equations
Squaring both side we get

Or 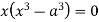
This show that 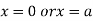
Also we get 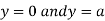
Thus we get the pair of value as 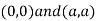
Now, we calculate
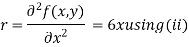
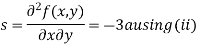
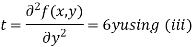
Putting above values in

At point (0,0) we get
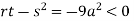
So, the point (0,0) is a saddle point.
At point  we get
we get
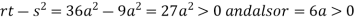
So the point 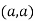 is the minimum point where
is the minimum point where 
In case 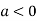
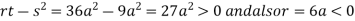
So the point 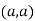 is the maximum point where
is the maximum point where 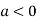
Example 2:
Find the maximum and minimum point of the function
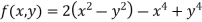
Partially differentiating given equation with respect to and x and y then equate them to zero
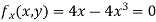

On solving above we get 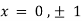
Also 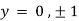
Thus we get the pair of values (0,0), (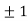 ,0) and (0,
,0) and (0,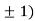
Now, we calculate
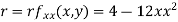
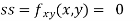
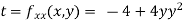
At the point (0,0)
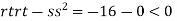
So function has saddle point at (0,0).
At the point (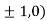
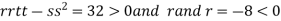
So the function has maxima at this point ( .
.
At the point (0,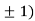

So the function has minima at this point (0,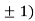 .
.
At the point (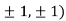
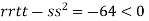
So the function has an saddle point at (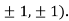
Example 3:
Find the maximum and minimum value of 
Let 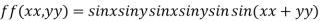
Partially differentiating given function with respect to x and y and equate it to zero
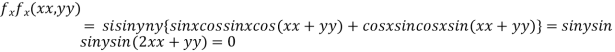 ..(i)
..(i)
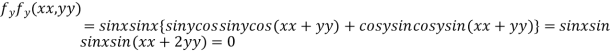 ..(ii)
..(ii)
On solving (i) and (ii) we get
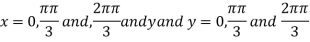
Thus pair of values are 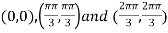
Now, we calculate
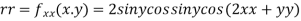
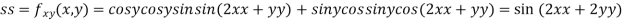
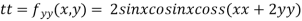
At the point (0,0)
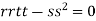
So further investigation is required
On the x axis y = 0 , f(x,0)=0
On the line y=x, 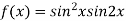
At the point 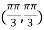

So that the given function has maximum value at 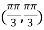
Therefore maximum value of given function
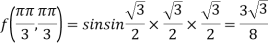
At the point 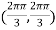
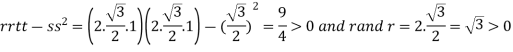
So that the given function has minimum value at 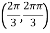
Therefore minimum value of the given function
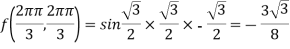
Example 1:
Determine the Jaccobian matrix of the function f: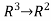 given by f(x,y,z)=(xy+2yz,2xy2z).
given by f(x,y,z)=(xy+2yz,2xy2z).
Solution:
We first f = (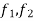 ) where
) where 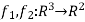 given by f(x,y,z) = xy+2yz and
given by f(x,y,z) = xy+2yz and 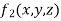 = 2x
= 2x we now compute the gradients of the following:
we now compute the gradients of the following:
 =
= 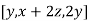
 =
= 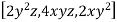
Then the Jacobian matrix is given by,
Df(x,y,z) = 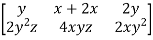
Example 2:
Determine the Jacobian matrix of the function 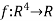 defined for all
defined for all
x= ( 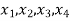 )
) 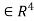 we have that,
we have that,
f(x) = f(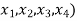
= 
= 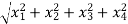
Since f is real valued function the Jacobian f is simply the gradient of f.the gradient of f is given by
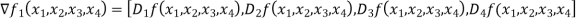
=
= 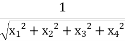 Therefore, the Jacobian f defined whenever x
Therefore, the Jacobian f defined whenever x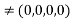
Example 3:
Suppose you are running a factor,producing some sort of widget that requires steel as a raw material.your costs are predominantly human labour,which is 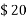 per hour for your workers,and the steel itself,which runs for $ 170 per ton.Suppose your revenue R is loosely modeled by the following equation:
per hour for your workers,and the steel itself,which runs for $ 170 per ton.Suppose your revenue R is loosely modeled by the following equation:
R(h,s) = 200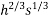
*h represents hour of labour
*s represents tons of steel,if your budget is $20,000, what is the maximum possible rvenue?
Solution:
The $ 20 per hour costs and $170 per hour ton steel costa tells us that the total cost of production in terms of h and s is,
20h+170s
Therefore the budget $20,000 can be translated to the constraint,
20h+170s
Since we need to maximize a function R(h,s), subject to a constraint,
20h+170s=20,000
The lagranges function is,
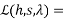 200
200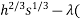 20h+170s - 20,000)
20h+170s - 20,000)
Next we set the gradient 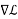 equal to zero vector.
equal to zero vector.
0 = 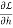
0= (200
(200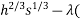 20h+170s - 20,000))
20h+170s - 20,000))
0=200.
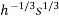 -20
-20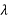
Now we derivative w.r.to s.,
0 = 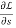
0=0=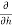 (200
(200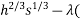 20h+170s - 20,000))
20h+170s - 20,000))
0=200.
 -170
-170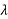
Now we set the partial derivation w.r.to., s
0 = 
0= (200
(200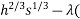 20h+170s - 20,000))
20h+170s - 20,000))
0 = -20h -170s+20,000
Putting together,the system of equations we need to solve
0 = 200 .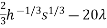
0 = 200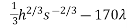
20h+170s = 20,000
Finally we get the values as,
h = 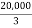 = 666.667
= 666.667
s=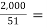 39.2157
39.2157
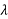 =
=  = 2.593
= 2.593
Reference Books-
1.E. Kreyszig, Advanced Engineering Mathematics, John Wiley & Sons, 2005.
2.Peter V. O’Neil, Advanced Engineering Mathematics, Thomson (Cengage) Learning, 2007.
3.Maurice D. Weir, Joel Hass, Frank R. Giordano, Thomas, Calculus, Eleventh Edition, Pearson.
4.D. Poole, Linear Algebra: A Modern Introduction, 2nd Edition, Brooks/Cole, 2005.
5.Veerarajan T., Engineering Mathematics for the first year, Tata McGraw-Hill, New Delhi, 2008.
6.Ray Wylie C and Louis C Barret, Advanced Engineering Mathematics, Tata Mc-Graw-Hill, Sixth Edition.
7.P. Sivaramakrishna Das and C. Vijayakumari, Engineering Mathematics, 1st Edition, Pearson India Education Services Pvt. Ltd
8. Advanced Engineering Mathematics. Chandrika Prasad, Reena Garg, 2018.
9. Engineering Mathematics – I. Reena Garg, 2018.