Unit - 2

Introduction to Search

2.1 Searching for solutions

Search algorithms are one of the most important areas of Artificial Intelligence. 

Problem-solving agents:

In Artificial Intelligence, Search techniques are universal problem-solving methods. Rational agents or Problem-solving agents in AI mostly used these search strategies or algorithms to solve a specific problem and provide the best result. Problem-solving agents are the goal-based agents and use atomic representation. In this topic, we will learn various problem-solving search algorithms.

Search Algorithm Terminologies:

• Search: Searching is a step by step procedure to solve a search-problem in a given search space. A search problem can have three main factors:
  1. Search Space: Search space represents a set of possible solutions, which a system may have.
  2. Start State: It is a state from where agent begins the search.
  3. Goal test: It is a function which observe the current state and returns whether the goal state is achieved or not.

• Search tree: A tree representation of search problem is called Search tree. The root of the search tree is the root node which is corresponding to the initial state.
• Actions: It gives the description of all the available actions to the agent.
• Transition model: A description of what each action do, can be represented as a transition model.
• Path Cost: It is a function which assigns a numeric cost to each path.
• Solution: It is an action sequence which leads from the start node to the goal node.
• Optimal Solution: If a solution has the lowest cost among all solutions.

Properties of Search Algorithms:

Following are the four essential properties of search algorithms to compare the efficiency of these algorithms:

Completeness: A search algorithm is said to be complete if it guarantees to return a solution if at least any solution exists for any random input.

Optimality: If a solution found for an algorithm is guaranteed to be the best solution (lowest path cost) among all other solutions, then such a solution for is said to be an optimal solution.

Time Complexity: Time complexity is a measure of time for an algorithm to complete its task.

Space Complexity: It is the maximum storage space required at any point during the search, as the complexity of the problem.

Types of search algorithms

Based on the search problems we can classify the search algorithms into uninformed (Blind search) search and informed search (Heuristic search) algorithms.

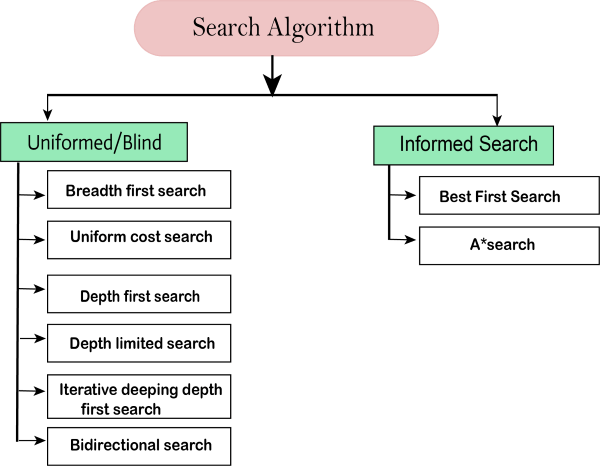
Uninformed/Blind Search:

The uninformed search does not contain any domain knowledge such as closeness, the location of the goal. It operates in a brute-force way as it only includes information about how to traverse the tree and how to identify leaf and goal nodes. Uninformed search applies a way in which search tree is searched without any information about the search space like initial state operators and test for the goal, so it is also called blind search. It examines each node of the tree until it achieves the goal node.

It can be divided into five main types:

• Breadth-first search
• Uniform cost search
• Depth-first search
• Iterative deepening depth-first search
• Bidirectional Search

Informed Search

Informed search algorithms use domain knowledge. In an informed search, problem information is available which can guide the search. Informed search strategies can find a solution more efficiently than an uninformed search strategy. Informed search is also called a Heuristic search.

Informed search can solve much complex problem which could not be solved in another way.

2.2 Uniformed search strategies

Uninformed/Blind Search:

The uninformed search does not contain any domain knowledge such as closeness, the location of the goal. It operates in a brute-force way as it only includes information about how to traverse the tree and how to identify leaf and goal nodes. Uninformed search applies a way in which search tree is searched without any information about the search space like initial state operators and test for the goal, so it is also called blind search. It examines each node of the tree until it achieves the goal node.

It can be divided into five main types:

• Breadth-first search
• Uniform cost search
• Depth-first search
• Iterative deepening depth-first search
• Bidirectional Search

Informed Search

Informed search algorithms use domain knowledge. In an informed search, problem information is available which can guide the search. Informed search strategies can find a solution more efficiently than an uninformed search strategy. Informed search is also called a Heuristic search.

A heuristic is a way which might not always be guaranteed for best solutions but guaranteed to find a good solution in reasonable time.

Informed search can solve much complex problem which could not be solved in another way.

An example of informed search algorithms is a traveling salesman problem.

1. Greedy Search
2. A* Search

Uninformed Search Algorithms

Uninformed search is a class of general-purpose search algorithms which operates in brute force-way. Uninformed search algorithms do not have additional information about state or search space other than how to traverse the tree, so it is also called blind search.

Following are the various types of uninformed search algorithms:

Breadth-first Search

Depth-first Search

Depth-limited Search

Iterative deepening depth-first search

Uniform cost search

Bidirectional Search

1. Breadth-first Search:

• Breadth-first search is the most common search strategy for traversing a tree or graph. This algorithm searches breadthwise in a tree or graph, so it is called breadth-first search.
• BFS algorithm starts searching from the root node of the tree and expands all successor node at the current level before moving to nodes of next level.
• The breadth-first search algorithm is an example of a general-graph search algorithm.
• Breadth-first search implemented using FIFO queue data structure.

Advantages:

• BFS will provide a solution if any solution exists.
• If there are more than one solutions for a given problem, then BFS will provide the minimal solution which requires the least number of steps.

Disadvantages:

• It requires lots of memory since each level of the tree must be saved into memory to expand the next level.
• BFS needs lots of time if the solution is far away from the root node.

Example:

In the below tree structure, we have shown the traversing of the tree using BFS algorithm from the root node S to goal node K. BFS search algorithm traverse in layers, so it will follow the path which is shown by the dotted arrow, and the traversed path will be:

1. S---> A--->B---->C--->D---->G--->H--->E---->F---->I---->K  

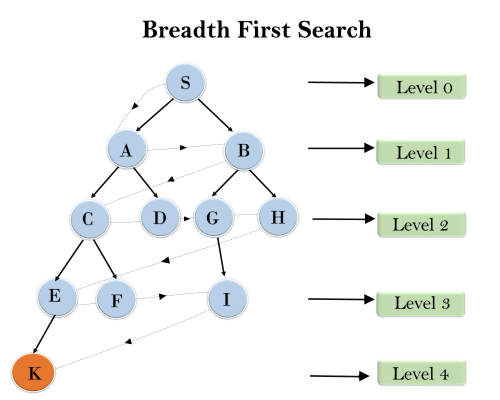
Time Complexity: Time Complexity of BFS algorithm can be obtained by the number of nodes traversed in BFS until the shallowest Node. Where the d= depth of shallowest solution and b is a node at every state.

T (b) = 1+b2+b3+.......+ bd= O (bd)

Space Complexity: Space complexity of BFS algorithm is given by the Memory size of frontier which is O(bd).

Completeness: BFS is complete, which means if the shallowest goal node is at some finite depth, then BFS will find a solution.

Optimality: BFS is optimal if path cost is a non-decreasing function of the depth of the node.

2. Depth-first Search

• Depth-first search isa recursive algorithm for traversing a tree or graph data structure.
• It is called the depth-first search because it starts from the root node and follows each path to its greatest depth node before moving to the next path.
• DFS uses a stack data structure for its implementation.
• The process of the DFS algorithm is similar to the BFS algorithm.

Note: Backtracking is an algorithm technique for finding all possible solutions using recursion.

Advantage:

• DFS requires very less memory as it only needs to store a stack of the nodes on the path from root node to the current node.
• It takes less time to reach to the goal node than BFS algorithm (if it traverses in the right path).

Disadvantage:

• There is the possibility that many states keep re-occurring, and there is no guarantee of finding the solution.
• DFS algorithm goes for deep down searching and sometime it may go to the infinite loop.

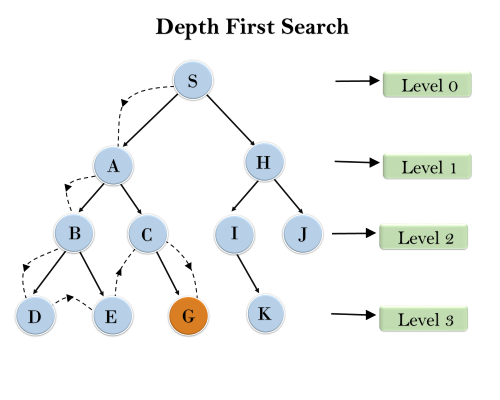
Example:

In the below search tree, we have shown the flow of depth-first search, and it will follow the order as:

Root node--->Left node ----> right node.

It will start searching from root node S, and traverse A, then B, then D and E, after traversing E, it will backtrack the tree as E has no other successor and still goal node is not found. After backtracking it will traverse node C and then G, and here it will terminate as it found goal node.

Completeness: DFS search algorithm is complete within finite state space as it will expand every node within a limited search tree.

Time Complexity: Time complexity of DFS will be equivalent to the node traversed by the algorithm. It is given by:

T(n)= 1+ n2+ n3 +.........+ nm=O(nm)

Where, m= maximum depth of any node and this can be much larger than d (Shallowest solution depth)

Space Complexity: DFS algorithm needs to store only single path from the root node, hence space complexity of DFS is equivalent to the size of the fringe set, which is O(bm).

Optimal: DFS search algorithm is non-optimal, as it may generate a large number of steps or high cost to reach to the goal node.

3. Depth-Limited Search Algorithm:

A depth-limited search algorithm is similar to depth-first search with a predetermined limit. Depth-limited search can solve the drawback of the infinite path in the Depth-first search. In this algorithm, the node at the depth limit will treat as it has no successor nodes further.

Depth-limited search can be terminated with two Conditions of failure:

• Standard failure value: It indicates that problem does not have any solution.
• Cutoff failure value: It defines no solution for the problem within a given depth limit.

Advantages:

Depth-limited search is Memory efficient.

Disadvantages:

• Depth-limited search also has a disadvantage of incompleteness.
• It may not be optimal if the problem has more than one solution.

Example:

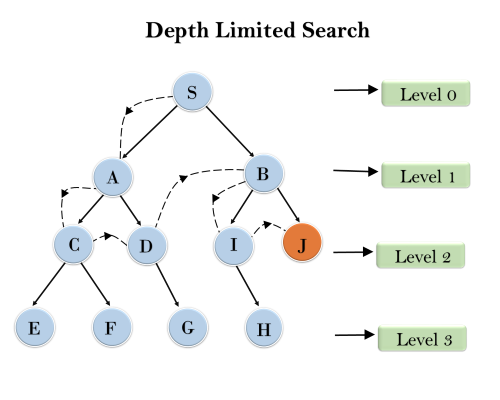
Completeness: DLS search algorithm is complete if the solution is above the depth-limit.

Time Complexity: Time complexity of DLS algorithm is O(bℓ).

Space Complexity: Space complexity of DLS algorithm is O(b×ℓ).

Optimal: Depth-limited search can be viewed as a special case of DFS, and it is also not optimal even if ℓ>d.

4. Uniform-cost Search Algorithm:

Uniform-cost search is a searching algorithm used for traversing a weighted tree or graph. This algorithm comes into play when a different cost is available for each edge. The primary goal of the uniform-cost search is to find a path to the goal node which has the lowest cumulative cost. Uniform-cost search expands nodes according to their path costs form the root node. It can be used to solve any graph/tree where the optimal cost is in demand. A uniform-cost search algorithm is implemented by the priority queue. It gives maximum priority to the lowest cumulative cost. Uniform cost search is equivalent to BFS algorithm if the path cost of all edges is the same.

Advantages:

• Uniform cost search is optimal because at every state the path with the least cost is chosen.

Disadvantages:

• It does not care about the number of steps involve in searching and only concerned about path cost. Due to which this algorithm may be stuck in an infinite loop.

Example:

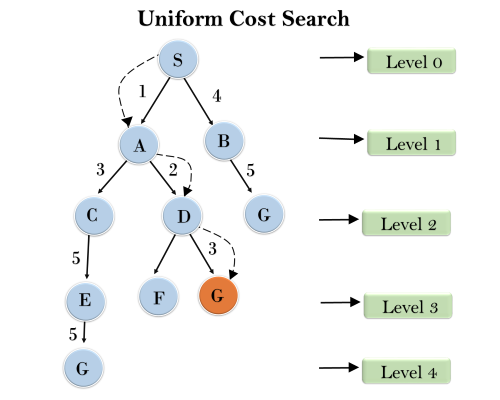
Completeness:

Uniform-cost search is complete, such as if there is a solution, UCS will find it.

Time Complexity:

Let C* is Cost of the optimal solution, and ε is each step to get closer to the goal node. Then the number of steps is = C*/ε+1. Here we have taken +1, as we start from state 0 and end to C*/ε.

Hence, the worst-case time complexity of Uniform-cost search isO(b1 + [C*/ε])/.

Space Complexity:

The same logic is for space complexity so, the worst-case space complexity of Uniform-cost search is O(b1 + [C*/ε]).

Optimal:

Uniform-cost search is always optimal as it only selects a path with the lowest path cost.

5. Iterative deepening depth-first Search:

The iterative deepening algorithm is a combination of DFS and BFS algorithms. This search algorithm finds out the best depth limit and does it by gradually increasing the limit until a goal is found.

This algorithm performs depth-first search up to a certain "depth limit", and it keeps increasing the depth limit after each iteration until the goal node is found.

This Search algorithm combines the benefits of Breadth-first search's fast search and depth-first search's memory efficiency.

The iterative search algorithm is useful uninformed search when search space is large, and depth of goal node is unknown.

Advantages:

• It combines the benefits of BFS and DFS search algorithm in terms of fast search and memory efficiency.

Disadvantages:

• The main drawback of IDDFS is that it repeats all the work of the previous phase.

Example:

Following tree structure is showing the iterative deepening depth-first search. IDDFS algorithm performs various iterations until it does not find the goal node. The iteration performed by the algorithm is given as:

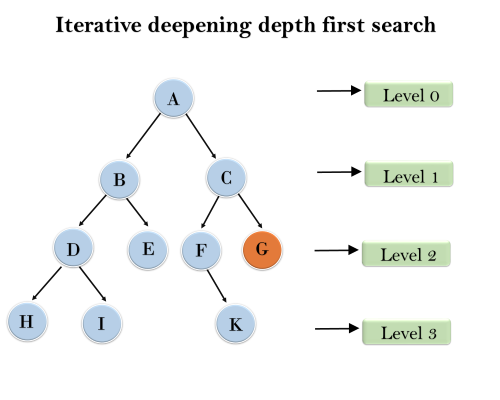
1'st Iteration-----> A
2'nd Iteration----> A, B, C
3'rd Iteration------>A, B, D, E, C, F, G
4'th Iteration------>A, B, D, H, I, E, C, F, K, G
In the fourth iteration, the algorithm will find the goal node.

Completeness:

This algorithm is complete is ifthe branching factor is finite.

Time Complexity:

Let's suppose b is the branching factor and depth is d then the worst-case time complexity is O(bd).

Space Complexity:

The space complexity of IDDFS will be O(bd).

Optimal:

IDDFS algorithm is optimal if path cost is a non- decreasing function of the depth of the node.

6. Bidirectional Search Algorithm:

Bidirectional search algorithm runs two simultaneous searches, one form initial state called as forward-search and other from goal node called as backward-search, to find the goal node. Bidirectional search replaces one single search graph with two small subgraphs in which one starts the search from an initial vertex and other starts from goal vertex. The search stops when these two graphs intersect each other.

Bidirectional search can use search techniques such as BFS, DFS, DLS, etc.

Advantages:

• Bidirectional search is fast.
• Bidirectional search requires less memory

Disadvantages:

• Implementation of the bidirectional search tree is difficult.

In bidirectional search, one should know the goal state in advance.

Example:

In the below search tree, bidirectional search algorithm is applied. This algorithm divides one graph/tree into two sub-graphs. It starts traversing from node 1 in the forward direction and starts from goal node 16 in the backward direction.

The algorithm terminates at node 9 where two searches meet.

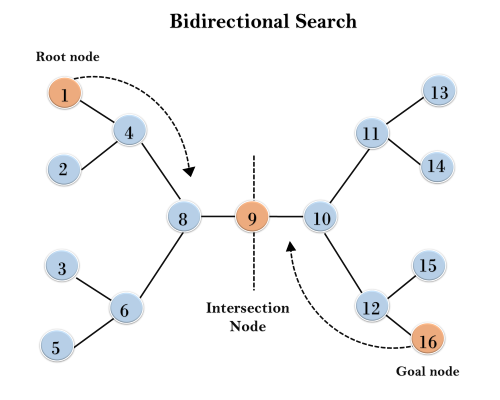
Completeness: Bidirectional Search is complete if we use BFS in both searches.

Time Complexity: Time complexity of bidirectional search using BFS is O(bd).

Space Complexity: Space complexity of bidirectional search is O(bd).

Optimal: Bidirectional search is Optimal.

2.3 Informed search strategies

Heuristics function: Heuristic is a function which is used in Informed Search, and it finds the most promising path. It takes the current state of the agent as its input and produces the estimation of how close agent is from the goal. The heuristic method, however, might not always give the best solution, but it guaranteed to find a good solution in reasonable time. Heuristic function estimates how close a state is to the goal. It is represented by h(n), and it calculates the cost of an optimal path between the pair of states. The value of the heuristic function is always positive.

Admissibility of the heuristic function is given as:

1. h(n) <= h*(n)  

Here h(n) is heuristic cost, and h*(n) is the estimated cost. Hence heuristic cost should be less than or equal to the estimated cost.

Pure Heuristic Search:

Pure heuristic search is the simplest form of heuristic search algorithms. It expands nodes based on their heuristic value h(n). It maintains two lists, OPEN and CLOSED list. In the CLOSED list, it places those nodes which have already expanded and in the OPEN list, it places nodes which have yet not been expanded.

On each iteration, each node n with the lowest heuristic value is expanded and generates all its successors and n is placed to the closed list. The algorithm continues unit a goal state is found.

In the informed search we will discuss two main algorithms which are given below:

• Best First Search Algorithm(Greedy search)
• A* Search Algorithm

Best-first Search Algorithm (Greedy Search):

Greedy best-first search algorithm always selects the path which appears best at that moment. It is the combination of depth-first search and breadth-first search algorithms. It uses the heuristic function and search. Best-first search allows us to take the advantages of both algorithms. With the help of best-first search, at each step, we can choose the most promising node. In the best first search algorithm, we expand the node which is closest to the goal node and the closest cost is estimated by heuristic function, i.e.

1. f(n)= g(n).   

Were, h(n)= estimated cost from node n to the goal.

The greedy best first algorithm is implemented by the priority queue.

Best first search algorithm:

• Step 1: Place the starting node into the OPEN list.
• Step 2: If the OPEN list is empty, Stop and return failure.
• Step 3: Remove the node n, from the OPEN list which has the lowest value of h(n), and places it in the CLOSED list.
• Step 4: Expand the node n, and generate the successors of node n.
• Step 5: Check each successor of node n, and find whether any node is a goal node or not. If any successor node is goal node, then return success and terminate the search, else proceed to Step 6.
• Step 6: For each successor node, algorithm checks for evaluation function f(n), and then check if the node has been in either OPEN or CLOSED list. If the node has not been in both lists, then add it to the OPEN list.
• Step 7: Return to Step 2.

Advantages:

• Best first search can switch between BFS and DFS by gaining the advantages of both the algorithms.
• This algorithm is more efficient than BFS and DFS algorithms.

Disadvantages:

• It can behave as an unguided depth-first search in the worst case scenario.
• It can get stuck in a loop as DFS.
• This algorithm is not optimal.

Example:

Consider the below search problem, and we will traverse it using greedy best-first search. At each iteration, each node is expanded using evaluation function f(n)=h(n), which is given in the below table.

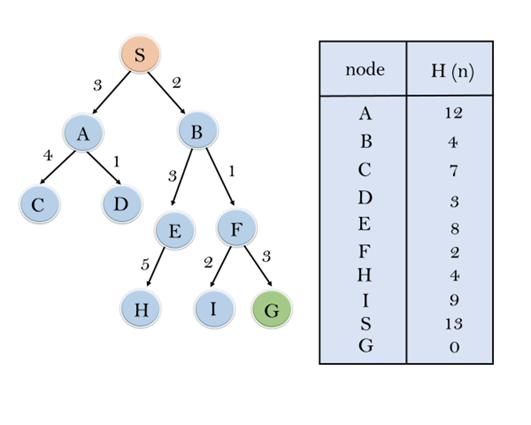
In this search example, we are using two lists which are OPEN and CLOSED Lists. Following are the iteration for traversing the above example.

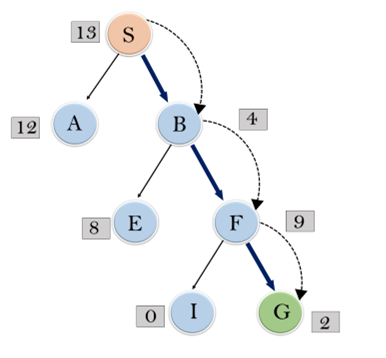
Expand the nodes of S and put in the CLOSED list

Initialization: Open [A, B], Closed [S]

Iteration 1: Open [A], Closed [S, B]

Iteration 2: Open [E, F, A], Closed [S, B]: Open [E, A], Closed [S, B, F]

Iteration 3: Open [I, G, E, A], Closed [S, B, F]: Open [I, E, A], Closed [S, B, F, G]

Hence the final solution path will be: S----> B----->F----> G

Time Complexity: The worst case time complexity of Greedy best first search is O(bm).

Space Complexity: The worst case space complexity of Greedy best first search is O(bm). Where, m is the maximum depth of the search space.

Complete: Greedy best-first search is also incomplete, even if the given state space is finite.

Optimal: Greedy best first search algorithm is not optimal.

A* Search Algorithm

A* search is the most commonly known form of best-first search. It uses heuristic function h(n), and cost to reach the node n from the start state g(n). It has combined features of UCS and greedy best-first search, by which it solve the problem efficiently. A* search algorithm finds the shortest path through the search space using the heuristic function. This search algorithm expands less search tree and provides optimal result faster. A* algorithm is similar to UCS except that it uses g(n)+h(n) instead of g(n).

In A* search algorithm, we use search heuristic as well as the cost to reach the node. Hence we can combine both costs as following, and this sum is called as a fitness number.

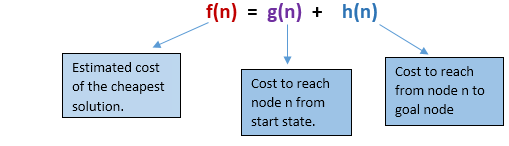
At each point in the search space, only those node is expanded which have the lowest value of f(n), and the algorithm terminates when the goal node is found.

Algorithm of A* search:

Step1: Place the starting node in the OPEN list.

Step 2: Check if the OPEN list is empty or not, if the list is empty then return failure and stops.

Step 3: Select the node from the OPEN list which has the smallest value of evaluation function (g+h), if node n is goal node, then return success and stop, otherwise

Step 4: Expand node n and generate all of its successors, and put n into the closed list. For each successor n', check whether n' is already in the OPEN or CLOSED list, if not then compute evaluation function for n' and place into Open list.

Step 5: Else if node n' is already in OPEN and CLOSED, then it should be attached to the back pointer which reflects the lowest g(n') value.

Step 6: Return to Step 2.

Advantages:

• A* search algorithm is the best algorithm than other search algorithms.
• A* search algorithm is optimal and complete.
• This algorithm can solve very complex problems.

Disadvantages:

• It does not always produce the shortest path as it mostly based on heuristics and approximation.
• A* search algorithm has some complexity issues.
• The main drawback of A* is memory requirement as it keeps all generated nodes in the memory, so it is not practical for various large-scale problems.

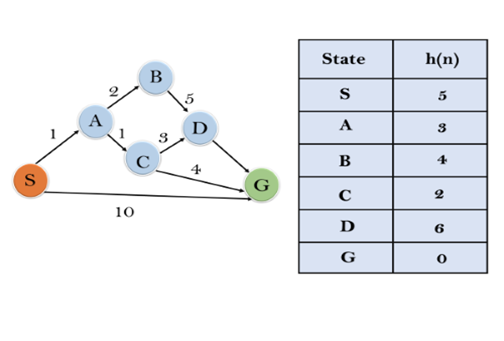
Example:

In this example, we will traverse the given graph using the A* algorithm. The heuristic value of all states is given in the below table so we will calculate the f(n) of each state using the formula f(n)= g(n) + h(n), where g(n) is the cost to reach any node from start state.

Here we will use OPEN and CLOSED list.

Solution:

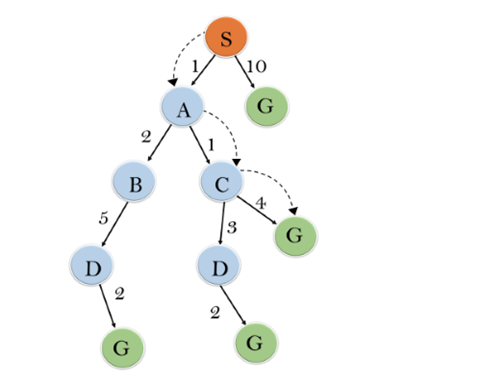
Initialization: {(S, 5)}

Iteration1: {(S--> A, 4), (S-->G, 10)}

Iteration2: {(S--> A-->C, 4), (S--> A-->B, 7), (S-->G, 10)}

Iteration3: {(S--> A-->C--->G, 6), (S--> A-->C--->D, 11), (S--> A-->B, 7), (S-->G, 10)}

Iteration 4 will give the final result, as S--->A--->C--->G it provides the optimal path with cost 6.

Points to remember:

• A* algorithm returns the path which occurred first, and it does not search for all remaining paths.
• The efficiency of A* algorithm depends on the quality of heuristic.
• A* algorithm expands all nodes which satisfy the condition f(n) <="" li="">

Complete: A* algorithm is complete as long as:

• Branching factor is finite.
• Cost at every action is fixed.

Optimal: A* search algorithm is optimal if it follows below two conditions:

• Admissible: the first condition requires for optimality is that h(n) should be an admissible heuristic for A* tree search. An admissible heuristic is optimistic in nature.
• Consistency: Second required condition is consistency for only A* graph-search.

If the heuristic function is admissible, then A* tree search will always find the least cost path.

Time Complexity: The time complexity of A* search algorithm depends on heuristic function, and the number of nodes expanded is exponential to the depth of solution d. So the time complexity is O(b^d), where b is the branching factor.

Space Complexity: The space complexity of A* search algorithm is O(b^d)

2.4 Local search algorithms and optimistic problems

A local search algorithm completes its task by traversing on a single current node rather than multiple paths and following the neighbours of that node generally.

Although local search algorithms are not systematic, still they have the following two advantages:

• Local search algorithms use a very little or constant amount of memory as they operate only on a single path.
• Most often, they find a reasonable solution in large or infinite state spaces where the classical or systematic algorithms do not work.

Working of a Local search algorithm

Consider the below state-space landscape having both:

• Location: It is defined by the state.
• Elevation: It is defined by the value of the objective function or heuristic cost function.

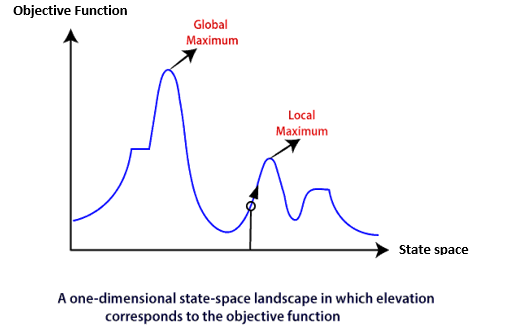
The local search algorithm explores the above landscape by finding the following two points:

• Global Minimum: If the elevation corresponds to the cost, then the task is to find the lowest valley, which is known as Global Minimum.   
• Global Maxima: If the elevation corresponds to an objective function, then it finds the highest peak which is called as Global Maxima. It is the highest point in the valley.

Some different types of local searches:

• Hill-climbing Search
• Simulated Annealing
• Local Beam Search

Note: Local search algorithms do not burden to remember all the nodes in the memory; it operates on complete state-formulation.

Hill Climbing Algorithm:

Hill climbing search is a local search problem. The purpose of the hill climbing search is to climb a hill and reach the topmost peak/ point of that hill. It is based on the heuristic search technique where the person who is climbing up on the hill estimates the direction which will lead him to the highest peak.                                              

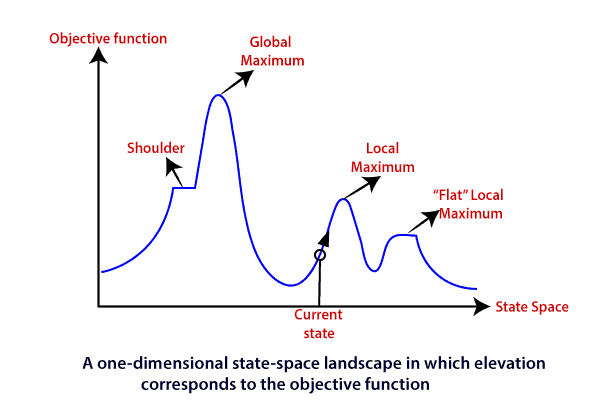
State-space Landscape of Hill climbing algorithm

To understand the concept of hill climbing algorithm, consider the below landscape representing the goal state/peak and the current state of the climber. The topographical regions shown in the figure can be defined as:

• Global Maximum: It is the highest point on the hill, which is the goal state.
• Local Maximum: It is the peak higher than all other peaks but lower than the global maximum.
• Flat local maximum: It is the flat area over the hill where it has no uphill or downhill. It is a saturated point of the hill.
• Shoulder: It is also a flat area where the summit is possible.
• Current state: It is the current position of the person.

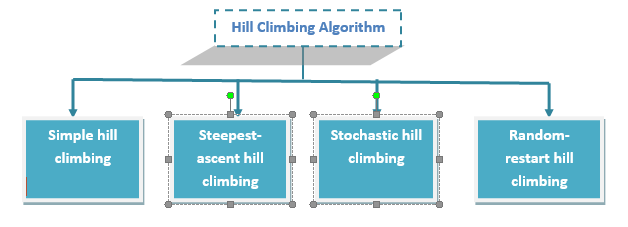
Types of Hill climbing search algorithm

There are following types of hill-climbing search:

• Simple hill climbing
• Steepest-ascent hill climbing
• Stochastic hill climbing
• Random-restart hill climbing

Simple hill climbing search

Simple hill climbing is the simplest technique to climb a hill. The task is to reach the highest peak of the mountain. Here, the movement of the climber depends on his move/steps. If he finds his next step better than the previous one, he continues to move else remain in the same state. This search focus only on his previous and next step.

Simple hill climbing Algorithm

1. Create a CURRENT node, NEIGHBOUR node, and a GOAL node.
2. If the CURRENT node=GOAL node, return GOAL and terminate the search.
3. Else CURRENT node<= NEIGHBOUR node, move ahead.
4. Loop until the goal is not reached or a point is not found.

Steepest-ascent hill climbing

Steepest-ascent hill climbing is different from simple hill climbing search. Unlike simple hill climbing search, It considers all the successive nodes, compares them, and choose the node which is closest to the solution. Steepest hill climbing search is similar to best-first search because it focuses on each node instead of one.

Note: Both simple, as well as steepest-ascent hill climbing search, fails when there is no closer node.

Steepest-ascent hill climbing algorithm

1. Create a CURRENT node and a GOAL node.
2. If the CURRENT node=GOAL node, return GOAL and terminate the search.
3. Loop until a better node is not found to reach the solution.
4. If there is any better successor node present, expand it.
5. When the GOAL is attained, return GOAL and terminate.

Stochastic hill climbing

Stochastic hill climbing does not focus on all the nodes. It selects one node at random and decides whether it should be expanded or search for a better one.

Random-restart hill climbing

Random-restart algorithm is  based on try and try strategy. It iteratively searches the node and selects the best one at each step until the goal is not found. The success depends most commonly on the shape of the hill. If there are few plateaus, local maxima, and ridges, it becomes easy to reach the destination.

Limitations of Hill climbing algorithm

Hill climbing algorithm is a fast and furious approach. It finds the solution state rapidly because it is quite easy to improve a bad state. But, there are following limitations of this search:

• Local Maxima: It is that peak of the mountain which is highest than all its neighbouring states but lower than the global maxima. It is not the goal peak because there is another peak higher than it.

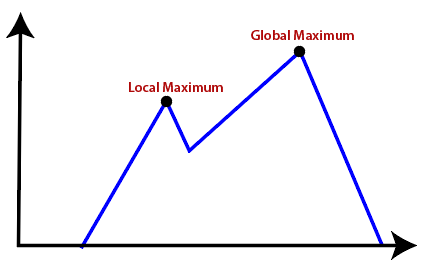
• Plateau: It is a flat surface area where no uphill exists. It becomes difficult for the climber to decide that in which direction he should move to reach the goal point. Sometimes, the person gets lost in the flat area.

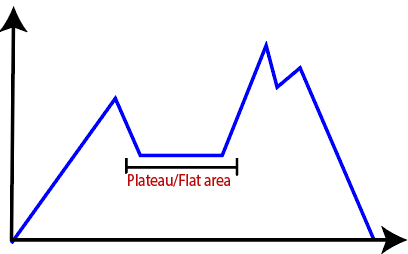
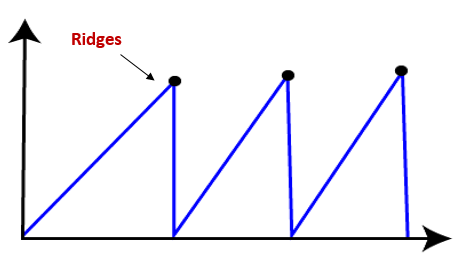
• Ridges: It is a challenging problem where the person finds two or more local maxima of the same height commonly. It becomes difficult for the person to navigate the right point and stuck to that point itself.

Simulated Annealing

Simulated annealing is similar to the hill climbing algorithm.  It works on the current situation. It picks a random move instead of picking the best move. If the move leads to the improvement of the current situation, it is always accepted as a step towards the solution state, else it accepts the move having a probability less than 1.

This search technique was first used in 1980 to solve VLSI layout problems. It is also applied for factory scheduling and other large optimization tasks.

Local Beam Search

Local beam search is quite different from random-restart search. It keeps track of k states instead of just one. It selects k randomly generated states, and expand them at each step. If any state is a goal state, the search stops with success. Else it selects the best k successors from the complete list and repeats the same process.

In random-restart search where each search process runs independently, but in local beam search, the necessary information is shared between the parallel search processes.

Disadvantages of Local Beam search

• This search can suffer from a lack of diversity among the k states.
• It is an expensive version of hill climbing search.

2.5 Adversarial Search

Adversarial search is a game-playing technique where the agents are surrounded by a competitive environment. A conflicting goal is given to the agents (multiagent).

These agents compete with one another and try to defeat one another in order to win the game.

Such conflicting goals give rise to the adversarial search. Here, game-playing means discussing those games where human intelligence and logic factor is used, excluding other factors such as luck factor. Tic-tac-toe, chess, checkers, etc., are such type of games where no luck factor works, only mind works.

Mathematically, this search is based on the concept of ‘Game Theory.’ According to game theory, a game is played between two players. To complete the game, one has to win the game and the other looses automatically.’

Techniques required to get the best optimal solution

There is always a need to choose those algorithms which provide the best optimal solution in a limited time. So, we use the following techniques which could fulfill our requirements:

• Pruning: A technique which allows ignoring the unwanted portions of a search tree which make no difference in its final result.
• Heuristic Evaluation Function: It allows to approximate the cost value at each level of the search tree, before reaching the goal node.

Elements of Game Playing search

To play a game, we use a game tree to know all the possible choices and to pick the best one out. There are following elements of a game-playing:

• S0: It is the initial state from where a game begins.
• PLAYER (s): It defines which player is having the current turn to make a move in the state.
• ACTIONS (s): It defines the set of legal moves to be used in a state.
• RESULT (s, a): It is a transition model which defines the result of a move.
• TERMINAL-TEST (s): It defines that the game has ended and returns true.
• UTILITY (s,p): It defines the final value with which the game has ended. This function is also known as Objective function or Payoff function. The price which the winner will get i.e.
• (-1): If the PLAYER loses.
• (+1): If the PLAYER wins.
• (0): If there is a draw between the PLAYERS.

For example, in chess, tic-tac-toe, we have two or three possible outcomes. Either to win, to lose, or to draw the match with values +1, -1 or 0.

Let’s understand the working of the elements with the help of a game tree designed for tic-tac-toe. Here, the node represents the game state and edges represent the moves taken by the players.

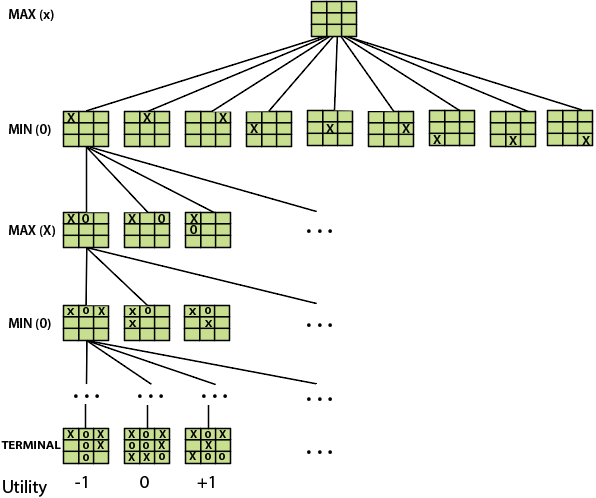
A game-tree for tic-tac-toe

• INITIAL STATE (S0): The top node in the game-tree represents the initial state in the tree and shows all the possible choice to pick out one.
• PLAYER (s): There are two players, MAX and MIN. MAX begins the game by picking one best move and place X in the empty square box.  
• ACTIONS (s): Both the players can make moves in the empty boxes chance by chance.
• RESULT (s, a): The moves made by MIN and MAX will decide the outcome of the game.
• TERMINAL-TEST(s): When all the empty boxes will be filled, it will be the terminating state of the game.
• UTILITY: At the end, we will get to know who wins: MAX or MIN, and accordingly, the price will be given to them.

Types of algorithms in Adversarial search

In a normal search, we follow a sequence of actions to reach the goal or to finish the game optimally. But in an adversarial search, the result depends on the players which will decide the result of the game. It is also obvious that the solution for the goal state will be an optimal solution because the player will try to win the game with the shortest path and under limited time.

There are following types of adversarial search:

• Minmax Algorithm
• Alpha-beta Pruning

Minimax Strategy

In artificial intelligence, minimax is a decision-making strategy under game theory, which is used to minimize the losing chances in a game and to maximize the winning chances. This strategy is also known as ‘Minmax,’ ’MM,’ or ‘Saddle point.’ Basically, it is a two-player game strategy where if one wins, the other loose the game. This strategy simulates those games that we play in our day-to-day life. Like, if two persons are playing chess, the result will be in favour of one player and will unfavoured the other one. The person who will make his best try, efforts as well as cleverness, will surely win.

We can easily understand this strategy via game tree– where the nodes represent the states of the game and edges represent the moves made by the players in the game.

Players will be two namely:

• MIN: Decrease the chances of MAX to win the game.
• MAX: Increases his chances of winning the game.

They both play the game alternatively, i.e., turn by turn and following the above strategy, i.e., if one wins, the other will definitely lose it. Both players look at one another as competitors and will try to defeat one-another, giving their best.

In minimax strategy, the result of the game or the utility value is generated by a heuristic function by propagating from the initial node to the root node. It follows the backtracking technique and backtracks to find the best choice. MAX will choose that path which will increase its utility value and MIN will choose the opposite path which could help it to minimize MAX’s utility value.

MINIMAX Algorithm

MINIMAX algorithm is a backtracking algorithm where it backtracks to pick the best move out of several choices. MINIMAX strategy follows the DFS (Depth-first search) concept. Here, we have two players MIN and MAX, and the game is played alternatively between them, i.e., when MAX made a move, then the next turn is of MIN. It means the move made by MAX is fixed and, he cannot change it. The same concept is followed in DFS strategy, i.e., we follow the same path and cannot change in the middle. That’s why in MINIMAX algorithm, instead of BFS, we follow DFS.

• Keep on generating the game tree/ search tree till a limit d.
• Compute the move using a heuristic function.
• Propagate the values from the leaf node till the current position following the minimax strategy.
• Make the best move from the choices.

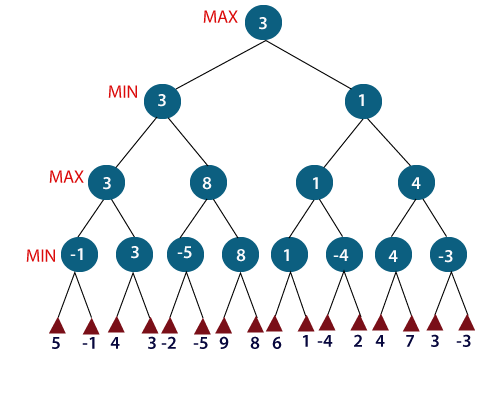
For example, in the above figure, the two players MAX and MIN are there. MAX starts the game by choosing one path and propagating all the nodes of that path. Now, MAX will backtrack to the initial node and choose the best path where his utility value will be the maximum. After this, its MIN chance. MIN will also propagate through a path and again will backtrack, but MIN will choose the path which could minimize MAX winning chances or the utility value.

So, if the level is minimizing, the node will accept the minimum value from the successor nodes. If the level is maximizing, the node will accept the maximum value from the successor.

2.6 Search for games

Searches in which two or more players with conflicting goals are trying to explore the same search space for the solution, are called adversarial searches, often known as Games.

Games are modeled as a Search problem and heuristic evaluation function, and these are the two main factors which help to model and solve games in AI.

Types of Games in AI:

• Perfect information: A game with the perfect information is that in which agents can look into the complete board. Agents have all the information about the game, and they can see each other moves also. Examples are Chess, Checkers, Go, etc.
• Imperfect information: If in a game agent do not have all information about the game and not aware with what's going on, such type of games are called the game with imperfect information, such as tic-tac-toe, Battleship, blind, Bridge, etc.
• Deterministic games: Deterministic games are those games which follow a strict pattern and set of rules for the games, and there is no randomness associated with them. Examples are chess, Checkers, Go, tic-tac-toe, etc.
• Non-deterministic games: Non-deterministic are those games which have various unpredictable events and has a factor of chance or luck. This factor of chance or luck is introduced by either dice or cards. These are random, and each action response is not fixed. Such games are also called as stochastic games.
  Example: Backgammon, Monopoly, Poker, etc.

Zero-Sum Game

• Zero-sum games are adversarial search which involves pure competition.
• In Zero-sum game each agent's gain or loss of utility is exactly balanced by the losses or gains of utility of another agent.
• One player of the game try to maximize one single value, while other player tries to minimize it.
• Each move by one player in the game is called as ply.
• Chess and tic-tac-toe are examples of a Zero-sum game.

Zero-sum game: Embedded thinking

The Zero-sum game involved embedded thinking in which one agent or player is trying to figure out:

• What to do.
• How to decide the move
• Needs to think about his opponent as well
• The opponent also thinks what to do

Each of the players is trying to find out the response of his opponent to their actions. This requires embedded thinking or backward reasoning to solve the game problems in AI.

Formalization of the problem:

A game can be defined as a type of search in AI which can be formalized of the following elements:

• Initial state: It specifies how the game is set up at the start.
• Player(s): It specifies which player has moved in the state space.
• Action(s): It returns the set of legal moves in state space.
• Result(s, a): It is the transition model, which specifies the result of moves in the state space.
• Terminal-Test(s): Terminal test is true if the game is over, else it is false at any case. The state where the game ends is called terminal states.
• Utility(s, p): A utility function gives the final numeric value for a game that ends in terminal states s for player p. It is also called payoff function. For Chess, the outcomes are a win, loss, or draw and its payoff values are +1, 0, ½. And for tic-tac-toe, utility values are +1, -1, and 0.

2.7 Alpha - Beta pruning

• Alpha-beta pruning is a modified version of the minimax algorithm. It is an optimization technique for the minimax algorithm.
• As we have seen in the minimax search algorithm that the number of game states it has to examine are exponential in depth of the tree. Since we cannot eliminate the exponent, but we can cut it to half. Hence there is a technique by which without checking each node of the game tree we can compute the correct minimax decision, and this technique is called pruning. This involves two threshold parameter Alpha and beta for future expansion, so it is called alpha-beta pruning. It is also called as Alpha-Beta Algorithm.
• Alpha-beta pruning can be applied at any depth of a tree, and sometimes it not only prunes the tree leaves but also entire sub-tree.
• The two-parameter can be defined as:
  1. Alpha: The best (highest-value) choice we have found so far at any point along the path of Maximiser. The initial value of alpha is -∞.
  2. Beta: The best (lowest-value) choice we have found so far at any point along the path of Minimizer. The initial value of beta is +∞.
• The Alpha-beta pruning to a standard minimax algorithm returns the same move as the standard algorithm does, but it removes all the nodes which are not really affecting the final decision but making algorithm slow. Hence by pruning these nodes, it makes the algorithm fast.

Note: To better understand this topic, kindly study the minimax algorithm.

Condition for Alpha-beta pruning:

The main condition which required for alpha-beta pruning is:

1. α>=β  

Key points about alpha-beta pruning:

• The Max player will only update the value of alpha.
• The Min player will only update the value of beta.
• While backtracking the tree, the node values will be passed to upper nodes instead of values of alpha and beta.
• We will only pass the alpha, beta values to the child nodes.

Pseudo-code for Alpha-beta Pruning:

1. Function minimax(node, depth, alpha, beta, maximizingPlayer) is  
2. If depth ==0 or node is a terminal node then  
3. Return static evaluation of node  
4.  
5. If MaximizingPlayer then      // for Maximizer Player  
6.   MaxEva= -infinity            
7.   For each child of node do  
8.   Eva= minimax(child, depth-1, alpha, beta, False)  
9.  MaxEva= max(maxEva, eva)   
10.  Alpha= max(alpha, maxEva)      
11.   If beta<=alpha  
12. Break  
13. Return maxEva  
14.    
15. Else                         // for Minimizer player  
16.   MinEva= +infinity   
17.   For each child of node do  
18.   Eva= minimax(child, depth-1, alpha, beta, true)  
19.   MinEva= min(minEva, eva)   
20.   Beta= min(beta, eva)  
21.    If beta<=alpha  
22.  Break          
23. Return minEva  

Working of Alpha-Beta Pruning:

Let's take an example of two-player search tree to understand the working of Alpha-beta pruning

Step 1: At the first step the, Max player will start first move from node A where α= -∞ and β= +∞, these value of alpha and beta passed down to node B where again α= -∞ and β= +∞, and Node B passes the same value to its child D.

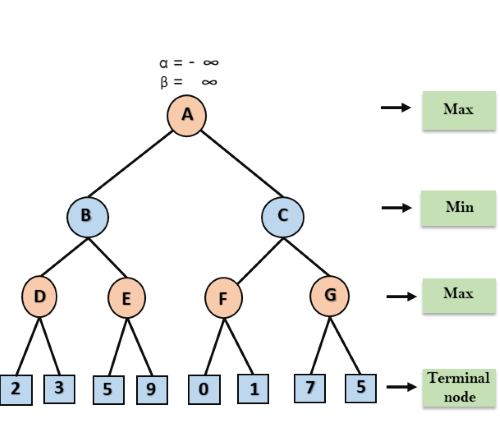
Step 2: At Node D, the value of α will be calculated as its turn for Max. The value of α is compared with firstly 2 and then 3, and the max (2, 3) = 3 will be the value of α at node D and node value will also 3.

Step 3: Now algorithm backtrack to node B, where the value of β will change as this is a turn of Min, Now β= +∞, will compare with the available subsequent nodes value, i.e. min (∞, 3) = 3, hence at node B now α= -∞, and β= 3.

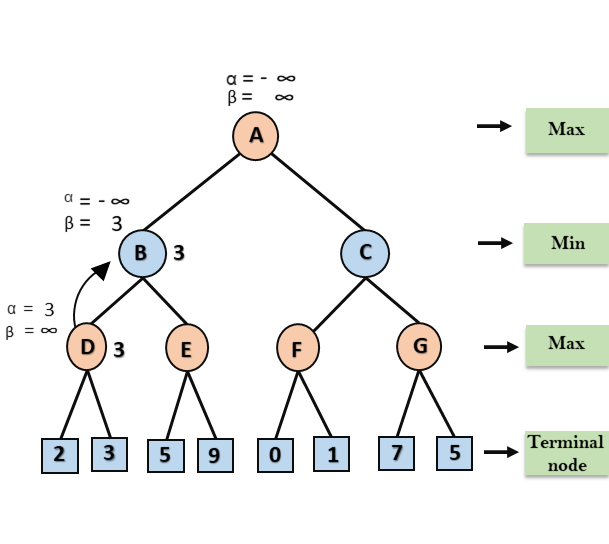
In the next step, algorithm traverse the next successor of Node B which is node E, and the values of α= -∞, and β= 3 will also be passed.

Step 4: At node E, Max will take its turn, and the value of alpha will change. The current value of alpha will be compared with 5, so max (-∞, 5) = 5, hence at node E α= 5 and β= 3, where α>=β, so the right successor of E will be pruned, and algorithm will not traverse it, and the value at node E will be 5.

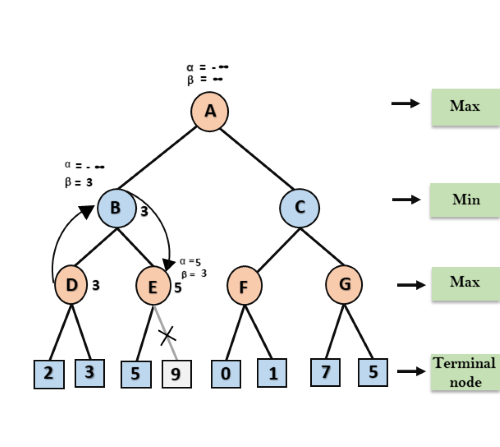
Step 5: At next step, algorithm again backtrack the tree, from node B to node A. At node A, the value of alpha will be changed the maximum available value is 3 as max (-∞, 3)= 3, and β= +∞, these two values now passes to right successor of A which is Node C.

At node C, α=3 and β= +∞, and the same values will be passed on to node F.

Step 6: At node F, again the value of α will be compared with left child which is 0, and max(3,0)= 3, and then compared with right child which is 1, and max(3,1)= 3 still α remains 3, but the node value of F will become 1.

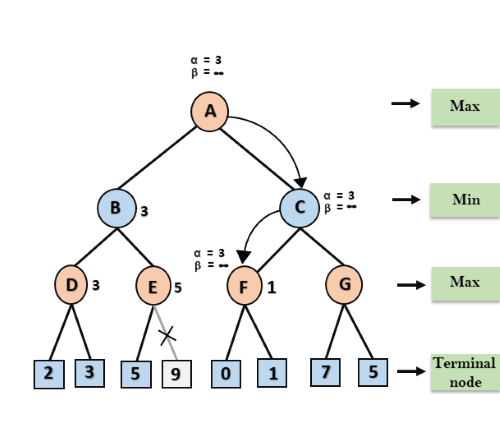
Step 7: Node F returns the node value 1 to node C, at C α= 3 and β= +∞, here the value of beta will be changed, it will compare with 1 so min (∞, 1) = 1. Now at C, α=3 and β= 1, and again it satisfies the condition α>=β, so the next child of C which is G will be pruned, and the algorithm will not compute the entire sub-tree G.

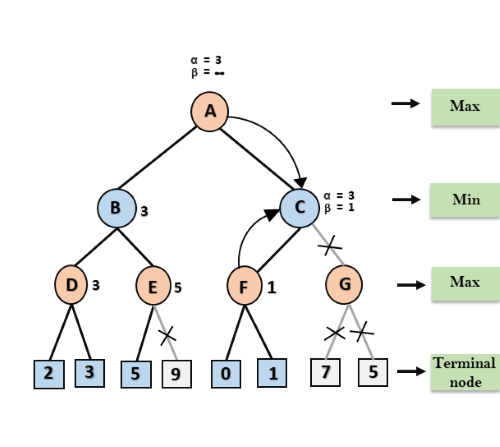
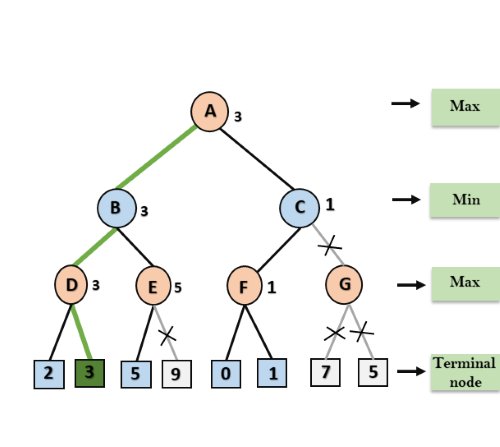
Step 8: C now returns the value of 1 to A here the best value for A is max (3, 1) = 3. Following is the final game tree which is the showing the nodes which are computed and nodes which has never computed. Hence the optimal value for the maximizer is 3 for this example.

Move Ordering in Alpha-Beta pruning:

The effectiveness of alpha-beta pruning is highly dependent on the order in which each node is examined. Move order is an important aspect of alpha-beta pruning.

It can be of two types:

• Worst ordering: In some cases, alpha-beta pruning algorithm does not prune any of the leaves of the tree, and works exactly as minimax algorithm. In this case, it also consumes more time because of alpha-beta factors, such a move of pruning is called worst ordering. In this case, the best move occurs on the right side of the tree. The time complexity for such an order is O(bm).
• Ideal ordering: The ideal ordering for alpha-beta pruning occurs when lots of pruning happens in the tree, and best moves occur at the left side of the tree. We apply DFS hence it first search left of the tree and go deep twice as minimax algorithm in the same amount of time. Complexity in ideal ordering is O(bm/2).

Rules to find good ordering:

Following are some rules to find good ordering in alpha-beta pruning:

• Occur the best move from the shallowest node.
• Order the nodes in the tree such that the best nodes are checked first.
• Use domain knowledge while finding the best move. Ex: for chess, try order: captures first, then threats, then forward moves, backward moves.
• We can bookkeep the states, as there is a possibility that states may repeat.

References:

1. Stuart Russell, Peter Norvig, “Artificial Intelligence – A Modern Approach”, Pearson Education

2. Elaine Rich and Kevin Knight, “Artificial Intelligence”, McGraw-Hill

3. E Charniak and D McDermott, “Introduction to Artificial Intelligence”, Pearson Education

4. Dan W. Patterson, “Artificial Intelligence and Expert Systems”, Prentice Hall of India