Unit - 3

Knowledge Representation & Reasoning

3.1 Propositional logic

Propositional logic (PL) is the simplest form of logic where all the statements are made by propositions. A proposition is a declarative statement which is either true or false. It is a technique of knowledge representation in logical and mathematical form.

Example:

1. a) It is Sunday.  
2. b) The Sun rises from West (False proposition)  
3. c) 3+3= 7(False proposition)  
4. d) 5 is a prime number.   

Following are some basic facts about propositional logic:

• Propositional logic is also called Boolean logic as it works on 0 and 1.
• In propositional logic, we use symbolic variables to represent the logic, and we can use any symbol for a representing a proposition, such A, B, C, P, Q, R, etc.
• Propositions can be either true or false, but it cannot be both.
• Propositional logic consists of an object, relations or function, and logical connectives.
• These connectives are also called logical operators.
• The propositions and connectives are the basic elements of the propositional logic.
• Connectives can be said as a logical operator which connects two sentences.
• A proposition formula which is always true is called tautology, and it is also called a valid sentence.
• A proposition formula which is always false is called Contradiction.
• A proposition formula which has both true and false values is called
• Statements which are questions, commands, or opinions are not propositions such as "Where is Rohini", "How are you", "What is your name", are not propositions.

Syntax of propositional logic:

The syntax of propositional logic defines the allowable sentences for the knowledge representation. There are two types of Propositions:

Atomic Propositions

Compound propositions

• Atomic Proposition: Atomic propositions are the simple propositions. It consists of a single proposition symbol. These are the sentences which must be either true or false.

Example:

1. a) 2+2 is 4, it is an atomic proposition as it is a true fact.  
2. b) "The Sun is cold" is also a proposition as it is a false fact.   

• Compound proposition: Compound propositions are constructed by combining simpler or atomic propositions, using parenthesis and logical connectives.

Example:

1. a) "It is raining today, and street is wet."  
2. b) "Ankit is a doctor, and his clinic is in Mumbai."   

Logical Connectives:

Logical connectives are used to connect two simpler propositions or representing a sentence logically. We can create compound propositions with the help of logical connectives. There are mainly five connectives, which are given as follows:

1. Negation: A sentence such as ¬ P is called negation of P. A literal can be either Positive literal or negative literal.
2. Conjunction: A sentence which has ∧connective such as, P ∧ Q is called a conjunction.
   Example: Rohan is intelligent and hardworking. It can be written as,
   P= Rohan is intelligent,
   Q= Rohan is hardworking. → P∧ Q.
3. Disjunction: A sentence which has ∨ connective, such as P ∨ Q. Is called disjunction, where P and Q are the propositions.
   Example: "Ritika is a doctor or Engineer",
   Here P= Ritika is Doctor. Q= Ritika is Doctor, so we can write it as P ∨ Q.
4. Implication: A sentence such as P → Q, is called an implication. Implications are also known as if-then rules. It can be represented as
   If it is raining, then the street is wet.
   Let P= It is raining, and Q= Street is wet, so it is represented as P → Q
5. Biconditional: A sentence such as P⇔ Q is a Biconditional sentence, example If I am breathing, then I am alive
   P= I am breathing, Q= I am alive, it can be represented as P ⇔ Q.

Following is the summarized table for Propositional Logic Connectives:

Connective symbols	Word	Technical term	Example
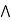	AND	Conjunction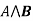
∨	OR	Disjunction	A∨B
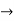	Implies	Implication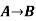
⟺	If and only if	Biconditional	A⟺B
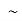or	Not	Negation	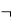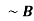Aor

Truth Table:

In propositional logic, we need to know the truth values of propositions in all possible scenarios. We can combine all the possible combination with logical connectives, and the representation of these combinations in a tabular format is called Truth table. Following are the truth table for all logical connectives:

For negation

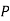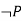True	False
False	True

For conjunction

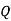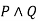True	True	True
True	False	False
False	True	False
False	False	False

For disjunction

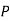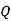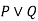True	True	True
False	True	True
True	False	True
False	False	False

For implication

P	Q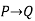
True	True	True
True	False	False
False	True	True
False	False	True

For Biconditional

Truth table with three propositions:

We can build a proposition composing three propositions P, Q, and R. This truth table is made-up of 8n Tuples as we have taken three proposition symbols.

P	Q	R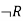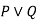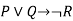
True	True	True	False	True	False
True	True	False	True	True	True
True	False	True	False	True	False
True	False	False	True	True	True
False	True	True	False	True	False
False	True	False	True	True	True
False	False	True	False	False	True
False	False	False	True	False	True

Precedence of connectives:

Just like arithmetic operators, there is a precedence order for propositional connectors or logical operators. This order should be followed while evaluating a propositional problem. Following is the list of the precedence order for operators:

Note: For better understanding use parenthesis to make sure of the correct interpretations. Such as ¬R∨ Q, It can be interpreted as (¬R) ∨ Q.

Logical equivalence:

Logical equivalence is one of the features of propositional logic. Two propositions are said to be logically equivalent if and only if the columns in the truth table are identical to each other.

Let's take two propositions A and B, so for logical equivalence, we can write it as A⇔B. In below truth table we can see that column for ¬A∨ B and A→B, are identical hence A is Equivalent to B

A	B
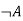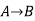T	T	F	T	T
T	F	F	F	F
F	T	T	T	T
F	F	T	T	T

Properties of Operators:

Commutativity:

• P∧ Q= Q ∧ P, or
• P ∨ Q = Q ∨ P.

Associativity:

• (P ∧ Q) ∧ R= P ∧ (Q ∧ R),
• (P ∨ Q) ∨ R= P ∨ (Q ∨ R)

Identity element:

• P ∧ True = P,
• P ∨ True= True.

Distributive:

• P∧ (Q ∨ R) = (P ∧ Q) ∨ (P ∧ R).
• P ∨ (Q ∧ R) = (P ∨ Q) ∧ (P ∨ R).

DE Morgan's Law:

• ¬ (P ∧ Q) = (¬P) ∨ (¬Q)
• ¬ (P ∨ Q) = (¬ P) ∧ (¬Q).

Double-negation elimination:

• ¬ (¬P) = P.

Limitations of Propositional logic:

• We cannot represent relations like ALL, some, or none with propositional logic. Example:

All the girls are intelligent.

Some apples are sweet.

• Propositional logic has limited expressive power.
• In propositional logic, we cannot describe statements in terms of their properties or logical relationships.

3.2 Theory of first order logic

In the topic of Propositional logic, we have seen that how to represent statements using propositional logic. But unfortunately, in propositional logic, we can only represent the facts, which are either true or false. PL is not sufficient to represent the complex sentences or natural language statements. The propositional logic has very limited expressive power. Consider the following sentence, which we cannot represent using PL logic.

"Some humans are intelligent", or

"Sachin likes cricket."

To represent the above statements, PL logic is not sufficient, so we required some more powerful logic, such as first-order logic.

First-Order logic:

• First-order logic is another way of knowledge representation in artificial intelligence. It is an extension to propositional logic.
• FOL is sufficiently expressive to represent the natural language statements in a concise way.
• First-order logic is also known as Predicate logic or First-order predicate logic. First-order logic is a powerful language that develops information about the objects in a more easy way and can also express the relationship between those objects.
• First-order logic (like natural language) does not only assume that the world contains facts like propositional logic but also assumes the following things in the world:
  • Objects: A, B, people, numbers, colors, wars, theories, squares, pits, Wumpus.
  • Relations: It can be unary relation such as: red, round, is adjacent, or n-any relation such as: the sister of, brother of, has color, comes between
  • Function: Father of, best friend, third inning of, end of, ......
• As a natural language, first-order logic also has two main parts:

Syntax of First-Order logic:

The syntax of FOL determines which collection of symbols is a logical expression in first-order logic. The basic syntactic elements of first-order logic are symbols. We write statements in short-hand notation in FOL.

Basic Elements of First-order logic:

Following are the basic elements of FOL syntax:

Atomic sentences:

• Atomic sentences are the most basic sentences of first-order logic. These sentences are formed from a predicate symbol followed by a parenthesis with a sequence of terms.
• We can represent atomic sentences as Predicate (term1, term2, ......, term n).

Example: Ravi and Ajay are brothers: => Brothers(Ravi, Ajay).
Chinky is a cat: => cat (Chinky).

Complex Sentences:

• Complex sentences are made by combining atomic sentences using connectives.

First-order logic statements can be divided into two parts:

• Subject: Subject is the main part of the statement.
• Predicate: A predicate can be defined as a relation, which binds two atoms together in a statement.

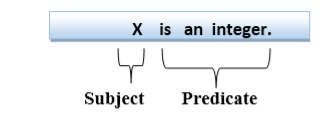
Consider the statement: "x is an integer.", it consists of two parts, the first part x is the subject of the statement and second part "is an integer," is known as a predicate.

Quantifiers in First-order logic:

• A quantifier is a language element which generates quantification, and quantification specifies the quantity of specimen in the universe of discourse.
• These are the symbols that permit to determine or identify the range and scope of the variable in the logical expression. There are two types of quantifier:

Universal Quantifier, (for all, everyone, everything)

Existential quantifier, (for some, at least one).

Universal Quantifier:

Universal quantifier is a symbol of logical representation, which specifies that the statement within its range is true for everything or every instance of a particular thing.

The Universal quantifier is represented by a symbol ∀, which resembles an inverted A.

Note: In universal quantifier we use implication "→".

If x is a variable, then ∀x is read as:

For all x

For each x

For every x.

Example:

All man drink coffee.

Let a variable x which refers to a cat so all x can be represented in UOD as below:

∀x man(x) → drink (x, coffee).

It will be read as: There are all x where x is a man who drink coffee.

Existential Quantifier:

Existential quantifiers are the type of quantifiers, which express that the statement within its scope is true for at least one instance of something.

It is denoted by the logical operator ∃, which resembles as inverted E. When it is used with a predicate variable then it is called as an existential quantifier.

Note: In Existential quantifier we always use AND or Conjunction symbol (∧).

If x is a variable, then existential quantifier will be ∃x or ∃(x). And it will be read as:

There exists a 'x.'

For some 'x.'

For at least one 'x.'

Example:

Some boys are intelligent.

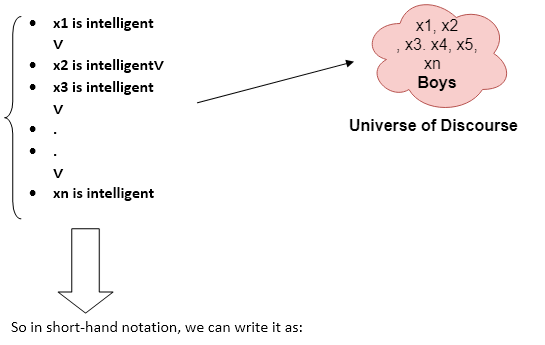
∃x: boys(x) ∧ intelligent(x)

It will be read as: There are some x where x is a boy who is intelligent.

Points to remember:

• The main connective for universal quantifier ∀ is implication →.
• The main connective for existential quantifier ∃ is and ∧.

Properties of Quantifiers:

• In universal quantifier, ∀x∀y is similar to ∀y∀x.
• In Existential quantifier, ∃x∃y is similar to ∃y∃x.
• ∃x∀y is not similar to ∀y∃x.

Some Examples of FOL using quantifier:

1. All birds fly.
In this question the predicate is "fly(bird)."
And since there are all birds who fly so it will be represented as follows.
              ∀x bird(x) →fly(x).

2. Every man respects his parent.
In this question, the predicate is "respect(x, y)," where x=man, and y= parent.
Since there is every man so will use ∀, and it will be represented as follows:
              ∀x man(x) → respects (x, parent).

3. Some boys play cricket.
In this question, the predicate is "play(x, y)," where x= boys, and y= game. Since there are some boys so we will use ∃, and it will be represented as:
              ∃x boys(x) → play(x, cricket).

4. Not all students like both Mathematics and Science.
In this question, the predicate is "like(x, y)," where x= student, and y= subject.
Since there are not all students, so we will use ∀ with negation, so following representation for this:
              ¬∀ (x) [ student(x) → like(x, Mathematics) ∧ like(x, Science)].

5. Only one student failed in Mathematics.
In this question, the predicate is "failed(x, y)," where x= student, and y= subject.
Since there is only one student who failed in Mathematics, so we will use following representation for this:
              ∃(x) [ student(x) → failed (x, Mathematics) ∧∀ (y) [¬(x==y) ∧ student(y) → ¬failed (x, Mathematics)].

Free and Bound Variables:

The quantifiers interact with variables which appear in a suitable way. There are two types of variables in First-order logic which are given below:

Free Variable: A variable is said to be a free variable in a formula if it occurs outside the scope of the quantifier.

Example: ∀x ∃(y)[P (x, y, z)], where z is a free variable.

Bound Variable: A variable is said to be a bound variable in a formula if it occurs within the scope of the quantifier.

Example: ∀x [A (x) B( y)], here x and y are the bound variables.

3.3 Inference in First order logic

Inference in First-Order Logic is used to deduce new facts or sentences from existing sentences. Before understanding the FOL inference rule, let's understand some basic terminologies used in FOL.

Substitution:

Substitution is a fundamental operation performed on terms and formulas. It occurs in all inference systems in first-order logic. The substitution is complex in the presence of quantifiers in FOL. If we write F[a/x], so it refers to substitute a constant "a" in place of variable "x".

Note: First-order logic is capable of expressing facts about some or all objects in the universe.

Equality:

First-Order logic does not only use predicate and terms for making atomic sentences but also uses another way, which is equality in FOL. For this, we can use equality symbols which specify that the two terms refer to the same object.

Example: Brother (John) = Smith.

As in the above example, the object referred by the Brother (John) is similar to the object referred by Smith. The equality symbol can also be used with negation to represent that two terms are not the same objects.

Example: ￢(x=y) which is equivalent to x ≠y.

FOL inference rules for quantifier:

As propositional logic we also have inference rules in first-order logic, so following are some basic inference rules in FOL:

Universal Generalization

Universal Instantiation

Existential Instantiation

Existential introduction

1. Universal Generalization:

• Universal generalization is a valid inference rule which states that if premise P(c) is true for any arbitrary element c in the universe of discourse, then we can have a conclusion as ∀ x P(x).
• It can be represented as: .
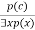• This rule can be used if we want to show that every element has a similar property.
• In this rule, x must not appear as a free variable.

Example: Let's represent, P(c): "A byte contains 8 bits", so for ∀ x P(x) "All bytes contain 8 bits.", it will also be true.

2. Universal Instantiation:

• Universal instantiation is also called as universal elimination or UI is a valid inference rule. It can be applied multiple times to add new sentences.
• The new KB is logically equivalent to the previous KB.
• As per UI, we can infer any sentence obtained by substituting a ground term for the variable.
• The UI rule state that we can infer any sentence P(c) by substituting a ground term c (a constant within domain x) from ∀ x P(x) for any object in the universe of discourse.
• It can be represented as:.

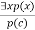Example:1.

IF "Every person like ice-cream"=>∀x P(x) so we can infer that
"John likes ice-cream" => P(c)

Example: 2.

Let's take a famous example,

"All kings who are greedy are Evil." So let our knowledge base contains this detail as in the form of FOL:

∀x king(x) ∧ greedy (x) → Evil (x),

So from this information, we can infer any of the following statements using Universal Instantiation:

King(John) ∧ Greedy (John) → Evil (John),

King(Richard) ∧ Greedy (Richard) → Evil (Richard),

King(Father(John)) ∧ Greedy (Father(John)) → Evil (Father(John)),

3. Existential Instantiation:

• Existential instantiation is also called as Existential Elimination, which is a valid inference rule in first-order logic.
• It can be applied only once to replace the existential sentence.
• The new KB is not logically equivalent to old KB, but it will be satisfiable if old KB was satisfiable.
• This rule states that one can infer P(c) from the formula given in the form of ∃x P(x) for a new constant symbol c.
• The restriction with this rule is that c used in the rule must be a new term for which P(c ) is true.
• It can be represented as:

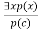
Example:

From the given sentence: ∃x Crown(x) ∧ OnHead(x, John),

So we can infer: Crown(K) ∧ OnHead(K, John), as long as K does not appear in the knowledge base.

• The above used K is a constant symbol, which is called Skolem constant.
• The Existential instantiation is a special case of Skolemization process.

4. Existential introduction

• An existential introduction is also known as an existential generalization, which is a valid inference rule in first-order logic.
• This rule states that if there is some element c in the universe of discourse which has a property P, then we can infer that there exists something in the universe which has the property P.
• It can be represented as:
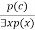
• Example: Let's say that,
  "Priyanka got good marks in English."
  "Therefore, someone got good marks in English."

Generalized Modus Ponens Rule:

For the inference process in FOL, we have a single inference rule which is called Generalized Modus Ponens. It is lifted version of Modus ponens.

Generalized Modus Ponens can be summarized as, " P implies Q and P is asserted to be true, therefore Q must be True."

According to Modus Ponens, for atomic sentences pi, pi', q. Where there is a substitution θ such that SUBST (θ, pi',) = SUBST(θ, pi), it can be represented as:

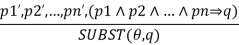
Example:

We will use this rule for Kings are evil, so we will find some x such that x is king, and x is greedy so we can infer that x is evil.

1. Here let say, p1' is king(John)        p1 is king(x)  
2. p2' is Greedy(y)                       p2 is Greedy(x)  
3. θ is {x/John, y/John}                  q is evil(x)  
4. SUBST(θ, q).                                                        

3.4 Forward & Backward chaining

Forward chaining is also known as forward deduction or forward reasoning when using an inference engine. Forward chaining is a method of reasoning that begins with atomic sentences in a knowledge base and uses inference rules to extract more information in the forward direction until a goal is reached.

Beginning with known facts, the Forward-chaining algorithm activates all rules with satisfied premises and adds their conclusion to the known facts. This procedure is repeated until the problem is resolved.

It's a method of inference that starts with sentences in the knowledge base and generates new conclusions that may then be utilized to construct subsequent inferences. It's a plan based on data. We start with known facts and organize or chain them to get to the query. The ponens modus operandi is used. It begins with the data that is already accessible and then uses inference rules to extract new data until the goal is achieved.

Example: To determine the color of Fritz, a pet who croaks and eats flies, for example. The Knowledge Base contains the following rules:

If X croaks and eats flies — → Then X is a frog.

If X sings — → Then X is a bird.

If X is a frog — → Then X is green.

If x is a bird — -> Then X is blue.

In the KB, croaks and eating insects are found. As a result, we arrive at rule 1, which has an antecedent that matches our facts. The KB is updated to reflect the outcome of rule 1, which is that X is a frog. The KB is reviewed again, and rule 3 is chosen because its antecedent (X is a frog) corresponds to our newly confirmed evidence. The new result is then recorded in the knowledge base (i.e., X is green). As a result, we were able to determine the pet's color based on the fact that it croaks and eats flies.

Properties of forward chaining

●      It is a down-up approach since it moves from bottom to top.

●      It is a process for reaching a conclusion based on existing facts or data by beginning at the beginning and working one's way to the end.

●      Because it helps us to achieve our goal by exploiting current data, forward-chaining is also known as data-driven.

●      The forward-chaining methodology is often used in expert systems, such as CLIPS, business, and production rule systems.

Backward chaining

Backward-chaining is also known as backward deduction or backward reasoning when using an inference engine. A backward chaining algorithm is a style of reasoning that starts with the goal and works backwards through rules to find facts that support it.

It's an inference approach that starts with the goal. We look for implication phrases that will help us reach a conclusion and justify its premises. It is an approach for proving theorems that is goal-oriented.

Example: Fritz, a pet that croaks and eats flies, needs his color determined. The Knowledge Base contains the following rules:

If X croaks and eats flies — → Then X is a frog.

If X sings — → Then X is a bird.

If X is a frog — → Then X is green.

If x is a bird — -> Then X is blue.

The third and fourth rules were chosen because they best fit our goal of determining the color of the pet. For example, X may be green or blue. Both the antecedents of the rules, X is a frog and X is a bird, are added to the target list. The first two rules were chosen because their implications correlate to the newly added goals, namely, X is a frog or X is a bird.

Because the antecedent (If X croaks and eats flies) is true/given, we can derive that Fritz is a frog. If it's a frog, Fritz is green, and if it's a bird, Fritz is blue, completing the goal of determining the pet's color.

Properties of backward chaining

●      A top-down strategy is what it's called.

●      Backward-chaining employs the modus ponens inference rule.

●      In backward chaining, the goal is broken down into sub-goals or sub-goals to ensure that the facts are true.

●      Because a list of objectives decides which rules are chosen and implemented, it's known as a goal-driven strategy.

●      The backward-chaining approach is utilized in game theory, automated theorem proving tools, inference engines, proof assistants, and other AI applications.

●      The backward-chaining method relied heavily on a depth-first search strategy for proof.

Key takeaway

1. Forward chaining is a type of reasoning that starts with atomic sentences in a knowledge base and uses inference rules to extract more material in the forward direction until a goal is attained.
2. The Forward-chaining algorithm begins with known facts, then activates all rules with satisfied premises and adds their conclusion to the known facts.
3. A backward chaining algorithm is a type of reasoning that begins with the objective and goes backward, chaining via rules to discover known facts that support it.

3.5 Resolution

Resolution is a theorem proving technique that proceeds by building refutation proofs, i.e., proofs by contradictions. It was invented by a Mathematician John Alan Robinson in the year 1965.

Resolution is used, if there are various statements are given, and we need to prove a conclusion of those statements. Unification is a key concept in proofs by resolutions. Resolution is a single inference rule which can efficiently operate on the conjunctive normal form or clausal form.

Clause: Disjunction of literals (an atomic sentence) is called a clause. It is also known as a unit clause.

Conjunctive Normal Form: A sentence represented as a conjunction of clauses is said to be conjunctive normal form or CNF.

Note: To better understand this topic, firstly learns the FOL in AI.

The resolution inference rule:

The resolution rule for first-order logic is simply a lifted version of the propositional rule. Resolution can resolve two clauses if they contain complementary literals, which are assumed to be standardized apart so that they share no variables.

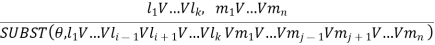
Where li and mj are complementary literals.

This rule is also called the binary resolution rule because it only resolves exactly two literals.

Example:

We can resolve two clauses which are given below:

[Animal (g(x) V Loves (f(x), x)] and [￢ Loves(a, b) V ￢Kills(a, b)]

Where two complimentary literals are: Loves (f(x), x) and ￢ Loves (a, b)

These literals can be unified with unifier θ= [a/f(x), and b/x], and it will generate a resolvent clause:

[Animal (g(x) V ￢ Kills(f(x), x)].

Steps for Resolution:

1. Conversion of facts into first-order logic.
2. Convert FOL statements into CNF
3. Negate the statement which needs to prove (proof by contradiction)
4. Draw resolution graph (unification).

To better understand all the above steps, we will take an example in which we will apply resolution.

Example:

John likes all kind of food.

Apple and vegetable are food

Anything anyone eats and not killed is food.

Anil eats peanuts and still alive

1. Harry eats everything that Anil eats.
   Prove by resolution that:

John likes peanuts.

Step-1: Conversion of Facts into FOL

In the first step we will convert all the given statements into its first order logic.

a. 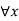: food(x) 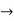likes (John,x)

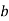. Food (Apple) 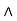food (vegetables)

c. 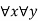: eats(x,y)killed(x)(y)

d. Eats(Anil, peanuts) alive(Anil)

e. 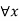: eats(Anil,x) 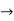eats(Harry,x)

f. 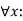killed(x)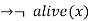

g. 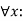alive(x)

h. Likes(John, Peanusts)

Here f and g are added predicates.

Step-2: Conversion of FOL into CNF

In First order logic resolution, it is required to convert the FOL into CNF as CNF form makes easier for resolution proofs.

Eliminate all implication (→) and rewrite

1. ∀x ¬ food(x) V likes(John, x)
2. Food(Apple) Λ food(vegetables)
3. ∀x ∀y ¬ [eats(x, y) Λ¬ killed(x)] V food(y)
4. Eats (Anil, Peanuts) Λ alive(Anil)
5. ∀x ¬ eats(Anil, x) V eats(Harry, x)
6. ∀x¬ [¬ killed(x) ] V alive(x)
7. ∀x ¬ alive(x) V ¬ killed(x)
8. Likes(John, Peanuts).

Move negation (¬)inwards and rewrite

9.     ∀x ¬ food(x) V likes(John, x)

10. food(Apple) Λ food(vegetables)

11. ∀x ∀y ¬ eats(x, y) V killed(x) V food(y)

12. eats (Anil, Peanuts) Λ alive(Anil)

13. ∀x ¬ eats(Anil, x) V eats(Harry, x)

14. ∀x ¬killed(x) ] V alive(x)

15. ∀x ¬ alive(x) V ¬ killed(x)

16. likes(John, Peanuts).

Rename variables or standardize variables

17. ∀x ¬ food(x) V likes(John, x)

18. food(Apple) Λ food(vegetables)

19. ∀y ∀z ¬ eats(y, z) V killed(y) V food(z)

20. eats (Anil, Peanuts) Λ alive(Anil)

21. ∀w¬ eats(Anil, w) V eats(Harry, w)

22. ∀g ¬killed(g) ] V alive(g)

23. ∀k ¬ alive(k) V ¬ killed(k)

24. likes(John, Peanuts).

• Eliminate existential instantiation quantifier by elimination.
  In this step, we will eliminate existential quantifier ∃, and this process is known as Skolemization. But in this example problem since there is no existential quantifier so all the statements will remain same in this step.
• Drop Universal quantifiers.
  In this step we will drop all universal quantifier since all the statements are not implicitly quantified so we don't need it.
  1. ¬ food(x) V likes(John, x)
  2. Food(Apple)
  3. Food(vegetables)
  4. ¬ eats(y, z) V killed(y) V food(z)
  5. Eats (Anil, Peanuts)
  6. Alive(Anil)
  7. ¬ eats(Anil, w) V eats(Harry, w)
  8. Killed(g) V alive(g)
  9. ¬ alive(k) V ¬ killed(k)
  10. Likes(John, Peanuts).

Note: Statements "food(Apple) Λ food(vegetables)" and "eats (Anil, Peanuts) Λ alive(Anil)" can be written in two separate statements.

• Distribute conjunction ∧ over disjunction ¬.
  This step will not make any change in this problem.

Step-3: Negate the statement to be proved

In this statement, we will apply negation to the conclusion statements, which will be written as ¬likes(John, Peanuts)

Step-4: Draw Resolution graph:

Now in this step, we will solve the problem by resolution tree using substitution. For the above problem, it will be given as follows:

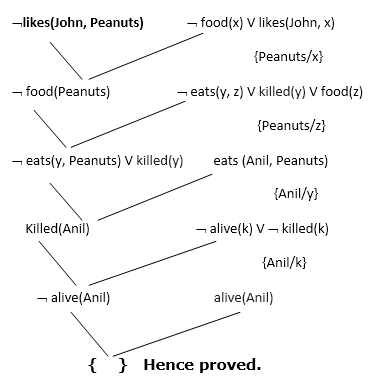
Hence the negation of the conclusion has been proved as a complete contradiction with the given set of statements.

Explanation of Resolution graph:

• In the first step of resolution graph, ¬likes(John, Peanuts) , and likes(John, x) get resolved(cancelled) by substitution of {Peanuts/x}, and we are left with ¬ food(Peanuts)
• In the second step of the resolution graph, ¬ food(Peanuts) , and food(z) get resolved (cancelled) by substitution of { Peanuts/z}, and we are left with ¬ eats(y, Peanuts) V killed(y) .
• In the third step of the resolution graph, ¬ eats(y, Peanuts) and eats (Anil, Peanuts) get resolved by substitution {Anil/y}, and we are left with Killed(Anil) .
• In the fourth step of the resolution graph, Killed(Anil) and ¬ killed(k) get resolve by substitution {Anil/k}, and we are left with ¬ alive(Anil) .
• In the last step of the resolution graph ¬ alive(Anil) and alive(Anil) get resolved.

3.6 Probabilistic reasoning

Probabilistic reasoning is a way of knowledge representation where we apply the concept of probability to indicate the uncertainty in knowledge. In probabilistic reasoning, we combine probability theory with logic to handle the uncertainty.

We use probability in probabilistic reasoning because it provides a way to handle the uncertainty that is the result of someone's laziness and ignorance.

In the real world, there are lots of scenarios, where the certainty of something is not confirmed, such as "It will rain today," "behavior of someone for some situations," "A match between two teams or two players." These are probable sentences for which we can assume that it will happen but not sure about it, so here we use probabilistic reasoning.

Need of probabilistic reasoning in AI:

• When there are unpredictable outcomes.
• When specifications or possibilities of predicates becomes too large to handle.
• When an unknown error occurs during an experiment.

In probabilistic reasoning, there are two ways to solve problems with uncertain knowledge:

Bayes' rule

Bayesian Statistics

As probabilistic reasoning uses probability and related terms, so before understanding probabilistic reasoning, let's understand some common terms:

Probability: Probability can be defined as a chance that an uncertain event will occur. It is the numerical measure of the likelihood that an event will occur. The value of probability always remains between 0 and 1 that represent ideal uncertainties.

1. 0 ≤ P(A) ≤ 1, where P(A) is the probability of an event A.  

1. P(A) = 0, indicates total uncertainty in an event A.   

1. P(A) =1, indicates total certainty in an event A.    

We can find the probability of an uncertain event by using the below formula.

Probability of occurrence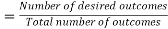

• P(¬A) = probability of a not happening event.
• P(¬A) + P(A) = 1.

Event: Each possible outcome of a variable is called an event.

Sample space: The collection of all possible events is called sample space.

Random variables: Random variables are used to represent the events and objects in the real world.

Prior probability: The prior probability of an event is probability computed before observing new information.

Posterior Probability: The probability that is calculated after all evidence or information has taken into account. It is a combination of prior probability and new information.

Conditional probability:

Conditional probability is a probability of occurring an event when another event has already happened.

Let's suppose, we want to calculate the event A when event B has already occurred, "the probability of A under the conditions of B", it can be written as:

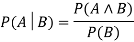
Where P(A⋀B)= Joint probability of a and B

P(B)= Marginal probability of B.

If the probability of A is given and we need to find the probability of B, then it will be given as:

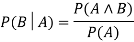
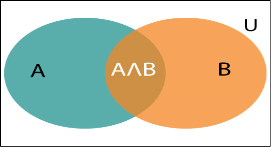
It can be explained by using the below Venn diagram, where B is occurred event, so sample space will be reduced to set B, and now we can only calculate event A when event B is already occurred by dividing the probability of P(A⋀B) by P( B ).

Example:

In a class, there are 70% of the students who like English and 40% of the students who likes English and mathematics, and then what is the percent of students those who like English also like mathematics?

Solution:

Let, A is an event that a student likes Mathematics

B is an event that a student likes English.

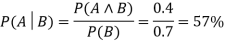
Hence, 57% are the students who like English also like Mathematics.

3.7 Utility theory

The main idea of utility theory is really simple an agent's preferences over possible outcomes can be captured by a function that maps these outcomes to a real number the higher the number the more that agent likes that outcome. The function is called a utility function.

For example, we could say that my utility for owning various items is.

u(apple) = 10

u(orange) = 12

u(basketball) = 4

u(macbookpro) = 45

Economists (usually) consider humans as utility-maximizing agents. That is, we are always trying to maximize our internal utility function.

Note- The agents use the utility theory for making decisions. It is the mapping from lotteries to the real numbers. An agent is supposed to have various preferences and can choose the one which best fits his necessity.

Utility scales and Utility assessments

To help an agent in making decisions and behave accordingly, we need to build a decision-theoretic system. For this, we need to understand the utility function. This process is known as preference elicitation. In this, the agents are provided with some choices and using the observed preferences, the respected utility function is chosen. Generally, there is no scale for the utility function. But a scale can be established by fixing the boiling and freezing point of water.

Thus, the utility is fixed as.

U(S)=uT for best possible cases

U(S)= u?  for worst possible cases.

A normalized utility function uses a utility scale with value uT=1, and u? =0. For example, a utility scale between uT and u?  is given. Thereby an agent can choose a utility value between any prize Z and the standard lottery [p, u_; (1?p), u?]. Here, p denotes the probability which is adjusted until the agent is adequate between Z and the standard lottery.

Money Utility

Economics is the root of utility theory. It is the most demanding thing in human life. Therefore, an agent prefers more money to less, where all other things remain equal. The agent exhibits a monotonic preference (more is preferred over less) for getting more money. In order to evaluate the more utility value, the agent calculates the Expected Monetary Value(EMV) of that particular thing. But this does not mean that choosing a monotonic value is the right decision always.

Multi-attribute utility functions

Multi-attribute utility functions include those problems whose outcomes are categorized by two or more attributes. Such problems are handled by multi-attribute utility theory.

Terminology used

• Dominance:  If there are two choices say A and B, where A is more effective than B. It means that A will be chosen. Thus, A will dominate B. Therefore, multi-attribute utility function offers two types of dominance:

• Strict Dominance: If there are two websites T and D, where the cost of T is less and provides better service than D. Obviously, the customer will prefer T rather than D. Therefore, T strictly dominates D. Here, the attribute values are known.

• Stochastic Dominance:  It is a generalized approach where the attribute value is unknown. It frequently occurs in real problems. Here, a uniform distribution is given, where that choice is picked, which stochastically dominates the other choices. The exact relationship can be viewed by examing the cumulative distribution of the attributes.

• Preference Structure: Representation theorems are used to show that an agent with a preference structure has a utility function as:

U(x1, . . . , xn) = F[f1(x1), . . . , fn(xn)],

Where F indicates any arithmetic function such as an addition function.

Note preference can be done in two ways

• Preference without uncertainty-The preference where two attributes are preferentially independent of the third attribute. It is because the preference between the outcomes of the first two attributes does not depend on the third one.

• Preference with uncertainty- This refers to the concept of preference structure with uncertainty. Here, the utility independence extends the preference independence where a set of attributes X is utility independent of another Y set of attributes, only if the value of attribute in X set is independent of Y set attribute value. A set is said to be mutually utility independent (MUI) if each subset is utility-independent of the remaining attribute.

3.8 Hidden Markov Models (HMM)

The Hidden Markov Model (HMM) is an analytical Model where the system being modelled is considered a Markov process with hidden or unobserved states. Machine learning and pattern recognition applications, like gesture recognition & speech handwriting, are applications of the Hidden Markov Model.

HMM, Hidden Markov Model enables us to speak about observed or visible events and hidden events in our probabilistic model.

The below diagram depicts the interaction between two ‘HIDDEN’ states, ‘Rainy’ and ‘Sunny’ in this case. ‘Walk’, ‘Shop’, and ‘Clean’ in the below diagram are known as data, referred to as OBSERVATIONS

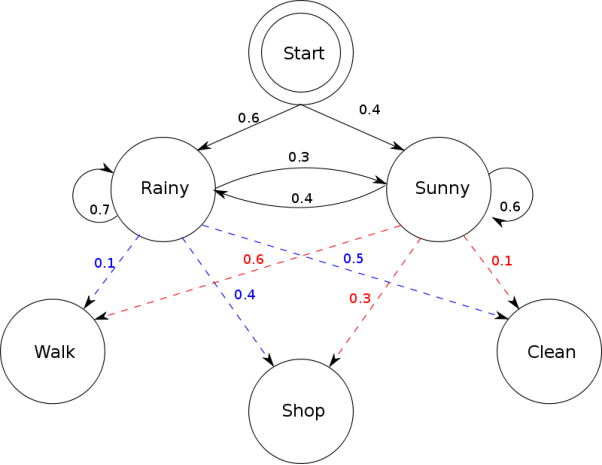
Markov Chain – three states (snow, rain, and sunshine)

P – the transition probability matrix

q – the initial probabilities 

The above example represents the invisible Markov Chain; for instance, we are at home and cannot see the weather. However, we can feel the temperature inside the rooms at home.

There will be two possible observations, hot and cold, where.

P(Hot|Snow) = 0, P(Cold|Snow) = 1

P(Hot|Rain) = 0.2, P(Cold|Rain) = 0.8

P(Hot|Sunshine) = 0.7, P(Cold|Sunshine) = 0.3

Example on HMM to compute the probability of whether we will feel cold for two consecutive days; there are 3*3=9 possibilities or options for the underlying Markov states in these two days.

P((Cold, Cold), P(Rain, Snow)) = P((Cold, Cold)|(Rain, Snow)).P(Rain, Snow) = P(Cold|Rain).P(Cold|Snow).P(Snow|Rain).P(Rain) = 0.8 . 1 . 0.1 . 0.2 = 0.016

3.9 Bayesian Networks

Bayesian belief network is key computer technology for dealing with probabilistic events and to solve a problem which has uncertainty. We can define a Bayesian network as:

"A Bayesian network is a probabilistic graphical model which represents a set of variables and their conditional dependencies using a directed acyclic graph."

It is also called a Bayes network, belief network, decision network, or Bayesian model.

Bayesian networks are probabilistic, because these networks are built from a probability distribution, and also use probability theory for prediction and anomaly detection.

Real world applications are probabilistic in nature, and to represent the relationship between multiple events, we need a Bayesian network. It can also be used in various tasks including prediction, anomaly detection, diagnostics, automated insight, reasoning, time series prediction, and decision making under uncertainty.

Bayesian Network can be used for building models from data and experts opinions, and it consists of two parts:

Directed Acyclic Graph

Table of conditional probabilities.

The generalized form of Bayesian network that represents and solve decision problems under uncertain knowledge is known as an Influence diagram.

A Bayesian network graph is made up of nodes and Arcs (directed links), where:

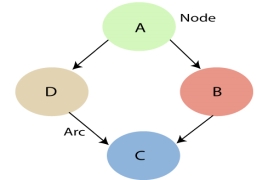
• Each node corresponds to the random variables, and a variable can be continuous or discrete.
• Arc or directed arrows represent the causal relationship or conditional probabilities between random variables. These directed links or arrows connect the pair of nodes in the graph.
  These links represent that one node directly influence the other node, and if there is no directed link that means that nodes are independent with each other

In the above diagram, A, B, C, and D are random variables represented by the nodes of the network graph.

If we are considering node B, which is connected with node A by a directed arrow, then node A is called the parent of Node B.

Node C is independent of node A.

Note: The Bayesian network graph does not contain any cyclic graph. Hence, it is known as a directed acyclic graph or DAG.

The Bayesian network has mainly two components:

Causal Component

Actual numbers

Each node in the Bayesian network has condition probability distribution P(Xi |Parent(Xi) ), which determines the effect of the parent on that node.

Bayesian network is based on Joint probability distribution and conditional probability. So let's first understand the joint probability distribution:

Joint probability distribution:

If we have variables x1, x2, x3,....., xn, then the probabilities of a different combination of x1, x2, x3.. Xn, are known as Joint probability distribution.

P[x1, x2, x3,....., xn], it can be written as the following way in terms of the joint probability distribution.

= P[x1| x2, x3,....., xn]P[x2, x3,....., xn]

= P[x1| x2, x3,....., xn]P[x2|x3,....., xn]....P[xn-1|xn]P[xn].

In general, for each variable Xi, we can write the equation as:

P(Xi|Xi-1,........., X1) = P(Xi |Parents(Xi ))

Explanation of Bayesian network:

Let's understand the Bayesian network through an example by creating a directed acyclic graph:

Example: Harry installed a new burglar alarm at his home to detect burglary. The alarm reliably responds at detecting a burglary but also responds for minor earthquakes. Harry has two neighbors David and Sophia, who have taken a responsibility to inform Harry at work when they hear the alarm. David always calls Harry when he hears the alarm, but sometimes he got confused with the phone ringing and calls at that time too. On the other hand, Sophia likes to listen to high music, so sometimes she misses to hear the alarm. Here we would like to compute the probability of Burglary Alarm.

Problem:

Calculate the probability that alarm has sounded, but there is neither a burglary, nor an earthquake occurred, and David and Sophia both called the Harry.

Solution:

• The Bayesian network for the above problem is given below. The network structure is showing that burglary and earthquake is the parent node of the alarm and directly affecting the probability of alarm's going off, but David and Sophia's calls depend on alarm probability.
• The network is representing that our assumptions do not directly perceive the burglary and also do not notice the minor earthquake, and they also not confer before calling.
• The conditional distributions for each node are given as conditional probabilities table or CPT.
• Each row in the CPT must be sum to 1 because all the entries in the table represent an exhaustive set of cases for the variable.
• In CPT, a boolean variable with k boolean parents contains 2K probabilities. Hence, if there are two parents, then CPT will contain 4 probability values

List of all events occurring in this network:

Burglary (B)

Earthquake(E)

Alarm(A)

David Calls(D)

Sophia calls(S)

We can write the events of problem statement in the form of probability: P[D, S, A, B, E], can rewrite the above probability statement using joint probability distribution:

P[D, S, A, B, E]= P[D | S, A, B, E]. P[S, A, B, E]

=P[D | S, A, B, E]. P[S | A, B, E]. P[A, B, E]

= P [D| A]. P [ S| A, B, E]. P[ A, B, E]

= P[D | A]. P[ S | A]. P[A| B, E]. P[B, E]

= P[D | A ]. P[S | A]. P[A| B, E]. P[B |E]. P[E]

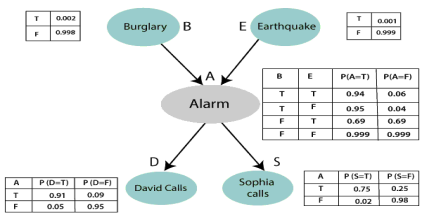
Let's take the observed probability for the Burglary and earthquake component:

P(B= True) = 0.002, which is the probability of burglary.

P(B= False)= 0.998, which is the probability of no burglary.

P(E= True)= 0.001, which is the probability of a minor earthquake

P(E= False)= 0.999, Which is the probability that an earthquake not occurred.

We can provide the conditional probabilities as per the below tables:

Conditional probability table for Alarm A:

The Conditional probability of Alarm A depends on Burglar and earthquake:

Conditional probability table for David Calls:

The Conditional probability of David that he will call depends on the probability of Alarm.

Conditional probability table for Sophia Calls:

The Conditional probability of Sophia that she calls is depending on its Parent Node "Alarm."

From the formula of joint distribution, we can write the problem statement in the form of probability distribution:

P(S, D, A, ¬B, ¬E) = P (S|A) *P (D|A)*P (A|¬B ^ ¬E) *P (¬B) *P (¬E).

= 0.75* 0.91* 0.001* 0.998*0.999

= 0.00068045.

Hence, a Bayesian network can answer any query about the domain by using Joint distribution.

The semantics of Bayesian Network:

There are two ways to understand the semantics of the Bayesian network, which is given below:

1. To understand the network as the representation of the Joint probability distribution.

It is helpful to understand how to construct the network.

2. To understand the network as an encoding of a collection of conditional independence statements.

It is helpful in designing inference procedure.

References:

1. Stuart Russell, Peter Norvig, “Artificial Intelligence – A Modern Approach”, Pearson Education

2. Elaine Rich and Kevin Knight, “Artificial Intelligence”, McGraw-Hill

3. E Charniak and D McDermott, “Introduction to Artificial Intelligence”, Pearson Education

4. Dan W. Patterson, “Artificial Intelligence and Expert Systems”, Prentice Hall of India