Unit – 1
Set Theory, Functions and Natural Numbers
A collection of unique things of the same type or class of objects is referred to as a set. A set's goals are referred to as its elements or members. Numbers, alphabets, names, and other objects are examples of objects.
Sets- A set is a collection of well-defined objects which are called the elements or members of the set.
We generally use capital letters to denote sets and lowercase letters for elements.
If any element which exists in the set is to be denoted as-
Suppose an element ‘a’ is from a set X, then it is represented as- a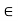
X
Which means the element ‘a’ belongs to the set X.
If the element is not form the group then we use ‘not belongs to’.
Examples of sets are:
- A set of rivers of India.
- A set of vowels.
A set is denoted by the capital letters A, B, C, and so on, whereas the basics of the set are denoted by the small letters a, b, x, y, and so on.
If A is a set and an is one of its elements, we refer to it as an a ∈ A. "Element of" is the meaning of the sign ∈ in this case.
Set Representation
There are two ways to express a set:
a) Roster or tabular form: We list all the components of the set within braces {} and separate them with commas in this type of representation.
For example, if A is a set of all odd numbers less than 10, then A= {1,3,5,7,9} can be written in the roster.
b) Set Builder form: In this representation, we list all of the qualities that all of the set's elements satisfy. We write as {x: x satisfies properties P}. and can be read as 'the set of all x such that each x has the attributes P.'
For example, If B= {2, 4, 8, 16, 32}, the set builder representation will be: B={x: x=2n, where n ∈ N and 1≤ n ≥5}.
Subsets-
Let every element of set X is also an element of a set Y, then X is said to be the subset of Y.
Symbolically it is written as-
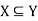
Which is read as- X is the subset of Y.
Note- If X = Y then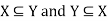 
Proper sub-set-
A set X is called proper subset the set Y is-
1. X is subset of Y
2. Y is not subset of X
Note- every set is a subset to itself.
Equal sets-
If X and Y are two sets such that every element of X is an element of Y and every element of Y is an element of X, the set and set Y will be equal always.
We write it as X = Y and read as X and Y are identical.
Super set-
If X is a subset of Y, then Y is called a super set of X.
Null set-
A set which does not contain any element is known as null set.
We denote a null set by ∅
The null set is a subset of every set.
Singleton-
A set which has only one element is called singleton.
Example- A = {10} and B = {∅}
Theorem- if ∅ and ∅’ are empty sets then ∅=∅’
Proof: Let ∅≠ ∅’ then the following conditions must be true-
1. There is element x∈∅ such that x∉∅’
2. There is element x∈∅’ such that x∉∅.
But both these conditions are false since ∅’ and ∅’ has any elements if follows that ∅=∅’.
Key takeaway
- A collection of unique things of the same type or class of objects is referred to as a set.
- A set's goals are referred to as its elements or members.
- Numbers, alphabets, names, and other objects are examples of objects.
A Venn diagram is a picture of a set in which the sets are represented by enclosed areas in the plane. The interior of a rectangle represents the universal set U, whereas disks within the rectangle represent the other sets. If A B, the disk representing A will be completely enclosed by the disk representing B, as seen in Figure (a). If A and B are disjoint, the disks representing A and B will be separated, as seen in Fig(b).
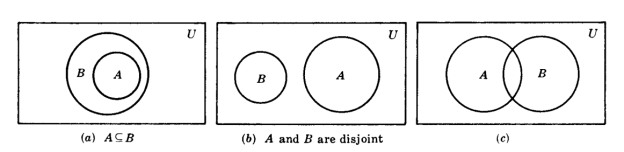
Fig 1: Venn diagram
However, if A and B are two arbitrary sets, some items may be in A but not in B, some in B but not in A, some in both A and B, and some in neither A nor B; so, in general, we express A and B as in Fig (c).
Union and Intersection
The set of all elements that belong to either A or B, denoted by A B, is the union of two sets A and B.
A ∪ B = {x | x ∈ A or x ∈ B}
The word "or" is used in this context to mean "and/or." A Venn diagram with A and B shading is shown in Figure (a).
The set of elements that belong to both A and B, indicated as A B, is the intersection of two sets A and B.
A ∩ B = {x | x ∈ A and x ∈ B}
A Venn diagram with A and B shading is shown in Figure (b).
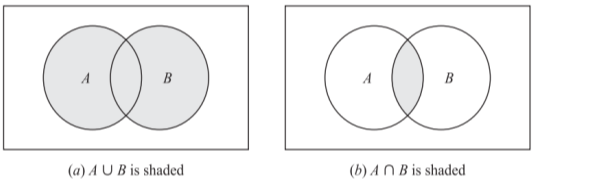
Fig 2: Union and intersection
Key takeaway
- A Venn diagram is a picture of a set in which the sets are represented by enclosed areas in the plane.
- The interior of a rectangle represents the universal set U, whereas disks within the rectangle represent the other sets.
A multiset is an unsorted collection of elements in which each element's multiplicity can be one, multiples of one, or zero. The multiplicity of an element refers to how many times it appears in the multiset. To put it another way, we can say that an element can appear in a set any number of times.
Example
A = {l, l, m, m, n, n, n, n}
B = {a, a, a, a, a, c}
Operation on multiset
- Union of multisets
The union of two multisets A and B is a multiset in which the multiplicity of an element equals the greatest multiplicity of an element in both A and B, and is represented by A ∪ B.
Example
Let A = {l, l, m, m, n, n, n, n}
B = {l, m, m, m, n},
A ∪ B = {l, l, m, m, m, n, n, n, n}
2. Intersection of multisets
A b is a multiset formed by the intersection of two multisets A and B, where the multiplicity of an element is equal to the minimum of the multiplicity of an element in both A ∩ B.
Example
Let A = {l, l, m, n, p, q, q, r}
B = {l, m, m, p, q, r, r, r, r}
A ∩ B = {l, m, p, q, r}.
3. Difference of multisets
The difference of two multisets A and B is a multiset whose multiplicity is equal to the multiplicity of the element in A minus the multiplicity of the element in B if the difference is positive, and is equal to 0 if the difference is negative or zero.
Example
Let A = {l, m, m, m, n, n, n, p, p, p}
B = {l, m, m, m, n, r, r, r}
A - B = {n, n, p, p, p}
4. Sum of multisets
The sum of two multisets A and B is a multiset in which an element's multiplicity equals the sum of its multiplicity in both A and B.
Example
Let A = {l, m, n, p, r}
B = {l, l, m, n, n, n, p, r, r}
A + B = {l, l, l, m, m, n, n, n, n, p, p, r, r, r}
5. Cardinality of sets
The cardinality of a multiset is the number of different elements in the set, ignoring the element's multiplicity.
Example
A = {l, l, m, m, n, n, n, p, p, p, p, q, q, q}
The multiset A has a cardinality of 5.
Key takeaway
- A multiset is an unsorted collection of elements in which each element's multiplicity can be one, multiples of one, or zero.
- The multiplicity of an element refers to how many times it appears in the multiset.
- To put it another way, we can say that an element can appear in a set any number of times.
An Ordered Pair is made up of two parts, one of which is identified as the first and the other as the second.
The ordered pairs (a, b) and (b, a) are distinct. In the case of an ordered pair, an ordered triple can be represented as (a, b) c.
An ordered Quadrable is an ordered pair with the first element as an ordered triple (((a, b), c) d).
An ordered n-tuple is an ordered pair with an ordered (n - 1) tuple as the first component and the nth element as the second component.
{(n -1), n}
Example
Ordered set of 5 elements
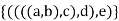
Example 1: Use set builder notation and logical equivalences to establish the first De Morgan law A ∩ B = A ∪ B.
Solution: We can prove this identity with the following steps
A ∩ B = {x | x /∈ A ∩ B} by definition of complement
= {x | ¬(x ∈ (A ∩ B))} by definition of does not belong symbol
= {x | ¬(x ∈ A ∧ x ∈ B)} by definition of intersection
= {x | ¬(x ∈ A) ∨ ¬(x ∈ B)} by the first De Morgan law for logical equivalences
= {x | x /∈ A ∨ x /∈ B} by definition of does not belong symbol
= {x | x ∈ A ∨ x ∈ B} by definition of complement
= {x | x ∈ A ∪ B} by definition of union
= A ∪ B by meaning of set builder notation
This proof employs the second De Morgan law for logical equivalences, in addition to the definitions of complement, union, set membership, and set builder notation.
Proving a set identity involving more than two sets by demonstrating that one side is a subset of the other sometimes necessitates keeping track of distinct circumstances.
Example 2: Let A, B, and C be sets. Show that A ∪ (B ∩ C) = (C ∪ B) ∩ A.
Solution: We have
A ∪ (B ∩ C) = A ∩ (B ∩ C) by the first De Morgan law
= A ∩ (B ∪ C) by the second De Morgan law
= (B ∪ C) ∩ A by the commutative law for intersections
= (C ∪ B) ∩ A by the commutative law for unions
Definition and Properties
Let P and Q be two sets that aren't empty. A subset of P x Q from a set P to Q is defined as a binary relation R. If (a, b) ∈ R and R ⊆ P x Q, then a and b are connected by R, i.e., aRb. When the sets P and Q are equivalent, we say R ⊆ P x P is a relation on P, for example
(i) Let A = {a, b, c}
B = {r, s, t}
Then R = {(a, r), (b, r), (b, t), (c, s)}
Is a relation from A to B.
(ii) Let A = {1, 2, 3} and B = A
R = {(1, 1), (2, 2), (3, 3)}
Is a relation (equal) on A.
Example - How many relations exist between A and A if a set has n elements?
Solution -
A x A has n2 items if the set A has n elements. As a result, there exist 2n2 relationships between A and A.
Domain of relation - The set of elements in P that are related to some elements in Q, or the set of all initial entries of the ordered pairs in R, is the domain of relation R. DOM is the abbreviation for it (R).
Range of relation - The scope of the relationship R is the set of all second entries of the ordered pairs in R, alternatively it is the set of all elements in Q that are connected to some element in P. RAN is the abbreviation for it (R).
Example: Let A = {1, 2, 3, 4}
B = {a, b, c, d}
R = {(1, a), (1, b), (1, c), (2, b), (2, c), (2, d)}.
Solution:
DOM (R) = {1, 2}
RAN (R) = {a, b, c, d}
Operation on relation
A subset of the Cartesian product of A and B is a binary relation between two nonempty sets A and B (in that order) (in that order). Because relations are sets, they can be affected by standard set operations. For example, given two relations R1 and R2, we can compute their union, intersection, and difference.
Union of two relations
Given two relations R1 and R2, the union of these relations, represented by R1 ∪ R2, will be defined as
R1 ∪ R2 ab R ab R = {(a, b) / (a, b) ∈ R1 ∨ (a, b) ∈ R2}
Intersection of two relations
Given two relations R1 and R2, we shall define R1 ∩ R2 as the intersection of these two relations.
R1 ∩ R2 = {(a, b) / (a, b) ∈ R1 ∧ (a, b) ∈ R2}
Difference of two relations
We will define the difference of relations R1 and R2 (in that order), represented by R1– R2, as follows:
R1 − R2 = {(a, b) / (a, b) ∈ R1 ∧ (a, b) ∉ R2}
Key takeaway
- The set of elements in P that are related to some elements in Q, or the set of all initial entries of the ordered pairs in R, is the domain of relation R.
- The scope of the relationship R is the set of all second entries of the ordered pairs in R.
- A subset of the Cartesian product of A and B is a binary relation between two nonempty sets A and B (in that order).
Let A, B, and C be sets, and let R be a relation from A to B and let S be a relation from B to C. That is, R is a subset of A × B and S is a subset of B × C. Then R and S give rise to a relation from A to C indicated by R◦S and defined by:
a (R◦S) c if for some b ∈ B we have aRb and bSc.
Is,
R ◦ S = {(a, c)| there exists b ∈ B for which (a, b) ∈ R and (b, c) ∈ S}
The relation R◦S is known the composition of R and S; it is sometimes denoted simply by RS.
Let R is a relation on a set A, that is, R is a relation from a set A to itself. Then R◦R, the composition of R with itself, is always represented. Also, R◦R is sometimes denoted by R2. Similarly, R3 = R2◦R = R◦R◦R, and so on. Thus Rn is defined for all positive n.
Example: Let X = {4, 5, 6}, Y = {a, b, c} and Z = {l, m, n}. Consider the relation R1 from X to Y and R2 from Y to Z.
R1 = {(4, a), (4, b), (5, c), (6, a), (6, c)}
R2 = {(a, l), (a, n), (b, l), (b, m), (c, l), (c, m), (c, n)}
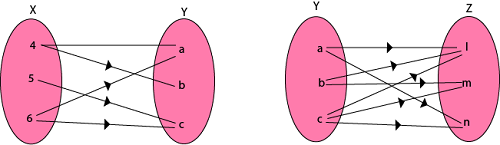
Fig 3: Example
Find the composition of relation (i) R1 o R2 (ii) R1o R1-1
Solution:
(i) The composition relation R1 o R2 as shown in fig:
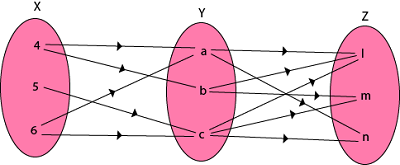
Fig 4: R1 o R2
R1 o R2 = {(4, l), (4, n), (4, m), (5, l), (5, m), (5, n), (6, l), (6, m), (6, n)}
(ii) The composition relation R1o R1-1 as shown in fig:
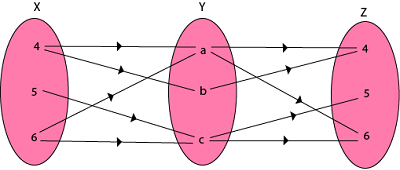
Fig 5: R1 o R-11
R1o R1-1 = {(4, 4), (5, 5), (5, 6), (6, 4), (6, 5), (4, 6), (6, 6)}
Key takeaway
- Let A, B, and C be sets, and let R be a relation from A to B and let S be a relation from B to C.
- That is, R is a subset of A × B and S is a subset of B × C.
If a relation R on a set A satisfies the following three criteria, it is termed an equivalence relation:
- Relation R is Reflexive, i.e., aRa ∀ a∈A.
- Relation R is Symmetric, i.e., aRb ⟹ bRa
- Relation R is transitive, i.e., aRb and bRc ⟹ aRc.
Example: Let A = {1, 2, 3, 4} and R = {(1, 1), (1, 3), (2, 2), (2, 4), (3, 1), (3, 3), (4, 2), (4, 4)}.
Demonstrate that R is a Relation of Equivalence.
Solution:
Reflexive: (1, 1), (2, 2), (3, 3) and (4, 4) ∈ R are all reflexive relationships.
Symmetric: Relation R is symmetric because whenever (a, b) ∈ R, (b, a) also belongs to R.
Example: (2, 4) ∈ R ⟹ (4, 2) ∈ R.
Transitive: R is transitive because anytime (a, b) and (b, c) are members of R, (a, c) is also a member of R.
Example: (3, 1) ∈ R and (1, 3) ∈ R ⟹ (3, 3) ∈ R
R is an Equivalence Relation since it is reflexive, symmetric, and transitive.
A relation R on a set A is reflexive if aRa for every a ∈ A, that is, if (a, a) ∈ R for every a ∈ A. Thus, R is not reflexive if there exists a ∈ A such that (a, a) ∈/ R.
Example: Consider the following five relations on the set A = {1, 2, 3, 4}:
R1 = {(1, 1), (1, 2), (2, 3), (1, 3), (4, 4)}
R2 = {(1, 1) (1, 2), (2, 1), (2, 2), (3, 3), (4, 4)}
R3 = {(1, 3), (2, 1)}
R4 = ∅, the empty relation
R5 = A × A, the universal relation.
Determine which of the relationships is reflexive.
Because A contains the four elements 1, 2, 3, and 4, any relation R on A that contains the four pairings (1, 1), (2, 2), (3, 3), and (4, 4) is reflexive (4, 4). R2 and the universal relation R5 = A × A are hence the sole reflexive functions. R1, R3, and R4 are not reflexive, because (2, 2), for example, does not belong to any of them.
If a relation R on a set A has the following three criteria, it is termed a partial order relation:
- Relation R is Reflexive, i.e., aRa ∀ a∈A.
- Relation R is Antisymmetric, i.e., aRb and bRa ⟹ a = b.
- Relation R is transitive, i.e., aRb and bRc ⟹ aRc.
Example: Show that the relation (x, y) ∈ R is a partial order relation if x ≥ y are specified on the set of +ve integers.
Solution: Consider the four +ve integers in the set A = 1, 2, 3, 4. Determine a relationship for this collection, such as R = {(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3), (1, 1), (2, 2), (3, 3), (4, 4)}.
Reflexive - The relation is reflexive as for every a ∈ A. (a, a) ∈ R, i.e. (1, 1), (2, 2), (3, 3), (4, 4) ∈ R.
Antisymmetric - The relationship is antisymmetric since a = b whenever (a, b) and (b, a) ∈ R.
Transitive - Because we have (a, b) and (b, c) ∈ R whenever, we have (a, c) ∈ R.
Example - (4, 2) ∈ R and (2, 1) ∈ R, implies (4, 1) ∈ R.
Because the relationship is reflexive, anti symmetrical, and transitive, it is reflexive, anti symmetrical, and transitive. As a result, it's a partial order relationship.
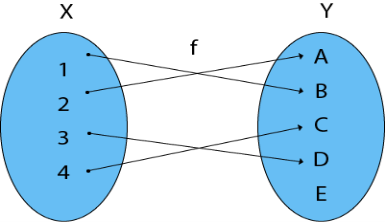
It's a mapping in which each element in set A is linked to a specific element in set B. The domain of a function is the set of A, and the domain of B is the set of B.
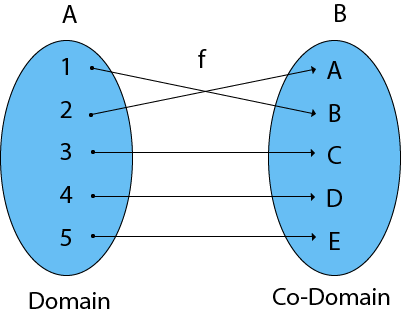
Fig 6: Domain and co-domain
Domain, Co-domain, and Range of function
Domain - Let f be a function that goes from point P to point Q. The domain of the function f is the set P.
Co-domain - Let f be a function that goes from point P to point Q. The set Q is referred to as the function f's Co-domain.
Range - The collection of pictures in a function's domain is its range. To put it another way, it is a subset of its co-domain. The letter f is used to represent it (domain).
If f: P → Q, then f (P) = {f(x): x ∈ P} = {y: y ∈ Q | ∃ x ∈ P, such that f (x) = y}.
Example: Find the function's Domain, Co-Domain, and Range.
Let x = {1, 2, 3, 4}
y = {a, b, c, d, e}
f = {(1, b), (2, a), (3, d), (4, c)
Solution: Domain of function: {1, 2, 3, 4}
Range of function: {a, b, c, d}
Co-Domain of function: {a, b, c, d, e}
Classification of functions
- Injective (One-to-One) Functions: One element of the Domain Set is associated to one element of the Co-Domain Set in this function.
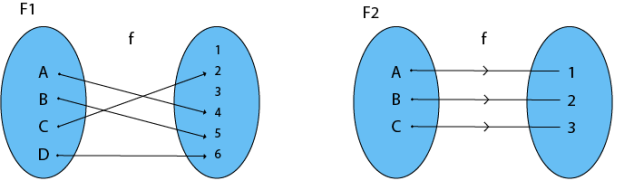
Fig 7: f1 and f2 show one to one function
2. Surjective (Onto) Functions: Every element of the Co-Domain Set has one pre-image in this function.
Example: Consider, A = {1, 2, 3, 4}, B = {a, b, c} and f = {(1, b), (2, a), (3, c), (4, c)}.
Because every element of B is the image of some A, it is a Surjective Function.
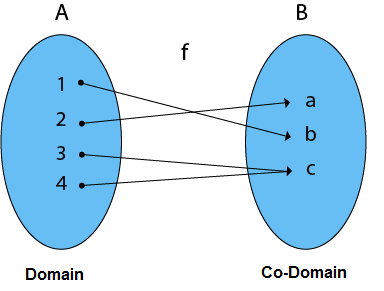
Fig 8: Surjective function
3. Bijective (One-to-One Onto) Functions: Bijective (One-to-One Onto) Function is a function that is both injective (one to one) and surjective (onto).
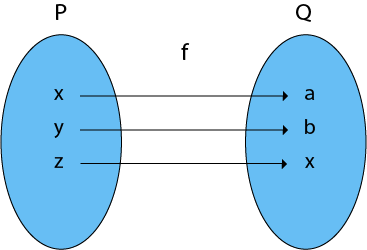
Fig 9: One to one function
Example: Consider P = {x, y, z}
Q = {a, b, c}
And f: P → Q such that
f = {(x, a), (y, b), (z, c)}
The f is both a one-to-one and an onto function. It is, thus, a bijective function.
4. Into Functions: There is no pre-image in domain X for a function that requires an element from co-domain Y.
Example: Consider, A = {a, b, c}
B = {1, 2, 3, 4} and f: A → B such that
f = {(a, 1), (b, 2), (c, 3)}
In the function f, the range i.e., {1, 2, 3} ≠ co-domain of Y i.e., {1, 2, 3, 4}
As a result, it is an into function.
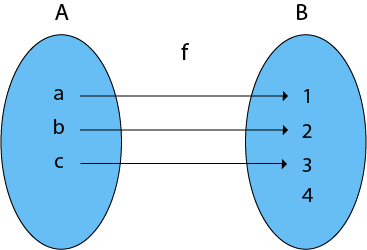
Fig 10: Into function
5. One-One Into Functions: Let f: X →Y be the case. If distinct elements of X have different unique images of Y, the function f is called one-one into function.
Example: Consider, X = {k, l, m}
Y = {1, 2, 3, 4} and f: X → Y such that
f = {(k, 1), (l, 3), (m, 4)}
The function f is a one-to-one conversion.
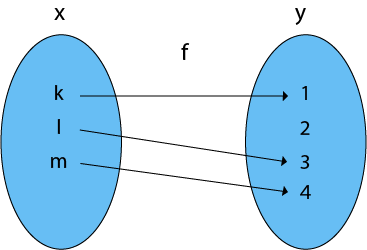
Fig 11: One one into function
6. Many-One Functions: Let f: X →Y be the case. If there are two or more separate items in X that have the same image in Y, the function f is said to be a many-one function.
Example: Consider X = {1, 2, 3, 4, 5}
Y = {x, y, z} and f: X → Y such that
f = {(1, x), (2, x), (3, x), (4, y), (5, z)}
The function f is a many to one
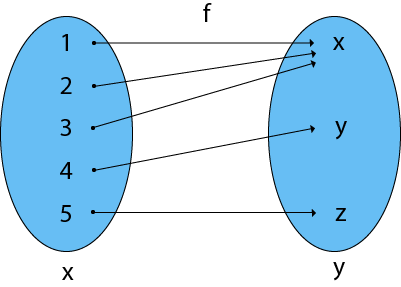
Fig 12: Many to one function
7. Many-One Into Functions: Let f: X→Y be the case. If and only if is both many one and into function, the function f is termed the many-one function.
Example: Consider X = {a, b, c}
Y = {1, 2} and f: X → Y such that
f = {(a, 1), (b, 1), (c, 1)}
Because f is a many-one and into function, it is also a many-one into function.
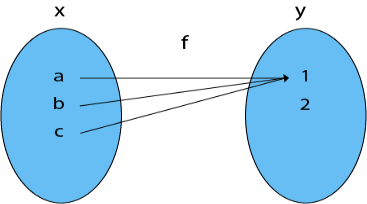
Fig 13: Many one into function
8. Many-One Onto Functions: Let f: X→ Y be the case. If and only if is both many one and onto, the function f is termed a many-one onto function.
Example: Consider X = {1, 2, 3, 4}
Y = {k, l} and f: X → Y such that
f = {(1, k), (2, k), (3, l), (4, l)}
The function f is a many-one (since the two elements in Y have the same image) and onto (as every element of Y is the image of some element X). As a result, it is a many-to-one function.
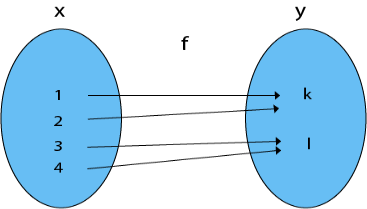
Fig 14: Many one onto function
Key takeaway
- It's a mapping in which each element in set A is linked to a specific element in set B.
- The domain of a function is the set of A, and the domain of B is the set of B.
If the function definition refers to itself, it is considered to be recursively defined. The function definition must contain the following two properties in order to avoid being circular:
(1) The function must not refer to itself for specific parameters, referred to as base values.
(2) The function's argument must be closer to a base value each time the function refers to itself.
The term "well-defined" refers to a recursive function that has these two features.
The examples that follow should assist to understand these concepts.
Factorial Function
The product of positive numbers from 1 to n, inclusive, is known as "n factorial" and is generally written as n! That is to say,
n! = n (n − 1) (n − 2) ··· 3 · 2 · 1
It's also handy to specify 0! = 1 to ensure that the function works for all nonnegative numbers. Thus:
0! = 1, 1! = 1, 2! = 2 · 1 = 2, 3! = 3 · 2 · 1 = 6, 4! = 4 · 3 · 2 · 1 = 24 5! = 5 · 4 · 3 · 2 · 1 = 120, 6! = 6 · 5 · 4 · 3 · 2 · 1 = 720
And so forth. Take note of this:
5! = 5 · 4! = 5 · 24 = 120 and 6! = 6 · 5! = 6 · 120 = 720
This holds for any positive integer n; in other words,
n! = n · (n − 1)!
As a result, the factorial function can be written as follows.
Factorial function: (a) If n = 0, then n! = 1.
(b) If n > 0, then n! = n · (n − 1)!
It's worth noting that the previous definition of n! is recursive, as it uses (n 1)! to refer to itself. However:
(1) When n = 0, the value of n! is explicitly stated (thus 0 is a base value).
(2) For each random n, the value of n! is defined in terms of a smaller n that is closer to the base value 0.
Key takeaway
- If the function definition refers to itself, it is considered to be recursively defined.
- The function definition must contain the following two properties in order to avoid being circular.
The highest order term determines the rate of expansion of a function: if you add a bunch of terms, the function expands about as quickly as the largest term (for large enough input values).
The big-O notation is commonly used to describe the expansion of functions.
Let f and g be functions from integers or real numbers to real numbers, respectively.
If there are constants C and k such that |f(x)|≤ C|g(x)| whenever x > k, we say f(x) is O(g(x)).
f(x) and g(x) are always positive when we look at the evolution of complexity functions. As a result, we can reduce the big-O requirement to f(x) ≤ C.
When x > k, use g(x).
We simply need to identify one pair (C, k) to demonstrate that f(x) is O(g(x) (which is never unique).
The big-O notation is used to define an upper limit for the growth of a function f(x) for large x.
This border is defined by the g(x) function, which is typically much simpler than f. (x).
Because C does not grow with x, we accept the constant C in the criterion f(x) ≤ C.g(x) whenever x > k.
We only care about large x, thus it's fine if f(x) > C.g(x) for x ≤ k.
Example
Show that f(x) = x2 + 2x + 1 is O(x2).
For x > 1 we have:
x2 + 2x + 1 ≤ x2 + 2x2 + x2
x2 + 2x + 1 4x2
Therefore, for C = 4 and k = 1:
f(x) ≤ Cx2 whenever x > k.
f(x) is O(x2).
Key takeaway
The highest order term determines the rate of expansion of a function: if you add a bunch of terms, the function expands about as quickly as the largest term (for large enough input values).
The nonnegative integers, N=0, 1, 2, 3..., are the natural numbers. Create definitions for the following integer relations using the concept of natural numbers: less than (), less than or equal to (), greater than (>), and greater than or equal to ().
Note that several authors define natural numbers as only positive integers; zero is not a natural number for them. This appears unnatural to me. The terms positive integers and nonnegative integers are unmistakable and well-understood among mathematicians. However, the term "natural number" is not completely standardized.
Set of natural numbers
A collection of elements is referred to as a set (numbers in this context). In mathematics, the set of natural numbers is written as 1,2,3, ... The set of natural numbers is symbolized by the symbol N. N = 1,2,3,4,5,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
Statement Form | N = Set of all numbers starting from 1. |
Roaster Form | N = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ………………………………} |
Set Builder Form | N = {x : x is an integer starting from 1} |
Smallest natural number
1 is the smallest natural number. We know that the smallest element in N is 1 and that we can talk about the next element in terms of 1 and N for any element in N. (which is 1 more than that element). Two is one greater than one, three is one greater than two, and so on.
Natural number from 1 to 100
The natural numbers from 1 to 100 are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99 and 100.
Key takeaway
- The nonnegative integers, N=0, 1, 2, 3..., are the natural numbers.
- Create definitions for the following integer relations using the concept of natural numbers: less than (), less than or equal to (), greater than (>), and greater than or equal to ().
- In mathematics, the set of natural numbers is written as 1,2,3, ... The set of natural numbers is symbolized by the symbol N. N = 1,2,3,4,5,,,,,,,,,
Mathematical induction is a mathematical technique is used to prove a statement, a theorem or a formula is true for every natural number.
The technique has two steps to prove any statement-
1. Base step (it proves that a statement is true for the initial value)
2. Inductive step (it proves that is the statement is true for n’th iteration then it is also true for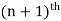 
iteration.
Example-1: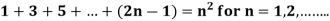 
Sol. Here for n = 1, 1 = 1²
Now let us assume that the statement is true for n = k
Hence, we assume that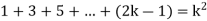 
is true.
Now we need to prove that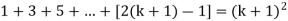
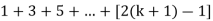
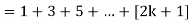
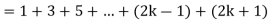
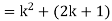
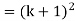
So that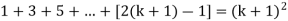 
which satisfies the second step.
Hence-
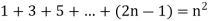
Example-2: Prove 1+2+...+n = n(n+1)/2 using a proof by induction
Sol.
Let n=1: 1 = 1(1+1)/2 = 1(2)/2 = 1 is true,
Step-1: Assume n=k holds: 1+2+...+k = k(k+1)/2
Show n=k+1 holds: 1+2+...+k+(k+1) =(k+1) ((k+1) +1)/2
Substitute k with k+1 in the formula to get these lines. Notice that I write out what I want to prove.
Step-2: Now start with the left side of the equation
1+2+...+(k+1) =1+2+...+k+(k+1)
=k(k+1)/2 + (k+1)
=(k(k+1)+2(k+1))/2 by 2/2=1 and distridution of division over addition
=(k+2)(k+1)/2 by distribution of multiplication over addition
=(k+1)(k+2)/2 by commutativity of multiplication
Example-3: Prove the following by using the principle of mathematical induction for all n ∈ N-
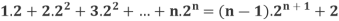
Sol. Here, n = 1,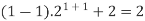 
, which is true
Step-1: Assume n = k holds-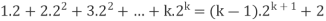 
Now show n = k + 1 also holds-
Consider-
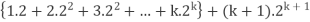
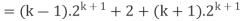
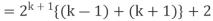
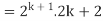
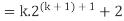
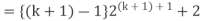
Which is also true for n = k + 1
Hence proved.
Strong induction
Another type of mathematical induction is strong induction. We can use the following procedures to prove that a propositional function, P(n), is true for all positive integers, n, using this induction technique:
Step 1(Base step) - It establishes the truth of the original statement P (1).
Step 2 (Inductive step) - It proves that the conditional statement
[P(1)∧P(2)∧P(3)∧⋯∧P(k)]→P(k+1) is true for positive integers k.
Prove the following by Mathematical Induction:
1 + 3 + 5 +.... + 2n - 1 = n2.
Solution: let us assume that.
P (n) = 1 + 3 + 5 +..... + 2n - 1 = n2.
For n = 1, P (1) = 1 = 12 = 1
It is true for n = 1................ (i)
Induction Step: For n = r,
P (r) = 1 + 3 + 5 +..... +2r-1 = r2 is true......................... (ii)
Adding 2r + 1 in both sides
P (r + 1) = 1 + 3 + 5 +...... +2r-1 + 2r +1
= r2 + (2r + 1) = r2 + 2r +1 = (r+1)2..................... (iii)
As P(r) is true. Hence P (r+1) is also true.
From (i), (ii) and (iii) we conclude that.
1 + 3 + 5 +...... + 2n - 1 =n2 is true for n = 1, 2, 3, 4, 5 ....
Hence Proved.
A mathematical proof is a logical argument used to support a mathematical proposition. We evaluate two elements while validating a statement: the statement and the logical operators.
Proof by cases
A statement can be true or untrue, but not both at the same time. AND, OR, NOT, If then, and If and only if are logical operators. They exist when combined with quantifiers like for all. To ensure that the assertion is correct, we apply operators to it.
This method involves evaluating each scenario of the statement to determine its truthfulness.
Example: The integer x(x + 1) is even for every integer x.
Proof: If x is an even number, then x = 2k for some k. The statement now reads:
2k (2k + 1)
It is even because it is divisible by two.
If x is odd, the sentence becomes: x = 2k + 1 for some number k.
(2k+1) (2k+1+1) = (2k + 1) 2(k + 1)
We established that x(x+1) is even in both circumstances since it is divisible by 2.
Proof by induction
The Mathematical Induction Principle (PMI). P(n) represents a statement about the positive integer n. If the following statements are correct:
1. P (1),
2. (for all n there exists Z+) P(n) implies P (n + 1),
Then (for all n there exists Z+) P(n).
For each positive integer n, consider the following example.
1 + 2 +···+ n = n (n + 1)/ 2
Proof: If n = 1, this is the base case.
1 + ··· + n = 1
And
n (n + 1)/2 = 11
Inductive step: Assume that there is a Z+ for a given n.
1 + 2 +···+ n = n (n + 1)/ 2 ---- (i) (inductive hypothesis)
Our purpose is to demonstrate that:
1 + 2 +···+ n + (n + 1) = [n + 1] ([n + 1] + 1)/ 2
i.e., 1 + 2 +···+ n + (n + 1) = (n + 1) (n + 2) /2
When both sides of equation I are multiplied by n+1, we get
1 + 2 +···+ n + (n + 1)
= n (n + 1)/ 2 + (n + 1)
= n (n + 1) /2 + 2(n + 1) /2
= (n + 2) (n + 1) /2
In logic and mathematics, proof by contradiction is a method of determining the truth of a statement by assuming it is false, then trying to show it is incorrect until the conclusion of that assumption is a contradiction.
Proof by contradiction: Steps
Let's break it down into steps to better understand how proof by contradiction works. When employing evidence by contradiction, we follow these steps:
● Assume that your statement is incorrect.
● Proceed as if you were working on a direct proof.
● You've come across an inconsistency.
● Declare that, because of the contradiction, the statement cannot be wrong, hence it must be true.
Example
Do you recall what I said earlier?
No integers y and z exist for which
24y + 12z = 1
You may spend days, weeks, or even years wandering around with precise numbers to demonstrate that any integer you try in the sentence works.
For example, try y = -5, and z = 7.
24 x -5 + 12 x 7 = 1
-120 + 84 = - 36
Those integers didn't work, so how about repeating it again with a few hundred more integers for a few hours? Most likely not. However, we can try to disprove the statement by using evidence by contradiction:
No integers a and b exist for which
24y + 12z = 1
To show that this is wrong, we assume that we can find numbers y and z to solve the equation:
24y + 12z = 1 the original equation
By multiplying both sides by 12, the biggest common factor emerges.
2y + z = 1/12
The effect caused by dividing both sides by the greatest common factor of the two integers strikes us right away. The total number of integers is a fraction!
Key takeaway
- In logic and mathematics, proof by contradiction is a method of determining the truth of a statement by assuming it is false, then trying to show it is incorrect until the conclusion of that assumption is a contradiction.
References:
1. Koshy, Discrete Structures, Elsevier Pub. 2008 Kenneth H. Rosen, Discrete Mathematics and Its Applications, 6/e, McGraw-Hill, 2006.
2. B. Kolman, R.C. Busby, and S.C. Ross, Discrete Mathematical Structures, 5/e, Prentice Hall, 2004.
3. E.R. Scheinerman, Mathematics: A Discrete Introduction, Brooks/Cole, 2000.
4. R.P. Grimaldi, Discrete and Combinatorial Mathematics, 5/e, Addison Wesley, 2004
5. Liptschutz, Seymour, “Discrete Mathematics”, McGraw Hill.
