Unit - 2

Algebraic Structures

2.1 Definition

An algebraic structure is a non-empty set G that contains one or more binary operations. Let's pretend that * is a binary operation on G. The structure (G, *) is then algebraic. The algebraic structure is represented by (N,*), (1, +), and (1, -). (R, +,.) is an algebraic structure with two operations in this case.

Example:

1. Let R be the set of real numbers, then (R, +) is an algebraic structure.
2. If N denotes the set of natural numbers then (N, +) is an algebraic structure.

Binary operation

A binary operation * in a set A is a function from A × A to A.

If * is a binary operation in a Set A then than for the * image of the ordered pair (a, b) 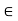A × A, we write a * b (or * (a, b)).

Note-

1. Addition (+) is a binary operation in the set of natural number N. Set of integers Z and set of real numbers R.

2. Multiplication (×) is a binary operation in N, Z, Q, R and C.

Property of algebraic structure

A property of an algebraic structure is one that any of its operations possesses. The following are some of the most important properties of an algebraic system:

1. Associative and commutative laws

If any of the members a, b, c in S meet the associative law, then an operation * on the set is said to be associative or to satisfy the associative law (a * b) * c = a * (b * c).

Note- The operations of addition and multiplication over the natural numbers are associative.

If a * b = b * a for any element a, b in S, the operation * is said to be commutative or meet the commutative law.

Note- Addition is commutative in the set of natural numbers.

2. Identity element and inverse

Consider the following operation * on the set S. If any element an in S - a * e = e * a = a, an element e in S is called an identity element.

Note- Zero is the identity element in the set integers with respect to the binary operation addition (i.e., +).

A left identity or a right identity for an element e is defined as e *a or a * e = a, where an is any element in S.

Let's pretend that an operation * on a set S has an identity element e. An element b is the inverse of an element in S, such that a * b = b * a = e.

3. Cancellation laws

A binary operation denoted by * in a set A, is said to satisfy

1. Left cancellation law if for all a, b, c 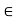A,

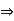a * b = a * c b = c

2.     Right cancellation law if for all a, b, c 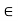A

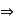b * a = c * a b = c

For example:

In P (A), the power set of A, union is distributive over intersection and intersection is distributive of union of sets.

Theorem: If * is an associative binary operation in a set A, such every element is invertible, then * satisfies the left as well as the right cancellation laws, which means

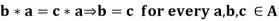
Proof:

Suppose e be the identity element of A with respect to *

Every element in A is invertible 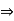a 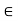A is invertible.

Let a’ denotes the inverse of a in A then

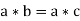
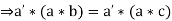
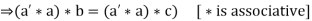
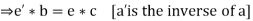
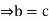
Similarly, it can be proved that

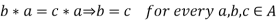
Key takeaway

1. An algebraic structure is a non-empty set G that contains one or more binary operations.
2. A property of an algebraic structure is one that any of its operations possesses.

2.2 Groups

A group is an algebraic structure (G, *) in which the binary operation * on G satisfies the following conditions:

Condition-1:  For all a, b, c, ∈G

a* (b * c) = (a * b) * c (associativity)

Condition-2: There exists an elements e ∈G such that for any a ∈G

a* e= e * a = a (existence of identity)

Condition-3: For every a ∈G, there exists an element denoted by 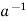in G such that

a* 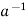= 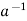* a = e

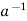is called the inverse of a in G.

Example: (Z, +) is a group where Z denote the set of integers.

Example: (R, +) is a group where R denote the set of real numbers.

Abelian group-

Let (G, *) be a group. If * is commutative that is

a* b = b * a for all a, b ∈G then (G, *) is called an Abelian group.

Finite group-

A group G is said to be a finite group if the set G is a finite set.

Infinite group-

A group G, which is not finite is called an infinite group.

Order of a finite group-

The order of a finite group (G, *) is the number of distinct elements in G. The order of

G is denoted by O (G) or by |G|.

Example: If G = {1, -1, i, -i} where i= 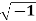, then show that G is an abelian group with respect to multiplication as a binary operation.

Sol.

First, we will construct a composition table-

It is clear from the above table that algebraic structure (G,.) is closed and satisfies the following conditions.

Associativity- For any three elements a, b, c ∈G (a ⋅b) ⋅c = a⋅(b ⋅c)

Since

1⋅(−1 ⋅i) = 1 ⋅−i= −i

(1 ⋅−1) ⋅i= −1 ⋅i= −i

⇒1⋅(−1 ⋅i) = (1 ⋅−1) i

Similarly with any other three elements of G the properties hold.

∴Associative law holds in (G, ⋅)

Existence of identity: 1 is the identity element (G, ⋅) such that 1 ⋅a = a = a ⋅1 ∀a ∈G

Existence of inverse: 1 ⋅1 = 1 = 1 ⋅1 ⇒1 is inverse of 1

(−1)⋅(−1) = 1 = (−1) ⋅(−1) ⇒–1 is the inverse of (–1)

i⋅(−i) = 1 = −i⋅i⇒–iis the inverse of iin G.

−i⋅i= 1 = i⋅(−i) ⇒iis the inverse of –iin G.

Hence inverse of every element in G exists.

Thus, all the axioms of a group are satisfied.

Commutativity: a ⋅b = b ⋅a ∀a, b ∈G hold in G

1 ⋅1 = 1 = 1 ⋅1, −1 ⋅1 = −1 = 1 ⋅−1

i⋅1 = i= 1 ⋅i; i⋅−i= −i⋅i= 1 = 1 etc.

Commutative law is satisfied

Hence (G, ⋅) is an abelian group.

Example-

Prove that the set Z of all integers with binary operation * defined by a * b = a + b + 1 ∀a, b ∈G is an abelian group.

Sol: Sum of two integers is again an integer; therefore a +b ∈Z ∀a, b ∈Z

⇒a +b + 1 ⋅∈Z ∀a, b ∈Z

⇒Z is called with respect to *

Associative law for all a, b, a, b ∈G we have (a * b) * c = a * (b * c) as

(a* b) * c = (a + b + 1) * c

= a + b + 1 + c + 1

= a + b + c + 2

Also

a* (b * c) = a * (b + c + 1)

= a + b + c + 1 + 1

= a + b + c + 2

Hence (a * b) * c = a * (b * c) ∈a, b ∈Z.

Groupoid-

Groupoid is an algebraic structure consisting of non-empty set A and a binary operation *, which is such that A is closed under *.

For example- The set of real numbers is closed under addition, therefore (R, +) is a groupoid.

Theorem:

Statement 1- There is just one identification element in a Group G. (uniqueness of identity) Proof: - In G, let e and e' be two distinct identities, and let a ∈ G

∴ ae = a ⟶(i)

∴ ae' = a ⟶(ii)

R.H.S of (i) and (ii) are equal ⇒ae =ae'

As a result of the left cancellation law, we get e=e'.

For any G, there is only one identity element. As a result, the theorem is established.

Statement 2 - There is a unique element b in G for each element an in a group G, such that ab= ba=e (uniqueness if inverses)

Proof: Assume that b and c are the inverses of an a ∈ G.

Then ab = e and ac = e

∵ c = ce {existence of identity element}

⟹ c = c (ab) {∵ ab = e}

⟹ c = (c a) b

⟹ c = (ac) b {∵ ac = ca}

⟹ c = eb

⟹ c = b {∵ b = eb}

As a result, the inverse of a G is unique.

Key takeaway

1. A monoid having an inverse element is referred to as a group.
2. The order of a group G is equal to the number of members in G, and the order of an element in a group is equal to the least positive integer n such that an is the group G's identity element.

2.3 Subgroups and order

Let (G, *) be a group and H, be a non-empty subset of G. If (H, *) is itself is a group, then (H, *) is called sub-group of (G, *).

Example-Let a = {1, –1, i, –i} and H = {1, –1}

G and H are groups with respect to the binary operation, multiplication.

H is a subset of G, therefore (H, X) is a sub-group (G, X).

Theorem-

If (G, *) is a group and H ≤G, then (H, *) is a sub-group of (G, *) if and only if

(i) a, b ∈H ⇒a * b ∈H;

(ii) a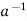∈H ⇒∈H

Proof:

If (H, *) is a sub-group of (G, *), then both the conditions are obviously satisfied.

We, therefore prove now that if conditions (i) and (ii) are satisfied then (H, *) is a sub-group of (G, *).

To prove that (H, *) is a sub-group of (G, *) all that we are required to prove is : * is associative in

H and identity e ∈H.

That * is associative in H follows from the fact that * is associative in G.

Also,

a∈H ⇒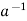∈H by (ii) and e ∈H and 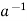∈H ⇒a * 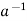= e ∈H by (i)

Hence, H is a sub-group of G.

Cyclic subgroup

A cyclic subgroup K of a group G exists if an element x ∈ G exists such that every element of K can be expressed in the form xn for some n ∈Z.

The element x is referred to as the K generator, and we write K= <x>.

Order

The number of components in the group G determines its order. |G| is the symbol for it. Only the identity element, (e *), is present in an order 1 group.

A group of order 2 consists of two members, one of which is the identity element and the other of which is some other element.

Definition (order of an element)

Let (G, *) be a group and a 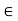G, then the least positive integers, n if it exists such that an = e is called the order of a 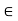G.

The order of an element a 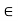G is be denoted by O (a).

Note-

The order of every element of a finite group is finite.

The order of an element of a group is always equal to the order of its inverse.

The order of any integral power of any element of an group is less then or equal to the order of the element.

Example 1: Consider the order 2 group (e, x, *). The operation table is displayed.

Three items make up the order 3 group: one identity element and two other elements.

Key takeaway

1. H is a subgroup of G if a non-void subset H of a group G is itself a group under the operation of G.
2. The number of components in the group G determines its order. |G| is the symbol for it.
3. Only the identity element, (e *), is present in an order 1 group.

2.4 Cyclic Groups

A cyclic group is one that can be made up of only one element. Every member of a cyclic group is a power of a generator, which is a specific element. A generator 'g' can create a cyclic group in which every other element of the group can be represented as a power of the generator 'g'.

When G=, we say that G is cyclic and that x is a generator of G. That is, if there is an element x ∈ G such that every element of G can be written in the form xn for any n ∈ Z, the group G is said to be cyclic.

Under ordinary multiplication, the group G=1, -1, i, -i is a finite cyclic group with I as generator, thus i1=i, i2=-1, i3=-i and i4=1

Although every cyclic group is an abelian group, not every abelian group is cyclic. The rational numbers under addition are abelian, not cyclic.

Example: Let Z denote the set of integers (Z, +) is an infinite cyclic group 1 and –1 are the generators of the group (Z, +).

Abelian group

Consider the algebraic system (G,*), in which * represents a binary operation on G. The system (G, *) is therefore considered to be an abelian group if it satisfies all of the group's properties plus the following property:

(1) The operation * is commutative i.e.,

a * b = b * a ∀ a, b ∈G

Example - Consider the algebraic system (G, *), in which G represents the set of all non-zero real numbers and * represents a binary operation defined by

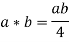
Demonstrate that the group (G, *) is an abelian one.

Solution:

Closure property - Because a * b 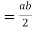Subgroup is a real number, the set G is closed by the operation *. As a result, it belongs to G.

Associative property - * is an associative operation. If we use a, b, c∈G, we get

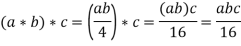
Similarly,

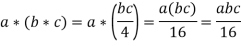
Identity - Assume that e is a +ve real number to get the identity element. Then e * a = a, with a being G.

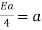        or          

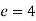
Similarly,

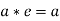
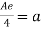  or  

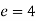
As a result, G's identification element is 4.

Inverse - Let's pretend that a ∈G. If the inverse of an is a-1∈Q, then a * a-1=4.

Therefore 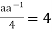  or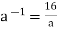 

Similarly,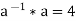

Therefore, 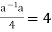  or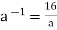

As a result, in G, the inverse of element an is .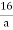

Commutative - * on G is a commutative operation.

Since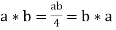

G, * is thus a closed, associative, identity element, inverse, and commutative algebraic system. As a result, the system (G, *) belongs to the abelian group.

Theorem: Every cyclic group is abelian

Proof:

Suppose (G, *) be a cyclic group

Generated by a

x, y 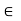G

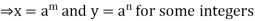
m and n

x * y = *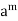

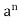
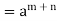
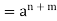
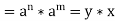
Theorem- Every group of prime order is cyclic.

Proof:

Let O (G) = p where p is a prime number and

Suppose

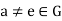
Consider the sub-group of G, generated by a

Let H = <a>

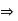O (H) > 1

H is a sub-group of G

By Lagrange’s theorem

O (H) / O (G) 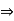O (H) / p

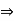O (H) = 1 or p

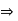O (H) = p since O (H)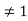

O (H) = O (G)

But H is cyclic 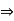G is cyclic

Note- Every proper sub-group of an infinite cyclic group is isomorphic to the group itself.

Every proper sub-group of finite cyclic group is a finite cyclic group.

The only groups which do not possess proper sub-group are the prime order finite sub-groups.

Key takeaway

1. A cyclic group is one that can be made up of only one element.
2. Every member of a cyclic group is a power of a generator, which is a specific element.

2.5 Cosets

Assume that H is a subgroup of G. For each x G, a left coset of H in G is a subset of G whose elements may be represented as xH= {xh | h ∈ H}. A representation of the coset is the element x. Similarly, for any x∈ G, a right coset of H in G is a subset that can be represented as Hx= {hx | h∈ H}. As a result, the complexes xH and Hx are referred to as a left coset and a right coset, respectively.

A left coset is denoted by x + H= {x+h | h ∈ H} if the group operation is additive (+), while a right coset is denoted by H + x = {h+x | h ∈ H} if the group operation is subtractive (-).

If G is a finite group, H is a subgroup of G, and g is an element of G, then in group theory;

The left coset of H in G with regard to the element of G is gH = gh: h an element of H.

And

The right coset of H in G with regard to the element of G is Hg = hg: h an element of H.

Theorem: If (H, *) is a sub-group (G, *), then a * H = H if and only if a ∈H.

Proof: Let a * H = H

Since e ∈H then a = a * e ∈a * H

Hence a ∈H

Conversely

Let a ∈H then a * H ⊆H

(H, *) is a sub-group.

∴a∈H, h ∈H ⇒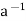* h ∈H.

Now h ∈H

⇒h = a * (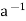 * h) ∈a * H

∴h∈H ⇒h ∈a * H

⇒H ⊆a * H

Hence a * H = H

Let us now consider the lemmas that aid in the proof of the Lagrange theorem.

Lemma 1: If G is a group with a subgroup H, then H and any coset of H have a one-to-one relationship.

Lemma 2: If G is a group with subgroup H, then the left coset relation, g1∼g2, is an equivalence relation if and only if g1 ∗ H = g2 ∗ H.

Let S be a set and be an equivalence relation on S. Lemma 3: Let S be a set and be an equivalence relation on S. If A and B are two equivalence classes, then A ∩ B =∅,

A = B.

Key takeaway

1. Assume that H is a subgroup of G.
2. For each x G, a left coset of H in G is a subset of G whose elements may be represented as xH= {xh | h ∈ H}.
3. A representation of the coset is the element x.
4. Similarly, for any x∈ G, a right coset of H in G is a subset that can be represented as Hx= {hx | h∈ H}.

2.6 Lagrange's theorem

One of the most important theorems in abstract algebra is the Lagrange theorem. It asserts that in group theory, the order of subgroup H of group G splits the order of G for any finite group G. The number of elements is represented by the group's order. Joseph-Louis Lagrange proved this theorem. Let us look at the statement and proof of the Lagrange theorem in Group theory, as well as the three lemmas that were utilized to prove this theorem with examples.

Lagrange Theorem Statement

The order of the subgroup H separates the order of the group G, according to the assertion. This can be written as:

|G| = |H|

The important terminologies and three lemmas that aid in the proof of the Lagrange theorem must be understood before proceeding with the proof.

Lagrange Theorem Proof

We may simply prove the Lagrange statement using the three lemmas presented before.

Proof of Lagrange Statement:

Let H be any subgroup of a finite group G of order m of order n. Take a look at G's cost breakdown in relation to H.

Let us now imagine that each coset of aH consists of n distinct items.

Let H = {h1, h2…,hn}, then ah1, ah2,…,ahn are the n distinct members of aH.

Suppose, ahi=ahj⇒hi=hj be the cancellation law of G.

Because G is a finite group, there will be a finite number of discrete left cosets, say p. As a result, m=np since the total number of elements in all cosets equals np, which is equal to the total number of elements in G.

p = m/n

This proves that n, H's order, is a divisor of m, the finite group G's order. We can also observe that the index p is a divisor of the group's order.

Hence, proved, |G| = |H|

Key takeaway

1. One of the most important theorems in abstract algebra is the Lagrange theorem.
2. It asserts that in group theory, the order of subgroup H of group G splits the order of G for any finite group G.
3. The number of elements is represented by the group's order. Joseph-Louis Lagrange proved this theorem.

2.7 Normal Subgroups

Let G stand for a group. If for any h ∈ H and x ∈ G, x h x-1∈ H, a subgroup H of G is said to be a normal subgroup of G.

If x H x-1 = {x h x-1| h ∈ H} then H is normal in G if and only if xH x-1⊆H, ∀ x∈ G.

Note- (G, *) is normal in (G, *). It is called the improper normal sub-graph of G.

Statement - Every subgroup H of G is normal in G if G is an abelian group.

Proof:

Allow any h ∈ H, x ∈ G, and then

x h x-1= x (h x-1)

x h x-1= (x x-1) h

x h x-1 = e h

x h x-1 = h∈ H

As a result, H is a normal subgroup of G.

2.8 Permutation and Symmetric groups

The set of all bijections from the set to itself with composition of functions as the group action is called a symmetric group on a set. The set of all permutations of the set's elements is known as the permutation group.

A "permutation group" is a group that acts (faithfully) on a set; this includes both symmetric groups (which are the groups of all permutations of the set) and subgroups of symmetric groups.

Although all groups can be realized as permutation groups (by acting on themselves), this type of action is rarely useful in studying the group; on the other hand, special types of actions (irreducible, faithful, transitive, doubly transitive, etc.) can provide a wealth of information about the group. Jordan, for example, established that A7, S6, S5, and the Mathieu group M12 are the only finite sharply five transitive groups.

(A "sharply five transitive group" is a group G acting on a set X with five or more components, such that there exists one and only one g ∈ G such that g. ai=bi for every ten elements a1,...,a5, b1,...,b5∈ X, with ai≠ aj for i ≠ j and bi ≠ bj for i ≠ j.)

(In fact, Jordan showed that the only finite sharply 𝑘-transitive groups for 𝑘≥4 are 𝑆k, 𝑆k+1, 𝐴k+2, 𝑀11, and 𝑀12.

A permutation group is composed of a group G and a faithful action: G×X →X on a set X (faithful here implies that if gx=x for all x, then g=e). Cayley's Theorem states that any group G can be thought of as a permutation group if X is the underlying set of G and multiplication is performed. However, because the set on which G acts is enormous, this results in an embedding of G into a very large symmetric group. If the set you're acting on is "small"-ish, you'll usually get additional information.

Cayley's Theorem was developed because, in the past, people only examined permutation groups: collections of functions that acted on sets (the sets of roots of a polynomial, the points on the plane via symmetries, etc.). Cayley was attempting to abstract the concept of group; however, he pointed out that his more abstract definition included all of the things that people were already thinking about, and that it did not introduce any new ones in the sense that any abstract group could be considered a permutation group.

Key takeaway

1. The set of all bijections from the set to itself with composition of functions as the group action is called a symmetric group on a set.
2. The set of all permutations of the set's elements is known as the permutation group.
3. Cayley's Theorem was developed because, in the past, people only examined permutation groups: collections of functions that acted on sets (the sets of roots of a polynomial, the points on the plane via symmetries, etc.).

2.9 Group Homomorphisms

A homomorphism is a mapping f: G →G' that has the properties f (xy) =f(x) f(y), ∀ x, y ∈ G. Despite the fact that the binary operations of the groups G and G' are different, the mapping f preserves the group operation. The homomorphism condition is the one described above.

Kernel of Homomorphism: -The set {x∈ G | f(x) =e'} is the Kernel of a homomorphism f from a group G to a group G' with identity e'.

Ker f stands for the kernel of f.

If f: G→G' is a homomorphism of G intoG', then f's image set is the range of the map f, indicated by f (G). Thus

Im (f) = f (G) = {f(x)∈ G'| x ∈G}

G' is considered a homomorphic image of G if f (G) =G'

Example: Let G be (Z, +) i.e., the group of integers under addition and let f: G →G defined by

∅(x) = 3x ∀x ∈G. Prove that f is homomorphism, determine its Kernel.

Solution: We have ∅(x) = 3x ∀x ∈G

∀x, y ∈G ⇒x + y ∈G (∴G is a group under addition)

Now

f(x + y) = 3 (x + y)

= 3x + 3y

= f (x) + f (y)

Hence f is homomorphism.

Kernel of homomorphism consists of half of zero i.e., the integers whose double is zero.

Thus K = {0}

Isomorphism

Let's consider two algebraic systems, (G1, *) and (G2,0), where * and 0 are both binary operations. If there is an isomorphic mapping f: G1→G2, the systems (G1, *) and (G2,0) are said to be isomorphic.

When two algebraic systems are structurally comparable, one can be produced from the other by merely keeping the elements and operations the same.

Example, consider the two algebraic systems (A1, *) and (A2,⊡) illustrated in fig. Determine the isomorphism of the two algebraic systems.

⊡	1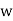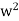
1	1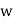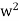
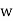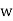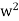			1
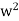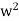		1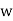

Solution - The two algebraic systems (A1, *) and (A2,⊡), respectively, are isomorphic, and (A2,⊡) is an isomorphic image of A1.

f(a)=1

f (b)=w

f (c)= w2

Automorphism

Let's consider two algebraic systems, (G1, *) and (G2,0), where * and 0 are binary operations on G1 and G2, respectively. If G1= G2, then an isomorphism from (G1, *) to (G2,0) is known as an automorphism.

Key takeaway

1. A homomorphism is a mapping f: G →G' that has the properties f (xy) =f(x) f(y), ∀ x, y ∈ G.
2. Despite the fact that the binary operations of the groups G and G' are different, the mapping f preserves the group operation.

2.10 Definition and elementary properties of Rings and Fields

A ring is an algebraic system (R, +,) that satisfies the following conditions: R is a set with two arbitrary binary operations + and.

1. (R, +) is an abelian group.
2. (R, ∙) is a semigroup.
3. The addition operation is distributive over the multiplication operation, i.e.,

a (b+c) =ab +ac and (b+c) a = ba + ca for all a, b, c ∈ R.

Example - Under the addition and multiplication modulo 9 operations, the set Z9 = 0, 1, 2, 3, 4, 5, 6, 7, 8 forms a ring.

Example: The set of integers Z, with respect to the operations + and × is a ring.

Types of Rings

1. Commutative Rings:

A commutative ring (R, +,) is defined as one that holds the commutative law under multiplication, i.e., a. b = b. a, for any a, b ∈ R.

Example, Consider a set E of all even numbers that is subjected to addition and multiplication operations. A commutative ring is formed by the set E.

2. Ring with Unity:

If a ring (R, +,) has a multiplicative identity, it is called a ring with unity.

Example, Consider a set M of all 2 x 2 matrices over integers that are subjected to matrix multiplication and addition. With unity 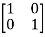, the set M forms a ring.

3. Ring with Zero Divisions:

If a.b=0, and a and b are any two non-zero R elements in the ring (R, +), then a and b are known as divisions of zero, and the ring (R, +) is known as ring with zero division.

4. Rings without Zero Division:

A ring without divisors of zero is an algebraic system (R, +) in which R is a set with two arbitrary binary operations + and we have a.b≠0 ⟹a≠0 and b ≠0 a for any a, b ∈ R.

Order of ring

The number of elements in a finite ring R is called the order of ring R. We denote this by |R|

Let (R, +, .) be a ring with unity. An element a 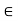R is said to be invertible, if there exists an element 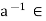R, called the inverse of a such that

a . 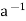= 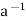. a = 1

Theorem- If R is a ring then:

(i) a . 0 = 0 = 0 . a ∀ a 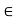R

(ii) a (–b) = (–a) b = –(ab) ∀ a, b 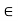R

(iii) (–a) (–b) = ab, for every a, b 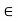R

Proof:

We know that

a + 0 = a ∀ a 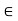R

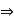a . (a + 0) = a ⋅ a

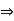a . a + a . 0 = a ⋅ a + 0

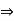a . 0 = 0 (by left cancellation under addition)

Similarly, we can prove

0 . a = 0

0 . a = 0

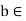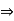(ii) R -b 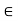R such that b + (–b) = 0

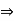a . (b + (-b)) = a ⋅ 0

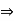a . b + a . (-b) = 0

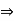a . (-b) = − (a . b)

Similarly, we can prove

(-a) . b = - (a . b)

(iii)

We have

a . (-b) + (-a) . (-b)

= (a + (-a)) . (-b)

= 0 . (-b)

= 0

= a . ((-b) + b)

= a . (-b) + a . b

By left cancellation law

(-a) . (-b) = a . b

Corollary: Let (R, +, .) be a ring, then

a . (b - c) = a . b - a . c

(b - c) . a = b . a - c . a for all a, b, c 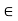R

Proof:

a . (b - c) = a . (b + (-c))

= a . b + a . (-c)

= a . b - a . c

Hence a . (b - c) = a . b - a . c

Similarly, we can prove that

(b - c) . a = b . a - c . a

Corollary: If (R, +, .) is a ring with unity then for all a 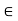R

(i) (-1) . a = - a

(ii) (-1) . (-1) = 1

Proof:

(i) (-1) . a = - (1 . a) = - a

(ii) R is a ring with unity element, then 1 . a = a ∀ a 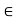R

We have (1)a + (-1) . a = 1 . a + (-1) . a

= (1 + (-1)) . a

= 0 . a

= 0

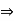a + (–1) a = 0

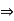(-1) . a = - a

If a = –1, then (-1) . (-1) = - (-1)

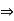(-1) . (-1) = 1

Definition (Field) - A commutative division ring is called a field.

Let Q be the set of rational numbers and ‘+’ and ‘.’ be two binary operation, then (Q, +, .) is a ring.

Q is field too.

Note-

1. A finite integral domain is a field.

2. The characteristic of the ring of integers (Z, +, .) is zero

3. The characteristic of an integral domain is either a prime or zero.

4. The characteristic of a field is either a prime or zero.

Key takeaway

1. A ring is an algebraic system (R, +,) that satisfies the following conditions: R is a set with two arbitrary binary operations + and.
2. A commutative division ring is called a field.

References:

1. Koshy, Discrete Structures, Elsevier Pub. 2008 Kenneth H. Rosen, Discrete Mathematics and Its Applications, 6/e, McGraw-Hill, 2006.

2. B. Kolman, R.C. Busby, and S.C. Ross, Discrete Mathematical Structures, 5/e, Prentice Hall, 2004.

3. E.R. Scheinerman, Mathematics: A Discrete Introduction, Brooks/Cole, 2000.

4. R.P. Grimaldi, Discrete and Combinatorial Mathematics, 5/e, Addison Wesley, 2004

5. Liptschutz, Seymour, “Discrete Mathematics”, McGraw Hill.