Unit – 4
Propositional and Predicate Logic
Mathematical logic principles define how to reason about mathematical statements. Aristotle, a Greek philosopher, is credited with inventing logical thinking. Many disciplines of mathematics and, as a result, computer science, have their theoretical foundations in logical reasoning. It has numerous applications in computer science, including the design of computing devices, artificial intelligence, and the construction of data structures for programming languages, among others.
Propositional logic is concerned with assertions that can be assigned the truth values "true" and "false." The goal is to evaluate these assertions individually and as a group.
Proposition
A proposition is a collection of declarative statements with either a truth value of "true" or "false." Propositional variables and connectives make up a propositional. The propositional variables are denoted by capital letters (A, B, etc). The connectives are used to link the propositional variables together.
Below are some instances of propositions.
● "Man is Mortal", it returns truth value “TRUE”
● "12 + 9 = 3 – 2", it returns truth value “FALSE”
The following does not constitute a proposition.
● "A is less than 2," says the narrator. It's because we can't tell if a statement is true or incorrect unless we give it a precise value of A.
Well formed formula
Examples of well-formed formulae:
● (¬a) (¬(¬a))
● (a ∧ (b ∧ c))
● (a → (b → c))
We omit parentheses whenever we may restore them through operator precedence:
Binds stronger
←
¬ ∧ ∨ → ↔
Truth tables
When the statement (P→Q)∨(Q→R) is true, we must decide. Using the connective definitions, we can see that for this to be true, either P→Q or Q→R must be true (or both). If P is false or Q is true (in the first case), and Q is false or R is true, then those are true (in the second case). So—yeah, things get a little tangled. Fortunately, we can create a chart to keep track of all the options.
Let's talk about truth tables. The notion is that for each of the sentential variables, we list a possible combination of Ts and Fs (for true and false), and then mark whether the statement in question is true or false in that case. This is done for every possible T and F combination.
This is done for every possible T and F combination. Then we can see whether the assertion is true or untrue in each situation. We will first fill in values for each element of the statement in order to divide up our effort into smaller, more manageable chunks for complicated statements.
Because the truth value of a statement is entirely decided by the truth values of its constituent parts and how they are related, all you need to know are the truth tables for each of the logical connectives. They are as follows:
P | Q | P∧Q |
| P | Q | P∨Q |
| P | Q | 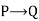 |
| P | Q | 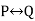 |
T T F F | T F T F | T F F F |
| T T F F | T F T F | T T T F |
| T T F F | T F T F | T F T T |
| T T F F | T F T F | T F F T |
The truth table for negation looks like this:
P | 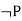 |
T F | F T |
Negation - It has the exact opposite meaning as the original sentence. If p is a statement, then ~p is the negation of p, which means 'it is not the case that p.' If p is true, then ~p is false, and vice versa.
Example - If p is the statement that Paris is in France, then ~ p is the statement that Paris is not in France.
p | ~ p |
T | F |
F | T |
Conjunction - It refers to the combining of two assertions. If p and q are two statements, then "p and q" is a compound statement represented by p q and referred to as "p and q's conjunction." Only when both p and q are true is the combination of p and q true. Otherwise, it's untrue.
p | q | p ∧ q |
T | T | T |
T | F | F |
F | T | F |
F | F | F |
Disjunction - It refers to the combining of two assertions. If p and q are two statements, then "p or q" is a compound statement indicated by p ∨ q and known as the p and q disjunction. When at least one of the two statements is true, the disjunction of p and q is true, and it is false only when both p and q are false.
p | q | p ∨ q |
T | T | T |
T | F | T |
F | T | T |
F | F | F |
Implication / if-then (⟶) - The proposition "if p, then q" is an implication p⟶q. If p is true and q is false, it is false. The remainder of the scenarios are correct.
p | q | p ⟶ q |
T | T | T |
T | F | F |
F | T | T |
F | F | F |
If and Only If (↔) - p ↔ q is a bi-conditional logical connective that holds true when p and q are the same, i.e., when both are false or true.
p | q | p ↔ q |
T | T | T |
T | F | F |
F | T | F |
F | F | T |
Tautology
In logic, a tautology is a proposition that is so phrased that it cannot be refuted without causing inconsistency. As a result, the statement "All humans are mammals" is taken to mean that anything is either a person or a mammal. However, that universal "truth" is derived solely from the actual use of the terms "human" and "mammal," and is thus entirely a question of definition.
The concept of tautology in the propositional calculus was first created by American philosopher Charles Sanders Peirce, the founder of the school of pragmatism and a notable logician, in the early twentieth century. However, the term was coined by the Austrian-born British philosopher Ludwig Wittgenstein, who claimed in his Logisch-philosophische Abhandlung (1921; Tractatus Logico-Philosophicus, 1922) that all necessary propositions are tautologies and that, as a result, all necessary propositions say the same thing—namely, nothing at all.
A tautology is a formula that holds true regardless of the value of its propositional variables.
Example − Prove [(A→B)∧A]→B is a tautology
The following is the truth table:
A | B | A → B | (A →B) ∧ A | [(A→B) ∧ A] → B |
True | True | True | True | True |
True | False | False | False | True |
False | True | True | False | True |
False | False | True | False | True |
As the final column contains all T's, so it is a tautology.
Satisfiability
A satisfying sentence is one in which the variables have a truth value assignment that makes the sentence true (truth value = t).
• Algorithm? • Try out all of the different assignments to discover which one works best.
The phrase is true because all of the truth values assigned to the variables are true.
• What is an algorithm? • Try out all of the possible assignments and make sure they all work.
Are there any algorithms that are superior than these?
Satisfiability problem
Many problems can be expressed as a list of constraints. Answer is assignment to variables that satisfy all the constraints.
Examples:
Scheduling people to work in shifts at a hospital
– Some people don’t work at night
– No one can work more than x hours a week
– Some pairs of people can’t be on the same shift
– Is there assignment of people to shifts that satisfy all constraints?
Finding bugs in programs
– Write logical specification of, e.g. Air traffic controller
– Write assertion “two airplanes on same runway at same time”
– Can these be satisfied simultaneously?
Contradiction
A formula that is always untrue for every value of its propositional variables is called a contradiction.
Example − Prove (A∨B)∧[(¬A)∧(¬B)] is a contradiction
The following is the truth table:
A | B | A ∨ B | ¬ A | ¬ B | (¬A) ∧ (¬B) | (A∧B) ∧ [(¬A) ∧ (¬B)] |
True | True | True | False | False | False | False |
True | False | True | False | True | False | False |
False | True | True | True | False | False | False |
False | False | False | True | True | True | False |
Algebra of proposition
A "sum-of-products" or disjunctive form is equivalent to every propositional formula. A disjunctive form is essentially an OR of AND-terms, where each AND-term is an AND of variables or variables' negations.
Conjunctive forms
If a compound statement is generated by operating AND among variables (negation of variables included) connected with ORs, it is said to be in conjunctive normal form. It is a compound statement formed by Intersection among variables connected with Unions in terms of set operations.
Example
● (A∨B)∧(A∨C)∧(B∨C∨D)
● (P∪Q)∩(Q∪R)
Disjunctive forms
If a compound statement is generated by operating OR among variables coupled with ANDs (negation of variables included), it is in disjunctive normal form. It's a compound statement derived from the union of variables linked to Intersections.
Example
● (A∧B)∨(A∧C)∨(B∧C∧D)
● (P∩Q)∪(Q∩R)
Theory of Inference
Modus ponens is the basic inference rule. It says that if both P → Q and P hold, Q can be deduced, and it's written as
P
P → Q
----------
Q
The premises are the lines above the dotted line, and the conclusion formed from the premises is the line below it.
If both "if it rains, the game is not played" and "it rains," for example, we can deduce that the game is not played.
In addition to modus ponens, identities and implications can be used to argue.
When the left(right) hand side of a statement's identity is substituted by the right(left) hand side of the identity, the resulting proposition is logically equal to the original proposition. As a result, the new proposition is derived from the old. For example in the proposition P ⋀ (Q → R), (Q → R) can be replaced with (ㄱQ ⋁ R) to conclude P (Q → R), since (Q → R) ⇔ (ㄱQ ⋁ R).
If the right(left) hand side of an implication of a proposition is substituted by the left(right) hand side of the implication, the resulting proposition is logically implied by the original proposition. As a result, the new proposition is derived from the old.
As illustrated below, the tautologies described as "implications" can also be considered inference rules.
Rules of Inference | Tautological form | Name |
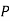 ---- 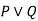 | 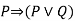 | Addition |
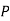 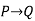 ------- 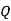 | 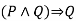 | Simplification |
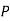 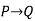 -------- 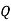 | 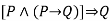 | Modus ponens |
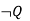 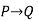 ------- 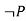 | 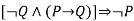 | Modus tollens |
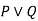 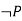 | 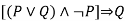 | Disjunctive syllogism |
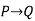 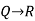 --------- 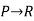 | 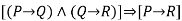 | Hypothetical syllogism |
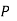 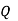 ------- 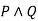 |
| Conjunction |
Example
Consider the following proposition:
1. Is it Tuesday or Wednesday today?
2. But it can't be Wednesday because the doctor's office is open today, and Wednesdays are typically closed.
3. As a result, today is Tuesday.
As seen below, this chain of reasoning (inferencing) can be expressed as a succession of modus ponens applications to the appropriate propositions.
The modus ponens is an inference rule that deduces Q from P -> Q and P -> Q and P -> Q and P -> Q and P -> Q and P -> Q and P -> Q and P -> Q
T: It's the second day of the week.
W: It's Wednesday today.
D: Today the doctor's office is open.
C: On Wednesdays, the doctor's office is always closed.
Key takeaway
- Propositional logic is concerned with assertions that can be assigned the truth values "true" and "false."
- The goal is to evaluate these assertions individually and as a group.
- Propositional variables and connectives make up a propositional. The propositional variables are denoted by capital letters (A, B, etc).
- A tautology is a formula that holds true regardless of the value of its propositional variables.
- A formula that is always untrue for every value of its propositional variables is called a contradiction.
- A "sum-of-products" or disjunctive form is equivalent to every propositional formula. A disjunctive form is essentially an OR of AND-terms, where each AND-term is an AND of variables or variables' negations.
Predicate Logic deals with predicates, which are propositions containing variables.
First order predicate
A predicate is a set of one or more variables that are defined on a certain domain. A variable-based predicate can be turned into a proposition by either assigning a value to the variable or quantifying it.
Some examples of predicates are as follows:
● Let E(x, y) denote "x = y"
● Let X(a, b, c) denote "a + b + c = 0"
● Let M(x, y) denote "x is married to y"
Well formed formula of predicate
The Well Formed Formula (wff) is a predicate that holds one or more of the following:
● Wffs are used for all propositional constants and variables.
● If x is a variable and Y is a wff, ∀xY and ∃xY are also wff
● Truth value and false values are wffs
● Each atomic formula is a wff
● All connectives connecting wffs are wffs
Quantifiers
Quantifiers quantify the variable of predicates. In predicate logic, there are two types of quantifiers: Universal Quantifier and Existential Quantifier.
Universal Quantifier
The assertions within its scope are true for every value of the particular variable, according to the universal quantifier. It's represented by the symbol ∀.
∀xP(x) is read as for every value of x, P(x) is true.
Example - "Man is mortal" can be translated into the propositional form xP(x), where P(x) implies that x is mortal and that the universe of discourse is made up of all men.
Existential Quantifier
The assertions within its scope are true for some values of the specified variable, according to the existential quantifier. It's represented by the symbol ∃.
∃xP(x) is read as for some values of x, P(x) is true.
Example - "Some people are dishonest," for example, can be translated into the propositional form xP(x), with P(x) denoting x is dishonest and some people denoting the universe of discourse.
Nested Quantifiers
The term "nested quantifier" refers to a quantifier that appears within the scope of another quantifier.
Example - ∀ a∃bP(x,y) where P(a,b) denotes a+b=0
∀ a∀b∀cP(a,b,c) where P(a,b) denotes a+(b+c)=(a+b)+c
Inference theory of predicate logic
A series of claims is referred to as an argument. The conclusion is the last assertion, and the premises are the ones before it (or hypothesis). Before the conclusion, the symbol "∴" (read thus) is placed. The conclusion of a valid argument flows from the truth values of the premises.
The templates or instructions for creating valid arguments from the statements we already know are provided by Rules of Inference.
Simple arguments can be used as the foundation for more complex valid arguments. Certain simple arguments that have been proven to be true are extremely essential in terms of their application. These are known as Rules of Inference arguments.
The most widely used Inference Rules are listed below —
Rules of Inference | Tautological form | Name |
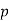 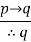 | 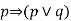 | Modus Ponens |
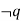 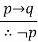
| 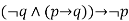 | Modus Tollens |
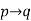 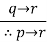 | 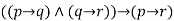 | Hypothetical syllogism |
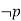 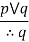 | 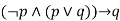
| Disjunctive syllogism |
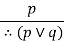 | 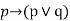 | Addition |
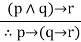 | 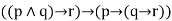 | Exportation |
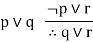 | 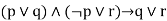 | Resolution |
Similarly, we have Rules of Inference for quantified statements –
Rule of Inference | Name |
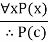 | Universal instantiation |
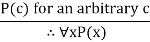 | Universal generalization |
 | Existential instantiation |
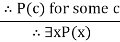 | Existential generalization |
Key takeaway
- Predicate Logic deals with predicates, which are propositions containing variables.
- A predicate is a set of one or more variables that are defined on a certain domain.
- A variable-based predicate can be turned into a proposition by either assigning a value to the variable or quantifying it.
- Quantifiers quantify the variable of predicates. In predicate logic, there are two types of quantifiers: Universal Quantifier and Existential Quantifier.
- A series of claims is referred to as an argument. The conclusion is the last assertion, and the premises are the ones before it (or hypothesis).
References:
1. Koshy, Discrete Structures, Elsevier Pub. 2008 Kenneth H. Rosen, Discrete Mathematics and Its Applications, 6/e, McGraw-Hill, 2006.
2. B. Kolman, R.C. Busby, and S.C. Ross, Discrete Mathematical Structures, 5/e, Prentice Hall, 2004.
3. E.R. Scheinerman, Mathematics: A Discrete Introduction, Brooks/Cole, 2000.
4. R.P. Grimaldi, Discrete and Combinatorial Mathematics, 5/e, Addison Wesley, 2004
5. Liptschutz, Seymour, “Discrete Mathematics”, McGraw Hill.