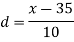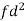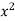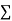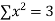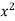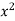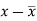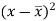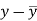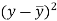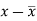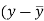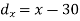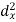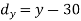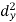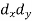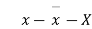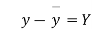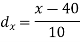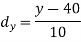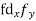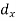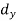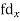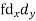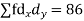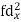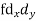Unit-3
Statistical techniques-1
Professor Bowley defines the average as-
“Statistical constants which enable us to comprehend in a single effort the significance of the whole”
An average is a single value that is the best representative for a given data set.
Measures of central tendency show the tendency of some central values around which data tend to cluster.
The following are the various measures of central tendency-
1. Arithmetic mean
2. Median
3. Mode
4. Weighted mean
5. Geometric mean
6. Harmonic mean
The arithmetic mean or mean-
The arithmetic mean is a value which is the sum of all observation divided by a total number of observations of the given data set.
If there are n numbers in a dataset- 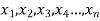 then the arithmetic mean will be-
then the arithmetic mean will be-
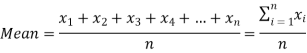
If the numbers along with frequencies are given then mean can be defined as-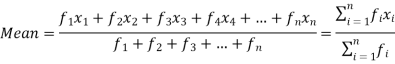
Example-1: Find the mean of 26, 15, 29, 36, 35, 30, 14, 21, 25 .
Sol.
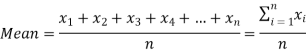
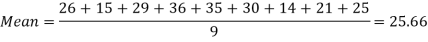
Example-2: Find the mean of the following dataset.
x | 20 | 30 | 40 |
f | 5 | 6 | 4 |
Sol.
We have the following table-
x | f | Fx |
20 | 5 | 100 |
30 | 6 | 180 |
40 | 7 | 160 |
| Sum = 15 | Sum = 440 |
Then Mean will be-
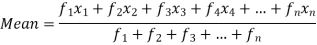
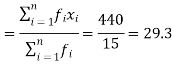
The direct method to find mean-
Example: Find the arithmetic mean of the following dataset-

Sol.
We have the following distribution-
Class interval | Mid value (x) | Frequency (f) | Fx |
0-10 | 05 | 3 | 15 |
10-20 | 15 | 5 | 75 |
20-30 | 25 | 7 | 175 |
30-40 | 35 | 9 | 315 |
40-50 | 45 | 4 | 180 |
|
| Sum = 28 | Sum = 760 |
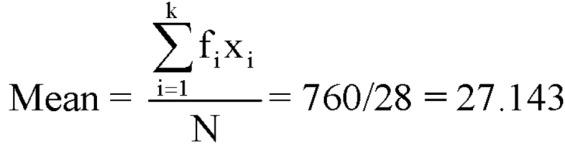
Short cut method to find mean-
Suppose ‘a’ is assumed mean, and ‘d’ is the deviation of the variate x form a, then-
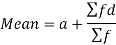
Example: Find the arithmetic mean of the following dataset.
Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
Frequency | 7 | 8 | 20 | 10 | 5 |
Sol.
Let the assumed mean (a) = 25,
Class | Mid-value | Frequency | x – 25 = d | fd |
0-10 | 5 | 7 | -20 | -140 |
10-20 | 15 | 8 | -10 | -80 |
20-30 | 25 | 20 | 0 | 0 |
30-40 | 35 | 10 | 10 | 100 |
40-50 | 45 | 5 | 20 | 100 |
Total |
| 50 |
| -20 |
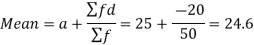
Step deviation method for mean-
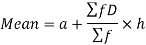
Where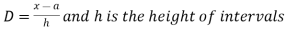
Median-
Median is the mid-value of the given data when it is arranged in ascending or descending order.
1. If the total number of values in the data set is odd then the median is the value of 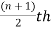 item.
item.
Note-The data should be arranged in ascending r descending order
2. If the total number of values in the data set is even then the median is the mean of the 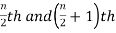 item.
item.
Example: Find the median of the data given below-
7, 8, 9, 3, 4, 10
Sol.
Arrange the data in ascending order-
3, 4, 7, 8, 9, 10
So there total 6 (even) observations, then-
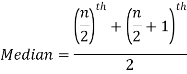
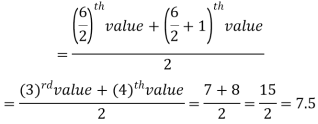
Median for grouped data-
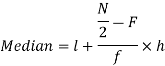
Here,
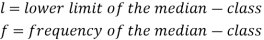
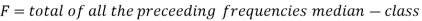
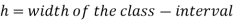
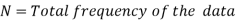
Example: Find the median of the following dataset-

Sol.
Class interval | Frequency | Cumulative frequency |
0 - 10 | 3 | 3 |
10 – 20 | 5 | 8 |
20 – 30 | 7 | 15 |
30 – 40 | 9 | 24 |
40 – 50 | 4 | 28 |
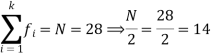
So that median class is 20-30.
Now putting the values in the formula-
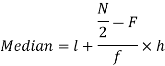
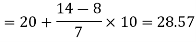
So that the median is 28.57
Mode-
A value in the data which is most frequent is known as a mode.
Example: Find the mode of the following data points-
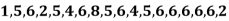
Sol. Here 6 has the highest frequency so that the mode is 6.
Mode for grouped data-
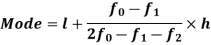
Here,
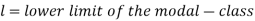
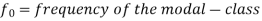
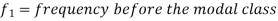
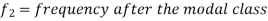
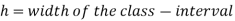
Example: Find the mode of the following dataset-

Sol.
Class interval | Frequency |
0 - 10 | 3 |
10 – 20 | 5 |
20 – 30 | 7 |
30 – 40 | 9 |
40 – 50 | 4 |
Here the highest frequency is 9. So that the modal class is 40-50,
Put the values in the given data-
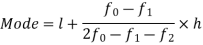
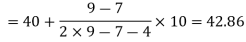
Hence the mode is 42.86
Note-
Mean – Mode = [Mean - Median]
Geometric Mean-
If 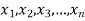 are the values of the data, then the geometric mean-
are the values of the data, then the geometric mean-
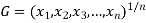
Harmonic mean-
The harmonic mean is the reciprocal of the arithmetic mean-
It can be defined as-
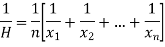
Note-
1. 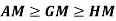
2. 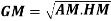
The rth moment of a variable x about the mean x is usually denoted by is given by
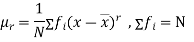
The rth moment of a variable x about any point a is defined by
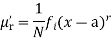
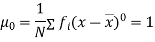
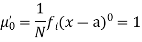
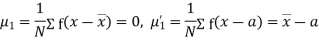
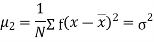
The relation between moments about mean and moment about any point:
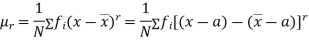
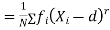 where
where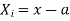 and
and 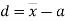
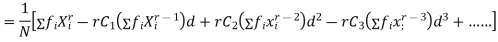
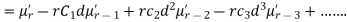
In particular
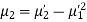
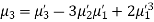
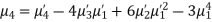
Note. 1. The sum of the coefficients of the various terms on the right-hand side is zero.
2. The dimension of each term on the right‐hand side is the same as that of terms on the left.
MOMENT GENERATING FUNCTION
The moment generating function of the variate 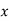 about
about 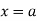 is defined as the expected value of
is defined as the expected value of 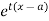 and is denoted
and is denoted 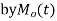 .
.
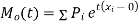
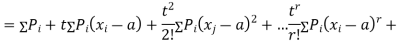
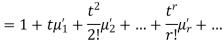
where 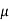 , ‘ is the moment of order
, ‘ is the moment of order 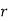 about
about 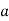
Hence 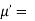 coefficient of
coefficient of  or
or 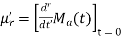
again 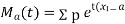 )
) 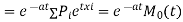
Thus the moment generating function about the point 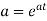 moment generating function about the origin.
moment generating function about the origin.
Skewness-
The word skewness means lack of symmetry-
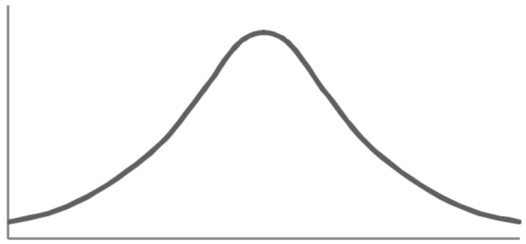
The examples of the symmetric curve, positively skewed, and negatively skewed curves are given as follows-
1. Symmetric curve-
2. Positively skewed-
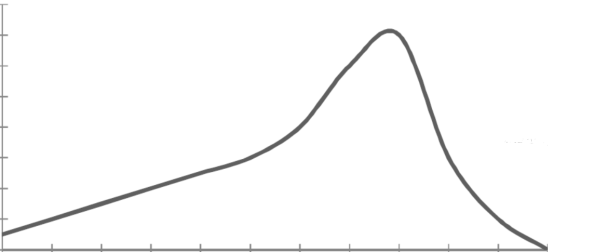
3. Negatively skewed-
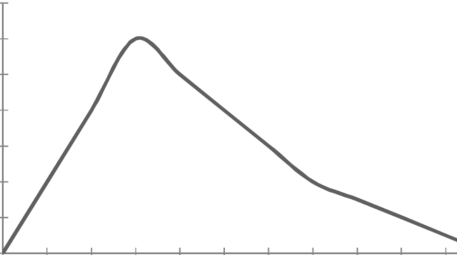
To measure the skewness we use Karl Pearson’s coefficient of skewness.
Then the formula is as follows-
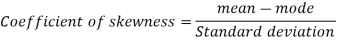
Note- the value of Karl Pearson’s coefficient of skewness lies between -1 to +1.
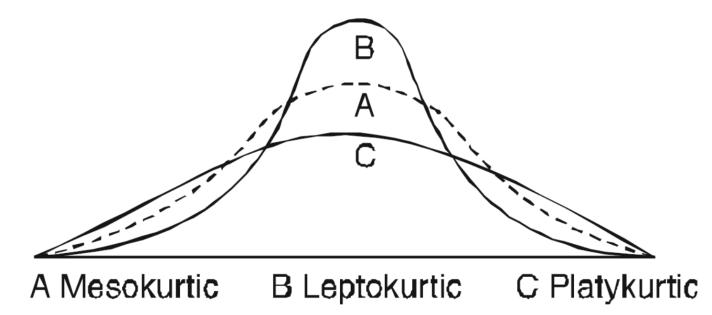
Kurtosis-
It is the measurement of the degree of peakedness of a distribution
Kurtosis is measured as-
Calculation of kurtosis-
The second and fourth central moments are used to measure kurtosis.
We use Karl Pearson’s formula to calculate kurtosis-
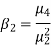
Now, three conditions arise-
1. If 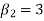 , then the curve is mesokurtic.
, then the curve is mesokurtic.
2. If 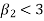 , then the curve is platykurtic
, then the curve is platykurtic
3. if 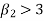 , then the curve is said to be leptokurtic.
, then the curve is said to be leptokurtic.
Example: If the coefficient of skewness is 0.64. The standard deviation is 13 and mean is 59.2, then find the mode and median.
Sol.
We know that-
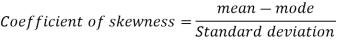
So that-
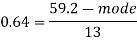
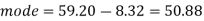
And we also know that-
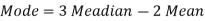
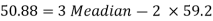
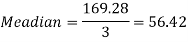
Example: Calculate Karl Pearson’s coefficient of skewness of marks obtained by 150 students.

Sol. The mode is not well defined so that first we calculate mean and median-
Class | f | x | CF |
| fd |
|
0-10 | 10 | 5 | 10 | -3 | -30 | 90 |
10-20 | 40 | 15 | 50 | -2 | -80 | 160 |
20-30 | 20 | 25 | 70 | -1 | -20 | 20 |
30-40 | 0 | 35 | 70 | 0 | 0 | 0 |
40-50 | 10 | 45 | 80 | 1 | 10 | 10 |
50-60 | 40 | 55 | 120 | 2 | 80 | 160 |
60-70 | 16 | 65 | 136 | 3 | 48 | 144 |
70-80 | 14 | 75 | 150 | 4 | 56 | 244 |
Now,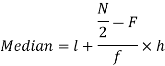
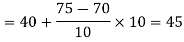
And
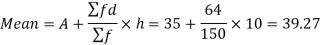
Standard deviation-
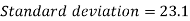
Then-
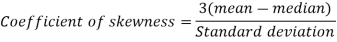
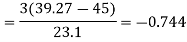
Example. The first four moments about the working mean 28.5 of distribution are 0.2 94, 7.1 44, 42.409, and 454.98. Calculate the moments about the mean. Also, evaluate 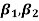 and comment upon the skewness and kurtosis of the distribution.
and comment upon the skewness and kurtosis of the distribution.
Solution. The first four moments about the arbitrary origin 28.5 are 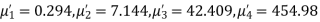
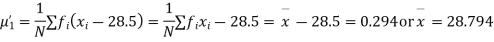
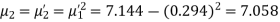
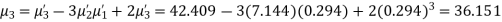
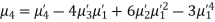
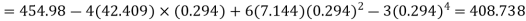
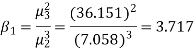
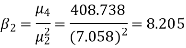
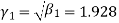 , which indicates considerable skewness of the distribution.
, which indicates considerable skewness of the distribution.
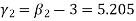 , which shows that the distribution is leptokurtic.
, which shows that the distribution is leptokurtic.
Example. Calculate the median, quartiles, and the quartile coefficient of skewness from the following data:
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140=150 |
No. of persons | 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
Solution. Here total frequency 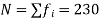
The cumulative frequency table is
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140=150 |
Frequency | 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
Cumulative Frequency | 12 | 30 | 65 | 107 | 157 | 202 | 222 | 230 |
Now, N/2 =230/2= 115th item which lies in the 110 – 120 group.
Median or 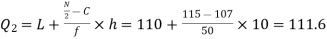
Also, 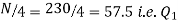 is 57.5th or 58th item which lies in the 90-100 group.
is 57.5th or 58th item which lies in the 90-100 group.
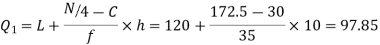
Similarly 3N/4 = 172.5 i.e. 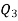 is 173rd item which lies in the 120-130 group.
is 173rd item which lies in the 120-130 group.
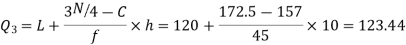
Hence quartile coefficient of skewness = 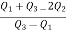
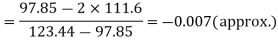
Method of Least Squares
Let 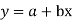 (1)
(1)
Be the straight line to be fitted to the given data points
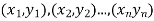
Let 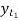 be the theoretical value for
be the theoretical value for 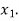
Then, 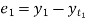
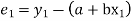
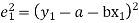
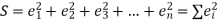

For S to be minimum
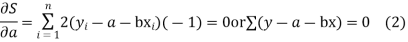
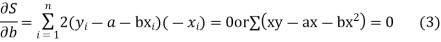
On simplification equation (2) and (3) becomes
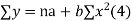
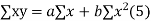
The equation (3) and (4) are known as Normal equations.
On solving ( 3) and (4) we get the values of a and b
(b)To fit the parabola
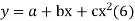
The normal equations are 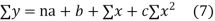
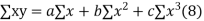
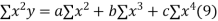
On solving three normal equations we get the values of a,b and c.
Example. Find the best values of a and b so that y = a + bx fits the data given in the table
x | 0 | 1 | 2 | 3 | 4 |
y | 1.0 | 2.9 | 4.8 | 6.7 | 8.6 |
Solution.
y = a + bx
x | y | xy |
|
0 | 1.0 | 0 | 0 |
1 | 2.9 | 2.0 | 1 |
2 | 4.8 | 9.6 | 4 |
3 | 6.7 | 20.1 | 9 |
4 | 8.6 | 13.4 | 16 |
|
|
|
|
Normal equations, 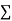 y= na+ b
y= na+ b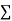 x (2)
x (2)
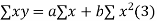
On putting the values of 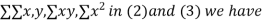
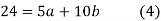
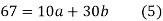
On solving (4) and (5) we get,
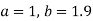
On substituting the values of a and b in (1) we get
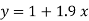
Example. Find the least-squares approximation of second degree for the discrete data
X | 2 | -1 | 0 | 1 | 2 |
Y | 15 | 1 | 1 | 3 | 19 |
Solution. Let the equation of second-degree polynomial be 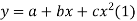
X | y | xy |
|
|
|
|
-2 | 15 | -30 | 4 | 60 | -8 | 16 |
-1 | 1 | -1 | 1 | 1 | -1 | 1 |
0 | 1 | 0 | 0 | 0 | 0 | 0 |
1 | 3 | 3 | 1 | 3 | 1 | 1 |
2 | 19 | 38 | 4 | 76 | 8 | 16 |
|
|
|
|
|
|
|
Normal equations are 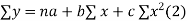
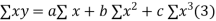
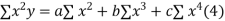
On putting the values of 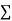 x,
x, 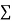 y,
y,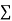 xy,
xy, 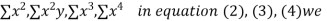 have
have
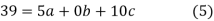
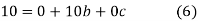
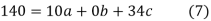
On solving (5),(6),(7), we get, 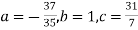
The required polynomial of the second degree is
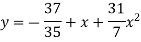
Example: Find the straight line that best fits the following data by using the method of least square.
X | 1 | 2 | 3 | 4 | 5 |
y | 14 | 27 | 40 | 55 | 68 |
Sol.
Suppose the straight line
y = a + bx…….. (1)
Fits the best-
Then-
x | y | xy |
|
1 | 14 | 14 | 1 |
2 | 27 | 54 | 4 |
3 | 40 | 120 | 9 |
4 | 55 | 220 | 16 |
5 | 68 | 340 | 25 |
Sum = 15 | 204 | 748 | 55 |
Normal equations are-
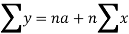
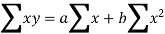
Put the values from the table, we get two normal equations-
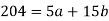
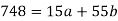
On solving the above equations, we get-
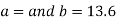
So that the best fit line will be- (on putting the values of a and b in equation (1))
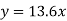
Second-degree parabolas and more general curves
To fit the second-degree parabola-
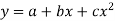
The normal equations will be-
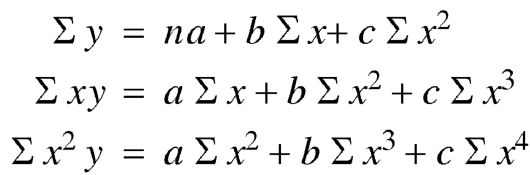
Note- Change of scale-
We change the scale if the data is large and given at equal intervals.
As-
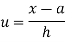
Example: Fit the second-degree parabola of the following data by using the method of least squares.
X | 1929 | 1930 | 1931 | 1932 | 1933 | 1934 | 1935 | 1936 | 1937 |
Y | 352 | 356 | 357 | 358 | 360 | 361 | 361 | 360 | 359 |
Sol.
By taking u = x – 1933 and v = y – 357
Then equation 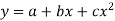 becomes
becomes 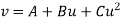
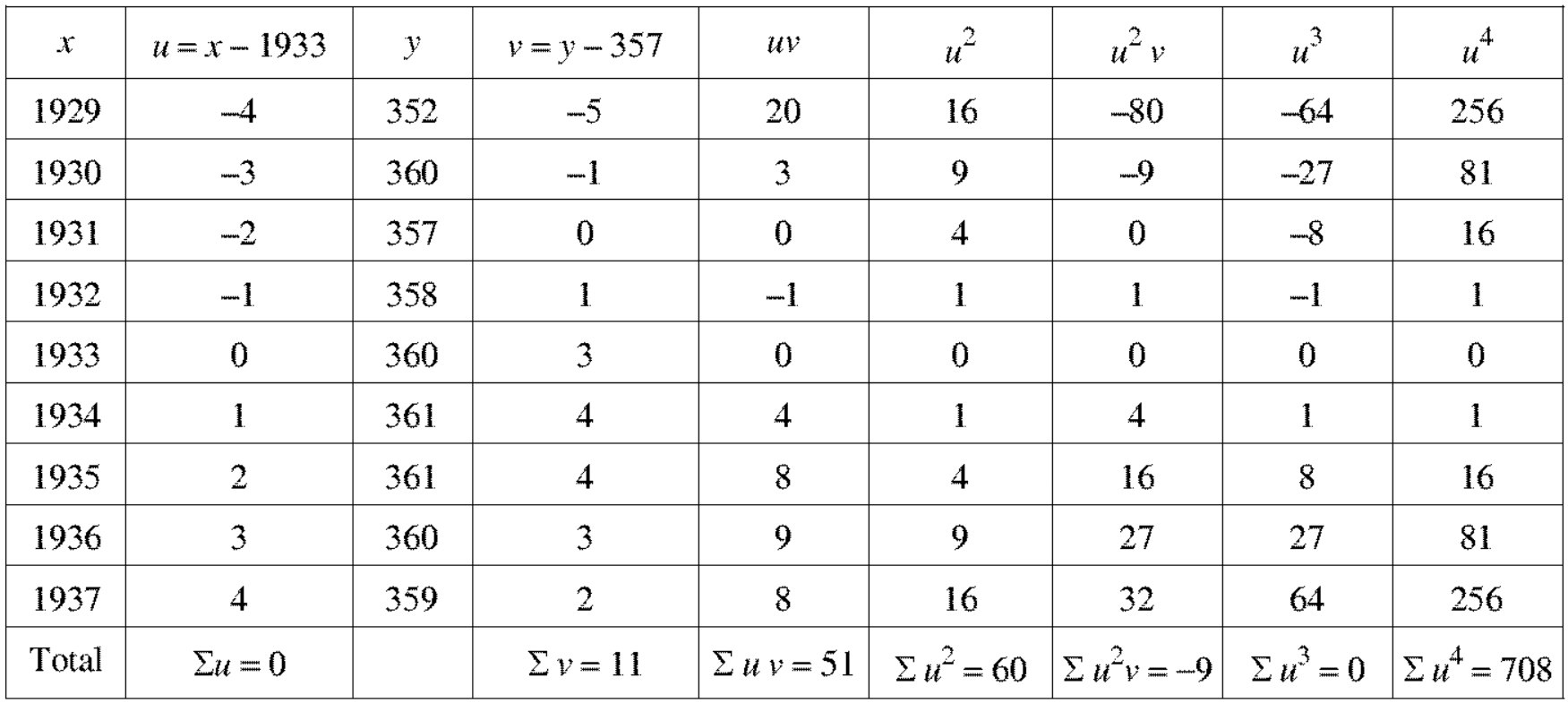
Putting the values from the table in normal equations-
We get-
11 = 3A + 0B + 60C or 11 = 9A + 60C
51 = 0A + 60B + 0C or B = 17 / 20
-9 = 60A + 0B + 708C or -9 = 60A + 708C
On solving, we get-
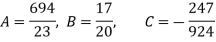
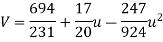
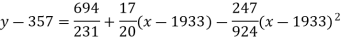
On solving the above equation, we get-
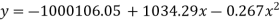
Example: Fit the curve 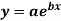 by using the method of least square.
by using the method of least square.
X | 1 | 2 | 3 | 4 | 5 | 6 |
Y | 7.209 | 5.265 | 3.846 | 2.809 | 2.052 | 1.499 |
Sol.
Here-
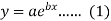
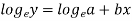
Now put-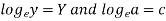
Then we get-
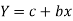
x | Y |
| xY |
|
1 | 7.209 | 1.97533 | 1.97533 | 1 |
2 | 5.265 | 1.66108 | 3.32216 | 4 |
3 | 3.846 | 1.34703 | 4.04109 | 9 |
4 | 2.809 | 1.03283 | 4.13132 | 16 |
5 | 2.052 | 0.71881 | 3.59405 | 25 |
6 | 1.499 | 0.40480 | 2.4288 | 36 |
Sum = 21 |
| 7.13988 | 19.49275 | 91 |
Normal equations are-
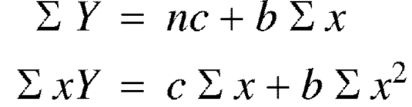
Putting the values form the table, we get-
7.13988 = 6c + 21b
19.49275 = 21c + 91b
On solving, we get-
b = -0.3141 and c = 2.28933
c = 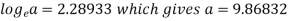
Now put these values in equations (1), we get-
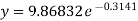
When two variables are related in such a way that a change in the value of one variable affects the value of the other variable, then these two variables are said to be correlated and there is a correlation between two variables.
Example- Height and weight of the persons of a group.
The correlation is said to be a perfect correlation if two variables vary in such a way that their ratio is constant always.
Scatter diagram-
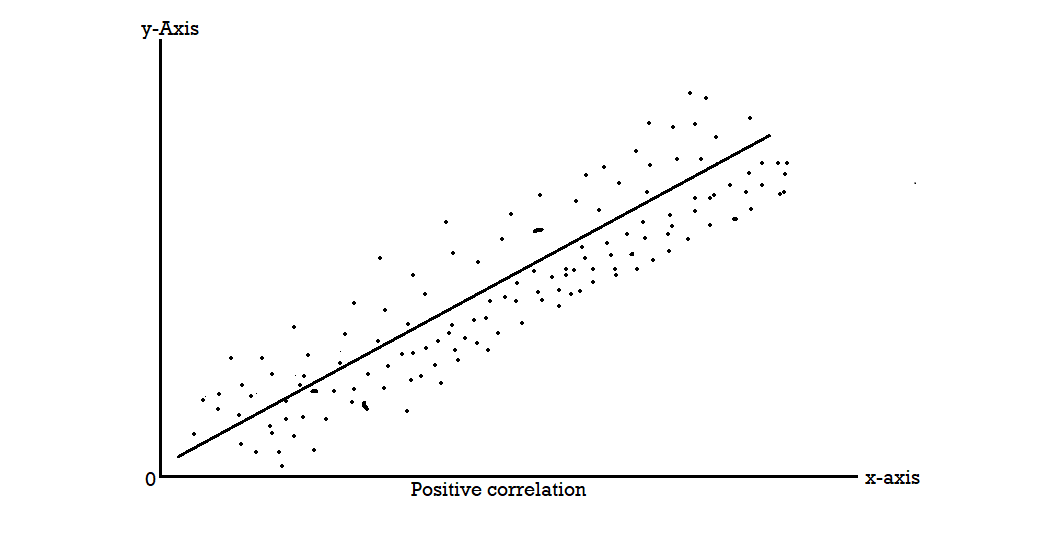
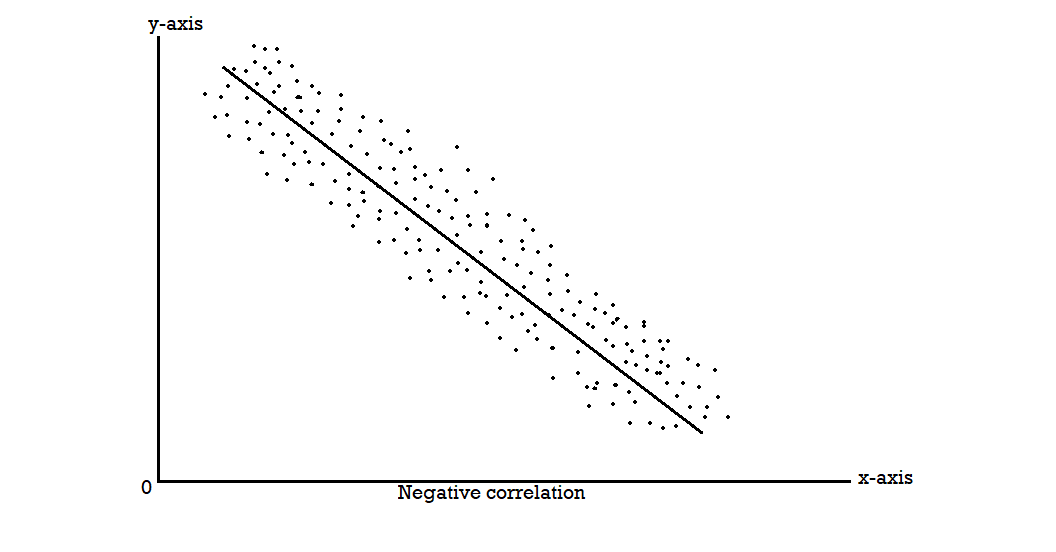
Karl Pearson’s coefficient of correlation-
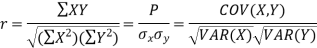
Here- 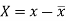 and
and 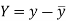
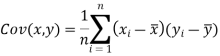
Note-
1. Correlation coefficient always lies between -1 and +1.
2. Correlation coefficient is independent of the change of origin and scale.
3. If the two variables are independent then the correlation coefficient between them is zero.
Correlation coefficient | Type of correlation |
+1 | Perfect positive correlation |
-1 | Perfect negative correlation |
0.25 | Weak positive correlation |
0.75 | Strong positive correlation |
-0.25 | Weak negative correlation |
-0.75 | Strong negative correlation |
0 | No correlation |
Example: Find the correlation coefficient between age and weight of the following data-
Age | 30 | 44 | 45 | 43 | 34 | 44 |
Weight | 56 | 55 | 60 | 64 | 62 | 63 |
Sol.
X | y |
|
|
|
| ( |
30 | 56 | -10 | 100 | -4 | 16 | 40 |
44 | 55 | 4 | 16 | -5 | 25 | -20 |
45 | 60 | 5 | 25 | 0 | 0 | 0 |
43 | 64 | 3 | 9 | 4 | 16 | 12 |
34 | 62 | -6 | 36 | 2 | 4 | -12 |
44 | 63 | 4 | 16 | 3 | 9 | 12 |
Sum= 240 |
360 |
0 |
202 |
0 |
70
|
32 |
Karl Pearson’s coefficient of correlation-
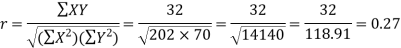
Here the correlation coefficient is 0.27.which is the positive correlation (weak positive correlation), this indicates that as age increases, the weight also increases.
Short-cut method to calculate correlation coefficient-
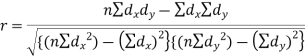
Here,
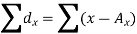
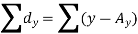
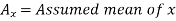
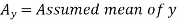
Example: Find the correlation coefficient between the values X and Y of the dataset given below by using the short-cut method-
X | 10 | 20 | 30 | 40 | 50 |
Y | 90 | 85 | 80 | 60 | 45 |
Sol.
X | Y |
|
|
|
|
|
10 | 90 | -20 | 400 | 20 | 400 | -400 |
20 | 85 | -10 | 100 | 15 | 225 | -150 |
30 | 80 | 0 | 0 | 10 | 100 | 0 |
40 | 60 | 10 | 100 | -10 | 100 | -100 |
50 | 45 | 20 | 400 | -25 | 625 | -500 |
Sum = 150 |
360 |
0 |
1000 |
10 |
1450 |
-1150 |
Short-cut method to calculate correlation coefficient-
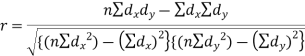
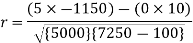
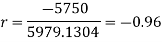
Example. Psychological tests of intelligence and Engineering ability were applied to 10 students. Here is a record of ungrouped data showing intelligence ratio (I.R) and Engineering ratio (E.R). Calculate the coefficient of correlation.
Student | A | B | C | D | E | F | G | H | I | J |
I.R. | 105 | 104 | 102 | 101 | 100 | 99 | 98 | 96 | 93 | 92 |
E.R. | 101 | 103 | 100 | 98 | 95 | 96 | 104 | 92 | 97 | 94 |
Solution. We construct the following table
Student | Intelligence ratio x | Engineering ratio y y |
|
| XY |
A | 105 6 | 101 3 | 36 | 9 | 18 |
B | 104 5 | 103 5 | 25 | 25 | 25 |
C | 102 3 | 100 2 | 9 | 4 | 6 |
D | 101 2 | 98 0 | 4 | 0 | 0 |
E | 100 1 | 95 -3 | 1 | 9 | -3 |
F | 99 0 | 96 - 2 | 0 | 4 | 0 |
G | 98 -1 | 104 6 | 1 | 36 | -6 |
H | 96 -3 | 92 -6 | 9 | 36 | 18 |
I | 93 -6 | 97 -1 | 36 | 1 | 6 |
J | 92 -7 | 94 -4 | 49 | 16 | 28 |
Total | 990 0 | 980 0 | 170 | 140 | 92 |
From this table, the mean of x, i.e. 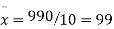 and mean of y, i.e.
and mean of y, i.e. 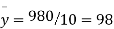
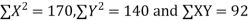
Substituting these value in the formula (1)p.744 we have
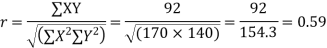
Example. The correlation table given below shows that the ages of husband and wife of 53 married couples living together on the census night of 1991. Calculate the coefficient of correlation between the age of the husband and that of the wife.
Age of husband | Age of wife | Total | ||||||
15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 | |||
15-25 | 1 | 1 | - | - | - | - | 2 | |
25-35 | 2 | 12 | 1 | - | - | - | 15 | |
35-45 | - | 4 | 10 | 1 | - | - | 15 | |
45-55 | - | - | 3 | 6 | 1 | - | 10 | |
55-65 | - | - | - | 2 | 4 | 2 | 8 | |
65-75 | - | - | - | - | 1 | 2 | 3 | |
Total | 3 | 17 | 14 | 9 | 6 | 4 | 53 | |
Solution.
Age of husband | Age of wife x series | Suppose
| |||||||||||
15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 |
Total f | |||||||
Years | Midpoint x | 20 | 30 | 40 | 50 | 60 | 70 | ||||||
Age group | Midpoint y |
|
| -20 | -10 | 0 | 10 | 20 | 30 |
|
|
| |
| -2 | -1 | 0 | 1 | 2 | 3 | |||||||
15-25 | 20 | -20 | -2 | 4 1 | 2 1 |
|
|
|
| 2 | -4 | 8 | 6 |
25-35 | 30 | -10 | -1 | 4 2 | 12 12 | 0 1 |
|
|
| 15 | -15 | 15 | 16 |
35-45 | 40 | 0 | 0 |
| 0 4 | 0 10 | 0 1 |
|
| 15 | 0 | 0 | 0 |
45-55 | 50 |
|
|
|
| 0 3 | 6 6 | 2 1 |
| 10 | 10 | 10 | 8 |
55-65 | 60 |
|
|
|
|
| 4 2 | 16 4 | 12 2 | 8 | 16 | 32 | 32 |
65-75 | 70 |
|
|
|
|
|
| 6 1 | 18 2 | 3 | 9 | 27 | 24 |
Total f | 3 | 17 | 14 | 9 | 6 | 4 | 53 = n | 16 | 92 | 86 | |||
| -6 | -17 | 0 | 9 | 12 | 12 | 10 | Thick figures in small sqs. for Check:
From both sides | |||||
| 12 | 17 | 0 | 9 | 24 | 36 | 98 | ||||||
| 8 | 14 | 0 | 10 | 24 | 30 | 86 | ||||||
With the help of the above correlation table, we have
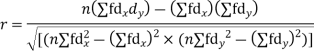
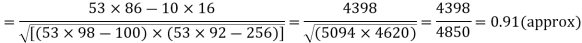
Spearman’s rank correlation-
When the ranks are given instead of the scores, then we use Spearman’s rank correlation to find out the correlation between the variables.
Spearman’s rank correlation coefficient can be defined as-
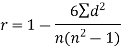
Example: Compute the Spearman’s rank correlation coefficient of the dataset given below-
Person | A | B | C | D | E | F | G | H | I | J |
Rank in test-1 | 9 | 10 | 6 | 5 | 7 | 2 | 4 | 8 | 1 | 3 |
Rank in test-2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Sol.
Person | Rank in test-1 | Rank in test-2 | d = |
|
A | 9 | 1 | 8 | 64 |
B | 10 | 2 | 8 | 64 |
C | 6 | 3 | 3 | 9 |
D | 5 | 4 | 1 | 1 |
E | 7 | 5 | 2 | 4 |
F | 2 | 6 | -4 | 16 |
G | 4 | 7 | -3 | 9 |
H | 8 | 8 | 0 | 0 |
I | 1 | 9 | -8 | 64 |
J | 3 | 10 | -7 | 49 |
Sum |
|
|
| 280 |
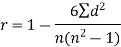
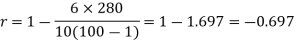
Example. Ten participants in a contest are ranked by two judges as follows:
x | 1 | 6 | 5 | 10 | 3 | 2 | 4 | 9 | 7 | 8 |
y | 6 | 4 | 9 | 8 | 1 | 2 | 3 | 10 | 5 | 7 |
Calculate the rank correlation coefficient 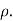
Solution. If 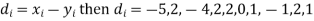
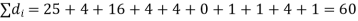
Hence, 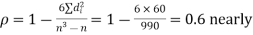
Example. Three judges A, B, C give the following ranks. Find which pair of judges has a common approach
A | 1 | 6 | 5 | 10 | 3 | 2 | 4 | 9 | 7 | 8 |
B | 3 | 5 | 8 | 4 | 7 | 10 | 2 | 1 | 6 | 9 |
C | 6 | 4 | 9 | 8 | 1 | 2 | 3 | 10 | 5 | 7 |
Solution. Here n = 10
A (=x) | Ranks by B(=y) | C (=z) |
x-y |
y - z |
z-x |
|
|
|
1 | 3 | 6 | -2 | -3 | 5 | 4 | 9 | 25 |
6 | 5 | 4 | 1 | 1 | -2 | 1 | 1 | 4 |
5 | 8 | 9 | -3 | -1 | 4 | 9 | 1 | 16 |
10 | 4 | 8 | 6 | -4 | -2 | 36 | 16 | 4 |
3 | 7 | 1 | -4 | 6 | -2 | 16 | 36 | 4 |
2 | 10 | 2 | -8 | 8 | 0 | 64 | 64 | 0 |
4 | 2 | 3 | 2 | -1 | -1 | 4 | 1 | 1 |
9 | 1 | 10 | 8 | -9 | 1 | 64 | 81 | 1 |
7 | 6 | 5 | 1 | 1 | -2 | 1 | 1 | 4 |
8 | 9 | 7 | -1 | 2 | -1 | 1 | 4 | 1 |
Total |
|
| 0 | 0 | 0 | 200 | 214 | 60 |
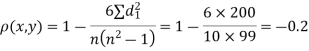
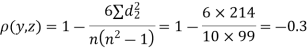
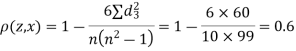
Since 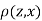 is maximum, the pair of judge A and C have the nearest common approach.
is maximum, the pair of judge A and C have the nearest common approach.
Regression-
Regression is the measure of the average relationship between the independent and dependent variable
Regression can be used for two or more than two variables.
There are two types of variables in regression analysis.
1. Independent variable
2. Dependent variable
The variable which is used for prediction is called the independent variable.
It is known as a predictor or regressor.
The variable whose value is predicted by an independent variable is called the dependent variable or regressed or explained variable.
The scatter diagram shows the relationship between the independent and dependent variable, then the scatter diagram will be more or less concentrated round a curve, which is called the curve of regression.
When we find the curve as a straight line then it is known as the line of regression and the regression is called linear regression.
Note- regression line is the best fit line that expresses the average relation between variables.
Equation of the line of regression-
Let
y = a + bx ………….. (1)
is the equation of the line of y on x.
Let 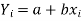 be the estimated value of
be the estimated value of 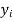 for the given value of
for the given value of 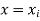 .
.
So that, According to the principle of least squares, we have the determined ‘a’ and ‘b’ so that the sum of squares of deviations of observed values of y from expected values of y,
That means-
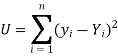
Or
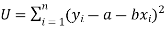 …….. (2)
…….. (2)
Is the minimum.
Form the concept of maxima and minima, we partially differentiate U with respect to ‘a’ and ‘b’ and equate to zero.
Which means
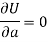
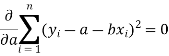
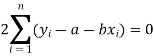
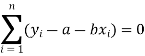
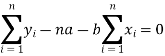
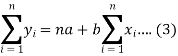
And
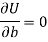
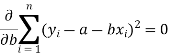
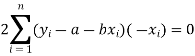
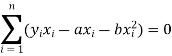
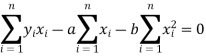
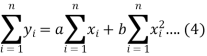
These equations (3) and (4) are known as the normal equation for a straight line.
Now divide equation (3) by n, we get-
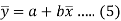
This indicates that the regression line of y on x passes through the point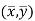 .
.
We know that-
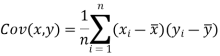
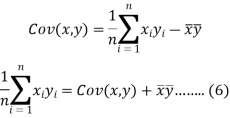
The variance of variable x can be expressed as-
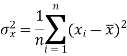
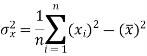
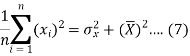
Dividing equation (4) by n, we get-
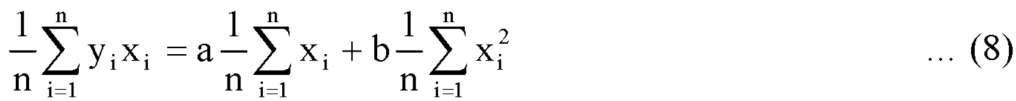
From equation (6), (7), and (8)-
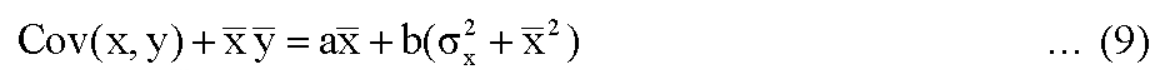
Multiply (5) by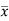 , we get-
, we get-
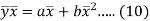
Subtracting equation (10) from equation (9), we get-
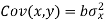

Since ‘b’ is the slope of the line of regression y on x and the line of regression passes through the point (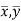 ), so that the equation of the line of regression of y on x is-
), so that the equation of the line of regression of y on x is-
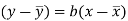
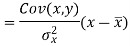
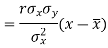
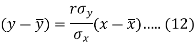
This is known as the regression line of y on x.
Note-
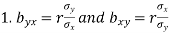 are the coefficients of regression.
are the coefficients of regression.
2. 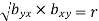
Example: Two variables X and Y are given in the dataset below, find the two lines of regression.
x | 65 | 66 | 67 | 67 | 68 | 69 | 70 | 71 |
y | 66 | 68 | 65 | 69 | 74 | 73 | 72 | 70 |
Sol.
The two lines of regression can be expressed as-
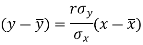
And
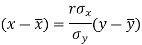
x | y |
|
| xy |
65 | 66 | 4225 | 4356 | 4290 |
66 | 68 | 4356 | 4624 | 4488 |
67 | 65 | 4489 | 4225 | 4355 |
67 | 69 | 4489 | 4761 | 4623 |
68 | 74 | 4624 | 5476 | 5032 |
69 | 73 | 4761 | 5329 | 5037 |
70 | 72 | 4900 | 5184 | 5040 |
71 | 70 | 5041 | 4900 | 4970 |
Sum = 543 | 557 | 36885 | 38855 | 37835 |
Now-
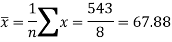
And
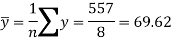
The standard deviation of x-
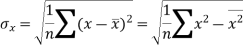

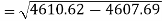
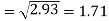
Similarly-
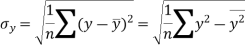
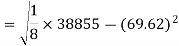
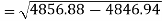
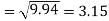
Correlation coefficient-
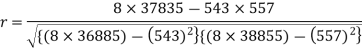
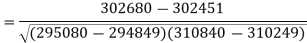
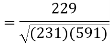
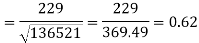
Put these values in the regression line equation, we get
Regression line y on x-
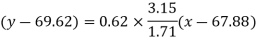
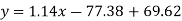
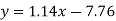
Regression line x on y-
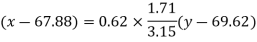
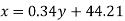
A regression line can also be found by the following method-
Example: Find the regression line of y on x for the given dataset.
X | 4.3 | 4.5 | 5.9 | 5.6 | 6.1 | 5.2 | 3.8 | 2.1 |
Y | 12.6 | 12.1 | 11.6 | 11.8 | 11.4 | 11.8 | 13.2 | 14.1 |
Sol.
Let y = a + bx is the line of regression of y on x, where ‘a’ and ‘b’ are given as-
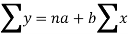
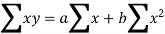
We will make the following table-
x | Y | Xy |
|
4.3 | 12.6 | 54.18 | 18.49 |
4.5 | 12.1 | 54.45 | 20.25 |
5.9 | 11.6 | 68.44 | 34.81 |
5.6 | 11.8 | 66.08 | 31.36 |
6.1 | 11.4 | 69.54 | 37.21 |
5.2 | 11.8 | 61.36 | 27.04 |
3.8 | 13.2 | 50.16 | 14.44 |
2.1 | 14.1 | 29.61 | 4.41 |
Sum = 37.5 | 98.6 | 453.82 | 188.01 |
Using the above equations we get-
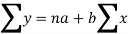
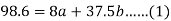
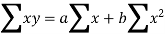
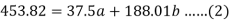
On solving these both equations, we get-
a = 15.49 and b = -0.675
So that the regression line is –
y = 15.49 – 0.675x
Note – Standard error of predictions can be found by the formula given below-
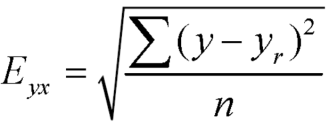
Difference between regression and correlation-
1. Correlation is the linear relationship between two variables while regression is the average relationship between two or more variables.
2. There are only limited applications of correlation as it gives the strength of the linear relationship while the regression is to predict the value of the dependent variable for the given values of independent variables.
3. Correlation does not consider dependent and independent variables while regression considers one dependent variable and other independent variables.
References
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. N.P. Bali and Manish Goyal, A textbook of Engineering Mathematics, Laxmi Publications.
3. P. G. Hoel, S. C. Port, and C. J. Stone, Introduction to Probability Theory, Universal Book Stall.
4. S. Ross, A First Course in Probability, 6th Ed., Pearson Education India,2002.