Unit 2
Regular Expressions and Languages
● Simple expressions called Regular Expressions can readily define the language adopted by finite automata. This is the most powerful way of expressing any language.
● Regular languages are referred to as the languages recognized by certain regular expressions.
● A regular expression may also be defined as a pattern sequence that defines a series.
● For matching character combinations in strings, regular expressions are used. This pattern is used by the string search algorithm to locate operations on a string.
A Regular Expression can be recursively defined as follows -
● ε is a Regular Expression indicates the language containing an empty string. (L (ε) = {ε})
● φ is a Regular Expression denoting an empty language. (L (φ) = { })
● x is a Regular Expression where L = {x}
● If X is a Regular Expression denoting the language L(X) and Y is a Regular Expression denoting the language L(Y), then
➢ X + Y is a Regular Expression corresponding to the language L(X) ∪ L(Y) where L(X+Y) = L(X) ∪ L(Y).
➢ X. Y is a Regular Expression corresponding to the language L(X). L(Y) where L(X.Y) = L(X) . L(Y)
➢ R* is a Regular Expression corresponding to the language L(R*) where L(R*) = (L(R))*
Example:
Write the regular expression beginning with a but not including consecutive b's for the language.
Sol: The regular expression has to be created for the language:
L = {a, aba, aab, aba, aaa, abab, ......}
It is possible to view the transition graph as a flowchart for a language recognizing algorithm. Three items consist of a transition graph:
- A finite set of states, some of which are designated as final states, and at least one of which is designated as the starting state.
- An alphabet of possible input symbols that form the input strings.
- A finite set of transitions that represent on a given input the change of state from the given state.
An effective path through the graph of transition is a set of edges that form a path starting at the beginning state and ending at one of the final states.
Some of the transition graphs are given below -
Fig. 1: Transition graph
The transition graph in above diagram shows DFA with minimum of one a and minimum of one b.
Kleen’s theorem states that an FA accepts any regular language and, conversely, that any language that an FA accepts is regular.
Theorem 1: A finite automatic acknowledges every normal language.
Proof: The general induction following the recursive description of regular language would prove this.
Common step: The languages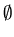 
, {
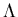} and {a} for any symbol a in 
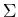are accepted by an FA.
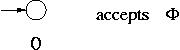
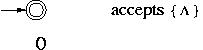
Example:
An NFA-
that accepts the language represented by the regular expression is given - (aa + b)*
Sol: The given regular expression can be constructed using the operation, as below-
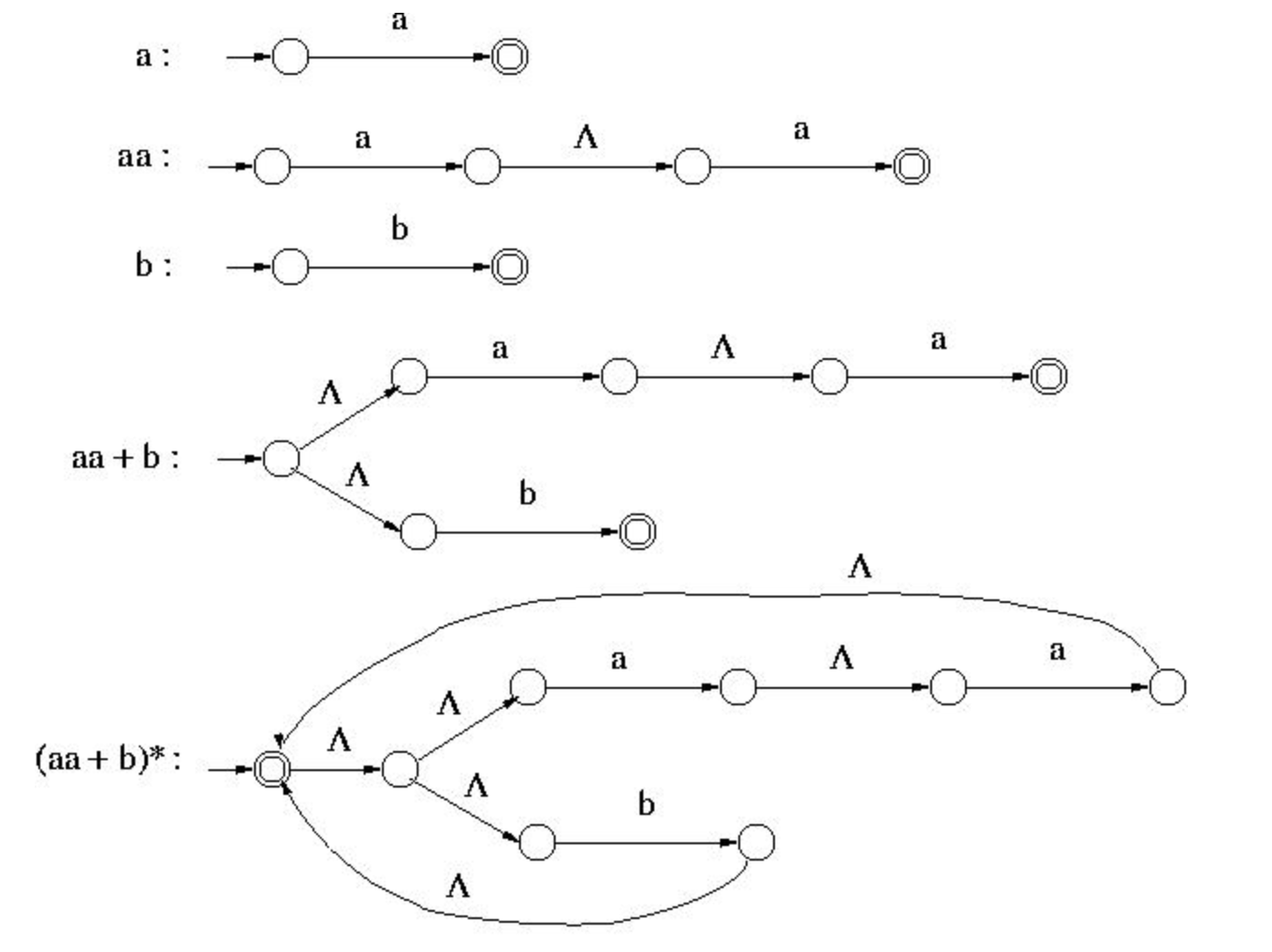
Fig. 2: construction of (aa + b)*
2.4.1 Arden’s theorem
★ The Arden's Theorem is useful both for testing the equivalence of two regular phrases and for converting the DFA to a regular phrase.
★ In the conversion of DFA to a regular expression, let us see its use.
★ There are some algorithms used to build the regular expression form given in the DFA.
1. Let q1 be the initial state.
2. There are q2, q3, q4 .... Qn number of states. The final state may be some qj where j<= n.
3. Let αji represents the transition from qj to qi.
4. Calculate qi such that
qi = αji * qj
If qj is a start state then we have:
qi = αji * qj + ε
5. Similarly, compute the final state which ultimately gives the regular expression 'r'.
2.4.2 Algebraic Method Using Arden’s Theorem
Proof -
R = Q +RP
R = Q + QP* P (Substituting the value of R)
R = Q (ε + P *P)
R = QP * (P * P = P+, P+ + ε = P *)
Sol: With the use of Arden's Theorem, let's solve the given automata
C = Ba
There is a self-loop on input b in state B, a transition from A when input is a, a transition from state C when input is b.
B = Bb + Cb + Aa
In state A, there is a transition from ε (being the start state, transition from ε must be included), a self-loop on input a, a transition from B when input is b.
A = ε + Aa + Bb
Put the value (2) in (1), then
C = Ba
C = (Aa + Bb + Cb) a
C = Aaa + Bba + Cba
Place the value (1) in (2), then
B = Bb + Cb + Aa
B = Aa + Bb + (Ba)b
B = Aa + B (b + ab)
B = Aa(b + ab)* ( using R + QP*)
Place (2) in (3), after that
A = ε +Aa +Bb
A = ε +Aa +Aa (b + ab)*b
A = ε +A(a +a (b + ab)*b)
A = ε + (a +a (b + ab) *b) *
A = (a + a (b + ab) *b)*
Let's combine all the simplified equations with the final state C as a final step.
C = Ba
C = Aa (b + ab) *a
C = (a + a (b + ab)*b) * a (b + ab) * a
● Languages are classified as regular or non-regular.
● Regular languages can be recognized by some DFA.
● There are three ways to prove that a language is not regular.
1. Closure properties of regular languages (unions, intersections, concatenations, “star” operation, etc.)
2. The Pumping Lemma
3. The Myhill-Nerode Theorem and Fooling Sets
● The usefulness of these three depends on the language.
● For some, the closure properties are the easiest to prove non-regularity; for others, it might be the Myhill-Nerode theorem.
● In fact, there are some languages that are not regular, yet are satisfied by the Pumping Lemma! That lemma is not a sufficient condition on non-regularity, so if a language satisfies it, all bets are off as to whether it’s regular or not.
● But if a language “passes” the requirements of Myhill-Nerode, it must be regular.
Regular language consists of all strings with an equal number of zeroes and ones, with the ones following the zeroes. If a DFA recognizes this, it would have to
Compute the total amount of zeroes, followed by the number of ones.
Consequently, an infinite amount of states will be needed. We will use this knowledge combined with the three common ways to prove non-regularity, when we consider this similar language:
B = {0 m 1 n ∣m≠n}
Closure properties of Regular Languages
Regular languages are closed under a wide variety of operations.
Union and intersection –
Pick DFAs recognizing the two languages and use the cross-product construction to build a DFA recognizing their union or intersection.
Set complement –
Pick a DFA recognizing the language, then swap the accept/non-accept markings on its states.
Set difference –
Rewrite set difference using a combination of intersection and set complement
Concatenation and Star –
Pick an NFA recognizing the language and modify it
Homomorphism –
A homomorphism is a function from strings to strings. What makes it a homomorphism is that its output on a multi-character string is just the concatenation of its outputs on each individual character in the string. Or, equivalently, h(xy) = h(x)h(y) for any strings x and y. If S is a set of strings, then h(S) is {w: w = h(x) for some x in S}.
To show that regular languages are closed under homomorphism, choose an arbitrary regular language L and a homomorphism h. It can be represented using a regular expression R. But then h(R) is a regular expression representing h(L). So, h(L) must also be regular.
Notice that regular languages are not closed under the subset/superset relation. For
Example, 0 * 1 * is regular, but its subset {O n 1 n: n > = 0} is not regular, but its subset {01,0011, 000111} is regular again.
The Pigeonhole Theory states that at least one hole must contain two or more pigeons if n pigeons fly into m pigeonholes and n > m
Pigeonhole principle:
A function cannot be one-to-one from a finite set to a smaller set. At least two elements in the domain must have the same image.
Since only a finite number of states can be assumed by a finite state automaton and because there are infinitely many input sequences,
There must be at least one state, according to the pigeonhole principle, to which the automaton returns over and over again. This is an important feature of the
Automaton, then.
Consider a language consisting of 1 and an arbitrary number of 0, followed by 1.
Examples of string inputs include 11,101,1001.
There are now an infinite number of such strings and only a finite number of states.
Therefore, there must be a state sm, by the pigeonhole theory, and two ap and aq input strings with p≠q such that when input to A is either ap or aq, A to state sm. (The pigeons are a's strings, the pigeonholes are the states, and the correspondences equate each string with the state that A goes to when the string is entered)
Example: A language is not regular using the pigeonhole principle, showing that:
L= {s ∑* | s= an bn | n≥ 0}
If we try to find a DFA that recognizes B, we find that so much as it reads the data, the computer needs to remember how many a's have been used. So, with a finite number of states, the machine has to keep track of an infinite number of possibilities. We say in this case that the language B is non-regular
To demonstrate that B is not normal, we use the pigeonhole theory. We use contradictory facts.
Suppose L is regular.
There is then a certain DFA M= (Q, {a,b}, δ, q0, F) for it.
Look now for δ*(q0, ai) for i= 1, 2, ... The pigeonhole theory tells us that there must be some state q, because there are an infinite number of i's, but only a finite number of states in M, q such that:
δ*(q0, an) = q and δ*(q0, am) = q with m≠n
But since M accepts an bn, we must have δ*(q, bn) = qf ∈F.
From this we can conclude that
δ*(q0, ambn) = δ*(δ*(q0, am), bn)
=δ*(q, bn)
=qf
This contradicts the initial assumption that M only accepts ambn if m= n and leads us to believe that it is unlikely for L to be normal.
Key takeaway -
- At least two elements in the domain must have the same image.
- There must be at least one state, according to the pigeonhole principle.
Theorem -
Let L be a regular language. Then a constant c' exists such that for every string w in L
|w| ≥ c
We are able to split w into three strings, w=xyz, so that
● |y| > 0
● |xy| ≤ c
● For all k ≥ 0, the string xyKz is also in L.
2.7.1 Application of Pumping Lemma
It is important to apply Pumping Lemma to show that certain languages are not normal. It can never be used to illustrate the regularity of a language.
● If L is regular, it satisfies Pumping Lemma.
● If L does not satisfy Pumping Lemma, it is non-regular.
Method for demonstrating that a language L is not regular
● We have to assume that L is regular.
● The pumping lemma should hold for L.
● Use the pumping lemma to obtain a contradiction −
● Select w such that |w| ≥ c
● Select y such that |y| ≥ 1
● Select x such that |xy| ≤ c
● Assign the remaining string to z.
● Select k such that the resulting string is not in L.
Therefore, L is not regular.
Example:
Prove that L = {aibi | i ≥ 0} is not regular.
Sol:
● At first, we assume that L is regular and n is the number of states.
● Let w = anbn. Thus |w| = 2n ≥ n.
● By pumping lemma, let w = xyz, where |xy| ≤ n.
● Let x = ap, y = aq, and z = arbn, where p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Thus |y| ≠ 0.
● Let k = 2. Then xy2z = apa2qarbn.
● Number of as = (p + 2q + r) = (p + q + r) + q = n + q
● Hence, xy2z = an+q bn. Since q ≠ 0, xy2z is not of the form anbn.
● Thus, xy2z is not in L.
Hence L is not regular.
2.7.2 Decidability - Decision properties
If the language L of all yes instances to P is decidable, a decision problem P is said to be decidable (i.e., have an algorithm).
Example -
● (DFA acceptance problem) Provided that a DFA accepts a given problem,
Word?
● Given a DFA, does it accept any word? (Emptiness problem for DFA)
● (DFA equivalence issue) Given two DFAs, do they accept the DFA problem?
Language of the same?
Problem: Some of regular L1 and L2 languages, the problem is whether or not there is a string 'w' in both L1 and L2, a deciding problem.
Sol: Firstly, two Turing TM1 and TM2 machines simulate the DFAs of the L1 and L2 languages, respectively. We know a DFA always stops, so a Turing machine that simulates a DFA will always stop, too. In TM1 and TM2 we join the string 'w'. The two Turing machines are going to halt and give us an answer.
We may connect the Turing machine outputs to a modified 'AND' gate that will only output 'yes' when both Turing machines respond to 'yes'. Otherwise, 'no' is production.
This problem is a deciding problem, as this system of two Turing machines and a changed AND gate will always stop.
Regular expressions and finite automata have equivalent expressive power:
For every regular expression R, there is a corresponding FA that accepts the set of strings generated by R.
For every FA A there is a corresponding regular expression that generates the set of strings accepted by A.
The proof is in two parts:
1. An algorithm that, given a regular expression R, produces an FA A such that L(A) == L(R).
2. An algorithm that, given an FA A, produces a regular expression R such that L(R)
== L(A).
Our construction of FA from regular expressions will allow “epsilon transitions” (a transition from one state to another with epsilon as the label). Such a transition is always possible, since epsilon (or the empty string) can be said to exist between any
Two input symbols.
We can show that such epsilon transitions are a notational convenience; for every FA with epsilon transitions there is a corresponding FA without them.
❖ Constructing an FA from an RE
We begin by showing how to construct an FA for the operands in a regular expression.
If the operand is a character c, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and a transition from s0 to sF with label c.
If the operand is epsilon, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and an epsilon transition from s0 to sF.
If the operand is null, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and no transitions.
Given FA for R1 and R2, we now show how to build an FA for R1R2, R1|R2, and R1*.
Let A (with start state a0 and final state aF) be the machine accepting L(R1) and B (with start state b0 and final state bF) be the machine accepting L(R2).
❏ The machine C accepting L(R1R2) includes A and B, with start state a0, final state bF, and an epsilon transition from aF to b0.
❏ The machine C accepting L(R1|R2) includes A and B, with a new start state c0, a new final state cF, and epsilon transitions from c0 to a0 and b0, and from aF and bF to cF.
❏ The machine C accepting L(R1*) includes A, with a new start state c0, a new final state cF, and epsilon transitions from c0 to a0 and cF, and from aF to a0, and from aF to cF.
Regular Expressions in Software Engineering
❏ The usefulness of regular languages in this comes from the fact that regular languages deal in the finite which is true in reference to a computer.
❏ Regular expressions are also used in test case characterizations. These test case characterizations are related to the programs directly, or to the corresponding models for it.
❏ Regular language theory is used to handle paths, and regular expressions are used over the terminals and no terminals of the paths, which are called “regular path expressions.”
❏ A regular expression is sufficient enough to abstractly describe a test case or a class of test cases, but sets of expressions require their own criteria. The use of regular language theory makes it easy for coverage analysis and test set generation.
❏ Regression testing is an important part of the software development cycle. It is a process that is used to determine if a modified program still meets its specifications or if new errors have been found.
Regular Expressions in Lexical Analysis
❏ Lexical analysis is the process of tokenizing a sequence of symbols to eventually parse a string. To perform lexical analysis, two components are required: a scanner and a tokenizer.
❏ A token is simply a block of symbols, also known as a lexeme. The purpose of tokenization is to categorize the lexemes found in a string to sort them by meaning.
❏ For example, the C programming language could contain tokens such as numbers, string constants, characters, identifiers (variable names), keywords, or operators.
❏ The best way to define a token is by a regular expression. Scanning process can be quite complex and may require more than one pass to complete.
❏ Backtracking is rereading an earlier part of a string to see if it matches a regular expression based on some information that could only be obtained by analyzing a later part of the string.
❏ For example, to determine if a lexeme is a valid identifier in C, we could use the following regular expression:
[a-zA-Z] [a-zA-Z 0-9] ∗
This regular expression says that identifiers must begin with a Roman letter or an underscore and may be followed by any number of letters, underscores, or numbers.
● Regular languages are referred to as the languages recognized by certain regular expressions.
● For matching character combinations in strings, regular expressions are used. This pattern is used by the string search algorithm to locate operations on a string.
● A regular expression may also be defined as a pattern sequence that defines a series.
Support all strings beginning with, where ∑ = {0, 1}
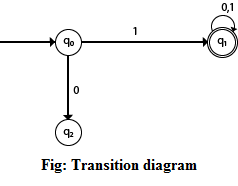
Using a transition graph, finite automata can be represented. The machine is initially in the starting state q0 in the above diagram, then the machine changes its state to q1 on obtaining input 1.
The computer changes its state to q2 from q0 on obtaining 0, which is the dead state. The computer changes its state to q1, which is the final state, from q1 on obtaining input 0. 1. 10, 11, 110, 101, 111....... Are the possible input strings that can be created, indicating that all strings begin with 1.
References:
1.Introduction to Automata Theory, Languages, and Computation, 2e by John E, Hopcroft, Rajeev Motwani, Jeffery D. Ullman, Pearson Education.
2.Theory of Computer Science (Automata, Languages and Computation), 2e by K. L. P. Mishra and N. Chandrasekharan, PHI
3.Harry R. Lewis and Christos H. Papadimitriou, Elements of the Theory of Computation, Pearson Education Asia.
