Unit – 3

Regular and Non-Regular Grammar

3.1 Context free Grammar (CFG)

3.1.1 Definition

Context-free grammar (CFG) is a collection of rules (or productions) for recursive rewriting used to produce string patterns.

It consists of:

❏      a set of terminal symbols,

❏      a set of non-terminal symbols,

❏      a set of productions,

❏      a start symbol.

Context-free grammar G can be defined as:

G = (V, T, P, S)

Where 

G - grammar, used for generate string,

V - final set of non-terminal symbol, which are denoted by capital letters,

T - final set of terminal symbols, which are denoted be small letters,

P - set of production rules, it is used for replacing non terminal symbol of a string in both side (left or right)

S - start symbol, which is used for derive the string

A CFG for Arithmetic Expressions -

An example grammar that generates strings representing arithmetic expressions with the four operators +, -, *, /, and numbers as operands is:

1. <expression> --> number

2. <expression> --> (<expression>)

3.<expression> --> <expression> +<expression>

4. <expression> --> <expression> - <expression>

5. <expression> --> <expression> * <expression>

6. <expression> --> <expression> / <expression>

The only non-terminal symbol in this grammar is <expression>, which is also the

Start symbol. The terminal symbols are {+, -, *, /, (, ), number}

❏      The first rule states that an <expression> can be rewritten as a number.

❏      The second rule says that an <expression> enclosed in parentheses is also an <expression>

❏      The remaining rules say that the sum, difference, product, or division of two <expression> is also an expression.

3.1.2 Derivations

Derivation is the collection of rules for development. Via these production laws, it is used to get the input string. We have to take two decisions during parsing.

These are as follows:

We have two options to decide which non-terminal to be placed with production rule

1. Leftmost Derivation:

The input is scanned and replaced by the production rule from left to right in the left-most derivation. So, we read the input string from left to right in the left-most derivation.

Example:

➢      Produle rule -

P = P + P

P = P - P

P = a | b

➢      Input -

a - b + a

➢      Leftmost derivation is:

P = P + P 

P = P - P + P

P = a - P + P

P = a - b + P 

P = a - b + a

2.     Rightmost Derivation:

The input is scanned and replaced by the production rule from right to left in the right-most derivation. So, we read the input string from right to left in the right-most derivation.

Example:

➢      Produle rule -

P = P + P

P = P - P

P = a | b

➢      Input -

a - b + a

➢      Rightmost Derivation is -

P = P - P 

P = P - P + P 

P = P - P + a 

P = P - b + a 

P = a - b + a 

★      We can receive the same string when we use the leftmost derivation or rightmost derivation.

Note -

The reception of a string does not affect this method of derivation.

3.1.3 Languages

●      A context-free language (CFL) is a language developed by context-free grammar (CFG) in formal language theory. In programming languages, context-free languages have many applications, particularly most arithmetic expressions are created by context-free grammars.

●      Through comparing different grammars that characterize the language, intrinsic properties of the language can be separated from extrinsic properties of a particular grammar.

●      In the parsing stage, CFLs are used by the compiler as they describe the syntax of a programming language and are used by several editors.

A grammatical description of a language has four essential components -

1. There is a set of symbols that form the strings of the language being defined. They are called terminal symbols, represented by V t .

II.            There is a finite set of variables, called non-terminals. These are represented by V n.

III.            One of the variables represents the language being defined; it is called the start symbol. It is represented by S.

IV.            There are finite set of rules called productions that represent the recursive definition of a language. Each production consists of:

1. A variable that is being defined by the production. This variable is also called the production head.
2. The production symbol ->
3. A string of zero terminals and variables, or more.

3.1.4 Derivation Trees and Ambiguity

The tree of derivation is a graphical representation of the derivation for a given CFG of the development rules given. It is the easy way to explain how to extract any string from a given set of production rules to obtain the derivation.

The parse tree follows the operators' precedence. The deepest sub-tree went through first. So, the operator has less precedence over the operator in the sub-tree in the parent node.

A parse tree contains the following properties:

1. The root node is always a node indicating start symbols.
2. The derivation is read from left to right.
3. The leaf node is always terminal nodes.
4. The interior nodes are always the non-terminal nodes.

Example:

Production rule:

1. P = P + P 
2. P = P * P 
3. P = a | b | c

Input:

a * b + c 

Step 1 -   

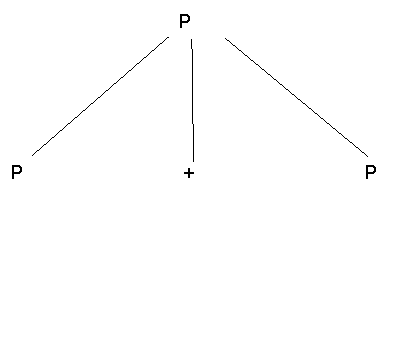
Step 2 -

Step 3 -

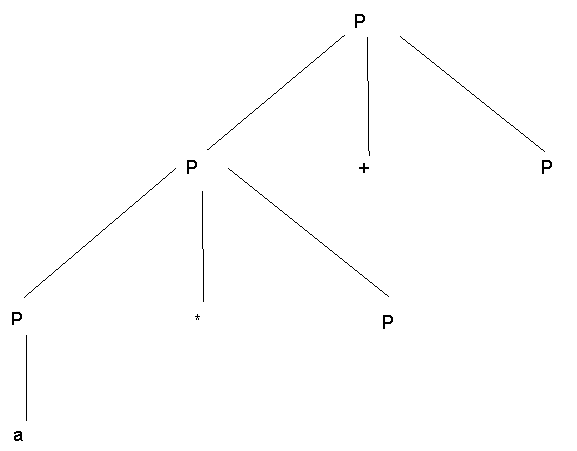
Step 4 -

Step 5 -

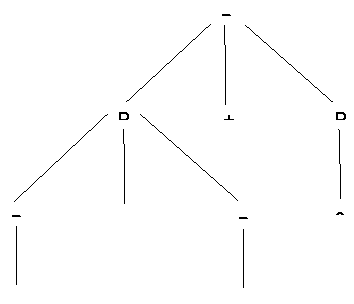
Ambiguous Context Free Languages:

If there is no unambiguous grammar to describe the language and it is often called necessarily ambiguous Context Free Languages, a context free language is called ambiguous.

Key takeaways:

❖      Language generated by grammar L(G) may or may not be ambiguous if a context-free grammar G is ambiguous.

❖      Ambiguous CFG will not always be translated to unambiguous CFG. It is possible to convert just some ambiguous CFG to unambiguous CFG.

❖      There is no algorithm to convert ambiguous CFG to unambiguous CFG.

❖      There always exists an unambiguous CFG corresponding to unambiguous CFL.

❖      Deterministic CFL are always unambiguous.

3.2 Regular grammars

If it has rules of form A -> an or A -> aB or A -> ⁇ where ⁇ is a special symbol called NULL, grammar is natural. Standard grammar is formal grammar, i.e. regular right or regular left. Regular language is defined in every periodic grammar

3.2.1 Right linear grammar

Right linear grammar is also called right regular grammar is a formal grammar N, Σ, P, S such that all the production rules in P are of one of the following forms:

1. A → a, where A is a non-terminal in N and a is a terminal in Σ.
2. A → aB, where A and B are non-terminals in N and a is in Σ
3. A → ε, where A is in N and ε denotes the empty string, i.e. the string of length 0.

3.2.2 Left linear grammar

Left linear grammar is also called left regular grammar. There are some rules to follow:

1. A → a, where A in N is a non-terminal and an in Σ is a terminal.
2. A → Ba, where A and B in N are non-terminals and an in Σ is
3. A → ε, where A is N and ε denotes the empty string, i.e. the longitudinal string 0.

3.3 Conversion of FA into CFG and Regular grammar into FA

Conversion from regular grammar into FA

We are using the SubSet method to convert regular grammar into FA. Basically, this process is used to obtain FA from any given regular expression. Some methods are as:

Step 1: Build a transition diagram, using NFA with ε moves, for a given regular expression.

Step 2: Transform this NFA to a non-ε NFA with ε.

Step 3: The received NFA is transformed to an analogous DFA.

Example:

Design the FA for regular expression 10 + (0 + 11)0* 1.

Sol: The first move is to construct the transition diagram for given regular expression.

Step 1:

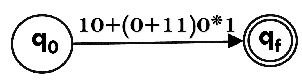
Step 2:

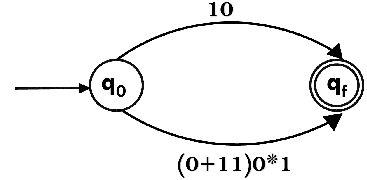
Step 3:

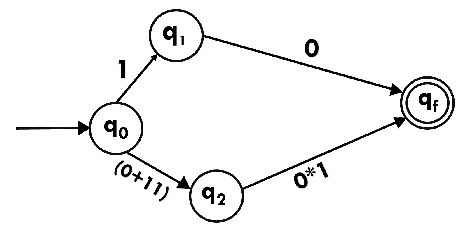
Step 4:

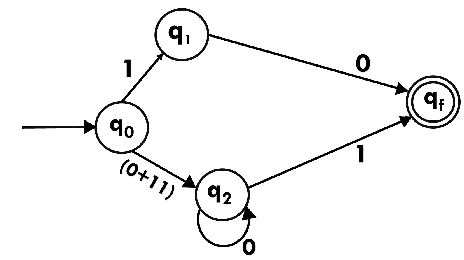
Step 5:

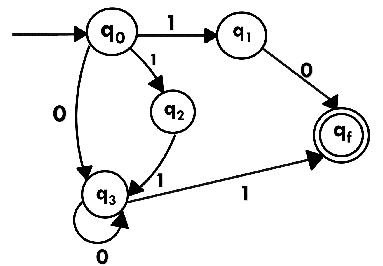
We've got an NFA now without ε. We're going to translate it into the necessary DFA for that now and we're going to write a transition table for this NFA first.

The equivalent DFA transition table is:

Example:

Construct a CFG for a language L = {wcwR | where w € (a, b)*}.

Solution:

For a given language, the string that can be generated is {aacaa, bcb, abcba, bacab, abbcbba, ....}

The grammar could be:

1. S → aSa     rule 1 
2. S → bSb     rule 2 
3. S → c       rule 3 

Now if we want to derive a string "abbcbba", we can start with start symbols.

1. S → aSa  
2. S → abSba       from rule 2 
3. S → abbSbba     from rule 2 
4. S → abbcbba     from rule 3 

It is therefore possible to derive some of this kind of string from the production rules given.

3.4 Simplification of CFG

As we have included a context-free grammar can effectively represent different languages. Not all grammar is always optimized, which means that there might be some extra symbols in the grammar (non-terminal). Unnecessary change in the length of grammar with additional symbols.

Here are the properties of reduced grammar:

1. Every parameter (i.e. non-terminal) and every terminal of G occurs in the derivation of any word in L.
2. As X→Y where X and Y are non-terminal, there should not be any output.
3. If ε is not in the L language, then the X→ ε output does not have to be.

Let’s see the simplification process

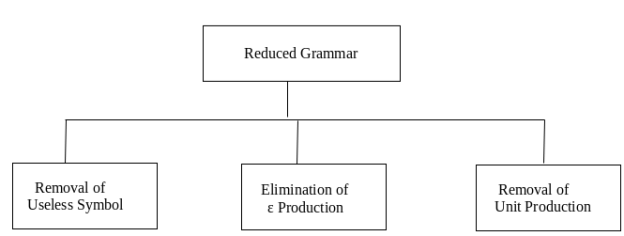
Fig.: Simplification process

Step 1: First find out all nullable non-terminal variables which derive ε.

Step 2: Create all output A → x for each production A →a where x is extracted from a by removing one or more non-terminals from step 1.

Step 3: Now combine with the original output the outcome of step 2 and delete ε productions.

Example:  Remove the production from the given CFG

1. E → XYX 
2. X → 0X | ε 
3. Y → 1Y | ε

Solution:

Now, we remove the rules X → ε and Y → ε while removing ε production. In order to maintain the sense of CFG, whenever X and Y appear, we actually position ε on the right-hand side.

Let’s see

If the 1st X at right side is ε, then

E → YX

Similarly, if the last X in right hand side is ε, then

E → XY

If Y = ε, then

E → XX

If Y and X are ε then,

S → X

If both X are replaced by ε

E → Y 

Now,

E → XY | YX | XX | X | Y

Now let us consider

X → 0X 

If we then put ε for X on the right-hand side,

X → 0

X → 0X | 0 

Similarly, Y → 1Y | 1

Collectively, with the ε output excluded, we can rewrite the CFG as

E → XY | YX | XX | X | Y 

X → 0X | 0 

Y → 1Y | 1

To remove production unit, follow given steps: →

Step 1: To delete X → Y, when Y→ a occurs in the grammar, apply output X → a to the grammar law.

Step 2: Remove X → Y from the grammar now.

Step 3: Repeat steps 1 and 2 until all unit output is deleted.

Example:

1. E → 0X | 1Y | Z 
2. X → 0E | 00 
3. Y → 1 | X 
4. Z → 01

Sol:

E → Z is a unit production. But while removing E → Z, we have to consider what Z gives. So, we can add a rule to E.

E → 0X | 1Y | 01 

Similarly, Y → X is also a unit production so we can modify it as

Y → 1 | 0S | 00 

Finally, then without unit manufacturing, we can write CFG as

E → 0X | 1Y | 01 

X → 0E | 00 

Y → 1 | 0S | 00 

Z → 01 

Key takeaways:

-         Grammar simplification means reducing grammar by the elimination of useless symbols.

-         Simplification process contains three major parts.

-         Removal of useless symbol, Elimination of ε production, Removing unit production

3.5 Normal Forms

3.5.1 Chomsky Normal Form (CNF)

The Chomsky normal form (CNF) is a context free grammar (CFG) if all output rules satisfy one of the conditions below:

Consider the following grammars,

G1 = {S->a, S->AZ, A->; a, Z->z}

G2 = {S->a, S->aZ, Z->a}

As production rules comply with the rules defined for CNF, the grammar G1 is in CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains terminal followed by non-terminal which does not satisfy the rules specified for CNF.

Key takeaway –

3.5.2 Greibach Normal Form (GNF)

If the productions are in the following forms, a CFG is in the Greibach Normal Form -

A → b

A → bD 1 …D n

S → ε

Where A, D 1, ...., D n are non-terminals and b is a terminal.

Algorithm to Convert a CFG into Greibach Normal Form

Step 1 − If the starting symbol S is on the right side, create a new starting symbol.

S 'symbol and a new S'→ S output.

Step 2 − Remove Null productions.

Step 3 − Remove unit productions.

Step 4 − Delete both left-recursion direct and indirect.

Step 5 − To transform it into the proper form of GNF, make proper output substitutions.

Example:

Convert the following CFG into CNF

S → XY | Xn | p

X → mX | m

Y → Xn | o

Sol:

Here, S does not appear on the right side of any production and in the production rule collection, there is no unit or null output. So, we'll be able to bypass step 1 to step 3.

Step 4 -Now after replacing

X in S → XY | Xo | p

With

MX | m

We obtain

S → mXY | mY | mXo | mo | p.

And after replacing

X in Y → X n | o

With the right side of

X → mX | m

We obtain

Y → mXn | mn | o.

The production set is added to two new productions O → o and P → p and then we arrived at the final GNF as the following -

S → mXY | mY | mXC | mC | p

X → mX | m

Y → mXD | mD | o

O → o

P → p

3.5.3 Chomsky Hierarchy

The Chomsky Hierarchy describes the class of languages that the various machines embrace. The language group in Chomsky's Hierarchy is as follows:

1. Type 0 known as Unrestricted Grammar.
2. Type 1 known as Context Sensitive Grammar.
3. Type 2 known as Context Free Grammar.
4. Type 3 Regular Grammar.

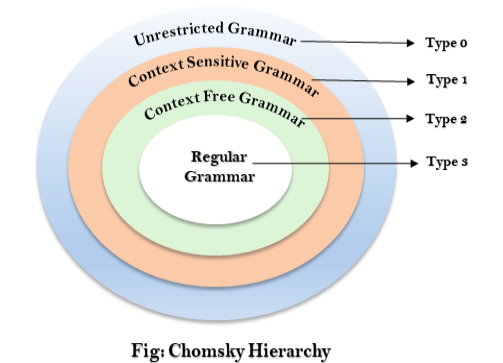
The above diagram shows the hierarchy of Chomsky. Each language of type 3 is therefore also of type 2, 1 and 0 respectively. Similarly, every language of type 2 is also of type 1 and type 0 likewise.

➢      Type 0 grammar -

Type 0 grammar is known as Unrestricted grammar. The grammar rules of these types of languages are unregulated. Turing machines can model these languages efficiently.

Example:

1. BAa → aa 
2. P → p  

➢      Type 1 grammar -

Type 1 grammar is known as Context Sensitive Grammar. Context-sensitive grammar is used to describe language that is sensitive to context. The context-sensitive grammar follows the rules below:

Key note - Where the number of symbols in V is equal to or less than T

Example:

1. S → AT 
2. T → xy 
3. A → a

➢      Type 2 grammar -

Type 2 Grammar is called Context Free Grammar. Context free languages are the languages which can be represented by the CNF (context free grammar) Type 2 should be type 1. The production rule is:

A → α

Key note: Where A is any single non-terminal and is any combination of terminals and non-terminals.

Example:

1. A → aBb 
2. A → b 
3. B → a  

➢      Type 3 grammar -

Type 3 Grammar is called Regular Grammar. Those languages that can be represented using regular expressions are regular languages. These languages may be NFA or DFA-modelled.

Type3 has to be in the form of -

V → T*V / T*

Example:

A → xy  

Note -

The most limited form of grammar is Type3. Type2 and Type1 should be the grammar of Type3.

3.6 Programming problems based on the properties of CFGs

Problem - Find a reduced grammar similar to grammar G, having rules of output

P: S AC | B, A → a, C → c | BC, E   → aA | e

Sol: Stage 1:

T = {a, c, e}

W1 = {A, C, E} from rules A a, C c and E aA

W2 = {A, C, E} U {S} from rule S AC

W3 = {A, C, E, S} U

After W2 = W3, we can obtain 

G’ as: G’ = {{A, C, E, S}, {a, c, e}, P, {S}}

Where P: S → AC, A → a, C → c, E → aA | e

Stage 2:

Y1 = {S}

Y2 = {S, A, C} from rule S AC

Y3 = {S, A, C, a, c} from rules A a and C c

Y4 = {S, A, C, a, c}

After Y3 = Y4, we can obtain

G” as: G” = {{A, C, S}, {a, c}, P, {S}}

Where P: S → AC, A → a, C → c

Problem - Adjust the output of units from the following:

S → XY, X → a, Y → Z | b, Z → M, M → N, N → a

Sol:

In the grammar, there are 3 unit productions:

Y → Z, Z → M, and M → N

Now, we will delete M → N

As N → a, we add M → a, and M → N is omitted.

It becomes the output unit

S → XY, X → a, Y → Z | b, Z → M, M → a, N → a

Next, we will delete Z → M

As M → a, we add Z→ a, and Z → M is omitted.

It becomes the output unit

S → XY, X → a, Y → Z | b, Z → a, M → a, N → a

Next, we will delete Y → Z

As Z → a, we add Y→ a, and Y → Z is omitted.

It becomes the output unit

S → XY, X → a, Y → a | b, Z → a, M → a, N → a

Z, M, and N are difficult to achieve now, so we can erase them.

Unit output release is the final CFG:

S → XY, X → a, Y → a | b

References:

1. Harry R. Lewis and Christos H. Papadimitriou, Elements of the Theory of Computation, Pearson Education Asia.

2.     Introduction to Automata Theory, Languages, and Computation, 2e by

John E, Hopcroft, Rajeev Motwani, Jeffery D. Ullman, Pearson Education.