Unit – 4
Push Down Automata and Properties of Context Free Languages
Pushdown Automata -
It is a way to implement a context-free grammar as we design DFA for a regular grammar. A DFA can remember a finite amount of information, but a PDA can remember an infinite amount of information.
Basically, a pushdown automaton is -
“Finite state machine” + “a stack”
A pushdown automaton has three components −
● an input tape,
● a control unit, and
● a stack with infinite size.
The stack head scans the top symbol of the stack.
A stack does two operations −
● Push − a new symbol is added at the top.
● Pop − the top symbol is read and removed.
A PDA may or may not read an input symbol, but it has to read the top of the stack in every transition.
Fig. 1: Basic structure of PDA
A PDA can be formally described as a 7-tuple (Q, ∑, S, δ, q0, I, F) −
Where,
● Q is the finite number of states
● ∑ is input alphabet
● S is stack symbols
● δ is the transition function: Q × (∑ ∪ {ε}) × S × Q × S*)
● q0 is the initial state (q0 ∈ Q)
● I is the initial stack top symbol (I ∈ S)
● F is a set of accepting states (F ∈ Q)
The following diagram shows a transition in a PDA from a state q1 to state q2, labeled as a,b → c −
Fig. 2: Example
This means at state q1, if we encounter an input string ‘a’ and the top symbol of the stack is ‘b’, then we pop ‘b’, push ‘c’ on top of the stack and move to state q2.
4.1.1 Definition
Non - deterministic Pushdown Automata -
● Non-deterministic pushdown automata are quite similar to the NFA.
● Non-deterministic PDAs are also approved by the CFG that accepts deterministic PDAs.
● Similarly, there are several CFGs that only NPDA and not DPDA can consider. Therefore, NPDA is more efficient than DPDA.
● Non deterministic pushdown automata is basically a nonfinite automata (nfa) with a stack added to it.
Nondeterministic pushdown automaton or npda is a 7-tuple -
M = (Q, ∑, T, δ, q0, z, F)
Where
● Q is a finite set of states,
● ∑ is the input alphabet,
● T is the stack alphabet,
● δ is a transition function,
● q0 ∈ Q is the initial state,
● z ∈ T is the stack start symbol, and
● F ⊆ Q is a set of final states.
4.1.2 Moves
The three groups of loop transitions in state q represent these respective functions:
● input a with no b’s on the stack: push a
● input b with no a’; s on the stack: push b
● input a with b’s on the stack: pop b; or, input b with a’s on the stack: pop a
For example, if we have seen 5 b’s and 3 a’s in any order, then the stack should be “bbc”. The transition to the final state represents the only non-determinism in the PDA in that it must guess when the input is empty in order to pop off the stack bottom.
4.1.3 A Language accepted by NPDA
The language is L = {w∈ {a,b}* : w = a n b n , n ≥ 0 }. Here are two PDAs for L:
Fig. 3: PDA for L
The idea in both of these machines is to stack the a's and match off the b's. The first one is non-deterministic in the sense that it could prematurely guess that the a’s are done and start matching off b’s. The second version is deterministic in that the first b acts as a trigger to start matching off. Note that we have to make both states final in the second version in order to accept ε.
The equal a’s and b’s language -
#σ(w) = the number of occurrences of σ in w
The language is L = {w ∈ {a,b}*: #a(w) = #b(w) }. Here is the PDA:
Fig. 4: PDA for Language
As you can see, most of the activity surrounds the behavior in state q. The idea is to have the stack maintain the excess of one symbol over the other. In order to achieve our goal, we must know when the stack is empty.
Empty Stack Knowledge
There is no mechanism built into a PDA to determine whether the stack is empty or not.
It’s important to realize that the transition:
Fig. 5: Transition
Means to do so without consulting the stack; it says nothing about whether the stack is empty or not.
Nevertheless, one can maintain knowledge of an empty stack by using a dedicated stack symbol, c, representing the “stack bottom” with the property that it is pushed onto an empty stack by a transition from the start state with no other outgoing or incoming transitions.
Key takeaways -
- Basically, nondeterministic pushdown automatics are a non-finite automatic with a stack attached to it.
- A DFA can remember a finite amount of data, but a PDA can remember a finite amount of details.
4.2.1 Deterministic Pushdown Automata (DPDA)
● Machine transitions are based on the actual state and input symbol, as well as the stack's current uppermost symbol.
● The lower symbols in the stack are not apparent and do not have an immediate effect.
● The acts of the computer include pushing, popping or replacing the top of the stack.
● For the same combination of input symbol, state, and top stack symbol, a deterministic pushdown automaton has at most one legal transformation.
● This is where the pushdown automaton varies from the nondeterministic one.
● DPDA is a subset of context free language.
A deterministic pushdown automata M can be defined as 7 tuples -
M = (Q, ∑, T, q0, Z0, A, δ)
Where,
● Q is finite set of states,
● ∑ is finite set of input symbol,
● T is a finite set of stack symbol,
● q0 ∈ Q is a start state,
● Z0 ∈ T is the starting stack symbol,
● A ⊆ Q, where A is a set of accepting states,
● δ is a transition function, where:
δ :(Q X (∑ U {ε}) X T) ➝ p(Q X T* )
4.2.2 Deterministic Context free Language (DCFL)
A number of deterministic language outcomes (languages accepted by pushdown automata without choice of moves) are generated. Specially
● Any deterministic language is unambiguous.
● A deterministic language is the complement of each deterministic language.
● A variety of concerns are shown to be recursively insoluble
● Several operations are obtained that preserve deterministic languages (for example, intersection with a regular set).
Key takeaways -
- Deterministic PDA is a subset of context free language.
- A number of deterministic language outcomes are generated by pushdown automatons
The non-deterministic pushdown automatic is very similar to the NFA.
Non-deterministic PDAs are also approved by the CFG that accepts deterministic PDAs. Similarly, there are some CFGs which can be accepted only by NPDA and not by DPDA. Therefore, NPDA is more efficient than DPDA.
Example:
Design PDA for Palindrome strips.
Solution:
Suppose the language consists of string L = {aba, aa, bb, bab, bbabb, aabaa, ......].
The string can also be odd palindrome or even palindrome. The logic for building PDA is that we will push a symbol until half of the string onto the stack, then we will read each symbol and then perform the pop operation. To see whether the symbol that is popped is similar to the symbol that is read, we will compare. We expect the stack to be empty if we reach the end of the input.
This PDA is a non-deterministic PDA because the middle of the given string is based and reading the string from left and matching it with from right (reverse) direction leads to non-deterministic moves. Here is the ID
- δ(q1, a, Z) = (q1, aZ)
- δ(q0, b, Z) = (q1,bZ)
- δ(q0, a, a) = (q1,aa)
- δ(q1, a, b) = (q1, ab)
- δ(q1, a, b) = (q1, ba)
- δ(q1, b, b) = (q1, bb)
(pushing the symbol onto the stack)
7. δ(q1, a, a) = (q2, ε)
8. δ(q1, b, b) = (q2, ε)
9. δ(q2, a, a) = (q2, ε)
10. δ(q2, b, b) = (q2, ε)
11. δ(q2, ε, Z) = (q2, ε)
(popping the symbol on reading the same kind of symbol)
Simulation of abaaba
- δ(q1, abaaba, Z) Apply rule 1
- ⊢ δ(q1, baaba, aZ) Apply rule 5
- ⊢ δ(q1, aaba, baZ) Apply rule 4
- ⊢ δ(q1, aba, abaZ) Apply rule 7
- ⊢ δ(q2, ba, baZ) Apply rule 8
- ⊢ δ(q2, a, aZ) Apply rule 7
- ⊢ δ(q2, ε, Z) Apply rule 11
- ⊢ δ(q2, ε) Accept
We may construct an equivalent non-deterministic PDA if a grammar G is context-free, which accepts the language generated by the context-free grammar G. For Grammar G, a parser can be constructed.
When P is a pushdown automaton, and G is context free grammar can be constructed, where
L(G) = L(P)
Algorithm to find PDA corresponding to a given CFG
Input − A CFG, G = (V, T, P, S)
Output − Equivalent PDA, P = (Q, ∑, S, δ, q0, I, F)
Step 1 − Convert the productions of the CFG into GNF.
Step 2 − The PDA will have only one state {q}.
Step 3 − The start symbol of CFG will be the start symbol in the PDA.
Step 4 − All non-terminals of the CFG will be the stack symbols of the PDA and all the terminals of the CFG will be the input symbols of the PDA.
Step 5 − For each production in the form A → aX where a is terminal and A, X are combination of terminal and non-terminals, make a transition δ (q, a, A)
A computational model based on the generalization of Pushdown Automata (PDA) is the Two-Stack PDA.
A deterministic two-stack PDA is equal to a non-deterministic two-stack PDA.
The move of the Two-Stack PDA is based on
● The state of the finite control.
● The input symbol read.
● The top stack symbol on each of its stacks.
A Turing machine can accept languages with one stack not recognized by any PDA.
The strength of pushdown automata can be increased by adding additional (extra) stacks.
A PDA with two stacks actually has the same computing power as a Turing Machine.
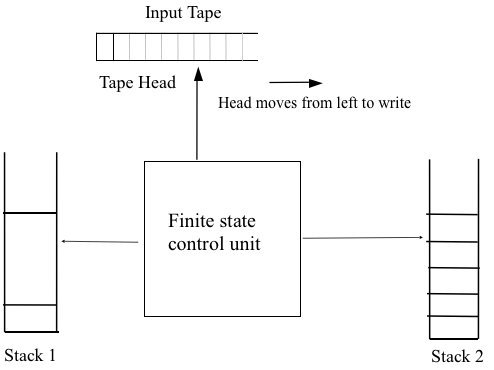
Fig 6: Two stack PDA
Lemma: The language L = {anbncn | n>=1} is not context free.
Proof (By contradiction)
Assuming that this language is context-free; hence it will have a context-free
Grammar.
Let K be the constant of the Pumping Lemma.
Provided the aKbKcK series, where L is greater than K in duration.
By the Pumping Lemma this is represented as uvxyz, such that all uvixyiz are also in, which is not possible, as: either v or y cannot contain many letters from {a,b,c} ; else they are in the wrong order .
If v or y consists of ‘a’s, ‘b’s or ‘c’s, then uv2xy2z cannot maintain the balance amongst the three letters.
Lemma: The language L = {aibjck | i < j and i < k} is not context free.
Proof (By contradiction)
Assuming that this language is context-free; hence it will have a context-free grammar.
Let K be the Pumping Lemma constant.
Considering the string aKbK+1cK+1, which is L > K.
By the Pumping Lemma this must be represented as uvxyz, such that all uvixyiz are also in L.
-As mentioned previously neither v nor y may contain a mixture of symbols.
-Suppose consists of ‘a’s.
Then there is no way y cannot have ‘b’s and ‘c’s. It generates enough letters to keep
Them more than that of the ‘a’s (it can do it for one or the other of them, not both).
Similarly, y cannot consist of just ‘a’s.
So, suppose then that v or y contains only ‘b’s or only ‘c’s.
Consider the uv0xy0z string that must be in L. Since both v and y have been dropped, we must have at least one 'b' or one 'c' less than we had in uvxyz, which
It was akbk+1ck+1. Consequently, to be a member of L, this string no longer has enough of either 'b's or' c's.
They are closed under −
❖ Union
❖ Concatenation
❖ Kleene Star operation
Union
Let A1 and A2 be two context free languages. Then A1 ∪ A2 is also context free.
Example
Let A1 = {xn yn, n ≥ 0}. Corresponding grammar G 1 will have P: S1 → aAb|ab
Let A2 = {cm dm, m ≥ 0}. Corresponding grammar G 2 will have P: S2 → cBb| ε
Union of A1 and A2, A = A1 ∪ A2 = {xn yn} ∪ {cm dm}
The corresponding grammar G will have the additional production S → S1 | S2
Note - So under Union, CFLs are closed.
Concatenation
If A1 and A2 are context free languages, then A1 A2 is also context free.
Example
Union of the languages A1 and A2, A = A1 A2 = {anbncmdm}
The additional development would have the corresponding grammar G, P: S → S1 S2
Note - So under Concatenation, CFL are locked.
Kleene Star
If A is a context free language, so that A* is context free as well.
Example
Let A = {xn yn, n ≥ 0}. G will have corresponding grammar P: S → aAb| ε
Kleene Star L1 = { xn yn}*
The corresponding grammar G1 will have additional productions S1 → SS 1 | ε
Note - So under Kleene Closure, CFL's are closed.
Context-free languages are not closed under −
● Intersection − If A1 and A2 are context free languages, then A1 ∩ A2 is not necessarily context free.
● Intersection with Regular Language − If A1 is a regular language and A2 is a context free language, then A1 ∩ A2 is a context free language.
● Complement − If A1 is a context free language, then A1’ may not be context free.
Lemma: Whether a context-free language is empty or not is determinable.
Proof:
We need to show that a string can be generated by the corresponding context-free grammar.
If a string can be generated by a CFG, it should be able to do so without recursion (since we could just skip the recursion and generate a shorter string). If there are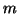 
non-terminals altogether, then a tree less than 
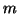in height must have leaves that are only terminals.
To see if the CFG generates a sentence thus we need only examine all such trees
Therefore, we only need to analyse all such trees to see if a sentence is created by the CFG.
Some decision problems for CFGs (and push-down automata accordingly) are not solvable.
We state, without proof, that the following problems in general are undecidable:
● Given two context-free languages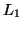 
and 
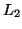, is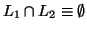 
?
ie. Is the same string generated by two context-free grammars?
● Provided any terminal symbol Σ alphabet, can a grammar produce all the strings of this alphabet Σ*?
● Is the context-free grammar for a language ambiguous?
● Given two context-free languages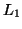 
and 
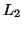, is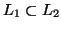 
?
● Given two context-free languages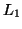 
and 
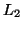, is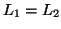 
?
Example - – Let us convert CFG to CNF.
S → ASB
A →aAS|a|ε
B →SbS|A|bb
Sol: Step 1. As start symbol S appears on the RHS, we will create a new production rule S0->S. Therefore, the grammar will become:
S0->S
S → ASB
A →aAS|a|ε
B →SbS|A|bb
Step 2. As grammar contains null production A->ε, its removal from the grammar
Yields:
S0->S
S → ASB|SB
A →aAS|aS|a
B →SbS| A|ε|bb
Now, it creates null production B→ε, its removal from the grammar yields:
S0->S
S → AS|ASB| SB| S
A →aAS|aS|a
B →SbS| A|bb
Now, it creates unit production B->A, its removal from the grammar yields:
S0->S
S → AS|ASB| SB| S
A →aAS|aS|a
B →SbS|bb|aAS|aS|a
Also, removal of unit production S0->S from grammar yields:
S0->AS|ASB| SB| S
S → AS|ASB| SB| S
A →aAS|aS|a
B →SbS|bb|aAS|aS|a
Also, removal of unit production S->S and S0->S from grammar yields:
S0-> AS|ASB| SB
S → AS|ASB| SB
A →aAS|aS|a
B →SbS|bb|aAS|aS|a
Step 3. In production rule A->aAS |aS and B->SbS|aAS|aS, terminals a and b exist
On RHS with non-terminates. Removing them from RHS:
S0-> AS|ASB| SB
S → AS|ASB| SB
A →XAS|XS|a
B →SYS|bb|XAS|XS|a
X →a
Y→b
Also, B->bb can’t be part of CNF, removing it from grammar yields:
S0-> AS|ASB| SB
S → AS|ASB| SB
A →XAS|XS|a
B →SYS|VV|XAS|XS|a
X → a
Y → b
V → b
Step 4: In production rule S0->ASB, RHS has more than two symbols, removing it
From grammar yields:
S0-> AS|PB| SB
S → AS|ASB| SB
A →XAS|XS|a
B →SYS|VV|XAS|XS|a
X → a
Y → b
V → b
P → AS
Similarly, S->ASB has more than two symbols, removing it from grammar yields:
S0-> AS|PB| SB
S → AS|QB| SB
A →XAS|XS|a
B →SYS|VV|XAS|XS|a
X → a
Y → b
V → b
P → AS
Q → AS
Similarly, A->XAS has more than two symbols, removing it from grammar yields:
S0-> AS|PB| SB
S → AS|QB| SB
A →RS|XS|a
B →SYS|VV|XAS|XS|a
X → a
Y → b
V → b
P → AS
Q → AS
R → XA
Similarly, B->SYS has more than two symbols, removing it from grammar yields:
S0 -> AS|PB| SB
S → AS|QB| SB
A →RS|XS|a
B →TS|VV|XAS|XS|a
X → a
Y → b
V → b
P → AS
Q → AS
R → XA
T → SY
Similarly, B->XAX has more than two symbols, removing it from grammar yields:
S0-> AS|PB| SB
S → AS|QB| SB
A →RS|XS|a
B →TS|VV|US|XS|a
X → a
Y → b
V → b
P → AS
Q → AS
R → XA
T → SY
U → XA
So, this is the required CNF for given grammar.
References:
1. Introduction to Automata Theory, Languages, and Computation, 2e by John E, Hopcroft, Rajeev Motwani, Jeffery D. Ullman, Pearson Education.
2. Theory of Computer Science (Automata, Languages and Computation), 2e by K. L. P. Mishra and N. Chandrasekharan, PHI
3. Harry R. Lewis and Christos H. Papadimitriou, Elements of the Theory of Computation, Pearson Education Asia.
