Unit – 5

Turing Machines and Recursive Function Theory

5.1 Basic Turing Machine Model

An information processing system is associate acceptive device that accepts the languages (recursively calculable set) generated by sort zero grammars. It had been fancied in 1936 by Alan Turing.

5.1.1 Representation of Turing Machines

An information processing system (TM) may be a mathematical model that consists of

Associate infinite length tape divided into cells on which input is given. It consists of a head that reads the input tape.

A state register stores the state of the information processing system. Once reading an associated input image, it’s replaced with another image, its internal state is modified, and it moves from one cell to the proper or left. If the metal reaches the ultimate state, the input string is accepted, otherwise rejected.

A metal will be formally delineated as a 7-tuple (Q, X, ∑, δ, q0, B, F)

Where −

• Q may be a finite set of states

• X is that the tape alphabet

• ∑ is that the input alphabet

• δ may be a transition function; δ: alphabetic character × X → alphabetic character       × X ×

• q0 is that the initial state

• B is that the blank image

• F is that the set of ultimate states

Time and area quality of an information processing system

For an information processing system, the time quality refers to the live of variety|the amount|the quantity} of times the tape moves once the machine is initialized for a few input symbols and therefore the area quality is that the number of cells of the tape written.

Time quality all affordable functions −

T(n) = O(n log n)

TM’s area quality

S(n) = O(n)

5.1.2 Language Acceptability of Turing Machines

Even though they are recursively enumerable, the Turing machine embraces all the language. Recursive implies repeating for any number of times the same set of rules, and enumerable means a collection of elements.

Computable attributes, such as addition, multiplication, subtraction, division, power function, and many more are also accepted by the TM.

Example: Creating a turning machine which accepts the language of aba over ∑ = {a, b}

Sol: We'll think that the string 'aba' is positioned like this on the input tape:

The tape head reads the sequence up to the Δ characters. If the tape head is read 'aba' string, then after reading, TM will stop.

Now we're going to see how this turbo machine is going to work for aba. The condition is originally q0 and the head points to an as:

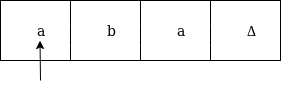
The next move are δ(q0, a) = δ(q1, A, R) which means it goes to state q1, replaced by A and  head moves toward  right :

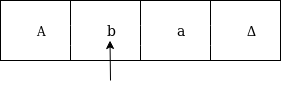
The next move are δ(q1, b) = δ(q2, B, R) which means it goes to state q2 , replaced by B and  head moves toward  right :

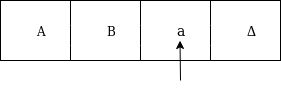
The next move are δ(q2, a) = δ(q3, A, R) which means it goes to state q3 , replaced by A and  head moves toward  right :

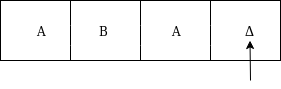
The move δ(q3, Δ) = (q4, Δ, S) therefore, it will go to state q4 which is the HALT state and HALT state is always an accept state for any Turing Machine .

The Turing machine can be represented by transition diagram -

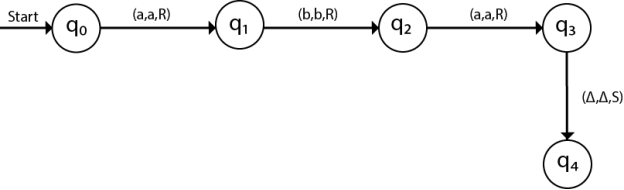
Fig. 1: transition diagram for Turing machine

5.1.3 Techniques for Turing Machine Construction

There are some techniques for Turing machine, which are -

●      Storage in finite control

Technique: - Using the finite control of a TM to hold a finite amount of data, in addition to the state.

Method: - Assuming the state as [q, A, B, C], for example, when the finite control holds three data elements A, B, and C.

Example:

Design a TM to recognize 01* + 10*. The set of states are of the form [qi, X] where qi = q1, q2; X = 0, 1, B.

• The control portion (state) remembers what the TM is doing (q0 = not read 1st symbol; q1 = reverse).

• The data portion remembers the first symbol seen (0, or 1).

The transition function d is as follows.

• d([q0, B], a) = ([q1, a], a, R) for a = 0, 1. --- Copying the symbol it scanned.

• d([q1, a],a) = ([q1, a],a, R) where ‘a is the complement of a = 0, 1. --- Skipping symbols which are complements of the 1st symbol read (stored in the state as a).

• d([q1, a], B) = ([q1, B], B, R) for a = 0, 1. --- Entering the accepting state [q, B] when reaching the 1st blank.

●      Multi tracks

➢      Assuming the tape of a TM as composed of several tracks.

➢      For example, if there are three tracks, we use the tape symbol as [X, Y, Z]

Example

The TM recognizes the non-CFL language

L = {wcw | w is in (0 + 1)+}.

Que: Why does not the power of the TM increase in this way?

Answer: just a kind of tape symbol labeling.

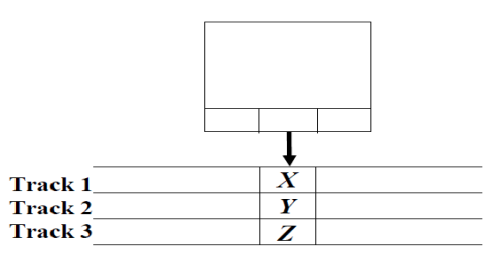
Fig 2: multi-track

●      Checking off symbols

We use one tape track to indicate that some symbols have Without modifying them, they are read.

Example: Consider a Turing machine for accepting

w#w#w, w ∈ {a, b}∗

Sol: A tape considered is two tracks.

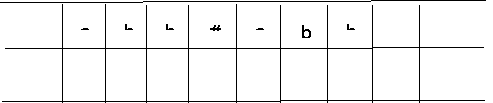
When the TM reads the first a in state q0, it stores it by taking the state as a pair) in its memory, checks off 'a by printing a 'in the second track below a, moves right and checks if the symbol is a' a 'after the # symbol.

If it is marked by putting a a √ in the second direction, it moves correctly and

The first symbol checks again after # is a 'a' and it also labels if so. For each unmarked, it then moves left and repeats the process in each block, the leftmost symbols.

The computer stops accepting the string if all the symbols in the first block match the second and third blocks.

The mapping as follow:

δ(q0, [a, 6b]) = ([q, a], [a, √], R)

δ(q0, [b, 6b]) = ([q, b], [b, √], R)

The TM starts reading from the leftmost symbol and marks it, also stored state and checks whether it is ‘a’ or ‘b’.

δ([q, a], [a, 6b]) = ([q, a], [a, 6b], R)

δ([q, a], [b, 6b]) = ([q, a], [b, 6b], R)

δ([q, b], [a, 6b]) = ([q, b], [a, 6b], R)

δ([q, b], [b, 6b]) = ([q, b], [b, 6b], R)

In the first block to the right, the head moves through symbols

δ([q, a], [#, 6b]) = ([p, a], [#, 6b], R)

δ([q, b], [#, 6b]) = ([p, b], [#, b], R)

In the first track, when the head encounters a #, the first state component is changed to p

δ([p, a], [a, √]) = ([p, a], [a, √], R)

δ([p, a], [b, √]) = ([p, a], [b, √], R)

δ([p, b], [a, √]) = ([p, b], [a, √], R)

δ([p, b], [b, √]) = ([p, b], [b, √], R)

δ([p, a], [a, 6b]) = ([r, a], [a, √], R)

δ([p, b], [b, 6b]) = ([r, b], [b, √], R)

When a first unchecked symbol is found, it marks it by placing a √ in the second direction and changing the first component of the state to r.

δ([r, a], [a, 6b]) = ([r, a], [a, 6b], R)

δ([r, b], [a, 6b]) = ([r, b], [a, 6b], R)

δ([r, a], [b, 6b]) = ([r, a], [b, 6b], R)

δ([r, b], [b, 6b]) = ([r, b], [b, 6b], R)

When the first part of the state is r, the head moves through the second block without changing symbols

δ([r, a], [#, 6b]) = ([s, a], [#, 6b], R)

δ([r, b], [#, 6b]) = ([s, b], [#, 6b], R)

It moves straight into the third block when it encounters a # in the first track, changing the first component of the state to s

δ([s, a], [a, √]) = ([s, a], [a, √], R)

δ([s, a], [b, √]) = ([s, a], [b, √], R)

δ([s, b], [a, √]) = ([s, b], [a, √], R)

δ([s, b], [b, √]) = ([s, b], [b, √], R)

This goes right in search of the unchecked symbol

δ([s, b], [b, 6b]) = (t, [b, √],L)

δ([s, a], [a, 6b]) = (t, [a, √],L)

If an unchecked sign is found in the third, it marks it by placing a √  in the second direction and begins heading left.

δ(t, [a, √]) = (t, [a, √],L)

δ(t, [b, √]) = (t, [b, √],L)

δ(t, [#, √]) = (t0, [#, √],L)

In state t ', it passes into the second block

δ(t0, [a, 6b]) = (t0, [a, 6b],L)

δ(t0, [b, 6b]) = (t0, [b, 6b],L)

δ(t0, [a, √]) = (t0, [a, √],L)

δ(t0, [b, √]) = (t0, [b, √],L)

In second block, it moves left

δ(t0, [#, 6b]) = (t00, [#, b],L)

In the first block , moves left in state t”

δ(t00, [a, 6b]) = (t00, [a, 6b],L)

δ(t00, [b, 6b]) = (t00, [b, 6b],L)

In the first block it moves left through an unchecked symbol.

When it faces a checked symbol, it moves right in the state q0 and repeat the whole process.

δ(t00, [a, √]) = (q0, [a, √], R)

δ(t00, [b, √]) = (q0, [b, √], R)

In this manner, the computer scans for the same symbols in the

Lines, first, second and third

●      Subroutine

Much as a computer program has a primary procedure and procedure the TM can also be programmed to have subroutines, A core TM and TMs that function as subroutines.

Suppose we're going to make n copies of a word w Input is #w# and the output is #w# w| ww{z. . . w} n times.

In this situation, we can compose the mappings for a TM Msub That ends with #w#xw when launched on #w#x. This is called Msub x times by the key TM.

Likewise, for Multiplying two unary numbers m and n, on m occasions, n must be copied. For copying we can write a sub TM and main TM will name this m times.

The M1 and M2 states must be disjointed in order for a Turing machine M1 to use another Turing machine M2 as a subroutine. The control also goes to the initial state of M2 when M1 wishes to call M2, from the state of M1. When the subroutine stops and returns to M1, from M2's stopping state, the subroutine returns to M2 the computer goes into a certain M1 mode.

Note that a subroutine Turing Machine calls its subroutine another turing machine (TM). To construct a Turing machine in a top-down way, separating the job into tasks and writing .

5.1.4 Modifications of Turing Machine

A typical Turing Machine is a machine that moves either to the left or right when an input is given and it can overwrite the current symbol.

A Turing Machine can be described as a 7-tuple:

(Q, X, *, f, q0, B, F)

Where,

Q - finite set of state

X - tape alphabet

* - input alphabet

f - transition function

f: Q x X - - > Q x X x { left_shift , right_shift }

q0 - initial state

B - blank symbol

F - set of final state

Some languages, called recursively enumerable languages, can be accepted by a regular Turing machine.

Let's see if we can increase the number of languages recognized by the Turing Machine by doing some form of modification.

1. Turing machine with stay option

If the head could still remain in one position without moving anywhere instead of moving left or right on seeing an input, i.e.

f: Q x X - - > Q x X x {left_shift , right_shift}

The number of languages recognized by the Turing machine is still the same.

We know that a Turing machine has an infinite input tape with extends in both the direction (left or right). So now if we restrict it to extend only in one direction and not in both the directions, i.e. We make the tape semi-infinite, so the number of languages the Turing machine accepts remains the same as well.

Both the input and output are present on the tape in the traditional turing machine , the head has the power to travel over the input and can alter or change the input , if we don’t want to change the input we can have the input in a separate file, which is ready only then the head can’t make changes to it.

If the Turing machine needs to alter the input, it is important to copy the input to the tape and the header will make the changes, but the input file stays unchanged as changes are made to the tape and not to the file. By making such improvements to the Turing machine, the number of languages recognised by the Turing machine remains the same.

The head of the regular Turing machine can move only one step to the right or left, but the head can move not only one step to the left or right if the Turing machine leaps, but it can move more than one step, i.e. 2, 3, 4, 5, 6,... Etc., or it can jump to any cell on the right or left of the input tape.

f: Q x X - - > Q x X x {left_shift, right_shift} x {n}

N is the number of moves we want to pass to the left or right. But the languages accepted by the Turing machine are still similar.

The input symbol can be converted to blank in the regular Turing machine, but if we eliminate this facility to change the input symbol to blank, this type of Turing machine is called a non-erasing Turing machine. We may substitute any other symbol other than blank for the input. The number of languages recognized by the Turing machine remains the same despite this update.

Standard Turing machine gives us the power to leave it as it is without making any adjustments when seeing an input, but it is necessary to modify the input once we see it. We cannot leave it as it is in always writing Turing machine. But this kind of change did not help to increase the number of languages that the Turing machine approved.

Therefore, after making so many changes to the Turing machine, we see that the number of languages recognized by it is still the same. The Turing Machine is thus the most efficient machine.

5.1.5 Turing Machine as Computer of Integer Functions

Simulating a TM by Computer -

➢      A real computer is actually a finite automaton!

➢      Simulation of an infinite memory space by “storage swapping.”

➢      Also, simulation of an infinite tape of the TM by two stacks of disks, respectively for the left portion and the right portion of the tape, with the head as the middle.

Simulating a Computer by a TM -

Sketch of using a Multitape TM to simulate the sequence of instructions of the computer and use a TM tape:

• as the computer memory;

• to simulate the instruction counter;

• for the memory address;

• as scratch to perform computation operations on it.

5.1.6 Universal Turing machine

The mathematical device similar to a digital computer is the Turing Machine. It was proposed in the 1930s by the mathematician Turing, and has been the most commonly used computer model in the theory of computability and complexity since then.

The model consists of an input relationship between the output that the computer calculates. On the machine's tape, the input is supplied in binary form, and the output consists of the tape content when the machine stops.

Within the Turing Machine, what decides how the contents of the tape shift is a finite state machine (or FSM, also called a finite automaton). The FSM has been the number of states it has and the transitions between them are determined by the number.

The current state and the character read on the tape decide at each step the next state that the FSM will be in the character that the computer will generate on the tape (possibly the one that reads, leaving the contents unchanged), and the direction in which the head travels, left or right.

The problem with Turing Machines is that for each new computation to be performed, for each input output reference, a separate one must be constructed.

This is why we are implementing the idea of a Universal Turing Machine (UTM), which   the definition of a system M is used along with the input on the tape. The UTM will then simulate M on the rest of the content of the input tape to simulate.

A universal turing machine can thus simulate any other machine.

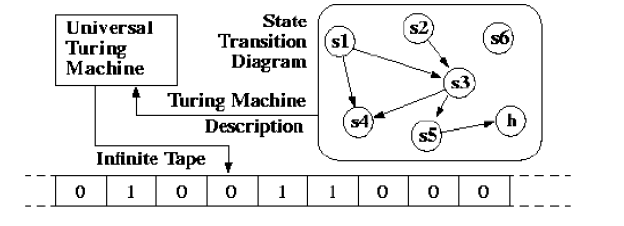
Fig 3: Universal Turing machine

Key takeaways:

-         A mathematical model consisting of an associated infinite length tape divided into cells on which input is given may be an information processing device (TM)

-         Computable attributes, such as addition, multiplication, subtraction, division, power function, and many more are also accepted by the TM.

-         A real computer is actually a finite automaton.

5.2 Linear Bounded Automata

A multi-track non-deterministic Turing machine with a tape of some limited finite length is a linear bounded automaton.

Length = function (Length of the initial input string, constant c)

Here,

Memory information ≤ c × Input information

The measurement is limited to the region bounded by constants. There are two special symbols in the input alphabet that act as left end markers and right end markers, indicating that the transitions do not switch either to the left of the left end marker or to the right of the tape's right end marker.

A linear bounded automaton can be defined in 8-tuple -

(Q, X, ∑, q0, ML, MR, δ, F)

Where

●       Q is a finite set of states

●       X is the tape alphabet

●       ∑ is the input alphabet

●       q0 is the initial state

●       ML is the left end marker

●       MR is the right end marker where MR ≠ ML

●       δ is a transition function which maps each pair (state) to (state, tape symbol, Constant ‘c’) where c could become 0 or +1 or -1.

●       F is the set of final states.

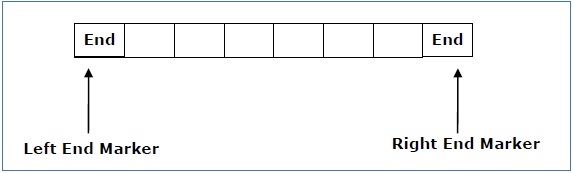
Fig 4: linear bounded automata

Note -

-         The measurement is limited to the region bounded by constants.

-         A linear bounded automaton is a multi-track non-deterministic Turing machine with a tape of some limited finite length.

5.3 Church’s Thesis

In 1936, a technique named as lambda-calculus was created by Alonzo Church within which the Church numerals area unit well outlined, i.e. the encryption of natural numbers. Additionally in 1936, mathematician machines (earlier known as theoretical model for machines) was created by mathematician, that’s used for manipulating the symbols of string with the assistance of tape.

Church mathematician Thesis:

Turing machine is outlined as associate degree abstract illustration of a computer like hardware in computers. Mathematician planned Logical Computing Machines (LCMs), i.e. mathematician’s expressions for Turing Machines. This was done to outline algorithms properly. So, Church created a mechanical methodology named

As ‘M’ for manipulation of strings by mistreatment logic and arithmetic.

This methodology M should pass the subsequent statements:

• Number of directions in M should be finite.

• Output ought to be made when playing a finite variety of steps.

• It mustn’t be imagined, i.e. is created in the world.

• It mustn’t need any complicated understanding.

Using these statements Church planned a hypothesis known as Church’s mathematician thesis that may be expressed as: “The assumption that the intuitive the notion of estimable functions is known with partial algorithmic functions.”

In 1930, this statement was initial developed by Alonzo Church and is typically brought up as Church’s thesis, or the Church-Turing thesis. However, this hypothesis cannot be proved.

The algorithmic functions are estimable when taking following assumptions:

1. Every and each operate should be estimable.
2. Let ‘F’ be the estimable operate and when playing some elementary operations to ‘F’, it’ll rework a replacement operate ‘G’ then this operate ‘G’ mechanically becomes the estimable operate.
3. If any operates that follow on top of 2 assumptions should be states as an estimable function.

Note -

For manipulation of strings by mistreatment logic and arithmetic, Church developed a mechanical technique called 'M'.

5.4 Recursive and Recursively Enumerable language

Recursive language (RE) –

A language ‘L’ is alleged to be algorithmic if there exists a computing device which is able to settle for all the strings in ‘L’ and reject all the strings not in ‘L’. The computing device can halt on every occasion and provides associate answer (accepted or rejected) for every and each string input. A language ‘L’ is decidable if it’s a algorithmic language. All decidable languages area unit algorithmic languages and vice-versa.

Recursively countable language (RCE) –

A language ‘L’ is alleged to be a recursively countable language if there exists a computing device which is able to settle for (and so halt) for all the input strings that area unit in ‘L’ however could or might not halt for all input strings that aren’t in ‘L’.

By definition, all REC languages {are also|also area unit|are} RE languages however not all RE languages are REC languages.

A language is termed Decidable or algorithmic if there’s a data processor that accepts and halts on each input string w. Each decidable language is Turing-Acceptable.

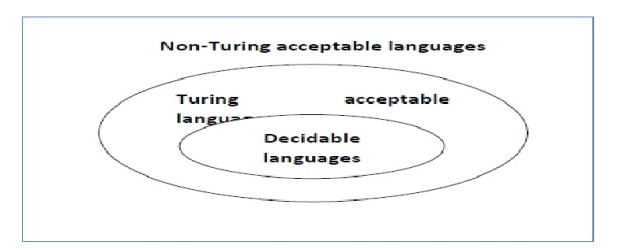
Fig 5

A decision downside P is decidable if the language L of all affirmative instances to P

Is decidable.

For a decidable language, for every input string, the thulium halts either at the settle

For or the reject state as pictured within the following diagram –

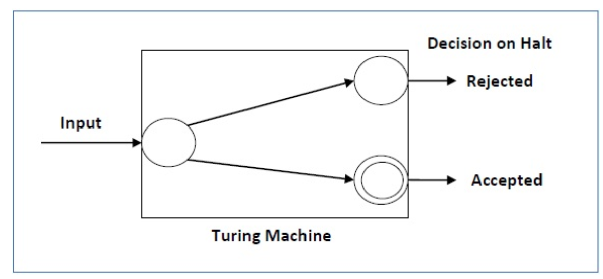
Fig 6

5.5 Halting Problem

Input: A Turing machine and an input string T.

Problem - Does the Turing machine complete the T-string computation in a finite number of steps? Either yes or no must be the answer.

Sol:  We will first assume that there is such a Turing machine to solve this problem, and then we will demonstrate that it contradicts itself. This Turing machine would be called a Halting machine that produces in a finite amount of time a 'yes' or no'. The performance comes as 'yes' if the stopping machine finishes in a finite amount of time, otherwise as no'.

The following is a Halting Computer block diagram -

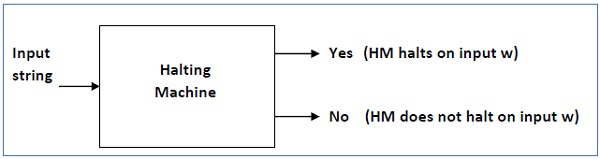
Fig 7: halting machine

Now we will design an inverted halting machine (HM)’ as -

●       If H returns YES, then loop forever.

●       If H returns NO, then halt.

Below is the block diagram of inverted halting machine -

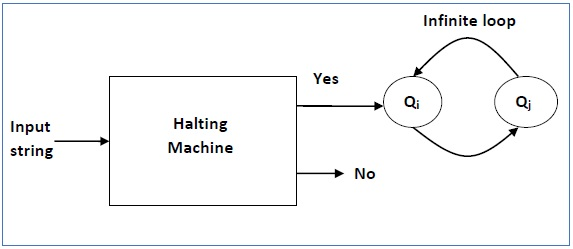
Fig 8: inverted halting machine

In addition, as follows, a machine (HM)2 whose input itself is constructed -

●       If - (HM)2 halts on input, loop forever

●       Else - halt

Now, we have a contradiction. So, the halting problem is undecidable.

5.6 Post’s Correspondence Problem

It was introduced by Emil Post and is an undecidable decision problem. The PCP problem over an alphabet ∑ is stated as follows −

Given the following two lists, M and N of non-empty strings over ∑ −

M = (x 1, x 2, x 3 ,………, x n )

N = (y 1, y 2, y 3 ,………, y n )

We can say that there is a Post Correspondence Solution, if for some i 1, i 2……… i k,

Where 1 ≤ i j ≤ n, the condition x i1 …….x ik = y i1 ……. y ik satisfies.

Example 1

Find whether the lists

M = (abb, aa, aaa) and N = (bba, aaa, aa)

Have a Post Correspondence Solution?

Sol:

Here,

x2 x1 x3  = ‘aaabbaaa’

And y2 y1 y3  = ‘aaabbaaa’

We can see that

x2 x1 x3  = y2 y1 y3

Hence, the solution is i = 2, j = 1, and k = 3.

Example 2

Find whether the lists M = (ab, bab, bbaaa) and N = (a, ba, bab) have a Post

Correspondence Solution?

Sol:

In this case, there is no solution because −

| x 2 x 1 x 3 | ≠ | y 2 y 1 y 3 | (Lengths are not same)

Hence, it can be said that this Post Correspondence Problem is undecidable.

5.7 Introduction to Recursive Function Theory

Total recursive function -

If f(a1, a2, ...an) is defined for all its arguments, a recursive function is called the complete recursive function. Let f(a1, a2, ...an) be a function defined for function g(b1, b2, ...bn). If each element of f is assigned to a unique element of function g, then f is a total function.

●      A complete function is called recursive or primitive recursive if and only if it is an initial over-n function, or if it is obtained by applying a finite number of times composition or recursion to an initial over-n function.

●      A complete recursive function or primitive recursive function is the multiplication of two positive integers.

●      Not all complete recursive functions are recursive primitive functions.

●      The function of Ackerman is a complete function.

●      Both primitive recursive features are complete functions.

Partial recursive function -

A function f(a1, a2,....an) determined by a TM is referred to as a partial recursive function. If f is defined for some but not all values of a1, a2,....an. Let f(a1, a2,...an) be a function defined by function g(b1, b2,....bn), then f is a partial function if almost one element of function g is assigned to some element of f.

If it is an initial function over N, a partial function is recursive, or if it is obtained by applying recursion or composition or minimization to an initial function over N.

●      The partial recursive function is the subtraction of two positive integers.

●      The partial function composition yields a partial(total) function.

●      A partial recursive function is the minimization of a complete recursive function.

References:

1. Theory of Computer Science (Automata, Languages and Computation), 2e by

K. L. P. Mishra and N. Chandrasekharan, PHI

2. Introduction to Automata Theory, Languages, and Computation, 2e by John E,

Hopcroft, Rajeev Motwani, Jeffery D. Ullman, Pearson Education.