Unit – 1
Introduction to Compiler
● A compiler is a translator that translates the language at the highest level into the language of the computer.
● A developer writes high-level language and the processor can understand machine language.
● The compiler is used to display a programmer's errors.
● The main objective of the compiler is to modify the code written in one language without altering the program's meaning.
● When you run a programme that is written in the language of HLL programming, it runs in two parts.
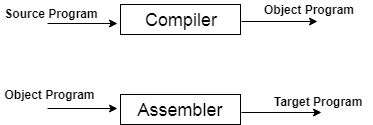
Fig 1: Execution process of Compiler
Phases and passes
Phases -
The method of compilation includes the sequence of different stages. Each phase takes a source programme in one representation and produces output in another representation. From its previous stage, each process takes input.
The various stages of the compiler take place:
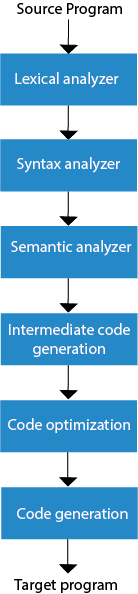
Fig 2: phases of compiler
Passes -
Pass is a full source software traversal. The programmer has two passes through the source programme to traverse it.
Multi-pass compiler -
One - pass compiler -
Key takeaway:
- Each phase takes a source programme in one representation and produces output in another representation.
- The method of compilation includes the sequence of different stages.
- Pass is a full source software traversal.
- The programmer has two passes through the source programme to traverse it.
Bootstrapping is commonly used in the production of compilations.
In order to generate a self-hosting compiler, bootstrapping is used. Self-hosting is a type of compiler that is capable of compiling its own source code.
To compile the compiler, the Bootstrap compiler is used, and then you can use this compiled compiler to compile all else and future versions of the compiler itself.
Three languages can characterize a compiler:
A SCIT compiler for source S, Goal T, implemented in I, is shown in the T- diagram.
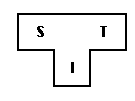
To generate a new language L for machine A, follow some steps:
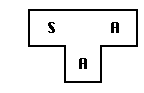
2. Build an LCSA compiler for language L that is written in a subset of L.
3. Compile LCSA using the compiler SCAA to obtain LCAA. LCAA is a compiler for language L, which runs on machine A and produces code for machine A.

Bootstrapping is called the mechanism defined by the T-diagrams.
Key takeaway:
- Bootstrapping is commonly used in the production of compilations
- To generate a self-hosting compiler, bootstrapping is used.
➢ To identify patterns, finite state machines are used.
➢ The Finite Automated System takes the symbol string as input and modifies its state accordingly. When the desired symbol is found in the input, then the transformation happens.
➢ The automated devices may either switch to the next state during the transition or remain in the same state.
➢ FA has two states: state approve or state deny. When the input string is processed successfully and the automatic has reached its final state, it will approve it.
The following refers to a finite automatic:
Q: a finite set of states
∑: a finite set of the input symbol
q0: initial state
F: final state
δ: Transition function
It is possible to describe transition functions as
δ: Q x ∑ →Q
The FA is described in two ways:
DFA
DFA stands for Deterministic Finite Automata. Deterministic refers to computational uniqueness. In DFA, the character of the input goes to only one state. The DFA does not allow the null shift, which means that without an input character, the DFA does not change the state.
DFA has five tuples {Q, ∑, q0, F, δ}
Q: a set of all states
∑: a finite set of input symbol where δ: Q x ∑ →Q
q0: initial state
F: final state
δ: Transition function
NDFA
NDFA applies to Finite Non-Deterministic Automata. It is used for a single input to pass through any number of states. NDFA embraces the NULL step, indicating that without reading the symbols, it can change the state.
Like the DFA, NDFA also has five states. NDFA, however, has distinct transformation features.
NDFA's transition role may be described as:
δ: Q x ∑ →2Q
Key takeaway:
- To identify patterns, finite state machines are used.
- FA has two states: state approve or state deny.
- In DFA, the character of the input goes to only one state.
- It is used for a single input to pass through any number of states.
The lexical analyzer requires only a finite set of valid string/token/lexeme that belongs to the language in hand to be scanned and defined. It looks for the pattern that the language rules describe.
By defining a pattern for finite strings of symbols, regular expressions can express finite languages. Regular grammar is referred to as the grammar described by regular expressions. The standard language is regarded as the language described by the regular grammar.
For defining patterns, a regular expression is a significant notation. Each pattern matches a string set, so regular expressions function as string set names. Regular languages can be represented by programming language tokens. An instance of a recursive description is the specification of regular expressions. Regular languages are easy to understand and execute effectively.
There are a variety of algebraic rules that can be used to manipulate regular expressions into analogous forms that are obeyed by regular expressions.
Precedence and Associativity
● The associative *, concatenation (.), and | (pipe sign) are left.
● * Has the highest priority
● Concatenation (.) has the highest second precedence.
● | (pipe sign) has the lowest of all precedents.
Representing in standard expression authentic tokens of a language
If x is a normal expression, then:
➔ x* implies the occurrence of x at zero or more.
It is capable of generating {e, x, xx, xxx, xxxx, xxxx,... }
➔ x+ implies one or more instances of x.
In other words, { x, xx, xxx, xxx, xxxx... } or x.x* can be generated.
➔ x? Means one instance of x at most
It can, for example, generate either {x} or {e}.
All the lower-case English language alphabets are [a-z].
Both English language upper-case alphabets are [A-Z].
All the natural digits used in mathematics are [0-9].
Representing tokens of language using regular expressions
Decimal = (sign)?(digit)+
Identifier = (letter)(letter | digit)*
How to check the validity of a regular expression used in defining the patterns of keywords in a language is the only issue left with the lexical analyzer. The use of finite automata for verification is a well-accepted approach.
Key takeaway:
- By defining a pattern for finite strings of symbols, regular expressions can express finite languages.
- Regular grammar is referred to as the grammar described by regular expressions.
We identify three algorithms that have been used to implement pattern matchers designed from regular expressions and optimize them.
In a Lex compiler, the first algorithm is useful because it creates a DFA directly from a regular expression without constructing an NFA intermediate. The resulting DFA can also be constructed through an NFA with fewer states than the DFA.
The second algorithm minimizes the number of states of any DFA, by combining states that have the same future behaviour. The algorithm itself is very efficient, running at time 0(n log n), where n is the DFA's number of states.
The third algorithm produces transformation tables with more compact representations than the regular, two-dimensional table.
Lex is a lexical analyzer generating programme. It is used to produce the YACC parser. Software that transforms an input stream into a sequence of tokens is the lexical analyzer. It reads the input stream and, by implementing the lexical analyzer in the C programme, produces the source code as output.
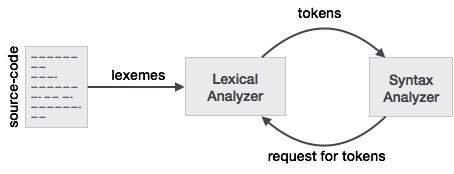
Fig 3: lexical analyzer generator
If a token is considered invalid by the lexical analyzer, it produces an error. The lexical analyzer works with the syntax analyzer in close collaboration. It reads character streams from the source code, checks for legal tokens, and, when necessary, passes the information to the syntax analyzer.
Tokens
It is said that lexemes are a character sequence (alphanumeric) in a token. For each lexeme to be identified as a valid token, there are some predefined rules. These rules, by means of a pattern, are described by grammar rules. A pattern describes what a token can be, and by means of regular expressions, these patterns are described.
Keywords, constants, identifiers, sequences, numbers, operators, and punctuation symbols can be used as tokens in the programming language.
Example: the variable declaration line in the C language
int value = 100 ;
contains the tokens:
int (keyword) , value (identifiers) = (operator) , 100 (constant) and ; (symbol)
Key takeaway:
- It is said that lexemes are a character sequence (alphanumeric) in a token.
- For each lexeme to be identified as a valid token, there are some predefined rules.
- Lexical analyzer is used to produce the YACC parser
Functions of lex:
● Firstly, in the language of Lex, the lexical analyzer produces a lex.1 programme. The Lex compiler then runs the lex.1 programme and generates the lex. yy.c C programme.
● Finally, the programmer C runs the programme lex.yy.c and generates the object programme a.out.
● A.out is a lexical analyzer that converts an input stream into a token sequence.
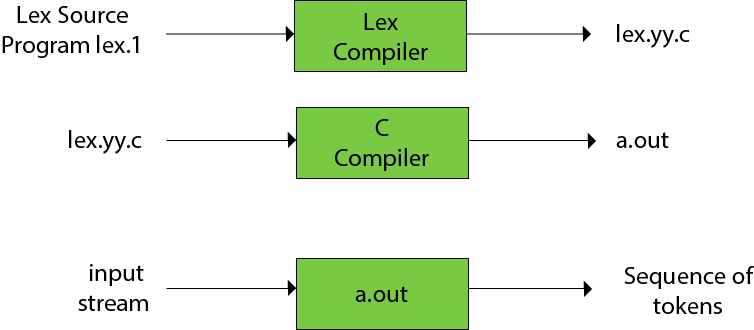
Fig 4: Lex compiler
Lex file format:
By percent delimiters, a Lex programme is divided into three parts. The structured sources for Lex are as follows:
{ definitions }
%%
{ rules }
%%
{ user subroutines }
Definitions include constant, variable, and standard meaning declarations.
The rules describe the form statement p1 {action1} p2 {action2}....pn {action} p2 form p1....pn {action}
Where pi describes the regular expression and action1 describes the behaviour that should be taken by the lexical analyzer when a lexeme matches the pattern pi.
Auxiliary procedures required by the acts are user subroutines. It is possible to load the subroutine with the lexical analyzer and compile it separately.
Key takeaway:
- In the language of Lex, the lexical analyzer produces a lex.1 programme.
- The Lex compiler then runs the lex.
A set of rules is formal grammar. It is used in a language to distinguish right or wrong strings of tokens. The formal grammar is shown as G.
Formal grammar is used to generate all possible strings that are syntactically correct in the language using the alphabet.
Formal grammar is often used during the compilation process of syntactic analysis (parsing).
As folows, formal grammar G is written:
G = <V, N, P, S>
Where:
N - a finite set of non-terminal symbols.
V - a finite set of terminal symbols.
P - set of production rules
S - start symbol.
Example:
L = {a, b}, N = {S, R, B}
Production rules:
We may generate some strings through this production, such as bab, baab, baaab, etc.
This output describes the banab - shape string.
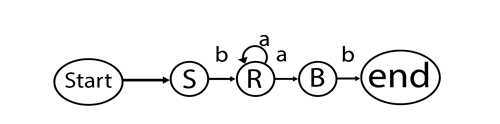
Fig 5: Formal language
Key takeaway:
- Formal grammar is used to generate all possible strings that are syntactically correct in the language using the alphabet.
- A set of rules is formal grammar.
BNF stands for Backus-Naur Form. It is used to write a formal representation of grammar that is context-free. It is often used to define a programming language's syntax.
Basically, BNF notation is just a version of context-free grammar.
Productions at the BNF take the form of:
Left side → definition
If left side∈ (Vn∪ Vt)+ and (definition) concept ∈ (Vn∪ Vt)*. In BNF, one non-terminal is found on the left line.
The various productions with the same left side can be identified. The vertical bar symbol "|" is used to distinguish all productions.
For any grammar, the output is as follows:
In BNF, the grammar above can be expressed as follows:
S → aSa| bSb| c
Key takeaway:
- It is used to write a formal representation of grammar that is context-free.
- It is often used to define a programming language's syntax.
If there is more than one leftmost derivation or more than one rightmost derivative or more than one parse tree for the given input string, grammar is said to be ambiguous. It's called unambiguous if the grammar is not vague.
Example:
The above grammar produces two parse trees for the string Aabb:
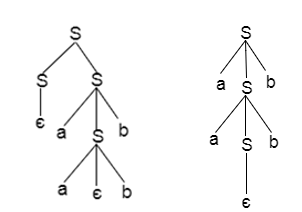
If there is uncertainty in the grammar, then it is good for constructing a compiler.
No method can detect and remove ambiguity automatically, but by re-writing the entire grammar without ambiguity, you can remove ambiguity.
Key takeaway:
- If there is more than one left or rightmost derivation or more than one parse tree for the given input string, grammar is said to be ambiguous.
● YACC stands for Compiler Compiler Yet Another.
● For a given grammar, YACC provides a method to generate a parser.
● YACC is a software designed to compile the grammar of LALR(1).
● It is used to generate the source code of the language syntactic analyzer provided by LALR (1) grammar.
● The YACC input is a rule of grammar, and a C programme is the output.
Some points about YACC are as follows:
Input: A CFG- file.y
Output: A parser y.tab.c (yacc)
● The output file "file.output" includes tables of parsing.
● There are declarations in the file 'file.tab.h'.
● Yyparse was named by the parser ().
● To get tokens, Parser expects to use a function called yylex ().
The following is the essential operational sequence:
In YACC format, this file contains the desired grammar.
YACC software is seen.
It is the YACC-generated c source software.
C - compiler
Executable file to decode grammar defined in gram. YY.
Key takeaway:
- The YACC input is a rule of grammar, and a C programme is the output.
- For a given grammar, YACC provides a method to generate a parser.
A context-free grammar is a formal grammar that is used in a given formal language to generate all possible strings.
Four tuples can be described by Context-free grammar G as:
G= (V, T, P, S)
Where,
G - grammar
T - a finite set of terminal symbols.
V - a finite set of non-terminal symbols
P - set of production rules
S - start symbol.
In CFG, to derive the string, the start symbol is used. You may extract a string by replacing a non-terminal on the right side of the output repeatedly until all non-terminals are replaced with terminal symbols.
Example:
L= {wcwR | w € (a, b)*}
Production rule:
Now, verify that you can derive the abbcbba string from the given CFG.
By recursively applying the production S → aSa, S → bSb, and finally applying the production S → c, we get the abbcbba series.
Key takeaway:
- In CFG, to derive the string, the start symbol is used.
- A context-free grammar is a formal grammar that is used in a given formal language to generate all possible strings.
The derivation is a sequence of the laws of development. Via these production laws, it is used to get the input string. We have to make two decisions during parsing. Those are like the following:
● The non-terminal that is to be replaced must be determined by us.
● We have to determine the law of development by which the non-terminal would be substituted.
We have two choices to determine which non-terminal is to be replaced by the rule of output.
Leftmost derivation:
The input is scanned and replaced with the development rule from left to right in the left-most derivation. In most derivatives on the left, the input string is read from left to right.
Example:
Production rules:
Input
a - b + c
The left-most derivation is:
S = S + S
S = S - S + S
S = a - S + S
S = a - b + S
S = a - b + c
Right most derivation:
The input is scanned and replaced with the development rule from right to left in the rightmost derivation. So, we read the input string from right to left in most derivatives on the right.
Example:
Input:
a - b + c
The right-most derivation is:
S = S - S
S = S - S + S
S = S - S + c
S = S - b + c
S = a - b + c
Parse Tree
● The graphical representation of symbols is the Parse tree. Terminal or non-terminal may be the symbol.
● In parsing, using the start symbol, the string is derived. The starter symbol is the root of the parse tree.
● It is the symbol's graphical representation, which can be terminals or non-terminals.
● The parse tree follows the operators' precedence. The deepest sub-tree went through first. So, the operator has less precedence over the operator in the sub-tree in the parent node.
Following these points, the parse tree:
● The terminals have to be all leaf nodes.
● Non-terminals have to be all interior nodes.
● In-order traversal supplies the initial string of inputs.
Example
Production rules:
Input
a * b + c
Step 1:
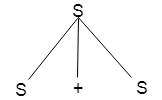
Step 2:
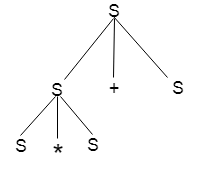
Step 3:
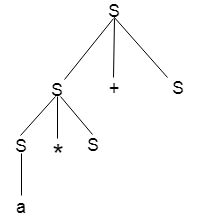
Step 4:
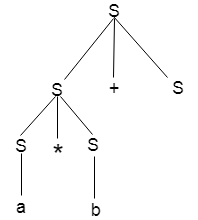
Step 5:
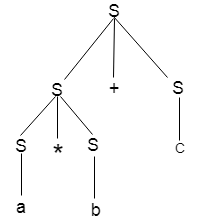
Key takeaway:
- The derivation is a sequence of the laws of development.
- We have to make two decisions during parsing.
- In most derivatives on the left, the input string is read from left to right.
- The parse tree follows the operators' precedence.
The various capabilities of CFG exist:
References: