Unit - 3

Syntax-directed Translation

3.1 Syntax-directed Translation schemes

In syntax-directed translation, certain informal notations are associated with the grammar and these notations are called semantic rules.

Therefore, we may say that

Grammar + semantic rule = SDT (syntax directed translation) 

●      In syntax-directed translation, depending on the form of the attribute, each non-terminal may get one or more attributes, or sometimes 0 attributes.

●      Semantic rules aligned with the output rule determine the value of these attributes.

●      Whenever a construct meets in the programming language in Syntax driven translation, it is translated according to the semantic rules specified in that particular programming language.

Example :

One of E's attributes is E.val.

The attribute returned by the lexical analyzer is num.lexval.

Key takeaway :

-         By adding attributes to grammatical symbols, we may associate knowledge with a language construct.

-         The syntax-directed description defines attribute values by associating the semantic rules with the grammatical outputs.

3.2 Implementation of Syntax-directed Translators

By building a parse tree and performing the act's first order in a left to the right depth, syntax-directed translation is implemented.

Syntax Directed Translation is an improved grammar law that makes semantic analysis easier. In the form of attributes attached to the nodes, SDT requires moving data bottom-up and/or top-down to the parse tree.

Syntax Directed translation rules use, in their meanings,

1) lexical values of nodes,

2) constants &

3) attributes associated with non-terminals.

The general approach to Syntax-Directed Translation is to create a parse tree or syntax tree and, by visiting them in some order, compute the attribute values at the nodes of the tree. In certain instances, without creating an explicit tree, translation can be achieved during parsing.

Example

Parse tree for SDT :

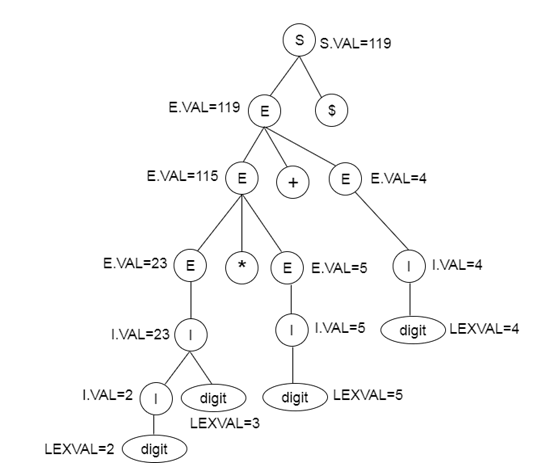
Fig 1: parse tree for SDT

Key takeaway :

-         SDT is implemented by parsing the input and, as a result, creating a parse tree.

-         Syntax Directed Translation is an improved grammar law that makes semantic analysis easier.

3.3 Intermediate code

To convert the source code into the computer code, intermediate code is used. Between the high-level language and the computer language lies the intermediate code.

Fig 2: the position of the intermediate code generator

❏      If the compiler converts the source code directly into the machine code without creating intermediate code, then each new machine needs a complete native compiler.

❏      For all compilers, the intermediate code holds the research section the same, which is why it does not require a complete compiler for each specific machine.

❏      Input from its predecessor stage and semantic analyzer stage is obtained by the intermediate code generator. This takes feedback in the form of an annotated tree of syntax.

❏      The second stage of the compiler synthesis process is modified according to the target machine by using the intermediate code.

Intermediate representation :

It is possible to represent the intermediate code in two ways:

The intermediate code of the high level can be interpreted as the source code. We can easily add code modifications to boost the performance of the source code. Yet there is less preference for optimizing the goal machine.

2.     Low-level intermediate code :

The low-level intermediate code is similar to the target computer, making it ideal for registering and allocating memory, etc. It is used for optimizations depending on the machine.

Key takeaway :

-         It lies between the high-level language and computer language.

-         The intermediate code of the high level can be interpreted as the source code.

-         It is used for optimizations depending on the machine.

3.4 Postfix notation

●      If the language given is expressions, the Postfix notation is a useful type of intermediate code.

●      Postfix notation is sometimes referred to as 'reverse polish' and 'suffix notation'.

●      A linear representation of a syntax tree is the Postfix notation.

●      Any expression can be written unambiguously without parentheses in the postfix notation.

●      The ordinary way (infix) to write the number of a and b is with the middle operator: a * b. In the postfix notation, however, we position the operator as ab * at the right end.

●      The operator obeys the operand in postfix notation.

Example :

Production

Example :

a := b * -c + b * -c

Postfix notation of given above  statement :

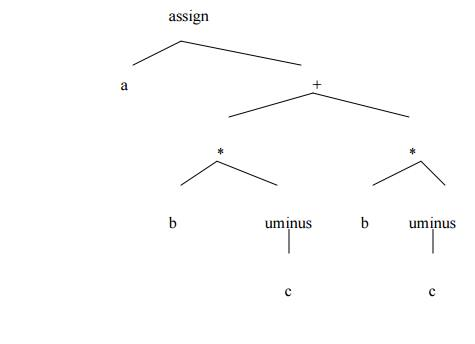
Fig 3: postfix notation

Key takeaway :

-         A linear representation of a syntax tree is the Postfix notation.

-         It is a list of tree nodes where a node occurs immediately after children.

3.5 Parse trees & syntax trees

Parse Tree

It contains more information than needed when you build a parse tree. It's very hard, therefore, to decode the parse tree compiler.

According to some context-free grammar, the parse tree reflects the syntactic structure of a string. It defines the input language's syntax. For various types of constituents, the parse tree does not use separate symbol forms.

Phrase structure grammars or dependency grammars are the basis for constructing a parse tree. Parse trees can be created for natural language phrases and when processing programming languages.

Take the following tree as an example :

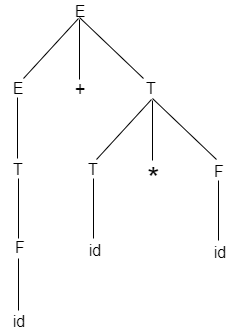
Fig 4: parse tree

●      The bulk of the leaf nodes in the parse tree are single-child to their parent nodes.

●      We may delete this extra information in the syntax tree.

●      A version of the parse tree is a syntax tree. Interior nodes are operators in the syntax tree and leaves are operands.

●      The syntax tree is typically used when the tree structure describes a programme.

Syntax Tree

The abstract syntactic structure of source code written in a programming language is represented by a syntax tree. Rather than elements such as braces, semicolons that end sentences in some languages, it focuses on the laws.

It is also a hierarchy divided into many parts with the elements of programming statements. The tree nodes denote a construct that exists in the source code.

A form id + id * id will have the following tree of syntax:

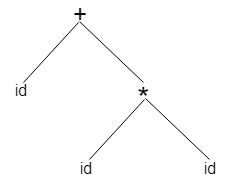
It is possible to represent the Abstract Syntax Tree as:

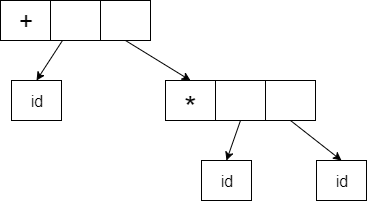
Fig 5: syntax tree

In a compiler, abstract syntax trees are significant data structures. It includes the least information that is redundant.

Key takeaway :

-         Abstract syntax trees are more compact and can easily be used by a compiler than a parse tree.

-         The syntax tree helps evaluate the compiler's accuracy.

-         A parse forest is a collection of possible parse trees for a syntactically ambiguous word.

3.6 Three address code

An intermediate code is a three-address code. It is used by the compilers that optimize it. The provided expression is broken down into multiple separate instructions in the three-address code. Such instructions can be easily translated into the language of assembly.

Any instruction for the three address code has three operands at most. It is a combination of a binary operator and a mission

The compiler defines the order of operation generated by three code addresses.

General representation :

x = y op z

Where x,b, or c represents temporary generated operations such as names, constants, or compiler, and op represents the operator.

Example

Given expression :

w := (-y * x) + (-y * z) 

The code with three addresses is as follows:

        t1 := -y

         t2 := x *t1

         t3 := -y

         t4 := z * t3

         t5 := t2 + t4

        w := t5

t  is used as registers in the target programme.

It is possible to represent the three address codes in two forms: quadruples and triples.

3.6.1 Quadruple & triples

Quadruple

For the implementation of the three address code, the quadruples have four fields. The quadruple field includes the name of the generator, the first operand source, the second operand source, and the output, respectively

Fig 6: Quadruple field

Example

w := -x * y + z 

The code with three addresses is as follows:

t1 := -x

t2 := y + z

t3 := t1 * t2

w := t3

These statements are expressed as follows by quadruples:

Triples

For the implementation of the three address code, the triples have three fields. The area of triples includes the name of the operator, the first operand of the source, and the second operand of the source.

The outcomes of the respective sub-expressions are denoted by the expression location in triples. Although describing expressions, Triple is equal to DAG.

Fig 7: Triples field

Example:

w := -x * y + z 

The three code addresses are as follows:

t1 := -x

t2 := y + zM

t3 := t1 * t2

w := t3   

Triples represent these statements as follows:

Key takeaway :

-         In quadruple, instruction is divided into 4 separate fields.

-         For the implementation of the three address code, the triples have three fields.

-         Triple does not use temporary variables.

3.7 Translation of assignment statements

The assignment statement in the syntax-directed translation deals primarily with expressions. This expression can be true, integer, array, and record form.

Consider the grammar :

S  →    id:= E 

E    →  E1 + E2 

E   →   E1 * E2 

E   →   (E1) 

E   →   id 

Here is the translation scheme for the grammar above:

●      The p returns an entry in the symbol table for the id.name.

●      The Emit feature is used to connect the three address codes to the output register. Otherwise, an error would be identified.

●      Newtemp() is a function for which new temporary variables are created.

●      E.place carries an E value.

Key takeaway :

-         The assignment statement in the syntax-directed translation deals primarily with expressions.

-         This expression can be true, integer, array, and record form.

3.8 Boolean expressions

There are two main uses of Boolean expressions. They are used in the estimation of logical values. They are often used when using if-then-else or while-do as a conditional expression.

Consider the grammar

E  →  E OR E 

E  →  E AND E 

E  →  NOT E  

E  →  (E) 

E →  id relop id 

E  →  TRUE 

E  →  FALSE 

The relop is denoted by <, >, <, >.

The AND and OR are still related. NOT has a higher precedent than AND and OR, ultimately.

To generate the three address codes, the EMIT function is used and the newtemp() function is used to generate the temporary variables.

The next state is found in the E →  id relop id2 and provides the index of the next three address statements in the output sequence.

Here is an example of how the three address code is created using the above translation scheme .

p>q AND r<s OR u>r 

     100: if p>q goto 103 

     101: t1:=0 

     102: goto 104 

     103: t1:=1 

     104: if r>s goto 107 

     105: t2:=0 

     106: goto 108 

     107: t2:=1 

     108: if u>v goto 111 

     109: t3:=0 

     110: goto 112 

     111: t3:= 1 

     112: t4:= t1 AND t2 

     113: t5:= t4 OR t3 

Key takeaway :

-         They are often used when using if-then-else or while-do as a conditional expression.

3.9 Statements that alter the flow of control

The goto declaration modifies the control stream. We need to specify a LABEL for a statement if we enforce Goto statements. To this end, an output may be added:

S →     LABEL: S 

    LABEL →     id

Semantic action is attached to this production device to record the Mark and its meaning in the symbol table.

The following grammar is used to integrate flow-of-control structure constructs:

S →  if E then S 

     S  →   if E then S else S 

     S →    while E do S 

     S →    begin L end 

     S→     A 

     L→    L; S 

     L →   S 

S is a statement here, L is a statement-list, A is an assignment statement, and E is an expression valued by Boolean.

Translation scheme  for the statement that alters the flow of controls

●      As in the case of Boolean expression grammar, we add the marker non-terminal M.

●      If so, this M is put before the statement in both. We need to put M before E in the case of while-do, as we need to return to it after executing S.

●      If we test E to be valid in the case of if-then-else, first S will be executed.

●      After this, we can make sure that the code after the if-then-else is executed instead of the second S. Then, after the first S, we put another non-terminal marker of N.

Grammar :

S →   if E then M S 

     S →    if E then M S else M S 

     S →    while M E do M S 

     S →    begin L end 

     S →    A 

     L→    L; M S 

     L →   S 

     M →    ∈ 

     N →    ∈ 

For this grammar, the translation scheme is as follows:

Key takeaway :

-         We need to specify a LABEL for a statement if we enforce Goto statements.

-         Most programming languages provide a standard collection of statements specifying the program's control flow.

3.10  Postfix translation

The translation rule of A.CODE in development A alpha consists of the concatenation of the translations of the CODE of the non-terminals in alpha in the same order as the non-terminals appear in alpha.

Postfix translation of while statement

Production

S   →  while M1 E do M2 S1

This can be measured as:

S →    C S1 

   C →    W E do 

   W →    while 

A perfect solution for transformation would be

Postfix translation of for statement

Production

S     for L = E1 step E2 to E3 do S1

This can be measured as:

F →    for L 

   T  →   F = E1 by E2 to E3 do 

   S  →   T S1 

Key takeaway:

-         To accomplish the postfix type, the output can be factored in.

-         The postfix notation is a sequential representation of the syntax tree.

3.11 Translation with a top-down parser

The top-down parsing technique parses the input and begins to construct a parse tree from the root node, moving progressively down to the leaf nodes.

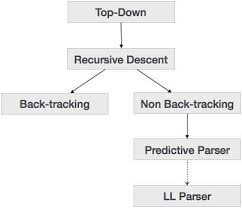
Fig 8: Procedures of top-down parser

Recursive Descent Parsing

A top-down parsing technique that builds the parse tree from the top and reads the input from left to right is recursive descent. For any terminal and non-terminal entity, it uses procedures. The input is recursively parsed by this parsing technique to make a parse tree, which may or may not require back-tracking.

But the related grammar (if not left-faced) does not prevent back-tracking. Predictive parsing is known as a form of recursive-descent parsing that does not require any back-tracking.

As it uses context-free grammar that is recursive, this parsing technique is called recursive.

Back-tracking

Top-down parsers start with the root node (start symbol) and match the production rules with the input string to replace them (if matched). Take the following CFG example to grasp this.

S → rXd | rZd

X → oa | ea

Z → ai

A top-down parser, for an input string: read, will function like this:

It will start with S from the rules of production and match its yield to the input's leftmost letter, i.e. 'r'. The very development of S (S→ rXd) corresponds to it. So the top-down parser progresses to the next letter of input (i.e. 'e'). The parser attempts to extend the 'X' non-terminal and verifies its output from the left  X,( x → oa). It does not fit the input symbol next to it.

So the backtracks of the top-down parser to obtain the next X, (X →ea) output guideline.

Now, in an ordered way, the parser matches all the input letters. The string has been approved

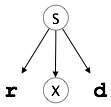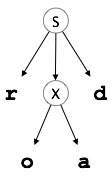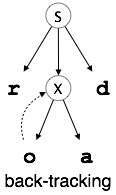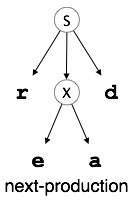Fig 9: Backtracking

Predictive Parser

The Predictive Parser is a recursive descent parser that can predict which output is to be used to replace the input string. Backtracking does not suffer from the predictive parser.

The predictive parser uses a look-ahead pointer to accomplish its functions, which points to the following input symbols. The predictive parser places certain restrictions on the grammar to make the parser back-tracking free and accepts only a grammar class known as LL(k) grammar.

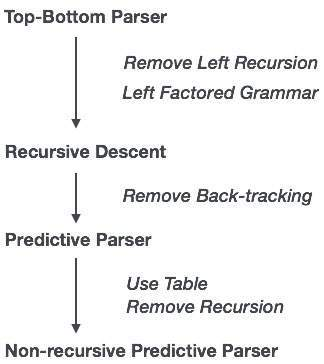
Fig 10:  top-bottom parser

In recursive descent parsing, for a single instance of input, the parser can have more than one output to choose from, while in the predictive parser, each stage has at most one production to choose from. There may be instances where the input string does not fit the production, making the parsing procedure fail.

LL Parser

LL grammar is approved by an LL Parser. To achieve simple implementation, LL grammar is a subset of context-free grammar but with certain constraints to get the simpler version.

The parser of LL is denoted as LLL (k). The first L in LL(k) parses the input from left to right, the second L in LL(k) is the left-most derivation, and the number of looks ahead is expressed by k itself. In general, k = 1, so LL(k) can also be written as LL(k) (1).

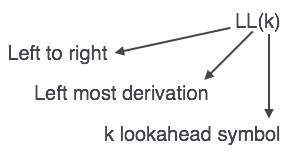
Fig 11: LL parser

Key takeaway :

-         Take input and begin to construct a parse tree from the root node, moving progressively down to the leaf nodes.

-         It uses procedures for every terminal and non - terminal entity.

-         Backtracking does not suffer from the predictive parser.

-         The Predictive Parser is a recursive descent parser

3.12 Array references in arithmetic expressions

●      Array elements can be accessed easily if elements are stored in a sequential position block.

●      Elements are numbered 0,1,.........,n-1(n elements ) for an array.

●      If the width of each element of an array is w, the ith element of array A starts at position

Base + i * w

Where base - relatively address, define storage allocation.

(base relatively addresses of A[0]  )

●      The array may be one- or two-dimensional.

For one - dimensional array :

A: array[low..high] of the ith elements is at: 

base + (i-low)*width → i*width + (base - low*width)

For multidimensional array :

Row major or column-major forms

Layout for the 2D array :

Fig 12: a two-dimensional array

Key takeaway :

-         Array elements can be accessed easily if elements are stored in a sequential position block.

3.13 Procedures call

❏      Procedure for a compiler is a significant and widely used programming construct. It is used to produce good code for calls and returns for processes.

❏      The run-time routines that manage the passing, calling, and returning of procedure arguments are part of the packages that support run-time.

Calling sequence :

A series of acts taken on entry and exit from each procedure is part of the translation for a call. In the calling sequence, the following actions take place:

●      When a procedure call occurs, space for the activation record is allocated.

●      Review the so-called method statement.

●      Develop environment pointers to allow data in enclosing blocks to be accessed by the named procedure.

●      Save the state of the calling process so that after the call it can restart execution.

●      Save the return address as well. It is the address of the place to which, after completion, the so-called routine must be moved.

●      Finally, the calling procedure creates a hop to the beginning of the code.

let us consider the grammar for a simple procedure call statement

●      S  call id (Elist)

●      Elist  Elist, E

●      Elist  E

For the procedure call, an appropriate transfer scheme would be:

In the procedure call, the queue is used to store a list of parameters.

Key takeaway :

-         It is used to produce good code for calls and returns for processes.

-         A series of acts taken on entry and exit from each procedure is part of the translation for a call.

3.14 Declarations and case statements

Declaration :

We need to layout storage for the declared variables when we encounter declarations.

You can manage declaration with a list of names as follows :

D T id ; D | ε

T B C | record ‘{‘D’}’

B int | float

C ε | [ num ] C

●      A declaration sequence is generated by Nonterminal D.

●      A fundamental, array, or record form is generated by nonterminal T.

●      One of the basic int or float types is generated by nonterminal B.

●      Nonterminal C produces a string of zero or more integers, each surrounded by brackets for "component".

We create an ST (Symbol Table) entry for every local name in a procedure, containing:

Production :

D →    integer, id 

   D  →   real, id 

   D  →   D1, id 

For declarations, an appropriate transformation scheme would be:

ENTER is used to enter the table of symbols and ATTR is used to trace the form of data.

Case statement  :

In some languages, the "switch" or "case" statement is available. The syntax for switch-statement is as shown below:

Switch-statement syntax s with expression

begin

   case value : statement

case value : statement

..

case value: statement

default: statement

end

There is a selector expression to be evaluated, followed by n constant values that may be taken by the expression, including a default value that, if no other value does, always matches the expression. Code to: is the intended translation of a turn.

1. Assess an expression.

2. Find which value is equivalent to the value of the expression in the list of cases.

3. Conduct the assertion that is correlated with the found meaning.

Find the following paragraph about the switch:

switch E

begin

case V1: S1

case V2: S2

case Vn-1: Sn-1

default: Sn

end

This case statement is translated into an intermediate code in the following form: Translation of a case statement.

code to analyze  E into t goto test

goto TEST 

                L1:         code for S1 

                              goto NEXT 

                L2:         code for S2 

                              goto NEXT 

                              . 

                              . 

                              . 

                Ln-1:      code for Sn-1 

                              goto NEXT 

                Ln:         code for Sn 

goto NEXT 

                TEST:      if T = V1 goto L1      

                               if T = V2 goto L2 

                               . 

                               . 

                               . 

                               if T = Vn-1 goto Ln-1 

                               goto  

NEXT: 

A new temporary T and two new label tests are created when the switch keyword is seen, and next.

When the case keyword happens, a new label Li is generated and inserted into the symbol table for each case keyword. A stack is put with the Vi value of each case constant and a pointer to this table-symbol entry.

Key takeaway :

-         We need to layout storage for the declared variables when we encounter declarations.

-         The case statement is unique because it contains an expression.

-         Process for switch - case statement

➢      Assess an expression.

➢      Find which value is equivalent to the value of the expression in the list of cases.

➢      Conduct the assertion that is correlated with the found meaning.

References: