Unit - 1

Introduction and Line Generation

1.1 Introduction

The more complex objects and operations are constructed by the primitives that are low-level objects or the operations from a higher level.

The primitives are the basic elements used in computer graphics.

Lines, curves, and polygons are the basic elements that are used to create complex graphical images on the computer.

The operations of basic primitives are used in a programming language.

To create any drawing on the computer these primitives are used as software.

To store the type of display the data is important.

1.2 Types of Computer Graphics

The meaningful information that can be represented in pictorial form on the computer is called graphics.

There are two types of computer graphics.

Raster Graphics:

The image in raster graphics is represented or drawn using pixels.

It is also known as a bitmap image.

The image is in a sequence of smaller pixels.

In short, the raster graphics shown image is a large number of pixels together.

Vector Graphics:

Vector graphics use mathematical formulae to draw different types of shapes, lines, objects, and so on.

The data in graphics are manipulated and represented graphically.

Key Takeaways:

There are two types of computer graphics as raster graphics and vector graphics.

Raster graphics displays the image in smaller pixels with a large number.

Whereas Vector graphics is that which uses the mathematical formulae to draw images.

1.3 Graphic Displays – Random Scan Displays, Raster Scan Displays, Frame Buffer, and Video Controller, Points, and Lines

1.3.1 Random Scan Displays

The electron beam is directed only to the area where the picture has to be drawn.

It is also called a vector display.

It draws the picture as one line at a time.

In any specified sequence, the picture line can be drawn or refresh.

For ex. Pen plotter

1.3.2 Raster Scan Displays

The raster scan display uses the CRT method.

It is based on television technology.

The electron beam in the raster scan sweeps from top to bottom by covering one row at a time.

The beam is intensity on and off is creating the pattern of the illuminated pattern of spots as it moves from each row.

The memory area is known as refresh buffer or frame buffer as it stores picture definition.

The memory area holds intensity values for all screen points.

1.3.3 Frame Buffer and Video Controller

Frame Buffer

The frame buffer is the video output device that drives a video display from the memory buffer as a complete set of data.

The images are stored in terms of a pixel by pixel.

The memory can be disc, integrated circuits, etc.

Video Controller

It is a key hardware component.

It is also known as a video or graphics card.

It allows the computer to generate graphics information for any video display device.

1.3.4 Points and Lines

Points: It is a basic element of computer graphics. It is completely defined by the pair of coordinates as (x, y).

Lines:

The line is the special build block of graphics it is used in various platforms such as line graphs, bar and pie charts, 2D and 3D graphs in mathematical function, engineering drawing, and architectural plans.

The straight line is developed in two ways as a structural method which shows the pixels that should be set before drawing the line and a conditional method that is used to find the pixels which should be set next.

Key Takeaways:

The graphic display is the things that are displayed in the graphics.

Points are the basic element in the graphic display.

Lines, raster scan display, random scan display, video controller, and frame buffer are the graphic displays that are usually used in graphics.

1.4 Line Drawing Algorithms

A line connects two points.

It is a basic element in graphics.

Two points are required to draw a line as X0, Y0, and X1, Y1.

1.4.1 Digital Differential Analyzer (DDA)

The digital differential analyzer (DDA) is a simple line generation algorithm.

The line connects two points.

Hence to draw any line we need at least two points.

Hence, we prefer one point as (X1, Y1) and the second point is (X2, Y2).

Following are some steps to perform the DDA algorithm.

Step 1: Get the input (X1, Y1) and (X2, Y2)

Step 2: Calculate the slope of the line using inputs.

M= Y2-Y1/X2-X1

Step 3: according to the slope of the line, we need to decide the case which gives the next point of the line.

Following are three cases are used to solve the DDA algorithm.

Case 1: m<1     Xn=X1+1       and         Yn=Y1+m

Case 2: m>1    Xn=X1+1/m   and        Yn=Y1+1

Case 3: m=1     Xn=X1+1        and      Yn=Y1+1

Step 4: the process continues till we get the input point (X2, Y2). Then the line generates with the help of coordinates that we occur.

Key Takeaways:

DDA is the line generation algorithm where the line connects two points.

Three cases are used to solve the line problems.

Cases are: m<1, m>1 and m=1

As the cases occurred the steps will be followed by case steps.

Example:

Inputs: (X1, Y1) = (0,0) and (X2, Y2) = (8,4)

M= Y2-Y1/X2-X1

 M=4-0/8-0 

M = 0.5

Here M=0.5

Hence follow case 1 where M<1 then Xn=X1+1       and         Yn=Y1+m

At last, we get the last point (X2, Y2) = (8,4) we stop.

1.4.2 Bresenham’s Line Drawing Algorithm

It is another line generation algorithm known as the incremental scan conversion algorithm.

It uses only integer calculations.

Following are steps to perform Bresenham’s algorithm.

Step 1: Get the input (X1, Y1) and (X2, Y2)

Step 2: Find decision parameter Pk and P0

Pk=2 ∆Y - ∆X

Where ∆X=X2-X1   and    ∆Y=Y2-Y1

Step 3: according to the value of Pk, we need to decide the case which gives the next point of the line.

Following are three cases are used to solve Bresenham’s algorithm.

Case 1: Pk>0, Pk+1=Pk + 2 ∆Y - 2 ∆X

Where Xn=X1+1   and Yn=Y1+1

Case 2: Pk<0, Pk+1=Pk + 2 ∆Y

Where Xn=X1+1   and Yn=Y1+1

Step 4: the process continues till we get the input point (X2, Y2). Then the line generates with the help of coordinates that we occur.

Key Takeaways:

Bresenham’s line generation is also known as the incremental scan conversion line generation algorithm.

It follows the integer calculations as given in the above steps.

Here are also some cases that calculates the value of Pk and follow some steps to reach the solution.

Example:

Step 1: Get the input (X1, Y1) and (X2, Y2)

(X1, Y1) = (20,10)    and (X2, Y2) = (30,18)

Step 2: find decision parameter Pk and P0

Pk=2 ∆Y - ∆X

Where ∆X=X2-X1=30-20=10 and    ∆Y=Y2-Y1=18-10=8

Hence, Pk=2 ∆Y - ∆X = 2*8-10= 16-10=6

At last, we get the last point (X2, Y2) = (30,18) we stop.

1.5 Circle Generating Algorithm

It is difficult to draw a circle than a line drawing.

The equation of a circle is r2=X2+Y2

There is some circle drawing algorithm as follows:

1.5.1 Digital Differential Analyzer (DDA) Circle Drawing Algorithm

This algorithm uses the incremental method to draw each point.

The algorithm calculates the starting point and by the value of E, the value of x and y coordinates will be increased and decreases respectively.

The equation of a circle is r2=X2+Y2

To calculate the value of E,

We have a formula,

2n-1<=r <=2n where r = radius of circle

E=2^-n=1/2^n

E is used to calculate the value of circle point which helps to draw a circle as

X2=X1+E Y1 for x and

Y2=Y1- E X2 for y

Algorithm:

Step 1: Read the radius r of the circle and calculate the value of E

Step 2: Start X=0 i.e., initial point and

              Start Y=r i.e., radius

Step 3: X1=0 and Y1=r

Step 4:

Do {

X2=X1+E Y1

Y2=Y1-E X2

//Here X2 represents Xn+1 and X1 represent Xn

//Xn is from the equation of a circle

Plot (int X2, int Y2)

//here swapping points to calculate next closest pixel

X1=X2

Y1=Y2

}

While ((Y1-Y0) < E or (X0-X1)>E)

//here, while the condition is to check the current position, is a starting point or not, if the current point is not starting point, then repeats.

Step 5: stop

Key Takeaways:

The circle generation having the DDA algorithm works the same as the DDA line generation algorithm.

By the formulae, it calculates the value of E and searches for the x and y coordinates i.e., point.

The point (x, y) can be increase or decrease in circle generation.

1.5.2 Bresenham’s Circle Drawing Algorithm

The following circle shows the 8 portions from which we will occur the coordinates of the circle.

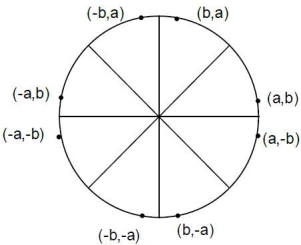
                               Fig. 1

Algorithm:

Step 1: input of circle radius r, (Xc, Yc)

Step 2: initial value X=0 and Y=r

Step 3: plot pixel (X+Xc, Y+Yc)

Step 4: decision parameter Pk=3-2r

Step 5: Start of the loop

If Case 1:

If Pk<0 then    Pk+1=Pk+4X+6

Where Xn=X+1 and Yn=Y

Else Case 2:

If Pk>0 then Pk+1=Pk+4(X-Y) +10

Xn=X+1   and Yn=Y-1

Step 6: X=Y stop

Key Takeaways:

Figure 1.5.2 shows the portion of the circle where 8 points are required to form a circle using bresenham’s algorithm.

Here are we need to calculate the value of Pk and then the cases occur.

As the case s as Pk<0 and Pk>0 suits the value of x and y coordinates are calculated.

Example:

Given R=10

Hence Y=R

If we want to draw a circle in the center then we have given the center points as (Xc, Yc) = (2,2)

Decision parameters are Pk and P0.

P0=3-2r

Here, P0=3-2*10=3-20=-17

Hence Pk=P0= -17

Following are two cases that will be decided according to Pk’s value.

Case 1:

If Pk<0 then    Pk+1=Pk+4X+6

Where Xn=X+1 and Yn=Y

Case 2:

If Pk>0 then Pk+1=Pk+4(X-Y) +10

Xn=X+1   and Yn=Y-1

Here X=Y then stop

1.6 Mid-Point Circle Generating Algorithm

Algorithm:

Step 1: input of circle radius r, (Xc, Yc)

Step 2: initial value X=0 and Y=r

Step 3: plot pixel (X+Xc, Y+Yc)

Step 4: decision parameter Pk=1-r

Step 5: Start of the loop

If Case 1:

If Pk<0 then    Pk+1=Pk+2X+1

Where Xn=X+1 and Yn=Y

Else Case 2:

If Pk>0 then Pk+1=Pk+2X+1-2Y

Xn=X+1   and Yn=Y-1

Step 6: X=Y stop

Key Takeaways:

It is also another method of generating the circle.

Here is also the radius of the circle is given the value of Pk is calculated by using the decision parameter formulae.

The cases are as follows with the value of Pk and (x, y) coordinate is calculated to generate a circle.

Example:

Given R=10

Hence Y=R

If we want to draw a circle in the center then we have given the center points as (Xc, Yc) = (2,2)

Decision parameters are Pk and P0.

P0=1-r

Here, P0=1-10=-9

Hence Pk=P0= -9

Following are two cases that will be decided according to Pk’s value.

Case 1:

If Pk<0 then    Pk+1=Pk+2X+1

Where Xn=X+1 and Yn=Y

Case 2:

If Pk>0 then Pk+1=Pk+2X+1-2Y

Xn=X+1   and Yn=Y-1

Now X=Y hence we stop the loop.

If we want to draw the circle at the center then we need coordinates as (Xc, Yc) Then coordinates becomes X=Xn+Xc and Y=Yn+Yc.

1.7 Parallel Version of these Algorithms

The parallelization is based on the line drawing and circle drawing algorithm.

The raster scan method is used to define the parallelization.

The line algorithm approaches a perfect speedup of P as the line length approaches infinity.

The circle algorithm approaches a speedup greater than 0.9 P as the circle radius approaches infinity.

Each algorithm shows the smaller setup over-head.

The three integer multiplies and one or two integer divides with seven loop iterations for line algorithm are used in the setup.

Four integer multiplies and no divides and one loop iteration are used in circle setup.

This parallelization process can be extended for other approaches in future work.

References:

1. Donald Hearn and M Pauline Baker, “Computer Graphics C Version”, Pearson Education

2. Foley, Vandam, Feiner, Hughes – “Computer Graphics principle”, Pearson Education.

3. Rogers, “Procedural Elements of Computer Graphics”, McGraw Hill

4. W. M. Newman, R. F. Sproull – “Principles of Interactive Computer Graphics” – Tata McGraw Hill.

5. Amrendra N Sinha and Arun D Udai,” Computer Graphics”, Tata McGraw Hill.

6. R.K. Maurya, “Computer Graphics” Wiley Dreamtech Publication.

7. M.C. Trivedi, NN Jani, Computer Graphics & Animations, Jaico Publications

8 Rishabh Anand, Computer Graphics- A practical Approach, Khanna Publishing House

9. Mukherjee, Fundamentals of Computer graphics & Multimedia, PHI Learning Private Limited.

10. Donald Hearn and M Pauline Baker, “Computer Graphics with OpenGL”, Pearson education