Unit – 1

Introduction

1.1 Introduction: Algorithms

Basically algorithms are the finite steps to solve problems in computers.

It can be the set of instructions that performs a certain task.

The collection of unambiguous instructions occurring in some specific sequence and such a procedure should produce output for a given set of input in a finite amount of time is known as Algorithm.

Algorithms are defined to be a step by step method to solve certain problems. For example if you need to write a program to calculate the age of a person let us say after 5 years so in programming  we need to take some input, process it and then provide an output.

Algorithm for the above scenario will be the steps used in order to calculate age after 5 years.

A simple algorithm for this scenario can be written as follow: -

Step 1: - Take the input as the current age of the person.

Step 2: - Perform the calculation i.e. add 5 years to his current age

Step 3: - Output will be a value obtained after calculation which is his age after 5 years.

An algorithm to be any well-defined computational procedure that takes some values as input and produces some values as output.

An algorithm is a finite set of instructions that, if followed, accomplishes a particular task. An algorithm is a sequence of unambiguous instructions for solving a problem, i.e., for obtaining a required output for any legitimate input in a finite amount of time.

Characteristics of algorithm

There are five main characteristics of an algorithm which are as follow:-

●      Input: - Any given algorithm must contain an input the format of the input may differ from one another based on the type of application, certain application needs a single input while others may need “n” inputs at initial state or might be in the intermediate state.

●      Output: - Every algorithm which takes the input leads to certain output. An application for which the algorithm is written may give output after the complete execution of the program or some of them may give output at every step.

●      Finiteness: - Every algorithm must have a proper end, this proper end may come after certain no of steps. Finiteness here can be in terms of the steps used in the algorithm or it can be in the term of input and output size (which should be finite every time).

●      Definiteness: - Every algorithm should define certain boundaries, which means that the steps in the algorithm must be defined precisely or clearly.

●      Effectiveness: - Every algorithm should be able to provide a solution which successfully solves that problem for which it is designed.

Analysis of the algorithm is the concept of checking the feasibility and optimality of the given algorithm, an algorithm is feasible and optimal if it is able to minimize the space and the time required to solve the given problem.

Key takeaway:

1. Basically, algorithms are the finite steps to solve problems in computers.
2. It can be the set of instructions that performs a certain task.
3. An algorithm is a sequence of unambiguous instructions for solving a problem.

1.2 Analyzing Algorithms

Donald Knuth developed the phrase "analysis of algorithms."

Algorithm analysis is a crucial aspect of computational complexity theory, as it provides a theoretical estimate of how much time and resources an algorithm will need to solve a given issue. The majority of algorithms are made to function with inputs of any length. The determination of the amount of time and space resources necessary to execute an algorithm is known as algorithm analysis.

Typically, an algorithm's efficiency or running time is expressed as a function linking the input length to the number of steps (time complexity) or the amount of memory (space complexity).

Needs for Analysis

By analyzing an algorithm for a specific problem, we can begin to create pattern recognition, allowing this algorithm to tackle similar types of problems.

Algorithms are frequently fairly distinct from one another, despite the fact that their goals are the same. We know, for example, that a set of numbers can be sorted using several algorithms. For the same input, the number of comparisons conducted by one algorithm may differ from that of others. As a result, the temporal complexity of those algorithms may vary. At the same time, we must determine how much RAM each algorithm requires.

The process of examining the algorithm's problem-solving capability in terms of the time and size required is known as algorithm analysis (the size of memory for storage while implementation). However, the most important consideration in algorithm analysis is the needed time or performance. In general, we conduct the following sorts of research:

Worst-case - The maximum number of steps that can be taken on any size instance.

Best-case- The smallest number of steps executed on any size instance.

Average case- The average number of steps executed on any size instance.

Amortized- A series of actions performed on a size input and averaged over time.

To solve a problem, we need to consider time as well as space complexity as the program may run on a system where memory is limited but adequate space is available or may be vice-versa. In this context, if we compare bubble sort and merge sort.

Bubble sorting does not require additional memory, but merge sort requires additional space. Though the time complexity of bubble sort is higher compared to merge sort, we may need to apply bubble sort if the program needs to run in an environment, where memory is very limited.

Key takeaway

1. Donald Knuth developed the phrase "analysis of algorithms."
2. Algorithm analysis is a crucial aspect of computational complexity theory, as it provides a theoretical estimate of how much time and resources an algorithm will need to solve a given issue.

1.3 Complexity of Algorithms

The phrase algorithm complexity refers to how many steps an algorithm must take to solve a particular problem. It calculates the order of the number of operations performed by an algorithm as a function of the size of the input data.

Instead of counting the actual steps, the order (approximation) of the count of operations is always considered when assessing the complexity.

The complexity of an algorithm is represented by the O(f) notation, which is often known as Asymptotic notation or "Big O" notation. The f in this case refers to a function with the same size as the input data. The asymptotic computation's complexity O(f) specifies the order in which resources like as CPU time, memory, and so on are utilized by the method, which is defined as a function of the size of the input data.

Complexity can be expressed in a variety of ways, including constant, logarithmic, linear, n*log(n), quadratic, cubic, exponential, and so on. It is simply the number of steps required to complete a certain algorithm in the sequence of constant, logarithmic, linear, and so on. To be even more specific, we often refer to an algorithm's complexity as "running time."

Complexities of an Algorithm

Constant Complexity:  It imposes an O level of complexity (1). It solves a given problem by doing a fixed number of steps, such as 1, 5, 10, and so on. The number of operations is unaffected by the size of the input data.

Logarithmic Complexity: It has an O(log(N)) level of complexity. It goes through a log(N)-step execution process. It is common to use the logarithmic basis of 2 when performing operations on N elements.

An algorithm having a complexity of O(log(N)) would go through 20 steps for N = 1,000,000. (With a constant precision). The logarithmic basis has little bearing on the operation count order in this case, hence it is frequently removed.

Linear Complexity: It imposes a level of O complexity (N). To execute an operation on N items, it contains the same number of steps as the entire number of elements.

If there are 500 items, for example, it will take roughly 500 steps. In a linear complexity problem, the number of items is proportional to the number of steps. For N elements, for example, the number of steps can be N/2 or 3*N.

Cubic Complexity: It imposes a level of O complexity (n3). It solves a given problem by performing N3 steps on N elements for N input data size.

Exponential Complexity: It has an O(2n), O(N! ), O(nk),... Complexity. It will execute the order of count of operations that is exponentially dependent on the size of the input data for N items.

Key takeaway

1. The phrase algorithm complexity refers to how many steps an algorithm must take to solve a particular problem.
2. It calculates the order of the number of operations performed by an algorithm as a function of the size of the input data.

1.4 Growth of Functions

The order of increase of an algorithm's running time, provides a straightforward characterization of its efficiency and also allows us to compare the relative performance of different algorithms. Merge sort, which has a worst-case running time of Θ(n lg n), surpasses insertion sort, which has a worst-case running time of Θ(n2).

Although we can sometimes calculate an algorithm's exact running time, the extra precision is usually not worth the work of computing it. The effects of the input size itself dominate the multiplicative constants and lower-order terms of an exact running time for large enough inputs.

We explore asymptotic efficiency of algorithms when we look at input sizes high enough to make simply the order of growth of the running time relevant. That is, we are interested in how an algorithm's running time varies with the size of the input in the limit, as the size of the input grows without bound. For all but the tiniest inputs, an asymptotically more efficient algorithm is usually the best option.

Asymptotic Notation

The notations we use to represent an algorithm's asymptotic running time are defined in terms of functions whose domains are the set of natural numbers N = 0 through N = n. These notations are useful for characterizing the worst-case running-time function T(n), which is normally only defined for integer input sizes.

However, there are instances when it is convenient to utilize asymptotic notation in a variety of ways. The notation, for example, can be simply extended to the domain of real numbers or restricted to a subset of natural numbers. However, it is critical to comprehend the specific meaning of the notation so that it is not misapplied.

Big Oh (O) Notation:

●      It is the formal way to express the time complexity.

●      It is used to define the upper bound of an algorithm’s running time.

●      It shows the worst case time complexity or largest amount of time taken by the algorithm to perform a certain task.

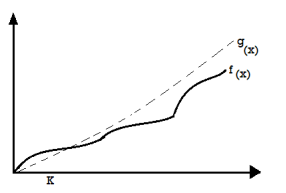
Fig 1: Big Oh notation

Here, f (n) <= g (n) ……………. (eq1)

Where n>= k, C>0 and k>=1

If any algorithm satisfies the eq1 condition then it becomes f (n)= O (g (n))

Big Omega (ῼ) Notation

●      It is the formal way to express the time complexity.

●      It is used to define the lower bound of an algorithm’s running time.

●      It shows the best case time complexity or best of time taken by the algorithm to perform a certain task.

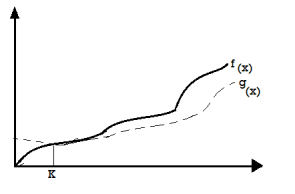
Fig 2: Big omega notation

Here, f (n) >= g (n)

Where n>=k and c>0, k>=1

If any algorithm satisfies the eq1 condition then it becomes f (n)= ῼ (g (n))

Theta (Θ) Notation

●      It is the formal way to express the time complexity.

●      It is used to define the lower as well as upper bound of an algorithm’s running time.

●      It shows the average case time complexity or average of time taken by the algorithm to perform a certain task.

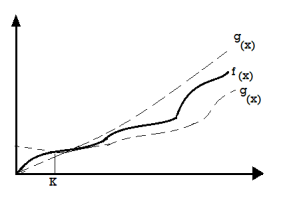
Fig 3: Theta notation

Let C1 g(n) be upper bound and C2 g(n) be lower bound.

C1 g(n)<= f (n)<=C2 g(n)

Where C1, C2>0 and n>=k

Key takeaway

1. The order of increase of an algorithm's running time, provides a straightforward characterization of its efficiency and also allows us to compare the relative performance of different algorithms.
2. Although we can sometimes calculate an algorithm's exact running time, the extra precision is usually not worth the work of computing it.
3. We explore asymptotic efficiency of algorithms when we look at input sizes high enough to make simply the order of growth of the running time relevant.

1.5 Performance Measurements

The general framework for analyzing the efficiency of algorithms could be the time and space efficiency.

Time efficiency indicates how fast an algorithm in question runs. Space efficiency deals with the extra space the algorithm requires.

Unit for measuring running time would be of primary consideration when estimating an algorithm’s performance is the number of basic operations required by the algorithm to process an input of a certain size.

The terms “basic operations” and “size” are both rather vague and depend on the algorithm being analyzed. Size is often the number of inputs processed.

For example, when comparing sorting algorithms, the size of the problem is typically measured by the number of records to be sorted. A basic operation must have the property that it’s time to complete does not depend on the particular values of its operands.

Adding or comparing two integer variables are examples of basic operations in most programming languages. Summing the contents of an array containing n integers is not, because the cost depends on the value of n (i.e., the size of the input).

Example: Consider a simple algorithm to solve the problem of finding the largest value in an array of n integers. The algorithm looks at each integer in turn, saving the position of the largest value seen so far. This algorithm is called the largest-value sequential search and is illustrated by the following Java function:

// Return position of largest value in "A"

Static int largest (int [] A) {

Int curlarge = 0; // Holds largest element position

For (int i=1; i<A.length; i++) // For each element

If (A[curlarge] < A[i])  // if A[i] is larger

Curlarge = i; // remember its position

Return curlarge; // Return largest position

}

Here, the size of the problem is n, the number of integers stored in A.

The basic operation is to compare an integer’s value to that of the largest value 60. It is reasonable to assume that it takes a fixed amount of time to do one such comparison, regardless of the value of the two integers or their positions in the array.

As the most important factor affecting running time is normally size of the input, for a given input size n we often express the time T to run the algorithm as a function of n, written as T(n). We will always assume T(n) is a non-negative value.

Let us call c the amount of time required to compare two integers in function largest. We do not care right now what the precise value of c might be. Nor are we concerned with the time required to increment variable i because this must be done for each value in the array, or the time for the actual assignment when a larger value is found, or the little bit of extra time taken to initialize curlarge.

We just want a reasonable approximation for the time taken to execute the algorithm. The total time to run largest is therefore approximately cn, because we must make n comparisons, with each comparison costing c time.

We say that function largest (and the largest-value sequential search algorithm in general) has a running time expressed by the equation

T(n) = cn.

This equation describes the growth rate for the running time of the largest value sequential search algorithm.

The growth rate for an algorithm is the rate at which the cost of the algorithm grows as the size of its input grows. Figure shows a graph for six equations, each meant to describe the running time for a particular program or algorithm.

A variety of growth rates representative of typical algorithms are shown. The two equations labeled 10n and 20n are graphed by straight lines. A growth rate of cn (for c any positive constant) is often referred to as a linear growth rate or running time.

This means that as the value of n grows, the running time of the algorithm grows in the same proportion. Doubling the value of n roughly doubles the running time. An algorithm whose running- time equation has a highest-order term containing a factor of n2 is said to have a quadratic growth rate.

In Figure, the line labeled 2n2 represents a quadratic growth rate. The line labeled 2n represents an exponential growth rate. This name comes from the fact that n appears in the exponent. The line labeled n! is also growing exponentially.

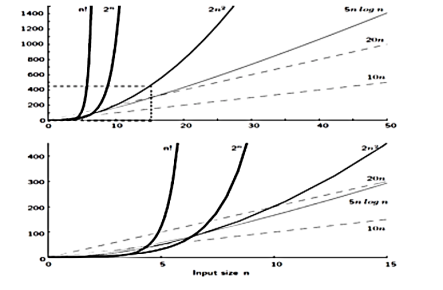
Fig 4:  Two views of a graph illustrating the growth rates for six equations.

The bottom view shows in detail the lower-left portion of the top view. The horizontal axis represents input size. The vertical axis can represent time, space, or any other measure of cost.

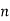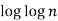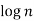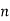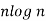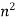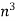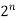16	2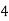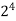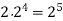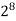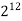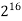
256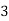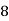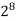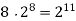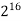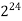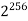
1024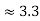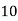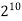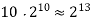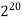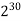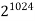
64K		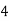		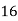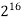16 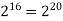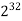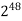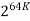
1M	≈4.3	20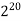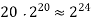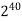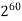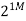
1G	≈4.9	30		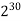3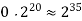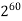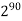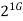

Fig 5: Costs for growth rates representative of most computer algorithms.

Both time and space efficiencies are measured as functions of the algorithm's input size.

Time efficiency is measured by counting the no. Of times the algorithm’s basic operation is executed. Space efficiency is measured by counting the number of extra memory units consumed by the algorithm.

The efficiencies of some algorithms may differ significantly for inputs of the same size. For such algorithms, one has to distinguish between the worst case, average case and best case efficiencies.

The framework’s primary interest lies in the order of growth of the algorithm’s running time as its input size goes to infinity.

Key takeaway

1. The general framework for analyzing the efficiency of algorithm could be the time and space efficiency.
2. Time efficiency indicates how fast an algorithm in question runs. Space efficiency deals with the extra space the algorithm requires.
3. The terms “basic operations” and “size” are both rather vague and depend on the algorithm being analyzed.

1.6 Sorting and Order Statistics - Shell Sort

Shell sort is a sorting algorithm that is based on the insertion sort algorithm and is very efficient. When the smaller value is on the far right and must be pushed to the far left, this technique avoids huge shifts as in insertion sort.

This algorithm sorts widely spaced elements first, then sorts the less widely spaced elements using insertion sort.  Interval is the name for this spacing.  This interval is calculated using Knuth's formula, which is as follows:

Knuth's Formula

h = h * 3 + 1

Where −

h is interval with initial value 1

Because the average and worst-case complexity of this technique relies on the gap sequence, the best known is O(n), where n is the number of items, it is relatively efficient for medium-sized data sets. The worst-case scenario for spatial complexity is O(n).

Algorithm

Shell_Sort(Arr, n)

Time complexity

Best case - Ω(n log(n))

Average case - θ(n log(n)2)

Worst case - O(n log(n)2)

Space complexity

Worst case - O(1)

Key takeaway

1. Shell sort is a sorting algorithm that is based on the insertion sort algorithm and is very efficient.
2. When the smaller value is on the far right and must be pushed to the far left, this technique avoids huge shifts as in insertion sort.

1.7 Quick Sort

Quick sort algorithm works on the pivot element.

● Select the pivot element (partitioning element) first. Pivot element can be random number from given unsorted array.

● Sort the given array according to pivot as the smaller or equal to pivot comes into left array and greater than or equal to pivot comes into right array.

● Now select the next pivot to divide the elements and sort the sub arrays recursively.                                                                                                                                      

Features

● Developed by C.A.R. Hoare

●  Efficient algorithm

● NOT stable sort

●  Significantly faster in practice, than other algorithms    

Algorithm

ALGORITHM Quicksort (A[ l …r ])

//sorts by quick sort

//i/p: A sub-array A[l..r] of A[0..n-1],defined by its left and right indices l and r //o/p: The sub-array A[l..r], sorted in ascending order

If l < r

Partition (A[l..r]) // s is a split position

Quicksort(A[l..s-1])

Quicksort(A[s+1..r]

ALGORITHM Partition (A[l ..r])

//Partitions a sub-array by using its first element as a pivot

//i/p: A sub-array A[l..r] of A[0..n-1], defined by its left and right indices l and r (l <r)

//o/p: A partition of A[l..r], with the split position returned as this function‘s value p→A[l]

i→l

j→r + 1;

Repeat

Repeat i→i + 1 until A[i] >=p  //left-right scan

Repeat j→j – 1 until A[j] < p  //right-left scan

If (i < j)   //need to continue with the scan

Swap(A[i], a[j])

Until i >= j   //no need to scan

Swap(A[l], A[j])

Return j

Analysis of Quick Sort Algorithm  

1. Best case: The pivot which we choose will always be swapped into the exactly the middle of the list. And also consider pivot will have an equal number of elements both to its left and right sub arrays.
2. Worst case: Assume that the pivot partition the list into two parts, so that one of the partition has no elements while the other has all the other elements.
3. Average case: Assume that the pivot partition the list into two parts, so that one of the partition has no elements while the other has all the other elements.

Key takeaways

1. Quick sort algorithm works on the pivot element.
2. Select the pivot element (partitioning element) first. Pivot element can be a random number from a given unsorted array.
3. Sort the given array according to pivot as the smaller or equal to pivot comes into the left array and greater than or equal to pivot comes into the right array.

1.8 Merge Sort

Merge sort consisting two phases as divide and merge.

● In divide phase, each time it divides the given unsorted list into two sub list until each sub list get single element then sorts the elements.

● In merge phase, it merges all the solution of sub lists and find the original sorted list.

Features:

● Is an algorithm dependent on comparison?

● A stable algorithm is

● A fine example of the strategy of divide & conquer algorithm design

● John Von Neumann invented it.

Steps to solve the problem:

Step 1: If the length of the given array is 0 or 1 then it is already sorted, else follow step 2.

Step 2: Split the given unsorted list into two half parts

Step 3: Again, divide the sub list into two parts until each sub list get single element

Step 4: As each sub list gets the single element compare all the elements with each other & swap in between the elements.

Step 5: Merge the elements same as divide phase to get the sorted list

Algorithm:

ALGORITHM Mergesort ( A[0… n-1] )

//sorts array A by recursive mergesort

//i/p: array A

//o/p: sorted array A in ascending order

If n > 1

Copy A[0… (n/2 -1)] to B[0… (n/2 -1)]

Copy A[n/2… n -1)] to C[0… (n/2 -1)]

Mergesort ( B[0… (n/2 -1)] )

Mergesort ( C[0… (n/2 -1)] )

Merge ( B, C, A ) 

ALGORITHM Merge ( B[0… p-1], C[0… q-1], A[0… p+q-1] )

//merges two sorted arrays into one sorted array

//i/p: arrays B, C, both sorted

//o/p: Sorted array A of elements from B & C

I →0

j→0

k→0

While i < p and j < q do

If B[i] ≤ C[j]

A[k] →B[i]

i→i + 1

Else

A[k] →C[j]

j→j + 1

k→k + 1

If i == p

Copy C [ j… q-1 ] to A [ k… (p+q-1) ]

Else

Copy B [ i… p-1 ] to A [ k… (p+q-1) ]

Example:

Apply merge sort for the following list of elements: 38, 27, 43, 3, 9, 82, 10

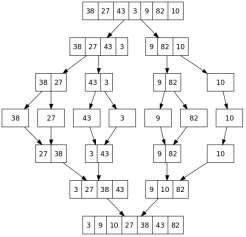
Analysis of merge sort:

All cases having same efficiency as: O (n log n)

T (n) =T ( n / 2 ) + O ( n )

T (1) = 0

Space requirement: O (n) 

Advantages

●  The number of comparisons carried out is almost ideal.

●  Merge sort is never going to degrade to O (n2)

●  It is applicable to files of any size.

Limitations

●  Using extra memory O(n).

Key takeaways

1. Merge sort consisting two phases as divide and merge.
2. In divide phase, each time it divides the given unsorted list into two sub list until each sub list get single element then sorts the elements.
3. In merge phase, it merges all the solution of sub lists and find the original sorted list.

1.9 Heap Sort

Heap Sort is one of the best in-place sorting strategies with no worst-case quadratic runtime. Heap sort requires the creation of a Heap data structure from the specified array and then the use of the Heap to sort the array.

You should be wondering how it can help to sort the array by converting an array of numbers into a heap data structure. To understand this, let's begin by knowing what a heap is.

Heap is a unique tree-based data structure that meets the following special heap characteristics:

1. Shape property: The structure of Heap data is always a Complete Binary Tree, which means that all tree levels are fully filled.

2. Heap property: Every node is either greater or equal to, or less than, or equal to, each of its children. If the parent nodes are larger than their child nodes, the heap is called Max-Heap, and the heap is called Min-Heap if the parent nodes are smaller than their child nodes.

The Heap sorting algorithm is split into two basic components:

●  Creating an unsorted list/array heap.

●  By repeatedly removing the largest/smallest element from the heap, and inserting it into the array, a sorted array is then created.

Complexity analysis of heap sort

Time complexity:

●  Worst case: O (n*log n)

●  Best case: O (n*log n)

●  Average case: O (n*log n)

Space complexity: O (1)

Key takeaway:

1. Heap Sort is one of the best in-place sorting strategies with no worst-case quadratic runtime.
2. Heap Sort is very fast and for sorting it is widely used.
3. Heap sorting is not a stable type, and requires constant space to sort a list.

1.10 Comparison of Sorting Algorithms

Based on a comparison, Bubble sort, selection sort, insertion sort, Merge sort, quicksort, heap sort, and other sorting techniques are examples. Because the values are compared and placed into sorted positions in different phases, these techniques are referred to as comparison-based sorting. We'll look at the time complexity of various strategies here.

Some sorting algorithms are not dependent on comparison. Radix sort, bucket sort, and count sort are a few examples. Because two elements are not compared while sorting, this is a non-comparison-based sort. The methods are a little different. Now we'll look at the differences between them using various types of analysis.

Other parameters might be used to compare sorting strategies. In-place sorting algorithms and out-place sorting algorithms are two types of sorting algorithms. In-place sorting algorithms are those that do not require any additional storage space. Quicksort and heapsort algorithms, for example, are available. Merge sort, on the other hand, is an out-of-place sorting algorithm.

Some algorithms are available online, while others are not. The term "online sorting algorithm" refers to a sorting algorithm that accepts additional elements while the sorting process is in progress.

Key takeaway

1. Based on a comparison, Bubble sort, selection sort, insertion sort, Merge sort, quicksort, heap sort, and other sorting techniques are examples.
2. Because the values are compared and placed into sorted positions in different phases, these techniques are referred to as comparison-based sorting.

1.11 Sorting in Linear Time

We have sorting algorithms that take O (n log n) time to sort "n" numbers.

In the worst situation, Merge Sort and Heap Sort achieve this upper constraint, whereas Quick Sort accomplishes it in the average case.

The sorted order established by the Merge Sort, Quick Sort, and Heap Sort algorithms is based only on comparisons between the input components. "Comparison Sort" is the name given to such a sorting method.

Some algorithms, such as Counting Sort, Radix Sort, and Bucket Sort, are faster and take linear time, but they require a special assumption about the input sequence to sort.

The input for Counting Sort and Radix Sort is assumed to be an integer in a limited range. Bucket Sort assumes that the input is generated by a random process that distributes elements uniformly over the interval.

Counting sort

The input for Counting Sort and Radix Sort is assumed to be an integer in a limited range.

Bucket Sort assumes that the input is generated by a random process that distributes elements uniformly over the interval.

Counting Sort uses three arrays:

1. A [1, n] holds initial input.
2. B [1, n] holds sorted output.
3. C [1, k] is the array of integer. C [x] is the rank of x in A where x ∈ [1, k]

Firstly C [x] to be a number of elements of A [j] that is equal to x

We set B[C [x]] =A[j]

Counting Sort (array P, array Q, int k) 

1. For i ← 1 to k 

2. Do C [i] ← 0     [ θ(k) times] 

3. For j  ← 1 to length [A] 

4. Do C[A[j]] ← C [A [j]]+1    [θ(n) times] 

5. // C [i] now contain the number of elements equal to i 

6. For i  ← 2 to k 

7. Do C [i]  ←  C [i] + C[i-1] [θ(k) times] 

8. //C[i] now contain the number of elements ≤ i 

9. For j ← length [A] down to 1 [θ(n) times] 

10. Do B[C[A[j]  ←  A [j] 

11. C[A[j]  ←  C[A[j]-1 

Bucket sort

On average, Bucket Sort takes linear time. Bucket Sort, like Counting Sort, is quick since it takes into account the input. Bucket Sort assumes the input is created by a random process that evenly distributes elements over the interval [0,1].

Bucket Sort is used to sort n input numbers.

●      Partition into n buckets, which are non-overlapping intervals.

●      Each input number is assigned to one of the buckets.

●      Each bucket is sorted using a basic algorithm, such as Insertion Sort, and

●      Then the sorted lists are concatenated.

The input to Bucket Sort is an n-element array A, and each element A I in the array must satisfy 0≤A [i] <1. The method relies on an auxiliary array B [0....n-1] of linked lists (buckets) and assumes that such lists are maintained by a mechanism.

BUCKET-SORT (A)

1. n ← length [A]

2. For i ← 1 to n

3. Do insert A [i] into list B [n A[i]]

4. For i ← 0 to n-1

5. Do sort list B [i] with insertion sort.

6. Concatenate the lists B [0], B [1] ...B [n-1] together in order.

Key takeaway

1. The sorted order established by the Merge Sort, Quick Sort, and Heap Sort algorithms is based only on comparisons between the input components.
2. "Comparison Sort" is the name given to such a sorting method.
3. The input for Counting Sort and Radix Sort is assumed to be an integer in a limited range.
4. On average, Bucket Sort takes linear time. Bucket Sort, like Counting Sort, is quick since it takes into account the input.

References:

1. Thomas H. Coreman, Charles E. Leiserson and Ronald L. Rivest, “Introduction to Algorithms”, Printice Hall of India.

2. E. Horowitz & S Sahni, "Fundamentals of Computer Algorithms",

3. Aho, Hopcraft, Ullman, “The Design and Analysis of Computer Algorithms” Pearson Education, 2008.

4. LEE "Design & Analysis of Algorithms (POD)", McGraw Hill

5. Richard E.Neapolitan "Foundations of Algorithms" Jones & Bartlett Learning