Unit – 1
Introduction to semiconductor physics
We know that in classical physics a particle is well localized in space. We can calculate its position and velocity simultaneously.
But for quantum mechanics, a particle is not well localized in space. We cannot calculate its position and velocity simultaneously.
In Quantum mechanics it is describe that the matter wave associated with the particle. Wave functions depend on the whole space. Hence, they cannot be localized.
If the wave function is made to vanish everywhere except in the neighbourhood of the particle or the neighbourhood of the classical trajectory, it can then be used to describe the dynamics of the particle. That is a particle which is localized within a certain region of space can be described by a matter wave whose amplitude is large in that region and zero outside it. This matter wave must then be localized around the region of space within which the particle is confined.
A localized wave function is called a Wave Packet or Wave Group. A wave packet or wave group therefore consists of a group of waves of slightly different wavelengths with phases and amplitudes so chosen that they interfere constructively over a small region of space and destructively elsewhere.
Wave packets are Not only useful in the explanation of isolated particles that are confined to a certain spatial region but they also play a key role in understanding the connection between quantum mechanics and classical mechanics. The wave packet concept also represents a uniting mathematical tool that describes particle-like behaviour and also its wave-like behaviour.
Phase and group velocity are two important and related concepts in wave mechanics. They arise in quantum mechanics in the time development of the state function for the continuous case, i.e., wave packets.
According to the theory of relativity particle velocity (v) is always less than the speed of light c. But according to the De-Broglie wave velocity must be greater than c. This is an unexpected result. According to this the de-Broglie wave associated with the particle would travel faster than the particle itself thus leaving the particle far behind.
The difficulty was recovered by Schrodinger. He proposed that a material particle in motion is equivalent to a wave packet rather than a single wave. Wave packet comprises of a group of waves, each with slightly different velocity and wavelength.
Such a wave packet moves with its own velocity vg called the group velocity.
The individual wave forming the wave packet possesses an average velocity vp called the phase velocity.
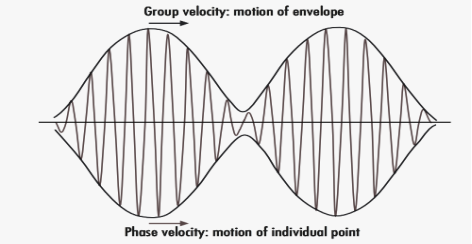
Figure: Wave Packet
It can be shown that the velocity of the material particle v is the same as group velocity
Let us assume two wave trains have same amplitude but different frequency and phase velocities
u (x, t) =A sin (ωt - kx) …….(1)
u’ (x, t) =A sin[(ω+∆ω) t-(k+∆k) x] …….(2)
Where ω and (ω+Δω) are angular frequencies and k and (k +Δk) are propagation constants
The superposition of two waves is of the form
ψ(x,t) = u +u’ = A sin(ωt - kx)sin[(ω+∆ω)t - (k+∆k)x] …….(3)
As Δ ω and Δk are small therefore (ω+Δω) 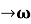 and (k + Δk)
and (k + Δk) 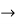 k, equation (3) reduces to
k, equation (3) reduces to
Ψ (x,t) = 2Acos[ 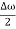 t -
t -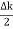 x] sin(ωt - kx) .…….(4)
x] sin(ωt - kx) .…….(4)
This equation represents a vibration of amplitude
2Acos [ 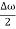 t -
t -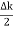 x] …….(5)
x] …….(5)
The phase of the resultant wave moves with the velocity known as phase velocity
vp= 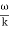 ……..(6)
……..(6)
And the amplitude moves with the velocity known as group velocity
vg =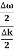 =
= 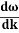
vg = 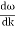 ….….(7)
….….(7)
Key Takeaways
- A localized wave function is called a Wave Packet or Wave Group. A wave packet or wave group therefore consists of a group of waves of slightly different wavelengths with phases and amplitudes so chosen that they interfere constructively over a small region of space and destructively elsewhere.
Wave packet moves with its own velocity vg called the group velocity. vg = 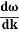
The individual wave forming the wave packet possesses an average velocity vp called the phase velocity. vp= 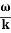
WAVE FUNCTION; PHYSICAL INTERPRETATION OF WAVE FUNCTION
Quantum theory and determinism usually do not go together. A natural combination is quantum theory and randomness. Indeed, when in the end of 19th century physics seemed to be close to provide a very good deterministic explanation of all observed phenomena, Lord Kelvin identified “two clouds” on “the beauty and clear-ness of the dynamical theory”. One of this “clouds” was the quantum theory which brought a consensus that there is randomness in physics. Recently we even “certify” randomness using quantum experiments
The quantum theory of the wave function of the Universe is a very successful deterministic theory fully consistent with our experimental evidence. However, it requires accepting that the world we experience is only part of the reality and there are numerous parallel worlds. The existence of parallel worlds allows us to have a clear deterministic and local physical theory.
Wave Function
The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x.
The wave function ψ associated with a moving particle is not an observable quantity and does not have any direct physical meaning. It is a complex quantity. The complex wave function can be represented as
ψ(x, y, z, t) = a + ib
And its complex conjugate as
ψ*(x, y, z, t) = a – ib.
The product of wave function and its complex conjugate is
ψ(x, y, z, t)ψ*(x, y, z, t) = (a + ib) (a – ib) = a2 + b2
a2 + b2 is a real quantity.
However, this can represent the probability density of locating the particle at a place in a given instant of time.
The positive square root of ψ (x, y, z, t) ψ*(x, y, z, t) is represented as |ψ (x, y, z, t), called the modulus of ψ. The quantity |ψ (x, y, z, t) |2 is called the probability. This interpretation is possible because the product of a complex number with its complex conjugate is a real, non-negative number.
We should be able to find the particle somewhere, we should only find it at one place at a particular instant, and the total probability of finding it anywhere should be one.
For the probability interpretation to make sense, the wave function must satisfy certain conditions.
- The wave function must be single valued at each point.
- The probability of finding the particle at time t in an interval ∆x must be some number between 0 and 1.
- ψ must be finite everywhere.
- ψ must be continuous everywhere and
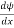 must also be continuous everywhere except where V(x) is infinite.
must also be continuous everywhere except where V(x) is infinite. - ψ (x) must vanish ψ
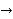 0 as x
0 as x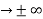 .
. - The wave function should satisfy the normalization condition. Normalization condition of a wave function ψ is mathematical statement of existence of the particle somewhere. So that if we sum up all possible values ∑|ψ(xi,t)|2∆xi we must obtain 1. The total probability of finding the particle anywhere must be one. Normalization condition is given as
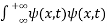 dx =1
dx =1
Only wave function with all these properties can yield physically meaningful result.
Physical significance of wave function
- The wave function ‘Ѱ’ has no physical meaning. It is a complex quantity representing the variation of a matter wave.
- The wave function Ѱ(r,t) describes the position of particle with respect to time .
- It can be considered as ‘probability amplitude’ since it is used to find the location of the particle.
- The square of the wave function gives the probability density of the particle which is represented by the wave function itself.
- More the value of probability density, more likely to find the particle in that region.
The Schrodinger equation also known as Schrodinger’s wave equation is a partial differential equation that describes the dynamics of quantum mechanical systems by the wave function. The trajectory, the positioning, and the energy of these systems can be retrieved by solving the Schrodinger equation.
All of the information for a subatomic particle is encoded within a wave function. The wave function will satisfy and can be solved by using the Schrodinger equation. The Schrodinger equation is one of the fundamental axioms that are introduced in undergraduate physics.
Statistical Interpretation
It is not possible to measure all properties of a quantum system precisely. Max Born suggested that the wave function was related to the probability that an observable has a specific value.
In any physical wave if ‘A’ is the amplitude of the wave, then the energy density i.e., energy per unit volume is equal to ‘A2’. Similar interpretation can be made in case of mater wave also. In matter wave, if ‘Ψ ‘is the wave function of matter waves at any point in space, then the particle density at that point may be taken as proportional to ‘Ψ2’. Thus, Ψ2 is a measure of particle density.
According to Max Born ΨΨ*=Ψ2 gives the probability of finding the particle in the state ‘Ψ’. i.e., ‘Ψ2’ is a measure of probability density. The probability of finding the particle in a volume (dv=dx dy dz) is given by
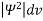 =
= 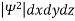
Since the particle has to be present somewhere, total probability of finding the particle somewhere is unity i.e., particle is certainly to be found somewhere in space. i.e.
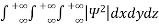 =1
=1
Or 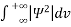 =1
=1
This condition is called Normalization condition. A wave function which satisfies this condition is known as normalized wave function.
The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ (x, t) |2 as a probability density, a probability per unit length of finding the particle at a time t at position x.
Key Takeaways
- The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable.
- The wave function must be single valued at each point. The probability of finding the particle at time t in an interval ∆x must be some number between 0 and 1. ψ must be finite everywhere.
- According to Max Born ΨΨ*=Ψ2 gives the probability of finding the particle in the state ‘Ψ’. i.e., ‘Ψ2’ is a measure of probability density. The probability of finding the particle in a volume (dv=dxdydz) is given by
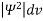 =
= 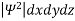
SCHRODINGER’S TIME DEPENDENT WAVE EQUATION; TIME INDEPENDENT WAVE EQUATION
Schrodinger wave equation, is the fundamental equation of quantum mechanics, same as the second law of motion is the fundamental equation of classical mechanics. This equation has been derived by Schrodinger in 1925 using the concept of wave function on the basis of de-Broglie wave and plank’s quantum theory.
Let us consider a particle of mass m and classically the energy of a particle is the sum of the kinetic and potential energies. We will assume that the potential is a function of only x.
So, we have
E= K+V = mv2+V(x) =
mv2+V(x) =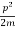 +V(x) ……….. (1)
+V(x) ……….. (1)
By de Broglie’s relation we know that all particles can be represented as waves with frequency ω and wave number k, and that E= ℏω and p= ℏk.
Using this equation (1) for the energy will become
ℏω = 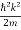 + V(x) ……….. (2)
+ V(x) ……….. (2)
A wave with frequency ω and wave number k can be written as usual as
Ψ (x, t) =Aei(kx−ωt) ……….. (3)
The above equation is for one dimensional and for three dimensional we can write it as
ψ (r, t) =Aei(k·r−ωt) ……….. (4)
But here we will stick to one dimension only.
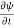 =−iωψ ⇒ ωψ=
=−iωψ ⇒ ωψ=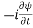 ……….. (5)
……….. (5)
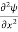 =−k2ψ ⇒ k2ψ = -
=−k2ψ ⇒ k2ψ = - 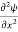 ……….. (6)
……….. (6)
If we multiply the energy equation in Eq. (2) by ψ, and using(5) and (6) , we obtain
ℏ(ωψ) = 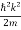 ψ+ V(x) ψ ⇒
ψ+ V(x) ψ ⇒ 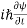 = -
= - 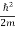
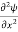 + V(x) ψ ……….. (7)
+ V(x) ψ ……….. (7)
This is the time-dependent Schrodinger equation.
If we put the x and t in above equation then equation (7) takes the form as given below
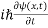 = -
= - 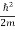
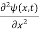 + V(x) ψ(x,t) ……….. (8)
+ V(x) ψ(x,t) ……….. (8)
In 3-D, the x dependence turns into dependence on all three coordinates (x, y, z) and the 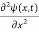 term becomes ∇2ψ.
term becomes ∇2ψ.
The term |ψ(x)|2 gives the probability of finding the particle at position x.
Let us again take it as simply a mathematical equation, then it’s just another wave equation. However, we already know the solution as we used this function ψ (x, t) =Aei(kx−ωt) to produce Equations (5), (6) and (7)
But let’s pretend that we don’t know this, and let’s solve the Schrodinger equation as if we were given to us. As always, we will guess an exponential solution by looking at exponential behaviour in the time coordinate, our guess is ψ (x, t) =e−iωtf(x) putting this into Equation (7) and cancelling the e−iωt yields
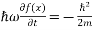
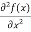 + V(x) f(x) ……….. (9)
+ V(x) f(x) ……….. (9)
We already know that E=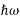 . However, ψ (x, t) is general convention to also use the letter ψ to denote the spatial part. So, we will now replace f(x) with ψ(x)
. However, ψ (x, t) is general convention to also use the letter ψ to denote the spatial part. So, we will now replace f(x) with ψ(x)
Eψ = - 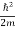
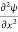 + V(x) ψ ……….. (10)
+ V(x) ψ ……….. (10)
This is called the time-independent Schrodinger equation.
Key Takeaways
- Schrodinger wave equation, is the fundamental equation of quantum mechanics
- The time-dependent Schrodinger equation is given by
⇒ 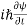 = -
= - 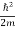
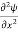 + V(x) ψ
+ V(x) ψ
- The time-independent Schrodinger equation is given by
Eψ = - 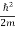
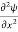 + V(x) ψ
+ V(x) ψ
Let us consider a particle of mass ‘m’ in a deep well restricted to move in a one dimension (say x). Let us assume that the particle is free inside the well except during collision with walls from which it rebounds elastically.
The potential function is expressed as
V= 0 for 0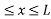 ………. (1)
………. (1)
V= 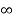 for x <0, x>L ………. (2)
for x <0, x>L ………. (2)
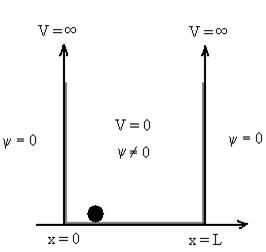
Figure: Particle in deep potential well
The probability of finding the particle outside the well is zero (i.e. Ѱ =0)
Inside the well, the Schrödinger wave equation is written as
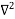 ψ +
ψ +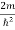 E ψ =0 …………….(2)
E ψ =0 …………….(2)
Substituting 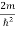 E = k2 …………….(3)
E = k2 …………….(3)
Writing the SWE for 1-D we get
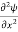 + k2 ψ =0 …………….(4)
+ k2 ψ =0 …………….(4)
The general equation of above equation may be expressed as
ψ = Asin (kx + ϕ) …………….(5)
Where A and ϕ are constants to be determined by boundary conditions
Condition I: We have ψ = 0 at x = 0, therefore from equation
0 = A sinϕ
As A 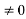 then sinϕ =0 or ϕ=0 …………….(6)
then sinϕ =0 or ϕ=0 …………….(6)
Condition II: Further ψ = 0 at x = L, and ϕ=0, therefore, from equation (5)
0 = Asin kL
As A 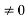 then sinkL =0 or kL=nπ
then sinkL =0 or kL=nπ
k = 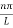 …………….(7)
…………….(7)
Where n= 1,2,3,4………
Substituting the value of k from (7) to (3)
)2 = 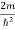 E
E
This gives energy of level
En = 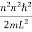 n=1,2,3,4…so on …………….(8)
n=1,2,3,4…so on …………….(8)
From equation En is the energy value (Eigen Value) of the particle in a well.
It is clear that the energy values of the particle in well are discrete not continuous.
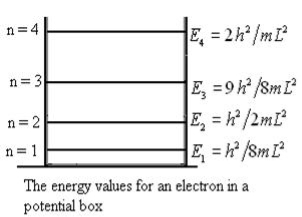
Figure: The energy values for an electron in a potential box
Using (6) and (7) equation (5) becomes, the corresponding wave functions will be
ψ = ψn = Asin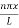 …………….(9)
…………….(9)
The probability density
|ψ(x,t)|2 = ψ ψ*
|ψ(x,t)|2 = A2sin2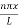 …………….(10)
…………….(10)
The probability density is zero at x = 0 and x = L. Since the particle is always within the well
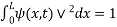 …………….(11)
…………….(11)
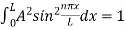
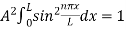
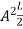 =1
=1
A = 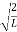
Substituting A in equation (9) we get
ψ = ψn = 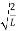 sin
sin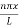 n=1,2,3,4….. …………….(12)
n=1,2,3,4….. …………….(12)
The above equation (12) is normalized wave function or Eigen function belonging to energy value En
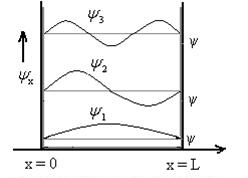
Figure: Wave function for Particle
The allowed wave functions for an electron trapped in a one dimensional potential box
Key Takeaways
- It is assumed that the particle is free inside the well except during collision with walls from which it rebounds elastically.
- The probability of finding the particle outside the well is zero (i.e Ѱ =0)
- The energy values of the particle in well are discrete not continuous and Energy of level is given by
- En =
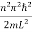 n=1,2,3,4…so on
n=1,2,3,4…so on - The probability density is given by
- |ψ(x,t)|2 = A2sin2
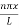
The KP model is a single-electron problem. The electron moves in a one-dimensional crystal of length L. The periodic potential that the electrons experience in the crystal lattice is approximated by the following periodical function.
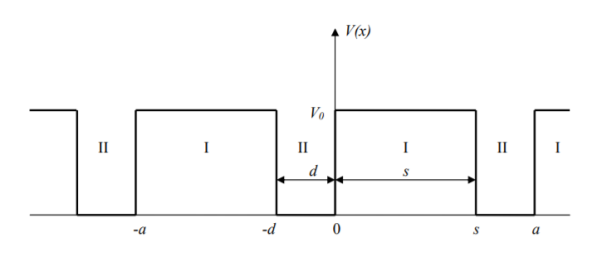
Figure: Potential for the electron in the Kronig-Penney model.
The regions denoted II correspond to the positively charged ions of the crystal lattice. The regions denoted I represent the empty spaces between the ions. It is the choice of this oversimplified potential that makes an analytical solution possible. The lattice parameter is a = d + s. The KP potential is defined by three parameters, e.g., V0, a, and d. The choice of zero on the energy axis has
No influence on the physics of the problem. The single-electron problem is described by the Schrödinger equation.
The single-electron problem is described by the Schrödinger equation.
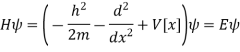
Above can be given separately for regions I and II:
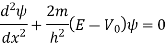
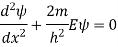
The general solutions are
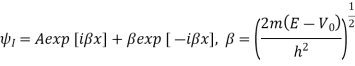
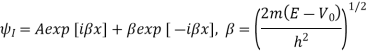
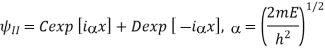
The coefficients A, B, C, D are complex constants determined by the boundary conditions and the normalizing
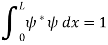
The boundary conditions are that both ψ and dψ d x are continuous functions of x:
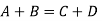
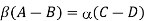
Further relations between the coefficient can be obtained from Bloch’s theorem. Each stationary solution of the Schrödinger equation for a periodical potential can be written in the form
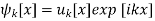
Where uk[x] has the same periodicity as the potential. From equation (6), it also follows that
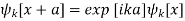
Which means that a translation by a only results in a phase shift of exp[ika]. The same translation symmetry is valid for the derivative of the wave function. By considering the wave function at the points -d and s, we obtain
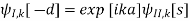
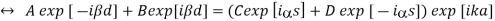
And from the derivatives at -d and s, we have
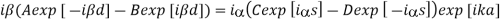
s. In order to obtain nontrivial solutions, the system determinant must vanish. This condition leads to the final equation
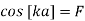
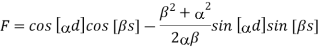
Above equation relates energies E and indices k of possible Bloch functions. E is contained in the equation via α and β. Equation (10) only has real solutions for k in certain energy intervals, when F < 1. These solutions correspond to wavelike solutions. For F > 1, there are no Bloch electrons. The corresponding energy intervals are denoted energy or band gaps.
Energy in Brilloun Zone representation.
We learned about energy bands 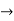 E or
E or 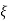 values for which
values for which 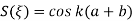 has a solution and between these bands where it is not possible to find a value of E or
has a solution and between these bands where it is not possible to find a value of E or 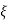 are called forbidden gaps. Discrete number of such bands are separated by band gaps.
are called forbidden gaps. Discrete number of such bands are separated by band gaps.
Now for 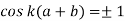
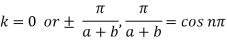
 for these band edges
for these band edges
If we plot the allowed values of energy as a function of k, we obtain the E-k diagram for the one dimensional lattice.
Brillouin zone
When we plot the expanded E-k diagram of Periodic potential perturbation we notice the dissimilarity with the free space E-K diagram (given by the dotted line),
Free Particle Solution
How in particular can the periodic potential solution with an adjustable k approach the free particle solution with a fixed k in the limit where E > >U 0 ?
In this regard it must be remembered that the wave function for an electron in a crystal is the product of two 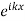 and Q(x) where Q(x) is the wave function in the unit cell. Q(x) is also a function of k. Increasing or decreasing k by
and Q(x) where Q(x) is the wave function in the unit cell. Q(x) is also a function of k. Increasing or decreasing k by 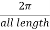 modifies both
modifies both 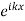 and Q(x) in such a way that the product of
and Q(x) in such a way that the product of 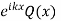 approach the free particle.
approach the free particle.
The k-value associated with given energy band is called a Brillouin Zone.
1 st Brillouin Zone 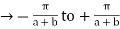
2 nd Brillouin Zone 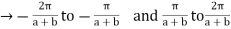
One way of drawing is to k between 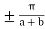 in basically
in basically 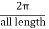 range. In the eigenvalue equation you notice that increasing or decreasing
range. In the eigenvalue equation you notice that increasing or decreasing 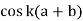 by
by 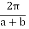 has no effect on the allowed electron energy of E(k) is periodic with a period of
has no effect on the allowed electron energy of E(k) is periodic with a period of 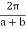 .
.
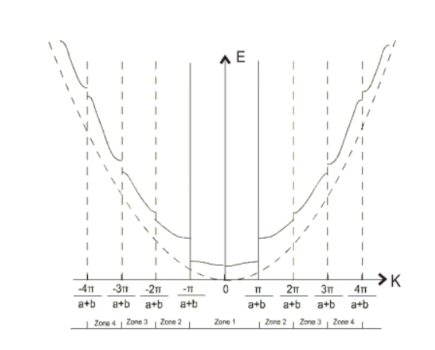
Fig: E k Diagram
Therefore, all the electron energies can be represented within 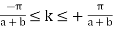 , by changing the k values by
, by changing the k values by 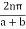 , where n is an integer. This representation of the electron is called the reduced Brillouin zone representation as shown in Fig. 3.9 where the bands of energies are identified. As the number of electrons in the system increases the bands starts to be filled up from the lowest available energies. Normally most of the bands are completely full of electrons as allowed by Pauli's Exclusion Principle. At low temperature, there could be a band completely empty. The one below it is usually completely full, called the valence band. None of these electrons can now conduct electricity. If now a condition arises that some of the electrons from the completely filled band can be excited into the completely empty band, then current can be conducted by the electrons in the empty band called the conduction band.
, where n is an integer. This representation of the electron is called the reduced Brillouin zone representation as shown in Fig. 3.9 where the bands of energies are identified. As the number of electrons in the system increases the bands starts to be filled up from the lowest available energies. Normally most of the bands are completely full of electrons as allowed by Pauli's Exclusion Principle. At low temperature, there could be a band completely empty. The one below it is usually completely full, called the valence band. None of these electrons can now conduct electricity. If now a condition arises that some of the electrons from the completely filled band can be excited into the completely empty band, then current can be conducted by the electrons in the empty band called the conduction band.
Also, according to the Bloch theorem there are two and only two k values associated with each allowed energy, one for the electron moving in the +ve direction and the other for the electron moving in the -ve direction.
Also note that 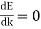 at
at 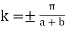 & k = 0. This is a property of all E-k plots.
& k = 0. This is a property of all E-k plots.
References:
1. G. Streetman, and S. K. Banerjee, “Solid State Electronic Devices,” 7th edition, Pearson, 2014.
2. D. Neamen, D. Biswas, "Semiconductor Physics and Devices," McGraw-Hill Education.
3. S. M. Sze and K. N. Kwok, “Physics of Semiconductor Devices,” 3rd edition, John Wiley &Sons, 2006.
4. C.T. Sah, “Fundamentals of Solid State Electronics,” World Scientific Publishing Co. Inc, 1991.
5. Y. Tsividis and M. Colin, “Operation and Modeling of the MOS Transistor,” Oxford univ. Press, 2011.
6. Muhammad H. Rashid, “Electronic Devices and Circuits,” Cengage publication, 2014.