Unit – 2
Network theorems
Superposition theorem states that in any linear, active, bilateral network having more than one source, the response across any element is the sum of the responses obtained from each source considered separately and all other sources are replaced by their internal resistance. The superposition theorem is used to solve the network where two or more sources are present and connected.
If a number of voltage or current sources are acting in a linear network, the resulting current in any branch is the algebraic sum of all the currents that would be produced in it when each source acts alone while all the other independent sources are replaced by their internal resistances.
Example:
The circuit diagram is shown below consists of two voltage sources V1 and V2.
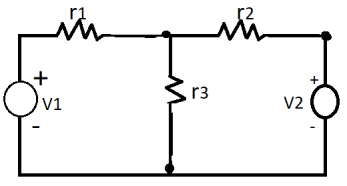
First, take the source V1 alone and short circuit the V2 source as shown in the diagram below:
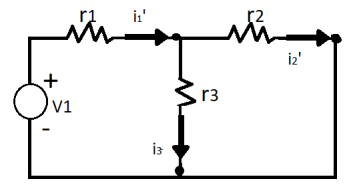
The value of current flowing in each branch, that is i1’, i2’ and i3’ is calculated by the following equations.
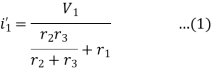
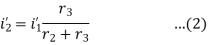
The difference between the two equations gives the value of the current i3’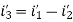
Next, activate the voltage source V2 and deactivating the voltage source V1 by short-circuiting it, find the various currents, that is i1’’, i2’’, i3’’ flowing in the circuit diagram shown below:
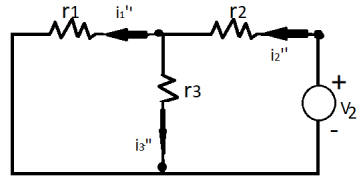
Here,
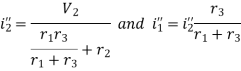
And the value of the current i3’’ will be calculated by the equation shown below: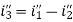
As per the superposition theorem, the value of current i1, i2, i3 is now calculated as:
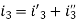
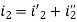
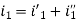
The direction of the current should be taken care of while finding the current in the various branches.
The steps for solving Superposition Theorem
Considering the circuit diagram A, let us see the various steps to solve the superposition theorem:
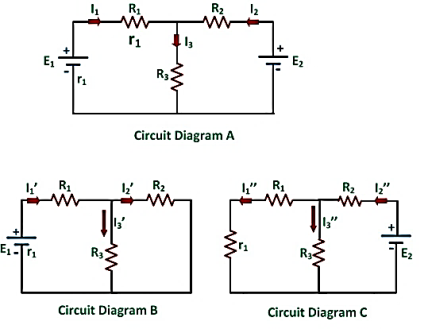
Step 1 – Take only one independent source of voltage or current and deactivate the other sources.
Step 2 – In the circuit diagram B, consider source E1 and replace the other source E2 by its internal resistance. If its internal resistance is not given, then it is taken as zero and the source is short-circuited.
Step 3 – If there is a voltage source than short circuit it and if there is a current source then just open circuit it.
Step 4 – Thus, by activating one source and deactivating the other source find the current in each branch of the network. Taking the above example find the current I1’, I2’and I3’.
Step 5 – Now consider the other source E2 and replace the source E1 by its internal resistance r1 as shown in the circuit diagram C.
Step 6 – Determine the current in various sections, I1’’, I2’’ and I3’’.
Step 7 – Now to determine the net branch current utilizing the superposition theorem, add the currents obtained from each individual source for each branch.
Step 8 – If the current obtained by each branch is in the same direction then add them and if it is in the opposite direction, subtract them to obtain the net current in each branch.
The actual flow of current in the circuit C will be given by the equations shown below:
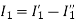
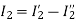
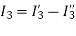 Problem:
Problem:
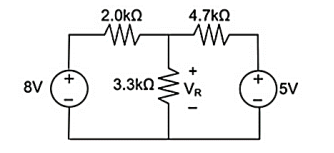
Using Superposition theorem determine the voltage drop and current across the resistor 3.3K as shown in figure below
Step 1:
Remove 8V power supply from the original circuit such that the new circuit becomes as the following and measure the voltage across resistor.
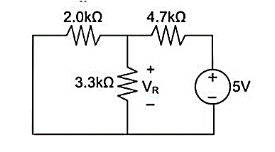
Here 3.3 K and 2K are in parallel therefore the resultant resistance will be 1.245K
Using voltage divider rule across 1.245K will be
V1 =[1.245/(1.245+4.7)] * 5 = 1.047V
Step 2:
Remove the 5V power supply from the original circuit such that the new circuit becomes the following and then measure the voltage across resistor.
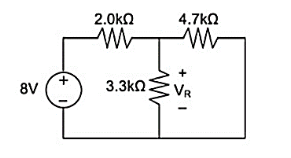
Here 3.3K and 4.7K are in parallel therefore the resultant resistance will be 1.938K. Using voltage divider rule voltage across 1.938K will be
V2 =[1.938(1.938+2)] *8 = 3.9377V
Therefore, voltage drop across 3.3K resistor is V1+V2 = 1.047 + 3.9377 = 4.9847V
Key takeaway
The superposition theorem is used to solve the network where two or more sources are present and connected.
The reciprocity theorem states that in a linear passive bilateral network by changing the voltage source from branch 1 to branch2, the current I in the branch 2 appears in branch 1.
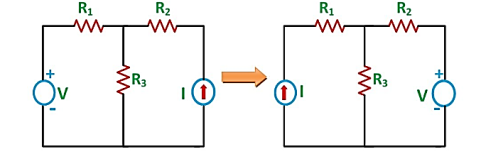
The resistances R1, R2 and R3 is connected in the circuit diagram. It is clearly shown the voltage and current sources are interchanged for solving the network.
Step 1 – Firstly, select the branches between which reciprocity is established.
Step 2 – The current in the branch is obtained using any conventional network analysis method.
Step 3 – The voltage source is interchanged between the branch which is selected.
Step 4 – The current in the branch where the voltage source was existing earlier is calculated.
Step 5 – Hence it is seen that the current obtained in the previous connection, that is step 2 and the current which is calculated when the source is interchanged, that is step 4 are identical to each other.
Problem:
Verify the reciprocity theorem for the given network.
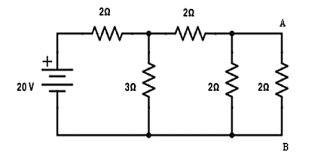
Find the current in branch AB
RT = 2+[3||(2 + 2 || 2)
RT = 3.5 Ω
IT = V / RT = 20/3.5 = 5.71 A
Apply current division technique for the circuit to find the current through branch AB
= 5.71 x 3 / 6 = 2.855 A
Current in branch AB = 2.855 x 2/4 = 1.43A
Interchanging the source to branch AB
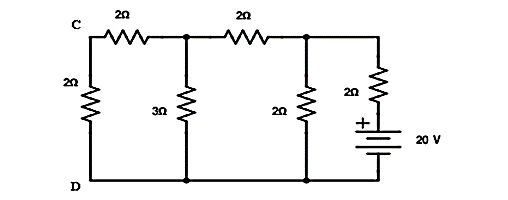
Total resistance RT = 3.23Ω IT = 20/3.23 = 6.19A
Apply current division technique for the circuit to find current through branch CD = 6.19 x 2/5.2 = 2.38A
Current in branch CD = 2.38 x 3/5 = 1.43A
Hence reciprocity theorem verified.
Verify the reciprocity theorem for the given circuit:
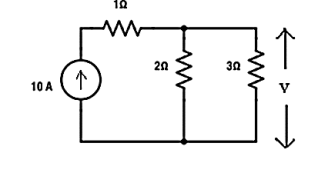
Apply current division technique for the circuit to find current through branch 3Ω
= 10 x 2 / 5 = 4 A.
Voltage across 3Ω = 4 x 3 = 12 V
Replace the current source and find the open circuit voltage.
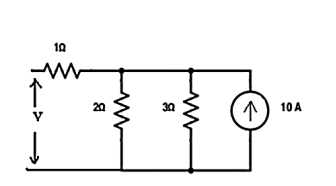
Apply current division technique and find the current through 2 Ω resistor.
= 10 x 3 / 5 = 6
Voltage across 2Ω resistor = voltage across AB = 6 x 2 = 12 V
Key takeaway
The reciprocity theorem states that in a linear passive bilateral network by changing the voltage source from branch 1 to branch2, the current I in the branch 2 appears in branch 1.
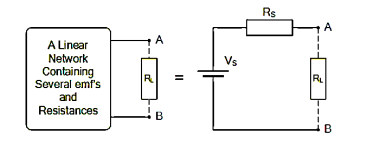
Thevenin’s Theorem states that “Any linear circuit containing several voltages and resistances can be replaced by just one single voltage in series with a single resistance connected across the load”.
To simplify any electrical circuit, to an equivalent two-terminal circuit with just a single constant voltage source in series with a resistance (or impedance) connected to a load as shown below.
Consider the circuit as shown in figure:
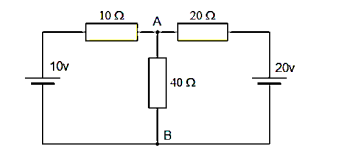
In order to analyse the circuit initially remove the 40Ω load resistor connected across the terminals AB and remove any internal resistance associated with the voltage source.
This is done by shorting out all the voltage sources connected to the circuit. Therefore v=0 or open circuit any connected current sources making i=0.
This because we want to make an ideal voltage source or ideal current source making for circuit analysis.
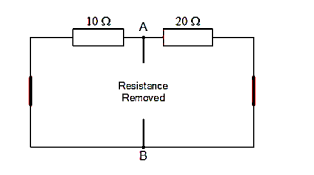
The value of the equivalent resistance, Rs is found by calculating the total resistance looking back from the terminals A and B with all the voltage sources shorted.
10 Ω resistor in parallel with 20Ω resistor
RT = R1 x R2/ R1 + R2 = 20 x 10 / 20 + 10 = 6.67 Ω
Find the equivalent voltage
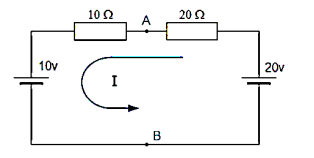
To reconnect the two voltages back into the circuit Vs=VAB the current flowing around the loop is calculated as:
I = V/R = 20 V – 10V / 20 Ω + 10 Ω = 0.33 Amps.
The current is common to both resistors so the voltage drop across the 20Ω resistor or the 10Ω resistor is calculated as:
VAB = 20 –( 20 Ω x 0.33 amps) = 13.33 volts
VAB = 10 + (10 Ω x 0.33 amps) = 13.33 volts
The Thevenin’s Equivalent circuit is a series resistance of 6.67Ω and the voltage source of 13.33 V.
If 40Ω resistor is connected back to the circuit, we get
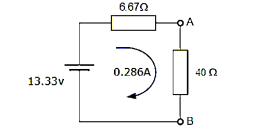
And from this the current flowing around the circuit is given as:
I = V/R = 13.33/6.67 + 40 = 0.286 amps.
Problem:
For the circuit as shown in figure find the current through RL = R2 = 1Ω resistor (Ia-b) branch using Thevenin’s theorem. Find the voltage across the current source.
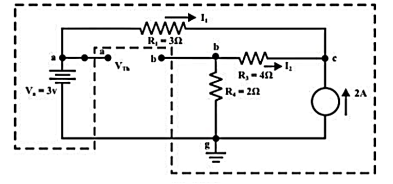
Step 1: Disconnect the load resistance and reconnect the circuit.
Step 2: Apply any method to calculate Vth
At node C
2 + I1 + I2 =0
2 + (3 -Vc)/3 + (0-Vc/6) -- Vc = 6V
The currents I1 and I2 are computed by the following expressions:
I1 = Va -Vc/3 = 3-6/3 = -1A (I1 is flowing from c to a)
I2 = 0 – Vc/6 = -6/6 = -1A (I2 is flowing from c to a)
Step-3:
Redraw the circuit indicating the direction of currents in different branches. One can find the Thevenin’s voltage VTh using KVL around the closed path ‘gabg’
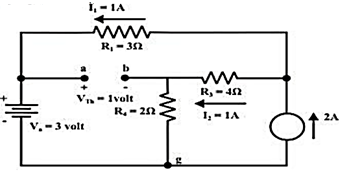
VTh = Vag − Vbg = 3 − 2 =1volt
Step 4:
Replace all sources by their internal resistances. In this problem, voltage source has an internal resistance zero (0) (ideal voltage source) and it is short-circuited with a wire.
On the other hand, the current source has an infinite internal resistance (ideal current source) and it is open-circuited (just remove the current source).
Thevenin’s resistance RTh of the fixed part of the circuit can be computed by looking at the load terminals ‘a’- ‘b’
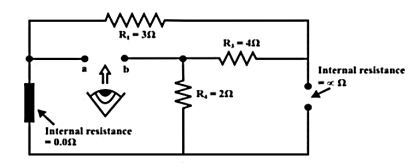
RTh = ( R1 + R3 ) & R4 = ( 3 + 4 )&2 = 1.555Ω
Step-5: Place RTh in series with VTh to form the Thevenin’s equivalent circuit. Reconnect the original load resistance RL = R2 = 1 Ω to the Thevenin’s equivalent circuit.
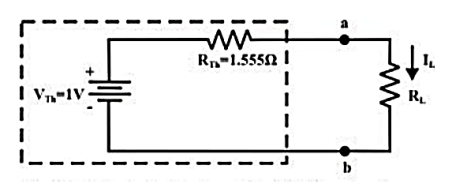
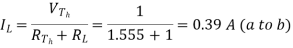
Step-6: The circuit is redrawn to indicate different branch currents. Referring to one can calculate the voltage Vbg and voltage across the current source (Vcg ) using the following equations.
Vbg = Vag − Vab = 3 − 1 × 0.39 =2.61 volt.
Ibg = 2.61 2 = 1.305 A;
Icb = 1.305 − 0.39 = 0.915 A
Vcg = 4 × 0.915 + 2 ×1.305 =6.27 volt.
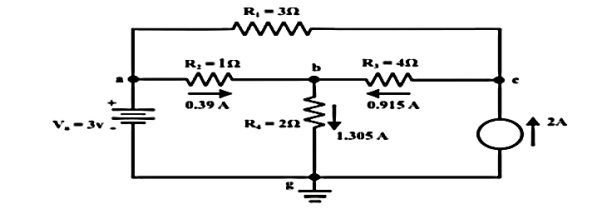
For the circuit shown in figure, find the current IL through 6 Ω resistor using Thevenin’s theorem.
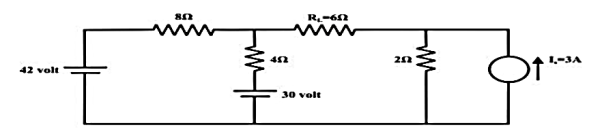
Step-1:
Disconnect 6 Ω from the terminals ‘a’ and ‘b’ and the corresponding circuit diagram. Consider point ‘g’ as ground potential and other voltages are measured with respect to this point.
Step-2:
Apply any suitable method to find the Thevenin’s voltage (VTh)
KVL is applied around the closed path ‘gcag’ to compute Thevenin’s voltage.
42 – 8I – 4I -30 = 0; I = 1A
Vag = 30+4 = 34 volt
Vbg = 2 x 3 = 6 volt
Vth = Vab = Vag – Vbg = 34 -6 = 28 volt
Step-3:
Thevenin’s resistance RTh can be found by replacing all sources by their internal resistances all voltage sources are short-circuited and current sources are just removed or open circuited.
Rth = (8 x4) / 12 + 2 = 14/3 = 4.666Ω
Step-4:
Thevenin’s equivalent circuit is now equivalently represents the original circuit
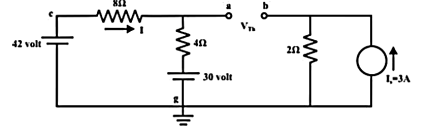
IL = Vth / Rth + RL = 28 / 4.666 +6 = 2.625 A
Norton’s Theorem states that “Any linear circuit containing several energy sources and resistances can be replaced by a single Constant Current generator in parallel with a Single Resistor”.
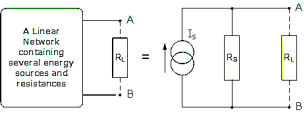
To find the Norton’s equivalent remove the centre 40Ω load resistor and short out the terminals A and B to give us the following circuit.
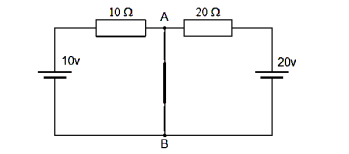
When the terminals A and B are shorted together the two resistors are connected in parallel across their two respective voltage sources and the currents flowing through each resistor as well as the total short circuit current can now be calculated as:
With A-B shorted out
I1 = 10 / 10 = 1A I2 = 20/20 = 1A, Therefore I short-circuit = I1 + I2 = 2 amps
If we short-out the two voltage sources and open circuit terminals A and B, the two resistors are connected in parallel. The value of the internal resistor Rs is found by calculating the total resistance at the terminals A and B giving us the following circuit.
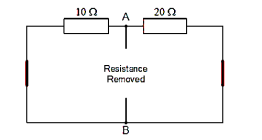
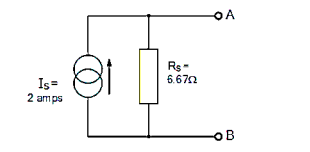
The equivalent resistance is given by 10Ω resistor in parallel with 20 Ω resistor
RT = R1 x R2 / R1 + R2 = 20 x 10 / 20 + 10 = 6.67 Ω.
Norton’s equivalent circuit.
To solve with the original 40Ω load resistor connected across terminals A and B as shown below.
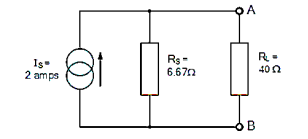
The two resistors are connected in parallel across the terminals A and B which gives us a total resistance of:
RT = R1 x R2 / R1 + R2 = 6.67 x 40 / 6.67 + 40 = 5.72 Ω.
The voltage across the terminals A and B with the load resistor connected is given as:
Va-b = I x R = 2 x 5.72 = 11.44V
Then the current flowing in the 40 Ω load resistor can be found as:
I = V / R = 11.44 / 40 = 0.286 amps.
Problem:
Find RN, IN, the current flowing through and load Voltage across the load resistor in fig (1) by using Norton’s Theorem.
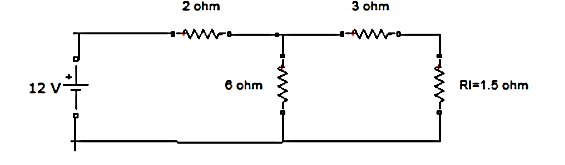
Step 1:
Short the 1.5 Ω load resistor.
Step 2:
Norton current.
Short AB terminals to obtain IN . The total resistance of the circuit is
2Ω + (6Ω || 3Ω)
RT = 4 Ω
IT = V / RT = 12/ 4 = 3 A
IN = 3 A x [ 6Ω / 3 + 6 )] = 2A
IN = 2A
Step 3:
Open current sources, Short Voltage sources and Open Load resistor.
Step 4:
Calculate Norton Resistance (RN)
Reduce 12V dc source. 3Ω resistor is in series with combination of 6Ω and 2Ω resistor
3Ω + (6Ω||2Ω)
3Ω + 1.5 Ω = 4.5 Ω; RN = 4.5 Ω
Step 5:
Connect RN in parallel with current source IN and the load resistor.
Step 6:
The load current through Load resistor
IL = IN x [ RN /(RN + RL)
=2 A x ( 4.5 / 4.5 + 1.5 K) = 1.5 A
IL = 1.5 A
The voltage across load resistor
VL = IL x RL
= 1.5 x 1.5
VL = 2.25 V
Key takeaway
Any linear circuit containing several energy sources and resistances can be replaced by a single Constant Current generator in parallel with a Single Resistor”.
Maximum power transfer theorem states that AC voltage source will deliver maximum power to the variable complex load only when the load impedance is equal to the complex conjugate of source impedance.
Proof:
Replace any two terminal linear network or circuit to the left side of variable load resistor having resistance of RL ohms with a Thevenin’s equivalent circuit. We know that Thevenin’s equivalent circuit resembles a practical voltage source.
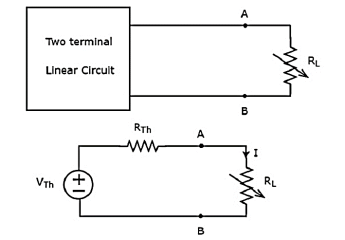
The amount of power dissipated across the load resistor is
PL = I 2 R L ----------------------(1)
Substitute I = Vth / Rth + RL
PL = Vth / (Rth + RL ) 2 RL
PL = Vth 2 { RL / (RTH + RL) 2 ------------------------------(2)
Condition for Maximum Power Transfer
For maximum or minimum, first derivative will be zero. So, differentiate Equation 1 with respect to RL and make it equal to zero.
DPL / d RL = V Th 2 {(Rth + RL) 2 x 1 -RL x 2(Rth + RL) / (Rth + RL) 4} =0
(Rth + RL) 2 – 2RL (Rth + RL) = 0
(Rth + RL) (Rth + RL – 2 RL) = 0
Rth - RL = 0
Rth = RL or RL = Rth
Therefore, the condition for maximum power dissipation across the load is RL=RTh. That means, if the value of load resistance is equal to the value of source resistance that is Thevenin’s resistance, then the power dissipated across the load will be of maximum value.
Substitute RL = Rth and PL = PL,max
PL,max = V th 2 { Rth / (Rth + Rth ) 2 }
= V th 2 ( Rth / 4 Rth 2 )
= V th 2 / 4 Rth
PL,max = V th 2 / 4 RL [RL = Rth]
Efficiency of Maximum power transfer
 = PL,max/ Ps
= PL,max/ Ps
PL,max = maximum amount of power transferred to the load
Ps = amount of power generated by the source.
The amount of power generated by the source is
Ps = I2 Rth + I2 RL
Ps = 2 I2 Rth ; since RL = Rth
Substitute I = Vth / 2 Rth
Ps = 2(Vth / 2Rth) 2 Rth
Ps = 2(Vth / 4Rth) 2 Rth
Ps = Vth 2 / 2 Rth
Substituting with PL max and Ps
= (Vth 2 / 4 Rth) / (Vth 2 / 2 Rth)
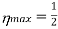
Problem:
Find the maximum power that can be delivered to the load resistor RL of the circuit shown in the following figure.
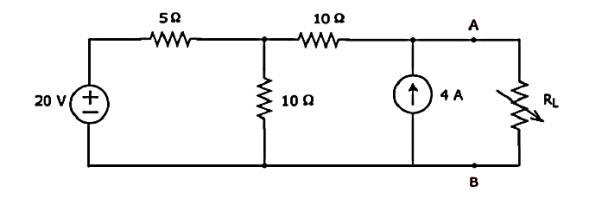
Step 1 – Using Thevenin’s circuit we get
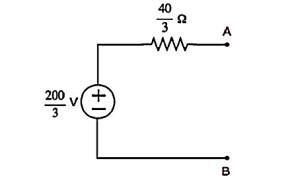
Thevenin’s voltage Vth = 200/3 and Thevenin’s resistance Rth = 40/3
Step 2 – Replace the left side of terminals A & B of the given circuit with the above Thevenin’s equivalent circuit. The resultant circuit diagram will be
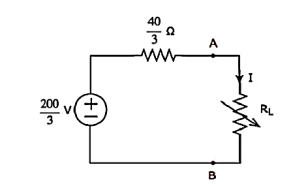
Step 3 − We can find the maximum power that will be delivered to the load resistor, RL by using the following formula.
P L,max = Vth 2 / 4 Rth
Substitute VTh=200/3 and RTh=40/3Ω
P L,max = (200/3) 2 / 4 (40/3)
Therefore, the maximum power that will be delivered to the load resistor RL of the given circuit is 250/3.
Problem:
For the circuit shown find the value of RL that absorbs maximum power from the circuit and the corresponding power under this condition.
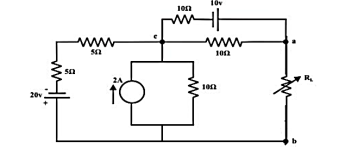
Load resistance RL is disconnected from the terminals ‘a’ and ‘b’ and the corresponding circuit diagram.
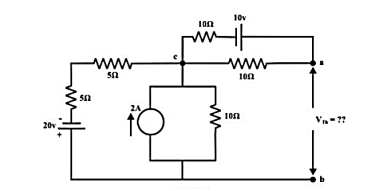
The above circuit is equivalently represented by a Thevenin circuit and the corresponding Thevenin voltage VTh and Thevenin resistance RTh are calculated by following the steps given below:
Considering 20V only
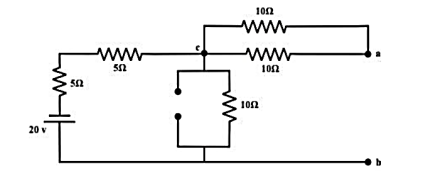
From the above circuit the current through ‘b-c’ branch =20/ 20 = 1𝐴 (𝑓𝑟𝑜𝑚 𝑎 𝑡𝑜 𝑏). Whereas the voltage across the ‘b-a’ branch vba =1 ×10 =10 volt . Since ’b’ is higher potential than ‘a’ ∴vab = − 10volt.
Considering only 10v source only
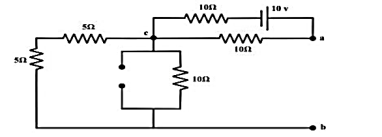
No current is flowing through ‘cb’-branch. Vab = 5v (‘a’ is higher potential than ‘b’). Consider only 2 A current source only
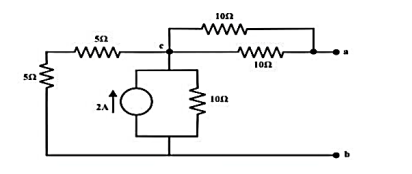
To compute Rth
Replace all voltage and current sources by their internal resistance of the circuit.
Rth = Rab = ((5+5)||10) + (10||10) = 5+5 =10Ω
RL = Rth = 10Ω
The maximum power dissipated to RL is
Pmax = Vth 2 / 4 Rth = ¼ 25 /10 = 0.625 watts
Compensation Theorem
This theorem states that in a linear time-invariant network when the resistance R of an uncoupled branch carrying current I is changed by ∆R then the currents would change which can be obtained by assuming that an ideal voltage source VC has been connected such that Vc = I ∆R in series with (R + ∆R) when all other sources in the network are replaced by their internal resistances.
Let us assume a load RL be connected to a DC source network whose Thevenin’s equivalent gives V0 as the Thevenin’s voltage and RTH as the Thevenin’s resistance as shown in the figure below:
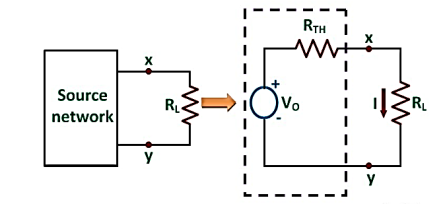
Here,
I = Vo / Rth + RL ------------------------------------(1)
Let the load resistance RL be changed to (RL + ΔRL).
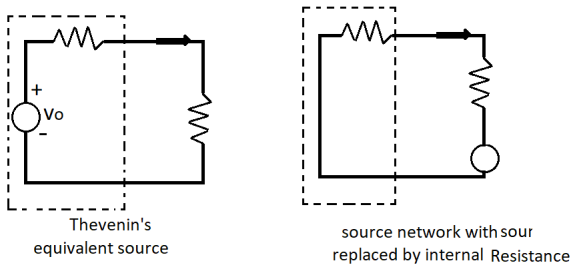
Here,
I ‘ = Vo/ Rth + (RL + ∆ RL) ------------------------(2)
The change of current is ∆I
Therefore,
∆I = I’ – I -------------------------------------(3)
Putting the value of I’ and I from the equation (1) and (2) in equation(3) we get
∆I = Vo / Rth + (RL + ∆ RL) - Vo / Rth + RL --------------------------(4)
∆I = Vo {Rth +RL – (Rth + RL + ∆ RL )} / (Rth + RL + ∆RL ) (Rth + RL)
∆I = - [ Vo/Rth + RL] ∆ RL / Rth + RL + ∆ RL -------------------------------------------------(5)
Now, putting the value of I from the equation (1) in equation (5), we will get the following equation:
∆I = - I ∆ RL / Rth + RL + ∆ RL ------------------------------------------------(6)
VC = I ΔRL and is known as compensating voltage.
∆I = -Vc / Rth + RL + ∆ RL
Hence, Compensation theorem states that the change of branch resistance, results a change in branch currents and the change is equivalent to an ideal compensating voltage source in series with the branch opposing the original current, where all other sources in the network being replaced by their internal resistances.
Problem :
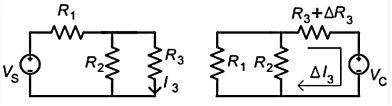
For the circuit as shown in figure. Calculate current I3 . Let the value of resistance change by small value. Calculate the change in current I3.
Vs = 50V, R1 = 4 Ω, R2 = 15 Ω, R3 = 10 Ω, ∆R3 = 5Ω.
I3 = Vs R2/ R1.R2 + R2R3+ R1.R3 = 3A
Vc = (I3 ∆ R3) = 50 V
∆ I3 = -Vc / (R3 + ∆ R3) + R1. R2 / R1 + R2 = -19/23 A
Tallegen's theorem
According to Tallegen theorem, the summation of instantaneous powers for the n number of branches in an electrical network is zero.
Suppose n number of branches in an electrical network have i1, i2, i3, …………. In respective instantaneous currents through them. These currents satisfy Kirchhoff’s Current Law.
Again, suppose these branches have instantaneous voltages across them are v1, v2, v3, ……….. Vn respectively. If these voltages across these elements satisfy Kirchhoff Voltage Law then,
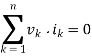
vk is the instantaneous voltage across the kth branch and ik is the instantaneous current flowing through this branch. Tallegen theorem is applicable to lumped networks that consist of linear, non-linear, time variant, time-invariant, and active and passive elements.
Solved Examples
Q1. Find the current through 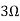 resistance. Using superposition theorem?
resistance. Using superposition theorem?
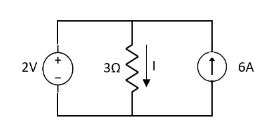
Fig 1 Circuit Diagram
Solution:
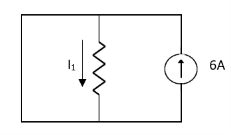
Fig 2 Short circuit 2V
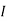 1 = 0
1 = 0
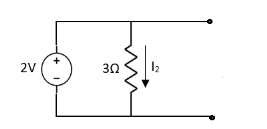
Fig 3 Open circuit 6A
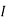 2 =
2 =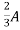
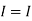 1 +
1 + 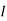 2
2 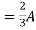
Question 2: Find Value of current I using superposition theorem?
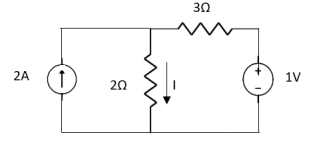
Fig 4 Circuit Diagram
Sol: Applying Superposition Theorem
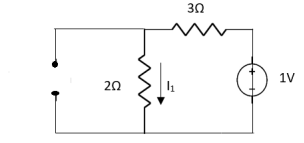
Fig 5 Circuit with 2A open circuit
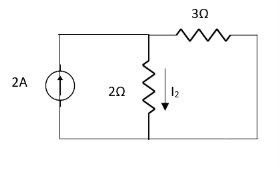
Fig 6 Circuit with 1V short circuit
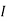 1 =
1 = 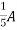
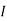 2 =
2 = 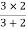
=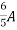
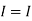 1 +
1 + 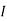 2
2
= 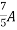
Q3) Find Vth and Rth for the circuit shown below?
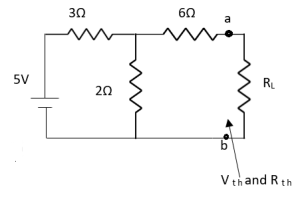
Fig 7 Circuit Diagram
Answer:
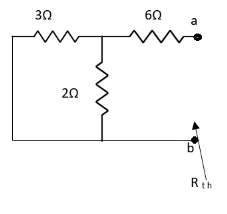
Fig 8 Circuit for finding Rth
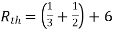
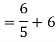
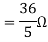
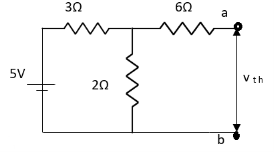
Fig 9 Finding Vth across a and b
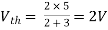
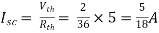
Finding Isc from circuit directly:
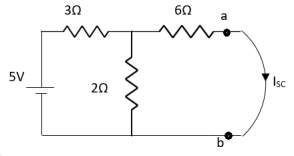
Fig 10 Finding Isc
By KCL,
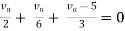
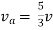
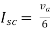
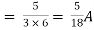
Q4) Find Vth and Rth across a and b?
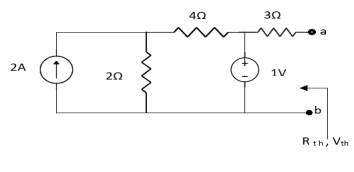
Fig 11 Circuit Diagram
Sol: Finding Rth
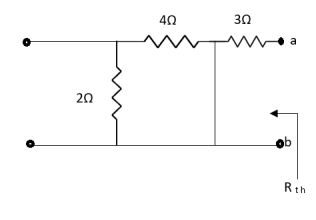
Fig 12 Circuit for Rth
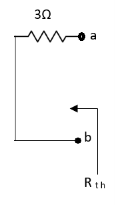
Also, clear from circuit that Vth = 1V.
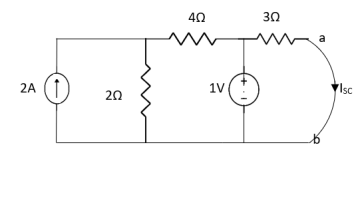
Fig 18 Circuit for Isc
By applying KVL we get,
1-3Isc=0
Isc= A
A
Q5) Find Isc and Rth across terminal a and b?
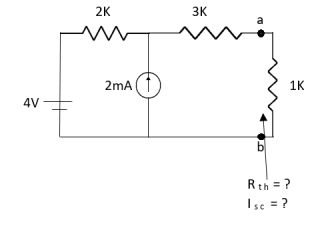
Fig 13 Circuit Diagram
Ans;
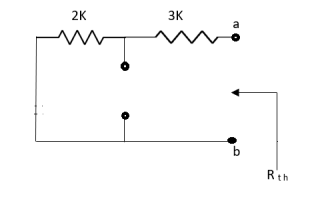
Fig 14 Circuit for finding RTh
Rth=3k+2k=5k
By applying KVL we get
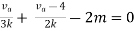
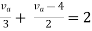
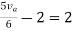
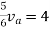
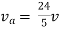
Therefore, 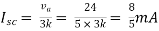
Q6) Find the value of voltage Vx?
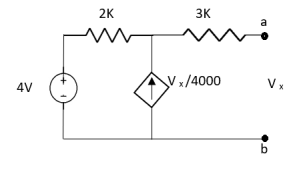
Fig 15 Circuit Diagram
Solution: For Rth
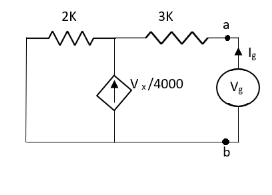
Fig 16 Circuit for finding Rth
By KCL,
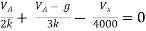
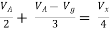
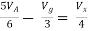
But, 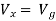
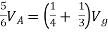
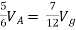
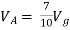
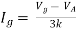
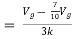
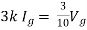
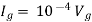
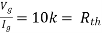
By KVL,
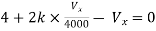
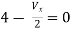
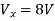
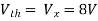
Q7) Find value of current I in the circuit?
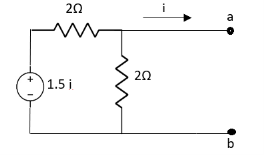
Fig 17 Circuit diagram
Solution: Since, no independent source is present so,
Isc = 0
And we know that,
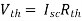
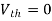
Since Rth cannot be zero
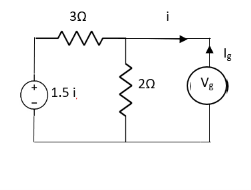
Fig 18 Circuit for finding Rth
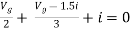
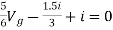
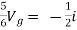
But 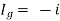
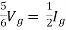
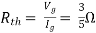
Q8) Find out the Norton’s equivalent
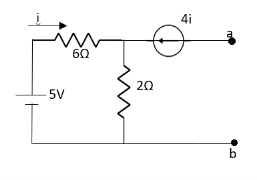
Fig 19 Circuit diagram
Solution:
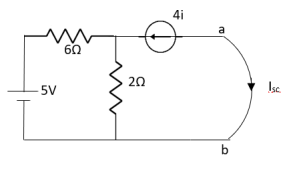
Fig 20 Circuit for finding Isc
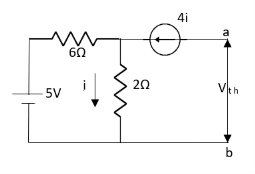
Fig 21 Circuit for finding Vth
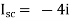
Since, there is no significance of current source
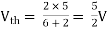
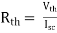
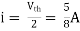
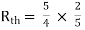
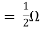
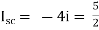 A
A
Q9) Find out the value of load resistance if power absorbed is maximum.
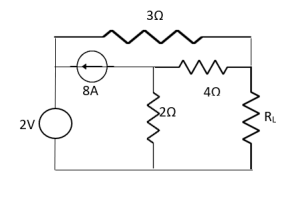
Fig 22 Circuit Diagram
Solution: Find Thevenin’s equation
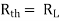
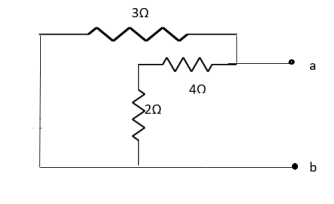
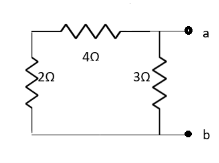
Fig 23 Finding Rth
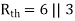
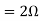
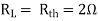
Q10) Find maximum power delivered is RL if its value is
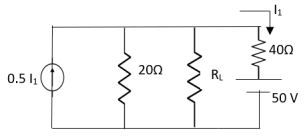
- 16Ω
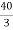 Ω
Ω- 60Ω
- 20Ω
Solution
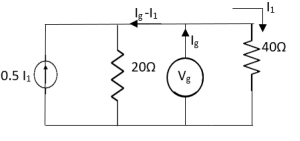
Fig 24 Circuit for finding Rth
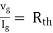
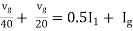
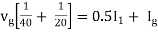
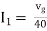
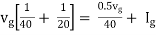
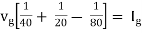
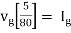
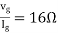
Therefore, 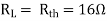
Q11) Verify Reciprocity theorem for given network?
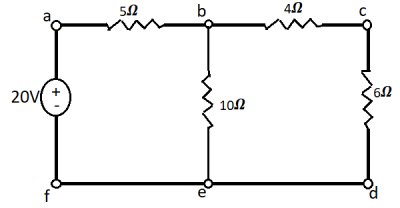
Fig 25 Circuit Diagram
Sol: The value of current Ix flowing due to 20V source is
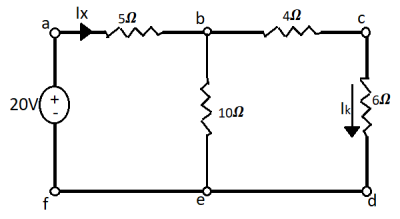
Fig 26 When 20V is at its place
Ix = 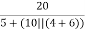 = 2A
= 2A
By current Division
Ik = Ix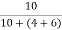 = 1A
= 1A
Now the voltage source of 20V is connected to branch cd. The current by source now will be given as
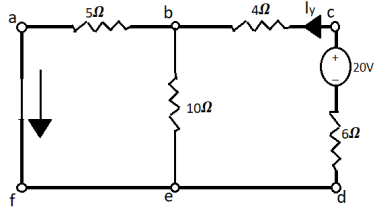
Fig 27 When 20V is connected to cd
Iy= 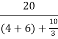 = 3/2 A
= 3/2 A
Then Ij = Iy 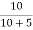 = 1A
= 1A
From above we see that Ik = Ij = 1A
The reciprocity theorem is verified.
References:
1. Franklin F. Kuo, “Network Analysis and Synthesis,” Wiley India Education, 2nd Ed., 2006.
2. Van, Valkenburg, “Network analysis,” Pearson, 2019.
3. Sudhakar, A., Shyammohan, S. P., “Circuits and Network,” Tata McGraw-Hill New Delhi, 1994.
4. A William Hayt, “Engineering Circuit Analysis,” 8th Edition, McGraw-Hill Education.
5. A. Anand Kumar, “Network Analysis and Synthesis,” PHI publication, 2019.