Unit 5
Operational Amplifier
Some of the more common applications are:
- Voltage follower.
- Selective inversion circuit.
- Current to voltage converter.
- Active rectifier.
- Integrator.
- Whole wide variety of filters.
- Voltage comparator.
Key Take-Aways:
Op-amp circuits can be used and designed for applications like amplifiers to filters and integrators to stable and astable multivibrators.
Inverting Amplifier
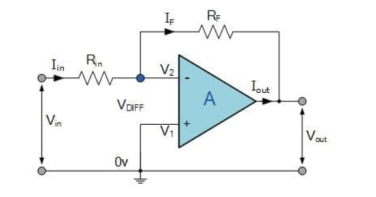
Figure 1. Inverting Amplifier
The input signal vi is applied to the inverting input terminal through resistor R1 and the non-inverting input terminal is grounded. The feedback from the output of the inverting terminal is provided through the feedback resistor Rf.
Since the input is applied to the inverting terminal vo and vi are opposite in polarity and hence the feedback is negative. Since the non-inverting input terminal is grounded v2=0. Due to virtual short at the input of the op-amp, the inverting and non-inverting input terminals are at the same potential.
Therefore, v1 = v2 = 0.
Due to the high input impedance of the Op-amp, the current flowing into its inverting input terminal is zero. Therefore, the same current flows through R1 and Rf.
i 1 = i f
But i1 = vi – v1 / R1 = vi/R1
i f = v1 – vo / Rf = -vo/Rf
Vi/R1 = - vo/Rf
Af = vo/vi = -Rf/R1
Af is the closed loop voltage gain or voltage gain with negative feedback.
Problem :
A 200mV peak to peak sine waveform voltage is applied to Op-amp inverting amplifier with Rf/R1 = 10. Sketch the output.
Solution
Peak to peak input voltage
2Vm = 200 mV
Vm = 100 mV
Vi= Vm sin wt = 100 sin wt mV
Vo = -Rf/R1 x vi = -10 x 100 sinwt mV
= -1000 sin wt mV
Non-inverting amplifier
Non- Inverting amplifier is one in which the output is in phase with respect to input that is if you apply a positive voltage, the output will be positive. The output is a non -inverted amplified version of the input.
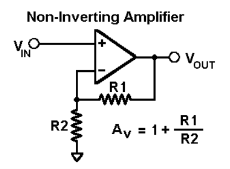
Figure 2. Non-Inverting Amplifier
Assuming the op-amp is ideal and applying the concept of virtual short, the voltage at the inverting terminal is equal to the non-inverting terminal.
Applying KCL at inverting node we get
Vi -Vo/ R2 + Vo – 0 / R1 = 0
By rearranging the terms, we will get
Voltage gain Av = Vo/ Vi = (1+ Rf/Ri)
The gain of non-inverting amplifier Av= (1+ Rf/Ri).
Problem
Design a non-inverting amplifier using Op-amp with a closed-loop voltage gain of 10.
Af = 1 + Rf/R1 =10
Rf/R1 = 9
Rf = 9 R1
If R1 = 1K
Rf = 9K Ω
In an op-amp inverting amplifier R1 = 1K Ω and Rf = 100KΩ. The DC supply voltage of the op-amp is ± 15V. Calculate the output voltage if the input voltage is 1V.
R1 = 1KΩ Rf = 100KΩ
V+ = 15V and V-=-15V. Vi = 1V
Af = -Rf/R1 = -100K/1K = -100
Af = vo/vi
Vo = Af vi
= -100 x 1V = -100V
The output voltage cannot exceed the DC power supply voltage. Since vo is negative and large it is limited to V-
Vo ≈ V- = -15V
Key Take-Aways:
- In the inverting amplifier circuit, the op-amp is connected with feedback to produce a closed-loop operation.
- Non- inverting amplifiers have the same properties as that of inverting except that it has much higher input impedance and does not produce
180 o voltage phase shift.
Integrator:
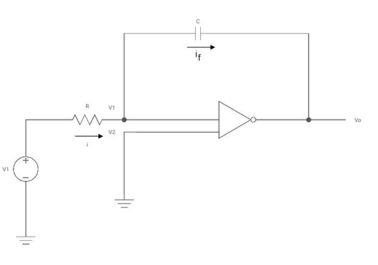
Figure 3. Integrator
Since the non-inverting input terminal of op-amp is grounded v2=0. Due to virtual short at the input of op-amp the inverting and non-inverting input terminals are at the same potential
Therefore v1=v2=0
Due to high impedance of op-amp the current flowing into its input terminal is zero. Therefore the same current flows through R and C
That is
i1 = if -------------------(1)
Where i1 = vi – v1 /R = vi -/R---------------------(2)
And if = C d/dt[v1 – v0] = -C dv0/dt --------------------(3)
Substituting (2) and (3) in (1) we get
Vi = - C/R dv0/dt ------------------------(4)
Dvo/dt = (-1/RC) vi ---------------------------- (5)
Integrating both sides of eq(5) we get
v0 = - 1/RC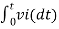 
+ v0(0) --------------------------(6)
Where v0(0) is the initial voltage on the capacitor at t=0.
Note: v0(o) represents the constant of integration.
From eq(6) we find that the output voltage is proportional to the integral of the input voltage.
Therefore v0 = - 1/RC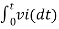 
Problem:
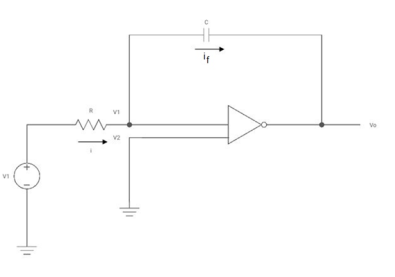
The integrator circuit as shown in the figure has R = 500K Ω and C=1µF. Find and plot the output voltage for the inputs as shown in the figure.
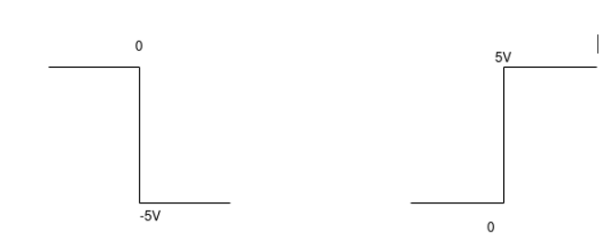
c)vi= 2 sin 4tV d) vi= 4tV
Solution:
We know that
v0 = - 1/RC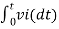 
+ v0(0)
Here R= 500K Ω and C = 1µF
1/RC = 1/ 500 x 1000 x 1 x 10-6
= 1/RC = 2
= -2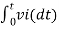 
; vi =- 5V
= -2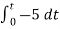 
= 10t V
Which means it is a ramp voltage with a positive slope.
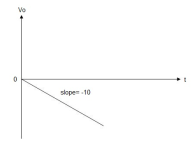
When vi=5V
-2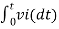 
; vi = 5V
= -2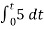 
= -10t V
Which means it is a ramp voltage with a negative slope.
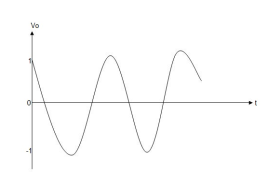
When vi= 2 sin4t V
Vo = -2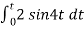 
= -4 [-cos 4t] /4
= cos 4t
When vi=4t V
Vo =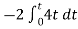 
= -8 [t2/2]
= - 4V
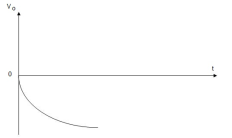
Differentiator
Fig shows an Op-amp differentiator. The circuit of the Op-amp differentiator can be obtained from the Op-amp integrator circuit by simply interchanging the positions of R and C.
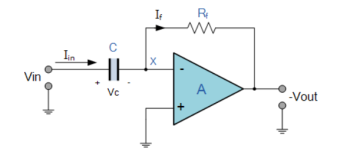
Figure 4. Differentiator
Since the non-inverting and non-inverting input terminals are grounded v2=0. Due to virtual short at the input of Op-amp, the inverting and non-inverting terminals are at the same potential.
v1 = x
v2=0
v1=v2=0
Due to high input impedance of Op-amp, the current flowing into its inverting input terminal in zero. Therefore, same current flows through R and C.
i.e., iin = if ------------------------------------------------------------(1)
But
Iin = C d/dt [ vin – v1] = C dvi/dt ------------------------------------------------(2)
And
If = v1-vo/R = -vo/R ---------------------------------------------------------------------(3)
Using these relations in eq(1) we have
C dvi/dt = -vo/R
Vo = -RC dvi/dt ------------------------------------------------------------------------------(4)
Eq(4) shows that the output voltage vo is proportional to the time derivative of the input.
Key Take-Aways:
- In a differentiator the greater the rate of change of the waveform at the input, the higher the output voltage at that point.
- Op-amp integrator produces the voltage at the output which is proportional to the integral of the input voltage.
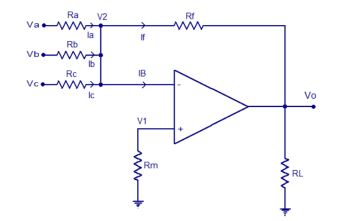
Figure 5. Summing Amplifier
A summing amplifier is a type of operational amplifier circuit that can be used to sum signals. The sum of the input signal is amplified by a certain factor and made available at the output.
Since the non-inverting input terminal of the op-amp is grounded v1=0. Due to virtual short at the input op-amp, the inverting and inverting terminals are at the same potential.
Va=vb=0
i1 = v1-vA/R1 = v1/Ra
i2 = v2 -vA/R2 = v2/Rb
i3 = v3-vA/R3 = v3/Rc
If=vA-vo/Rf = -vo/Rf
Due to the high impedance of op-amp, the current flowing into its inverting input terminal is zero. Apply Kirchhoff’s Current Law at node v2 we have
If = i1+i2+i3
Substituting for i1,i2,i3 and if we have
-vo/Rf = v1/Ra + vb/R2 +vc/R3
Vo = - [ Rf/Ra v1 + Rf/ Rb v2 + Rf/R3 v3]
If we choose Rf =R1=R2=R3 then
Vo = - [ v1+v2+v3]
The output voltage is equal to the negative of the sum of the input voltages. The circuit is called inverting summer due to negative sign.
Key Take-Aways:
- Summing amplifier and its operation
- Summing amplifier applications
Problem:
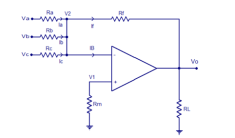
Ra = 10KΩ Va =-1V
Rb = 20KΩ Vb = -2V
Rc= 30kΩ Vc =3V
Rf = 60KΩ
Vo = - [Rf/Ra v1 + Rf/Rb v2 + Rf/Rc v3]
= -[ 60k/10k (-1V) + 60k/20k (-2V) + 60k/30k (3V)]
= -[-6V -6V +6V] = 6V
Calculate the output voltage of a three-input summing amplifier given that
R1 = 200kΩ v1=-2V
R2=250kΩ v2=2V
R3=500kΩ v3=1V
Rf=1MΩ
Vo = -[Rf/R1 v1+ Rf/R2 v2 + Rf/R3 v3]
= - [ 10 6 / 200 x 10 3 Ω (-2V) + 10 6 Ω / 250 x 10 3 (2V) + 10 6 Ω / 500 x 10 3 Ω (1V)]
= -[-10V +8V+2V]
=0V
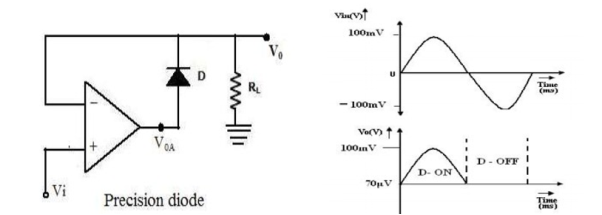
Figure 6. Precision diode and its waveform
A circuit that can act as an ideal diode or precision signal – processing rectifier circuit for rectifying voltages that are below the level of cut-in voltage of the diode can be designed by placing the diode in the feedback loop of an op-amp.
It is a single diode arrangement and functions as a non-inverting precision half-wave rectifier circuit.
If V1 is the circuit of the figure is positive, the op-amp output VOA also becomes positive. Then the closed-loop condition is achieved for the op-amp and the output voltage V0 = Vi.
When Vi < 0, the voltage V0A becomes negative and the diode is reverse biased. The loop is then broken and the output V0 = 0.
Applications: The precision diodes are used in
· half-wave rectifier,
· Full-wave rectifier,
· peak value detector,
· Clipper and clamper circuits.
Key Take-Aways:
- Precision diode rectifier and its operation.
- Precision diode applications.
It is an electronic circuit that adds hysteresis to the input-output transition threshold with the help of positive feedback. Hysteresis here means it provides two different threshold voltage levels for rising and falling edge.
Essentially, a Schmitt Trigger is a Bi-stable Multivibrator and its output remains in either of the stable states indefinitely. For the output to change from one stable state to another, the input signal must change (or trigger) appropriately.
This Bistable operation of the Schmitt Trigger requires an amplifier with positive feedback (or regenerative feedback) with a loop gin greater than one. Hence, a Schmitt Trigger is also known as Regenerative Comparator.
Inverting Schmitt Trigger Circuit
In Inverting Schmitt Trigger, the input is applied to the inverting terminal of the Op-Amp. In this mode, the output produced is of opposite polarity. This output is applied to the non-inverting terminal to ensure positive feedback.
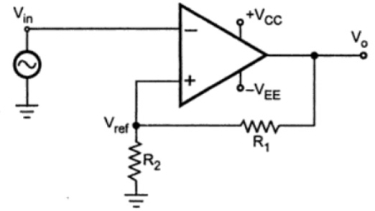
Figure 7. Schmitt trigger
When VIN is slightly greater than VREF, the output becomes -VSAT, and if VIN is slightly less than -VREF (more negative than -VREF), then the output becomes VSAT. Hence, the output voltage VO is either at VSAT or -VSAT, and the input voltage at which these state changes occur can be controlled using R1 and R2.
The values of VREF and -VREF can be formulated as follows:
VREF = (VO x R2) / (R1 + R2), VO = VSAT. Hence, VREF = (VSAT x R2) / (R1 + R2)
-VREF = (VO x R2) / (R1 + R2), VO = -VSAT. Hence, -VREF = (-VSAT x R2) / (R1 + R2)
The reference voltage VREF and -VREF is called Upper Threshold Voltage VUT and Lower Threshold Voltage VLT. The following image shows the output voltage versus input voltage graph also known as the Transfer Characteristic of the Schmitt Trigger.
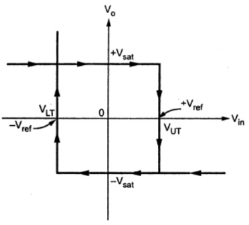
Figure 8. Transfer characteristics of Schmitt trigger
For a pure sinusoidal input signal, the output of an Inverting Schmitt Trigger Circuit is shown in the following image.
Applications:
Schmitt triggers find a wide range of uses mostly as logic inputs.
1.Simple Oscillators
Having two thresholds gives Schmitt triggers the 555 likeabilities to act like predictable oscillators.
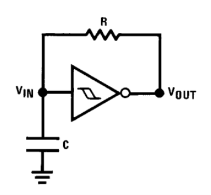
Figure 9. SIMPLE SCHMITT TRIGGER OSCILLATOR
Assume that the capacitor is initially uncharged.
The gate detects this as an input low and sets the output high since it’s an inverting gate. The capacitor begins charging through the resistor R. Once the upper threshold is reached, the gate flips to output low, discharging the capacitor to the low threshold, providing a predictable frequency output.
The expression for frequency can be derived as:
f ≈ 1/ RC ln VT + (VDD -VT-) / VT – (VDD -VT+)
Where R and C are the resistance and capacitance, VT + is the upper threshold, VT – is the lower threshold and VDD is the supply voltage.
2. Switch Debouncing
The switch contacts tend to be somewhat springy which causes a lot of unwanted jitters, which again can cause multiple transitions and glitches further down the line.
Using a Schmitt trigger with a simple RC circuit can help mitigate these problems.
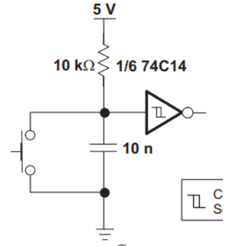
Figure 10. SCHMITT TRIGGER SWITCH DEBOUNCER
When the switch is pressed, it discharges the capacitor and causes the output to go high for a moment till the capacitor charges up again, creating a clean pulse on the output.
Key Take-Aways:
- Schmitt trigger and its operation
- Schmitt trigger applications
Active filter
Active filters are the electronic circuits, which consist of an active element like op-amp(s) along with passive elements like a resistor(s) and capacitor(s).
Active filters are mainly classified into the following four types based on the band of frequencies that they are allowing and/or rejecting −
- Active Low Pass Filter
- Active High Pass Filter
- Active Band Pass Filter
- Active Band Stop Filter
Active Low Pass Filter
If an active filter allows or passes only low-frequency components and rejects or blocks all other high-frequency components, then it is called an active low pass filter.
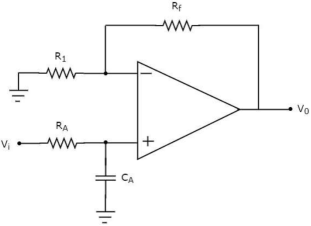
Figure 11. Active Low Pass filter
The electric network, which is connected to the non-inverting terminal of an op-amp is a passive low pass filter. So, the input of a non-inverting terminal of an op-amp is the output of a passive low pass filter.
It produces an output that is (1+Rf/R1) times the input present at the non-inverting terminal.
Active High Pass Filter
If an active filter allows or passes only high-frequency components and rejects or blocks all other low-frequency components, then it is called an active high pass filter.
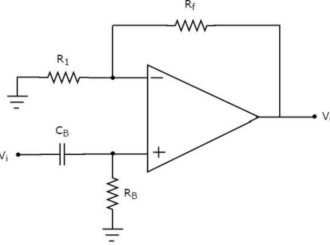
Figure 12. Active high pass filter
So, the input of a non-inverting terminal of the op-amp is the output of a passive high pass filter.
The circuit resembles a non-inverting amplifier having the output of a passive high pass filter as an input to the non-inverting terminal of op-amp. Hence, it produces an output, which is (1+Rf/R1) times the input present at its non-inverting terminal.
Active Band Pass Filter
If an active filter allows only one band of frequencies, then it is called an active bandpass filter. In general, this frequency band lies between the low-frequency range and a high-frequency range. So, the active bandpass filter rejects both low and high-frequency components.
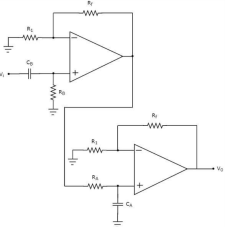
Figure 13. Active Band Pass filter
There are two parts in the circuit diagram of the active bandpass filter: The first part is an active high pass filter, while the second part is an active low pass filter.
The output of the active high pass filter is applied as an input of the active low pass filter. That means both active high pass filter and active low pass filter are cascaded to obtain the output in such a way that it contains only a particular band of frequencies.
Active BandStop filters
If an active filter rejects (blocks) a particular band of frequencies, then it is called an active bandstop filter. In general, this frequency band lies between the low-frequency range and a high-frequency range. So, an active band stop filter allows passes of both low and high-frequency components.
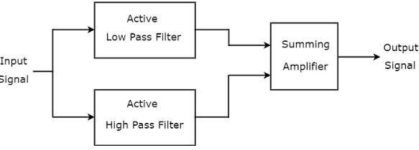
Figure 14. Active Bandstop filters.
The block diagram of an active band stop filter consists of two blocks in its first stage: an active low pass filter and an active high pass filter. The outputs of these two blocks are applied as inputs to the block that is present in the second stage. So, the summing amplifier produces an output, which is then an amplified version of the sum of the outputs of the active low pass filter and the active high pass filter.
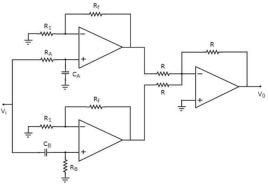
Figure 15. Band Stop filter
Key Take-Aways:
- What is the active filter?
- The types of active filters.
Active low pass filter:
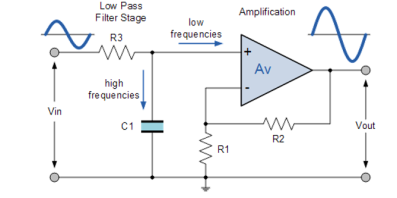
Figure 16. Active low pass
The frequency response of the circuit will be the same as that for the passive RC filter, except that the amplitude of the output is increased by the passband gain, AF of the amplifier.
For a non-inverting amplifier circuit, the magnitude of the voltage gain for the filter is given as a function of the feedback resistor ( R2 ) divided by its corresponding input resistor ( R1 ) value and is given as:
DC gain = (1+R2/R1)
Therefore, the gain of an active low pass filter as a function of frequency will be:
The gain of a first-order low pass filter
Voltage gain (Av) = Vout / Vin = AF/ √ 1+ (f/fc) 2
Where:
- AF = the passband gain of the filter, (1 + R2/R1)
- ƒ = the frequency of the input signal in Hertz, (Hz)
- ƒc = the cut-off frequency in Hertz, (Hz)
Thus, the operation of a low pass active filter can be verified from the frequency gain equation above as:
- At very low frequencies f<fc
Vout/Vin = AF
- 2. At the cut-off frequency, ƒ = ƒc
Vout/Vin = AF/ √2 = 0.707 AF
- 3. At very high frequencies, ƒ > ƒc
Vout/Vin < AF
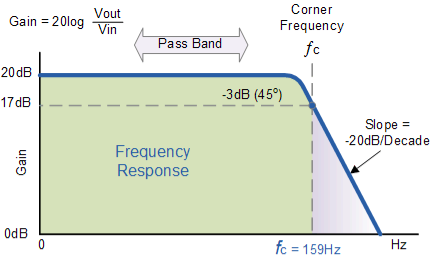
Thus, the Active Low Pass Filter has a constant gain AF from 0Hz to the high-frequency cut-off point, ƒC. At ƒC, the gain is 0.707AF, and after ƒC, it decreases at a constant rate as the frequency increases. That is when the frequency is increased tenfold (one decade), the voltage gain is divided by 10.
When dealing with filter circuits the magnitude of the passband gain of the circuit is generally expressed in decibels or dB as a function of the voltage gain, and this is defined as:
The magnitude of Voltage Gain in (dB)
Av (dB) = 20 log 10 (Vout/Vin)
-3dB = 20 log (0.707 Vout/Vin)
Active Low Pass Filter
Design a non-inverting active low pass filter circuit that has a gain of ten at low frequencies, a high-frequency cut-off or corner frequency of 159Hz, and an input impedance of 10KΩ.
The voltage gain of a non-inverting operational amplifier is given as:
AF = 1+R2/R1 = 10
Assume a value for resistor R1 of 1kΩ rearranging the formula above gives a value for R2 of:
R2 = (10-1) x R1 = 9 x 1KΩ = 9kΩ
So for a voltage gain of 10, R1 = 1kΩ and R2 = 9kΩ. However, a 9kΩ resistor does not exist so the value of 9kΩ is used instead.
Converting this voltage gain to an equivalent decibel dB value gives:
Gain in dB = 20 log A = 20 log 10 = 20dB
The cut-off or corner frequency (ƒc) is given as being 159Hz with an input impedance of 10kΩ. This cut-off frequency can be found by using the formula:
Fc = 1/ 2π RC Hz where fc= 159 Hz and R=10kΩ
By rearranging the above standard formula we can find the value of the filter capacitor C as:
C = 1/ 2π fc R = 1/ 2 π x 159 x 10 kΩ = 100nF
Thus the final low pass filter circuit along with its frequency response is given below as:
Low Pass Filter Circuit
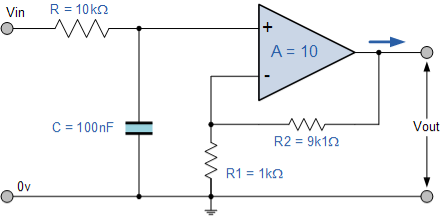
Frequency Response Curve
If the external impedance connected to the input of the filter circuit changes, this impedance change would also affect the corner frequency of the filter. One way of avoiding any external influence is to place the capacitor in parallel with the feedback resistor R2 effectively removing it from the input but still maintaining the characteristics of the filter.
However, the value of the capacitor will change slightly from being 100nF to 110nF to take account of the 9k1Ω resistor, but the formula used to calculate the cut-off corner frequency is the same as that used for the RC passive low pass filter.
Fc = 1/ 2π C R2 Hertz
Design of High Pass filter
The specifications are:
- Gain is 2
- The cut-off frequency is 2KHz
Amplifier gain
Af = 1+R3/R2
Af =2
Let R2 = 1K
By putting these values we get
R3 = 1K
Now we need to calculate the value of the resistor according to the cut-off frequency.
The value of the capacitor if the cut-off frequency is 2KHz, we selected the value of the capacitor is 0.01uF or 10nF.
Fc = 1/ 2πRC
By putting all value together we get R = 8K
To calculate gain
Voltage gain (Af) = Af (f/fc) / √ 1 + (f/fc) 2
Now changing the frequency we get the gain as
Frequency | Voltage gain (Vout/Vin) | Gain = 20 log (Vout/Vin) |
100 | 0.10 | -20.11 |
250 | 0.25 | -12.11 |
500 | 0.49 | -6.28 |
750 | 0.70 | -3.07 |
1000 | 0.89 | -0.97 |
2000 | 1.41 | 3.01 |
5000 | 1.86 | 5.38 |
10,000 | 1.96 | 5.85 |
50,000 | 2 | 6.01 |
1,00,000 | 2 | 6.02 |
In this table from the 100 Hz the gain is sequentially increased at a pace of 20dB/decade but after the cut-off frequency is reached the gain is slowly increased to 6.02dB and remains constant.
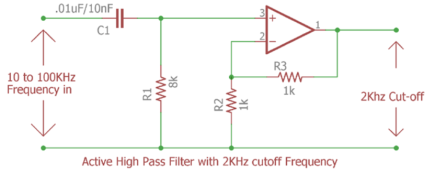
Figure 17. High Pass filter
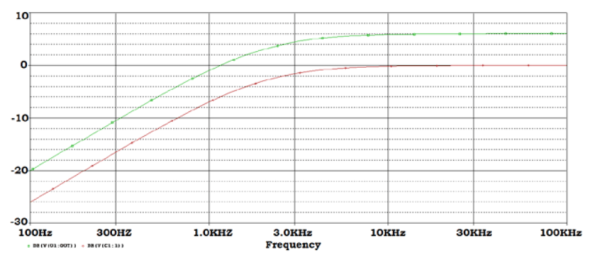
Figure 18. Frequency response
Design of Band Pass filter:
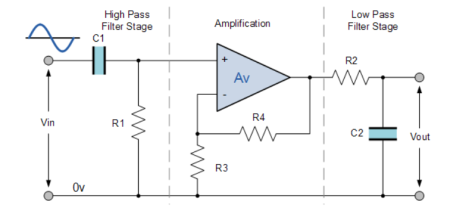
Figure 19. Band Pass filter
The cascading together of the individual low and high pass passive filters produces a low “Q-factor” type filter circuit which has a wide passband. The first stage of the filter will be the high pass stage that uses the capacitor to block any DC biasing from the source.
This design has the advantage of producing a relatively flat asymmetrical passband frequency response with one half representing the low pass response and the other half representing the high pass response as shown.
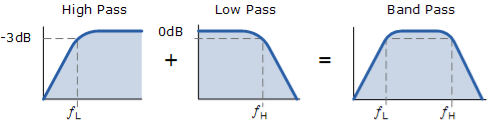
Figure 20. Band Pass Frequency response
The higher corner point ( ƒH ), as well as the lower corner frequency cut-off point ( ƒL ), are calculated the same as before in the standard first-order low and high pass filter circuits.
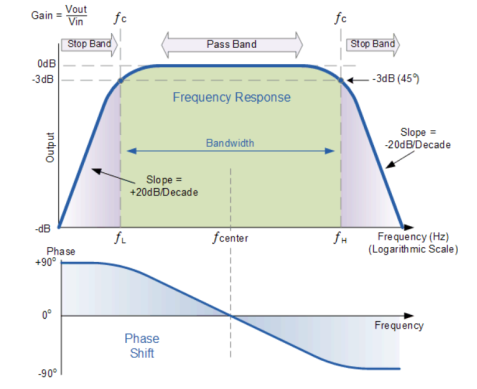
Figure20.Amplitude and Phase response
For an active bandpass filter, the lower cut-off -3dB point is given by ƒC1 while the upper cut-off -3dB point is given by ƒC2.
Inverting Band Pass Filter Circuit
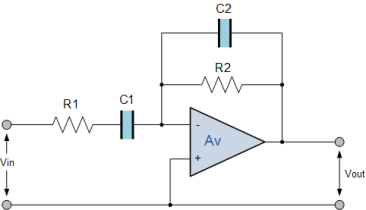
Figure 21.Inverting Band Pass filter
Voltage gain = -R2/R1 fc1 = 1/ 2 π R1 C1 , fc2 = ½ π R2 C2
This type of bandpass filter is designed to have a much narrower passband. The centre frequency and bandwidth of the filter are related to the values of R1, R2, C1 , and C2. The output of the filter is again taken from the output of the op-amp.
An active bandpass filter that has a voltage gain Av of one (1) and a resonant frequency, ƒr of 1kHz is constructed using an infinite gain multiple feedback filter circuit. Calculate the values of the components required to implement the circuit.
Firstly, we can determine the values of the two resistors, R1 and R2 required for the active filter using the gain of the circuit to find Q as follows.
Av =1= -2 Q 2
Q BP = 1/√2 = 0.707
Q = 0.7071 = ½ √ R2/R1
R2/R1 = (0.707/ ½ ) 2 =2
Then we can see that a value of Q = 0.7071 gives a relationship of the resistor, R2 is twice the value of resistor R1. Then we can choose any suitable value of resistances to give the required ratio of two. Then resistor R1 = 10kΩ and R2 = 20kΩ.
The center or resonant frequency is given as 1kHz. Using the new resistor values obtained, we can determine the value of the capacitors required assuming that C = C1 = C2.
Fr = 1000Hz = 1/ 2 π C √ R1 R2
C = 1/ 2π fr √R1 R2 = 1/ 2π 1000 √10,000 x 20,000 = 11.2 nF
The closest standard value is 10nF.
Design of band-stop filter:
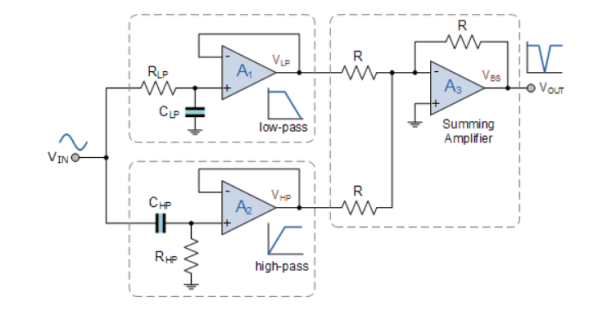
Figure 22. Band Stop filter circuit
The use of operational amplifiers within the bandstop filter design also allows us to introduce voltage gain into the basic filter circuit. The two non-inverting voltage followers can easily be converted into a basic non-inverting amplifier with a gain of Av = 1 + Rƒ/Rin
Design a basic wide-band, RC band stops filter with a lower cut-off frequency of 200Hz and a higher cut-off frequency of 800Hz.
Find the geometric center frequency, -3dB bandwidth, and Q of the circuit.
f= 1/2πRC
The upper and lower cut-off frequency points for a band stop filter can be found using the same formula as that for both the low and high pass filters as shown.
Assuming a capacitor, C value for both filter sections of 0.1uF, the values of the two frequency-determining resistors, RL and RH are calculated as follows.
Low Pass Filter Section
FL = 1/ 2π RL C = 200Hz and C = 0.1 μF
RL = 1/ 2π x 200 x 0.1 x 10 -6 = 7958 or 8KΩ
High Pass Filter Section
FH = 1/2π RH C = 800Hz and C = 0.1 μF
RH = 1/ 2π x 800 x 0.1 x 10 -6 = 2 K Ω
From this we can calculate the geometric center frequency, ƒC as:
Fc = √ fL x fH = √ 200 x 800 = 400Hz
FBW = fH -fL = 800 -200 = 600 Hz
Q = fc/ fBW = 400/600 = 0.67 or -3.5 db
Key Take-Aways:
- Design for all the active filters
References:
- Fundamentals of Analog Circuits (English, Paperback, Floyd Thomas L.)
2. A Text Book on Analog Electronics - EE/E&T/IN by A Rajkumar, Made Easy Publications.
3. Analog Electronics by J.B Gupta
4. Design with Operational Amplifier and Analog Integrated Circuits by Sergio Franco.
