Unit 4
The Z-Transform
Consider applying complex exponential input x(n) = z n to an LTI system with impulse response h(n). The system output is given by
y(n) = h(n) * x(n)
= 
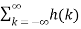x(n-k) = 
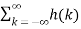z(n-k)
= z n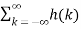 
z-k
= z n H(z).
H(z) is known as the transfer function of LTI system.
We know that a signal for which the system output is a constant times, the input is referred to as an eigen function of the system and the amplitude factor is referred to as the system’s eigen value. Hence, we identify zn as an eigen function of the LTI system and H(z) is referred to as the Bilateral z-transform or simply z-transform of the impulse response h(n).
The transform relationship between x(n) and X(z) is
x(n) -> X(Z)
Key Takeaways:
- Z transform of discrete signal
- Identifying eigen function of LTI system
Region of Convergence of z-Transform
The open region where X(z) converges is referred to as the region of convergence (ROC) of X(z).
The ROC may mean the region where X(z) converges. It should be noted that both the algebraic expression and the ROC of X(z) are required to specify x(n) uniquely.
Assume that x(n) has the z-transform X(z).
For different types of x(n), the ROC of X(z) has different types.
(1) If x(n) is of finite duration, then the ROC of X(z) is the entire plane, i.e., zC. Especially, z=0 needs to be excluded from the ROC if x(n) has nonzero values for n>0.
(2) If x(n) is right-sided, then the ROC of X(z) is the exterior of a circle centered about the origin, i.e., |z|>r0 .
(3) If x(n) is left-sided, then the ROC of X(z) is the interior of a circle centered about the origin, i.e., |z|0. (4) If x(n) is two-sided, then the ROC of X(z) is a ring centered about the origin, i.e., r1<|z|
Key Takeaways:
ROC representation for Z-domain
Its representation for different sides
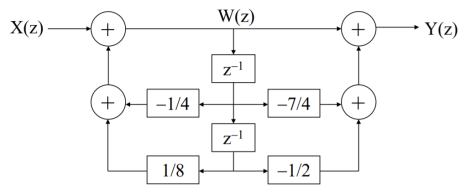
A block diagram consists of three elements, that is, the adder, the coefficient multiplier and the delayer. Figure shows these elements.
Example. Suppose that a causal linear time-invariant discrete-time system is characterized by
H(z)= 1- (7/4 ) z-1 –(1/2) z -2 / 1+(1/4) z-1 – (1/8) z -2
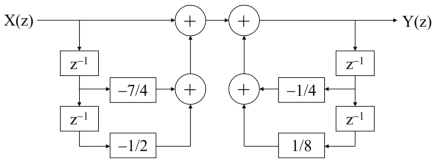
We obtain Y(z)=(1/4)z1Y(z)+(1/8)z2Y(z)+ X(z)(7/4)z1X(z)(1/2)z2X(z).
Y(z) = 1-7/4 z-1 – ½ z-2 / 1+1/4 z-1 -1/8 z-2
Y(z) = [ 1-(7/4) z-1 – (1/2) z-2 ] W(z)
W(z) = 1/ 1+1/4 z-1 -1/8 z-2 X(z)
W(z) = -(1/4) z-1 W(z) +(1/8) z-2 W(z) +X(z)
Y(z) = W(z) – (7/4) z-1 W(z) –(1/2) z-2 W(z)
Key Takeaways:
- Representation of Z domain analysis for different systems
References:
1. A.V. Oppenheim, A.S. Willsky and I.T. Young, "Signals and Systems," Pearson, 2015.
2. R.F. Ziemer, W.H. Tranter and D.R. Fannin, "Signals and Systems - Continuous and Discrete," 4th edition, Prentice Hall, 1998.
3. B.P. Lathi, "Signal Processing and Linear Systems," Oxford University Press, 1998.
4. Douglas K. Lindner, "Introduction to Signals and Systems," McGraw Hill International Edition: 1999.
5. Simon Haykin, Barry van Veen, "Signals and Systems," John Wiley and Sons (Asia) Private Limited, 1998.
6. V. Krishnaveni, A. Rajeswari, “"Signals and Systems," Wiley India Private Limited, 2012.
7. Robert A. Gabel, Richard A. Roberts, "Signals and Linear Systems," John Wiley and Sons, 1995.
8. M. J. Roberts, "Signals and Systems - Analysis using Transform methods and MATLAB," TMH, 2003.
9. J. Nagrath, S. N. Sharan, R. Ranjan, S. Kumar, "Signals and Systems," TMH New Delhi, 2001.
10. A. Anand Kumar, “Signals and Systems,” PHI 3rd edition, 2018.
11. D. Ganesh Rao, K.N. Hari Bhat, K. Anitha Sheela, “Signal, Systems, and Stochastic Processes,” Cengage publication, 2018
