Module 1
Matrices
Definition:
An arrangement of m.n numbers in m rows and n columns is called a matrix of order mxn.
Generally, a matrix is denoted by capital letters. Like, A, B, C, ….. etc.
Upper triangular and lower triangular matrices,
14. Conjugate of a matrix
15. Symmetric matrix
16. Skew – symmetric matrix
Operations on matrices:
Elementary transformations
a) Elementary row transformation
These are three elementary transformations
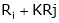
b) Elementary column transformations:
There are three elementary column transformations.
The rank of a matrix:
Let A be a given rectangular matrix of a square matrix. From this matrix select, any r rows from these r rows select any r columns thus getting a square matrix of order r x r. The determinant of this matrix of order r x r is called a minor of order r.
e.g.
If 
For example, select the 2nd and 3rd row. i.e.
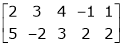
Now select any two columns. Suppose 1st and 2nd.
i.e. 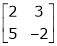
Definition: The number of independent rows in a matrix is called the row rank, the number of independent columns in a matrix is called the column rank.
Theorem: The row rank and column rank of any matrix are the same.
Invariance of rank through elementary transformations.
The rank of A = Rank of B
2. Equivalent matrices:
The matrix B is obtained from a matrix A by a sequence of a finite no. of elementary transformations is said to be equivalent to A. and we write.
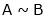
Normal form or canonical form:
Every mxn matrix of rank r can be reduced to the form 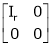
By a finite sequence of elementary transformation. This form is called the normal form or the first canonical form of the matrix A.
Ex. 1
Reduce the following matrix to the normal form of Hence find it’s rank,
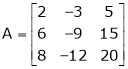
Solution:
We have,
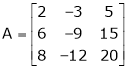
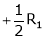
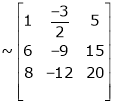
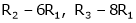
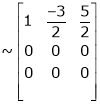
Apply 
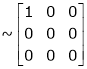
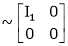
 The rank of A = 1
The rank of A = 1
Ex. 2
Find the rank of the matrix
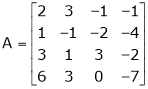
Solution:
We have,
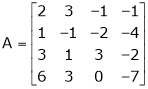
Apply R12

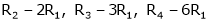

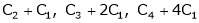

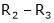

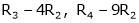

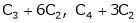

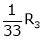
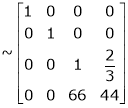
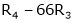

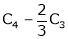


 The rank of A = 3
The rank of A = 3
Ex. 3
Find the rank of the following matrices by reducing it to the normal form.
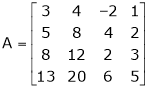
Solution:
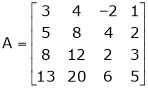
Apply C14

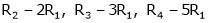

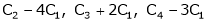

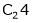

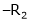

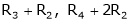

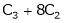


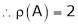
H.W.
Reduce the follo9wing matrices into the normal form and hence find their ranks.
a) 
b) 
2. Reduction of a matrix a to normal form PAQ.
If A is a matrix of rank r, then there exists a non – singular matrices P & Q such that PAQ is in normal form.
i.e. 
To obtain the matrices P and Q we use the following procedure.
Working rule:-
So that A on the l.h.s. reduces to normal form.
Example 1
If  Find Two
Find Two
Matrices P and Q such that PAQ is in normal form.
Solution:
Here A is a square matrix of order 3 x 3. Hence, we write,
A = I3 A.I3
i.e. 
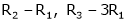
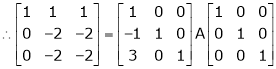


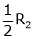
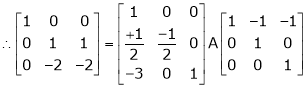
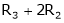
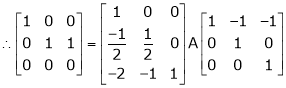
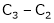
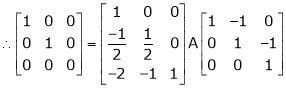
i.e. 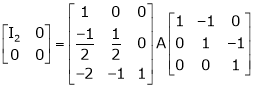
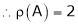
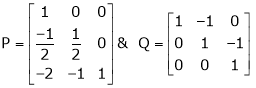
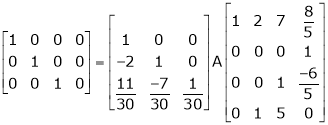
Example 2
Find a non – singular matrices p and Q such that P A Q is in a normal form where
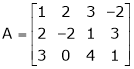
Solution:
Here A is a matrix of order 3 x 4. Hence, we write A as,
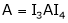
i.e.
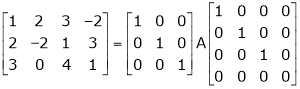
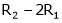
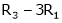
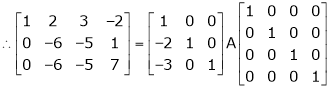
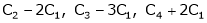
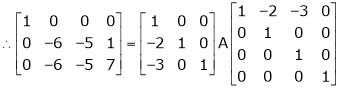

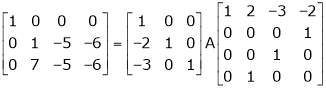
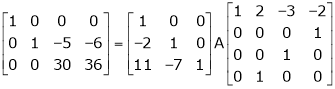
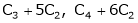
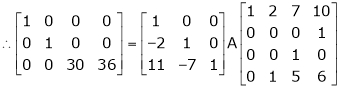
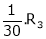
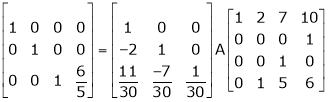
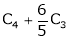
i.e. 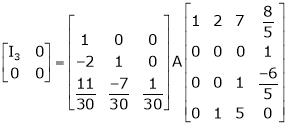

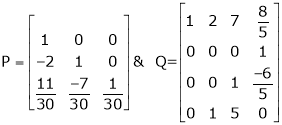
Let A be a square matrix,  be any scaler then
be any scaler then 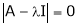 is called a characteristic equation of a matrix A.
is called a characteristic equation of a matrix A.
Note:
Let a be a square matrix and ‘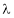 ’ be any scaler then,
’ be any scaler then,
1)  is called a characteristic matrix
is called a characteristic matrix
2) 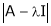 is called a characteristic polynomial.
is called a characteristic polynomial.
The roots of characteristic equations are known as characteristic root or latent roots, eigenvalues, or proper values of a matrix A.
Every square matrix satisfied its characteristic equation
Ex.
Verify Cayley – Hamilton theorem and use it to find A4 and A-1
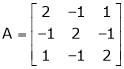
Ex. Verify Cayley – Hamilton theorem and hence find A-1, A-2, A-3
Ex. For 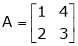 find the value of
find the value of 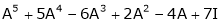 , using Cayley Hamilton theorem.
, using Cayley Hamilton theorem.
Ex. Find the characteristic equation of the matrix
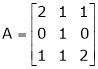
And hence find the matrix represented by
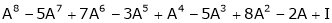
Verify whether the following matrix is orthogonal or not if so find A-1
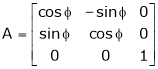
Introduction:
In this chapter we are going to study a very important theorem viz first we have to study eigenvalues and eigenvector.
An ordered n-tuple of numbers is called an n – vector. Thus the ‘n’ numbers x1, x2, ………… xn took in order denotes the vector x. i.e. x = (x1, x2, ……., xn).
Where the numbers x1, x2, ……….., xn are called component or coordinates of a vector x. A vector may be written as a row vector or a column vector.
If A be an mxn matrix then each row will be an n – vector & each column will be an m – vector.
2. Linear Dependence
A set of n – vectors. x1, x2, …….., xr is said to be linearly dependent if there exist scalars. k1, k2, ……., kr not all zero such that
k1 + x2k2 + …………….. + xr kr = 0 … (1)
3. Linear Independence
A set of r vectors x1, x2, …………., xr is said to be linearly independent if there exist scalars k1, k2, …………, kr all zero such that
x1 k1 + x2 k2 + …….. + xr kr = 0
Note:-
k1 = k2 = …….= kr = 0. Then the vector x1, x2, ……, xr are said to linearly independent.
4. Linear combination
A vector x can be written in the form.
x = x1 k1 + x2 k2 + ……….+xr kr
where k1, k2, ………….., kr are scalars, then X is called linear combination of x1, x2, ……, xr.
Results:
Example 1
Are the vectors 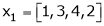 ,
, 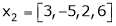 ,
,  linearly dependent. If so, express x1 as a linear combination of the others.
linearly dependent. If so, express x1 as a linear combination of the others.
Solution:
Consider a vector equation,
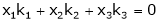
i.e. 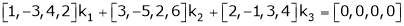
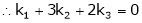
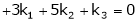
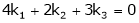
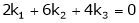
Which can be written in matrix form as,
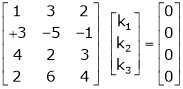

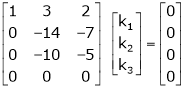
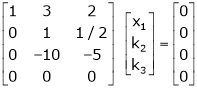
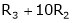
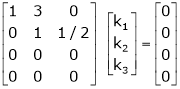
Here 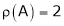 & no. of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,
& no. of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,
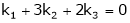
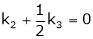
Put 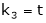
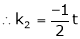 and
and
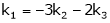

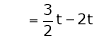
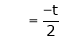
Thus 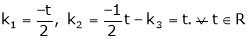
i.e. 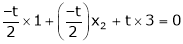
i.e. 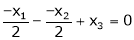
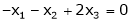

Since F11 k2, k3 not all zero. Hence  are linearly dependent.
are linearly dependent.
Example 2
Examine whether the following vectors are linearly independent or not.
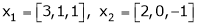 and
and 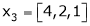 .
.
Solution:
Consider the vector equation,

i.e. 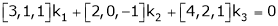 … (1)
… (1)
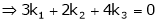
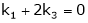
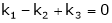
Which can be written in matrix form as,
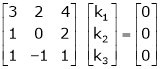
R12
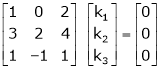
R2 – 3R1, R3 – R1
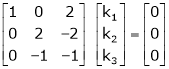
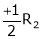

R3 + R2

Here Rank of the coefficient matrix is equal to the no. of unknowns. i.e. r = n = 3.
Hence the system has a unique trivial solution.
i.e. 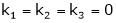
i.e. vector equation (1) has an only trivial solution. Hence the given vectors x1, x2, x3 are linearly independent.
Example 3
At what value of P the following vectors are linearly independent.
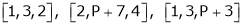
Solution:
Consider the vector equation.
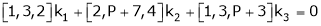
i.e.
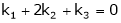
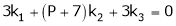
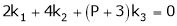
Which is a homogeneous system of three equations in 3 unknowns and has a unique trivial solution.
If and only if Determinant of the coefficient matrix is non zero.
 consider
consider  .
.
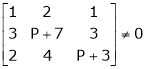 .
.
i.e.
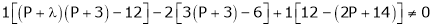
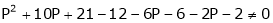
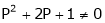
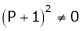
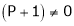
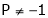
Thus for 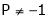 the system has an only trivial solution and Hence the vectors are linearly independent.
the system has an only trivial solution and Hence the vectors are linearly independent.
Note:-
If the rank of the coefficient matrix is r, it contains r linearly independent variables & the remaining vectors (if any) can be expressed as a linear combination of these vectors.
Eigenvector:-
Suppose 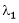 be an eigenvalue of a matrix A. Then
be an eigenvalue of a matrix A. Then  a non – zero vector x1 such that.
a non – zero vector x1 such that.
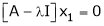 … (1)
… (1)
Such a vector ‘x1’ is called as eigenvector corresponding to the eigenvalue 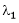 .
.
Properties of Eigenvalues:-

Properties of eigenvector:-
Example 1
Determine the eigenvalues of the eigenvector of the matrix.
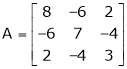
Solution:
Consider the characteristic equation as 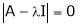
i.e. 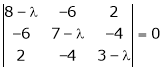
i.e. 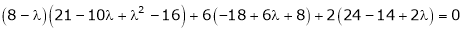
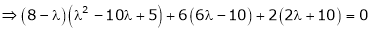
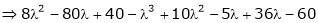
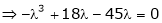
i.e. 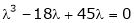
which is the required characteristic equation.
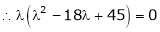
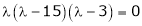
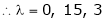 are the required eigenvalues.
are the required eigenvalues.
Now consider the equation
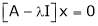 … (1)
… (1)
Case I:
If 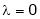 Equation (1) becomes
Equation (1) becomes
R1 + R2

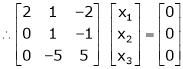

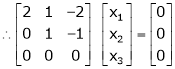
Thus 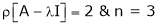
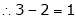 independent variable.
independent variable.
Now rewrite the equation as,
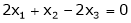
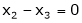
Put x3 = t
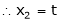 &
&
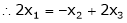
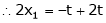
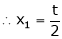
Thus 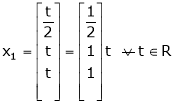 .
.
Is the eigenvector corresponding to 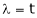 .
.
Case II:
If 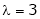 equation (1) becomes,
equation (1) becomes,
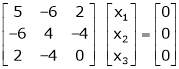
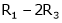
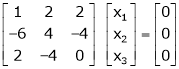
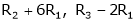
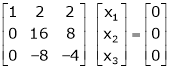
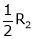
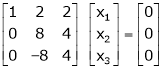
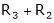

Here 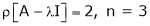
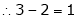 independent variables
independent variables
Now rewrite the equations as,
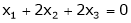

Put 
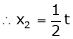 &
&
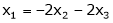
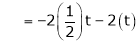

 .
.
Is the eigenvector corresponding to  .
.
Case III:
If 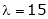 equation (1) becomes,
equation (1) becomes,
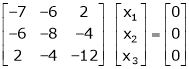
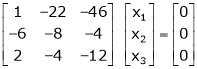
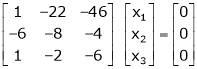
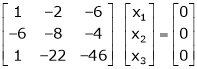
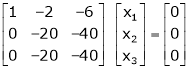

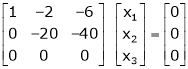
Here the rank of 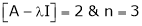
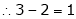 independent variable.
independent variable.
Now rewrite the equations as,
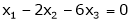
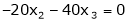
Put 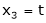
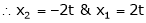
Thus 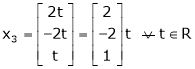 .
.
Is the eigenvector for 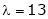 .
.
Example 2
Find the eigenvalues of an eigenvector for the matrix.
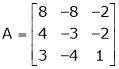
Solution:
Consider the characteristic equation as 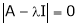
i.e. 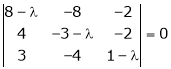

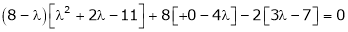
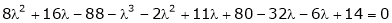
i.e. 
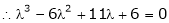
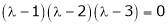
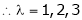 are the required eigenvalues.
are the required eigenvalues.
Now consider the equation
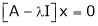 … (1)
… (1)
Case I:
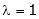 Equation (1) becomes,
Equation (1) becomes,
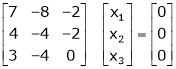
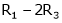
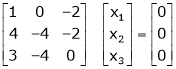
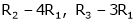
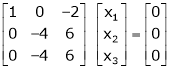
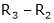

Thus 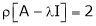 and n = 3
and n = 3
 3 – 2 = 1 independent variables.
3 – 2 = 1 independent variables.
Now rewrite the equations as,
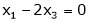
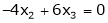
Put 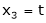
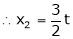 ,
, 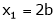

i.e. the eigenvector for 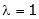
Case II:
If 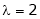 equation (1) becomes,
equation (1) becomes,
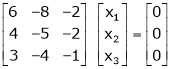
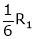
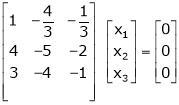
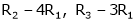
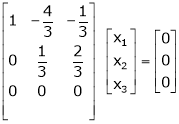
Thus 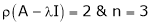
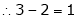
Independent variables.
Now rewrite the equations as,

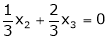
Put 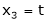

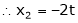
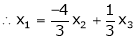
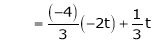
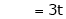
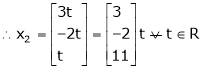
Is the eigenvector for 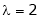
Now
Case II:-
If 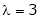 equation (1) gives,
equation (1) gives,

R1 – R2
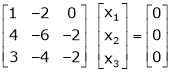
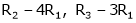
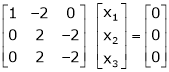

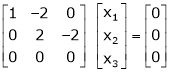
Thus 
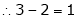 independent variables
independent variables
Now 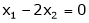
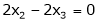
Put 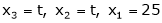
Thus
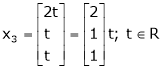
Is the eigenvector for 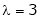 .
.

Elements are present in the diagonal of the matrix.
Reference Books-
1.E. Kreyszig, Advanced Engineering Mathematics, John Wiley & Sons, 2005.
2.Peter V. O’Neil, Advanced Engineering Mathematics, Thomson (Cengage) Learning, 2007.
3.Maurice D. Weir, Joel Hass, Frank R. Giordano, Thomas, Calculus, Eleventh Edition, Pearson.
4.D. Poole, Linear Algebra: A Modern Introduction, 2nd Edition, Brooks/Cole, 2005.
5.Veerarajan T., Engineering Mathematics for the first year, Tata McGraw-Hill, New Delhi, 2008.
6.Ray Wylie C and Louis C Barret, Advanced Engineering Mathematics, Tata Mc-Graw-Hill, Sixth Edition.
7.P. Sivaramakrishna Das and C. Vijayakumari, Engineering Mathematics, 1st Edition, Pearson India Education Services Pvt. Ltd
8. Advanced Engineering Mathematics. Chandrika Prasad, Reena Garg, 2018.
9. Engineering Mathematics – I. Reena Garg, 2018.